基于光纖法布里—珀羅腔的振動測量技術研究

蒲金飛, 蒲俊吉, 吳宇列, 肖定邦, 吳學忠

(國防科技大學 智能科學學院,湖南 長沙 410073)

0 引 言

近年來,隨著我國在基礎設施建設、大型工程設備及裝備等領域不斷取得跨越式發展,高精度及可靠性良好需求下的工程設備的故障診斷技術受到了研究人員們的廣泛關注。由于設備的振動信息所包含的工況內容最豐富,對于振動噪聲的監測抑制往往制約著裝備的穩定性及可靠性。特別是在航空航天領域內,由于航空發動機的原位振動嚴重影響航空器的壽命及安全可靠性,因此,如何實現高溫工作環境下(500～700 ℃)航空發動機內部狹小空間振動信號的高精度測量具有重要的工程意義[1]。

目前最常見的振動傳感器通常采用壓電式原理,盡管其靈敏度和信噪比較高,但容易受到外部電磁環境干擾,且振動傳感器大部分都是依賴進口[2],國產傳感器在溫度范圍和測量精度等方面有較大差距[3]。基于法布里—珀羅腔的測量技術是一種高精度的光學干涉測量技術,具有結構簡單、體積小、分辨率高、精度高等特點[4,5],近年來在振動測量中逐步得到研究。由于光纖具有耐高溫,且抗干擾能力強的特點,在高溫振動測量中也開始得到應用[6,7],但是目前光纖高溫振動測量技術并不成熟。

本文構建了一種面向高溫振動測量的光纖法布里—珀羅腔的振動測量系統,對其測量性能進行了深入研究,為構建應用于航空發動機的耐高溫小體積的振動測量傳感器提供了較好的技術基礎。

1 光纖法布里—珀羅腔干涉測量的基本原理

1.1 光纖法布里—珀羅腔干涉測量原理

標準法布里—珀羅腔結構利用多反射光線將在上平板處發生反射光線干涉現象,反射光譜可表示為式(1)[8]

(1)

(2)

式中R1和R2分別為上平板和下平板反射率,φ為相鄰反射光束相位差,n為腔體內介質的折射率。為表征法布里—珀羅腔反射光譜特性,引入用于表征法布里—珀羅腔可以分辨的最大波長差的參數Δλ

(3)

式中λ1和λ2分別為反射光譜中相鄰兩個波峰或波谷的波長。有別于標準法布里—珀羅腔結構,基于光纖傳播的法布里—珀羅腔由光纖出射端表面與振動器件反射面組成,如圖1(a)所示,由于光纖端部出射光束相較于準直光束發散角較大,僅有部分光束將反射進光纖內部,基于光纖傳播的法布里—珀羅腔反射光譜可簡化為雙光束干涉模型,即式(4)

(4)

式中η為反射光耦合進入光纖的效率。由于耦合效率η受到包括腔長、光纖參數等多重影響,這里并不作理論分析,僅給出典型光纖法布里—珀羅腔反射譜隨腔長變化的仿真特性曲線,如圖1(b)所示,從中可以看出,隨著腔長的增加反射率先減小后增加并最終維持一個穩定值[9]。

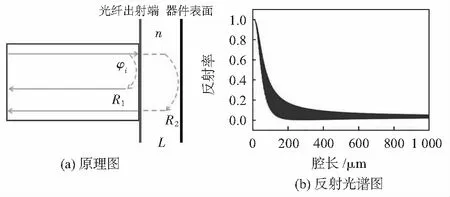
圖1 光纖法布里—珀羅腔干涉測量原理

引入雙光束干涉條紋對比度I表征干涉光譜特性

(5)

式中Rmax和Rmin分別為反射光譜相鄰波峰谷的反射率,對比度隨腔長的增加先增大后減小,其中在某一特定腔長處達到最大值1。

1.2 強度解調原理

為表征設備振動狀態下,腔長變化所引起的反射率的變化,定義法布里—珀羅腔傳感器的靈敏度為S,針對式(4)中的雙光束干涉模型,可得[10]

(6)

式中L0為法布里—珀羅腔初始長度。若想確保傳感器具有最大的靈敏度,則應保證sin(4πnL0/λ) =±1,即L0=(2m+1)λ/8n,m= 1,2,3...,此時

(7)

(8)

從式(5)和式(8)中可以發現,光纖法布里—珀羅腔靈敏度正比于反射光譜對比度,因此,對比度取最大時的腔長即為最優腔長,傳感器此時處于最大靈敏度。

2 基于光纖法布里—珀羅的振動測量系統

搭建如圖2所示的法布里—珀羅腔振動測量系統,其中包括可調諧激光模塊、光反射模塊、數據采集及分析模塊等。1)可調諧激光模塊：包括窄線寬調諧激光器,可形成中心波長1 550 nm,光譜覆蓋范圍為(1 550±10)nm的準直激光。2)光反射模塊：包括光循環器、耦合器、單模光纖。可調諧激光器出射光耦合進入光循環器及單模光纖,并從光纖出射端垂直照射至振動器件,反射光以反向光路再次耦合進光循環器和耦合器。3)數據采集及分析模塊：包括光功率計、光電探測器、數據采集卡、計算機。反射光由耦合器分光,一路功率計接收,實現反射光譜的實時檢測；另一路由光電探測器接收并通過數據采集卡及計算機進行后處理。

圖2 法布里—珀羅腔振動傳感系統實物

3 工作點穩定性能研究

為了實現腔長變化與反射光強變化具有最大的線性區間,應保證傳感器工作點位于線性區間的中心點,此時工作點對應的反射光強為中值光強,該點稱為正交工作點(Q點)。由于傳感器正常工作條件不僅受限于傳感器自身性能及結構屬性,還受到外界環境的影響,例如隨外界環境振動而產生的腔長漂移,這使得傳感器無法確保始終處于靈敏度最高的正交工作點。因此,必須引入反饋控制從而確保傳感器的工作性能。

工作點的反饋控制主要包括兩個步驟,首先，是確定正交工作點,利用可調諧激光器進行波長掃描從而確定掃描結果中的最大光強和最小光強,通過兩點對應的波長計算出傳感器最佳工作波長,最后控制激光器總是工作在該波長處。其次,當腔長漂移時光反射譜會發生實時變化,并使得最初確定的工作點發生改變,而這種漂移往往只會造成反射譜的相位變化,如圖3所示,這就需要將原有工作點平移一個相位變化量并達到新的工作位置。

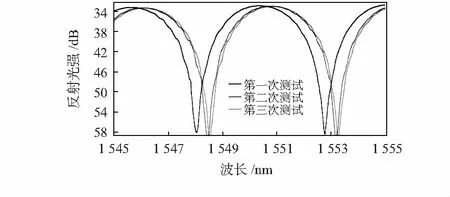
圖3 反射譜隨時間變化而發生相位漂移

如圖4所示為Q點反饋控制的原理圖,其中，曲線I1為t時刻的反射光譜,I2為t+Δt時刻的反射光譜。假定漂移不會造成光強的變化,則I2相對I1橫向偏移Δλ的相位。

假設t+Δt時刻探測的激光波長為λ2c,光強為Ic,可以根據t時刻的原始數據計算當前光強下原始反射光譜所對應的波長λ1c,此時就可以計算出波長漂移量

Δλ=λ2c-λ1c

(9)

此時t+Δt時刻的Q點波長即為

λ2Q=λ1Q+Δλ=λ1Q+λ2c-λ1c

(10)

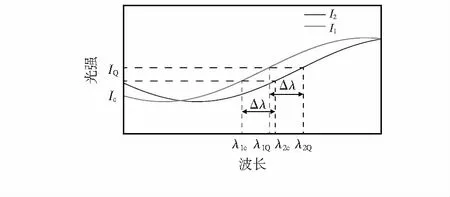
圖4 Q點反饋控制原理

對傳感器進行工作穩定性測試實驗。在完成初次反射譜掃描后確定傳感器Q點所對應的最佳波長,并將可調諧激光器的輸出波長設置為Q點波長,利用光電探測器首先測試無外部反饋控制的光強信號,如圖5(a)所示。可以看出在腔長固定的情況下反射光強仍然發生了明顯的漂移,而在引入式(10)的控制算法后,利用比例控制對于反射光強進行了明顯改善,其中信號毛刺來源于切換波長過程帶來的噪聲。

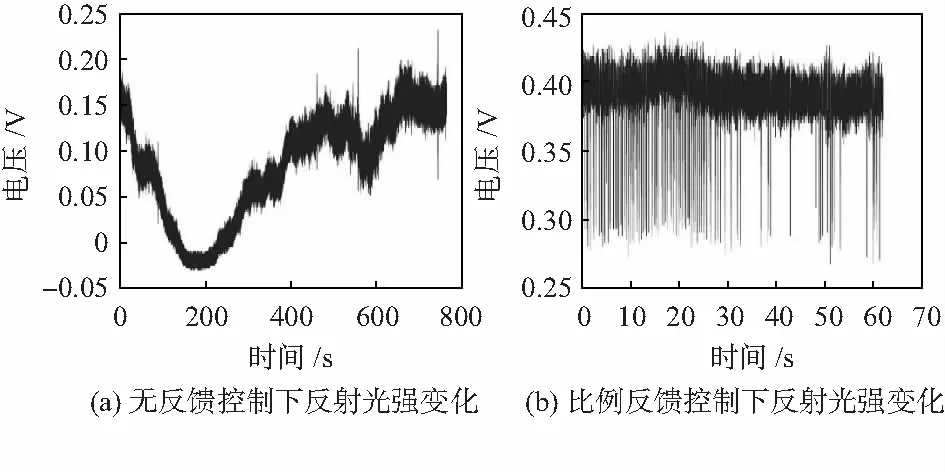
圖5 Q點穩定性測試

4 高頻率振動測量

采用陶瓷壓電片作為振動器件,首先利用激光測振儀系統配合鎖相放大器實現對壓電片的掃頻分析,從而確定其振動頻率及幅值。之后利用光纖法布里—珀羅腔振動測量系統對高頻驅動下壓電片的振動信號進行測試,從而驗證該系統對于高頻率振動的響應性能。

通過鎖相放大器可以得到陶瓷壓電片的多個諧振頻率,為實現光纖測量系統對于高頻振動的測量,選取40 kHz 的諧振頻率作為驅動頻率。在完成對光纖法布里—珀羅腔在Q點的反饋控制后,通過信號發生器激振陶瓷壓電片,其頻域信號如圖6(a)所示,當壓電片開始激振時該系統存在明顯的響應信號,通過分析功率譜可以看到頻率為40 kHz時存在明顯的諧振峰值,這表明測量系統可以實現高頻振動的測量。但通過增大激振電壓并不能改變功率譜的諧振峰值,這是因為壓電片的振動幅值已經超過了激光波長的1/4即該系統的線性工作區間,信號處于飽和狀態。

圖6 利用光纖系統進行陶瓷壓電片的頻譜分析

5 小振動測量

5.1 激光測振儀系統小振動測試

作為法布里—珀羅腔振動傳感系統的對照標定,首先利用激光測振儀系統對周期振動的杯型陀螺儀進行信號測試。選取杯型陀螺儀內圈為測試點,驅動頻率為一階模態振動頻率,如圖7(a),驅動電壓分別為1,5,10,50,100 mV從而得到陀螺振動幅值—驅動電壓擬合曲線,如圖7(b)。不難發現,工作在諧振頻率下陀螺的振動幅值與驅動電壓存在明顯的線性關系。

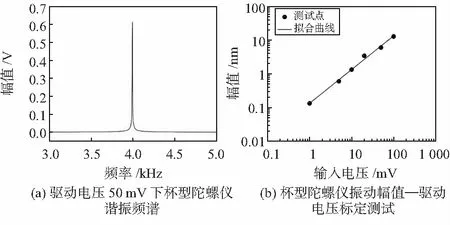
圖7 激光測振儀系統小振動測試

5.2 法布里—珀羅腔振動測量系統小振動測試與標定

為獲得較大靈敏度,選取反射譜消光比約20 dB所對應的腔長為最佳腔長。采用5.1節所述驅動電壓得到測量數據并計算出測定數據的功率譜密度,如圖8(a),由此得到標定曲線如圖8(b)。

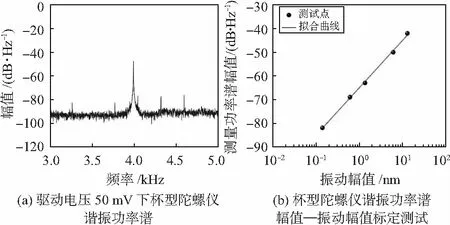
圖8 法布里—珀羅腔振動傳感系統小振動測試

實驗結果表明,法布里—珀羅腔振動傳感系統實現了對杯型陀螺儀振動信號的測試并表達了很好的線性關系,由于其功率譜本底噪聲為-90 dB可知,系統可以實現最高精度0.05 nm的振動信號測量。

6 結 論

本文首先從理論上分析了光纖法布里—珀羅腔結構的振動傳感系統測試原理,其次根據測試機理搭建了光纖法布里—珀羅腔振動傳感系統。分別開展了工作點穩定性能研究、高頻率振動測量和小振動測量研究。結果表明:利用比例反饋控制算法實現了對反射譜相位漂移的抑制,并實現了對40 kHz高頻振動的壓電片及0.05 nm小幅振動的杯型陀螺儀的測試,這對于未來高溫條件下航空發動機內振動信號高精度測量及診斷抑制具有重要意義。在后續工作中可以進一步抑制環境及激光本體噪聲,提高法布里—珀羅腔振動傳感系統的測量精度并拓展其工程應用范圍。