溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板的自由振動分析

滕兆春，王偉斌，鄭文達

(蘭州理工大學理學院，蘭州 730050)

功能梯度材料(functionally graded materials，FGM)具有材料性能平滑、連續變化的特點，在世界范圍內得到了迅速的研究、開發和應用[1]，FGM矩形板被廣泛應用于土木、機械和海洋工程等[2]。隨著新型材料的興起，FGM板結構具有常見復合材料板難以比擬的優點。關于FGM常見結構的力學行為研究已有較多文獻成果，如Wattanasakulpong等[3]采用微分變換法(differential transformation method，DTM)研究了FGM階梯梁的自由振動，得到了梁的固有頻率和振型。Roshan等[4]在經典平板理論的基礎上，對面內均布力作用下的FGM圓板振動問題進行了分析和數值計算，研究了梯度指數和面內力對前三階振動固有頻率的影響。Ghazaryan等[5]利用DTM對非均勻截面軸向功能梯度Euler-Bernoulli梁的自由振動進行了分析，并驗證了該方法可用于軸向材料非均勻或者幾何非均勻的各種類型梁的計算。Shishesaz等[6]基于應變梯度理論，研究了FGM納米圓盤的熱彈性行為，主要分析了溫度變化對納米圓盤應力和徑向位移的影響。Abdolhossein等[7]考慮流體-結構相互作用研究了彈性地基上部分充液FGM圓柱殼在熱環境下的自由振動問題。Ladislav等[8]基于經典彈性理論研究了FGM薄板在熱載荷作用下的彎曲問題，結合移動最小二乘逼近的數值方法，重點研究了材料相關參數對板撓度的影響。Saini等[9]基于經典板理論，考慮材料溫度依賴性質，分析了熱環境中FGM圓板在均勻面內軸向載荷和沿厚度方向的非線性溫度分布作用下軸對稱屈曲和振動問題。Chakraverty等[10]基于基爾霍夫板理論，利用Rayleigh-Ritz法研究了FGM矩形板的自由振動問題。蔣偉男等[11]基于三階剪切理論提出考慮橫向拉伸影響的位移場，研究了具有簡支和固支邊界條件下的FGM矩形夾層板的自由振動。何昊南等[12]基于幾何非線性和物理中面，分析了熱對材料參數影響下FGM梁的熱后屈曲特性。當然，上述研究工作大多是從材料的理想形態入手建立力學模型并進行分析，忽略了FGM在實際應用中孔隙的存在。

FGM在各領域的廣泛需求，促進了其制備技術的快速發展，各種FGM制備方法先后出現。但由于現有某些制備技術的缺陷，制備過程中在FGM內部不可避免的會出現小的孔隙，則形成多孔FGM。同時，隨著FGM越來越多的應用擴展，也可以使用陶瓷和泡沫金屬來制備多孔FGM形成工程中可應用的一些特殊功能結構，如過濾器、催化器、燃燒室和生物材料等。這些孔隙對FGM的物理性能、功能使用和靜動力特性有著較大的影響，因此越來越多的科研人員開始關注多孔FGM結構的力學行為研究。Behravan等[13]基于微分求積和狀態空間矢量技術的求解方法，對彈性地基非均勻面力作用下非對稱變厚度多孔FGM圓板的三維磁彈性特性進行了分析。Aria等[14]首次提出了一種有限元模型，基于冪律形式分析了多孔FGM納米梁的熱彈性行為。蒲育等[15?17]基于一種擴展的廣義梁理論，分別采用廣義微分求積法和萊維法，考慮材料性質隨溫度的相關性，研究了熱環境中軸向機械力作用含均勻孔隙FGM梁的耦合振動和耦合屈曲特性以及濕-熱-機-彈耦合作用下多孔FGM梁的振動和屈曲特性。蘇盛開等[18]采用Euler梁理論和高階三角剪切變形理論研究了多孔FGM梁的熱力耦合屈曲行為。Ebrahimi等[19]利用DTM對轉動多孔FGM Timoshenko梁進行橫向振動分析，并在修正混合率公式的基礎上研究了孔隙率、梯度指數、轉速等參數對轉動多孔FGM梁無量綱固有頻率的影響。綜上所述，已有文獻中大多學者基本都專注于多孔FGM梁的研究，對多孔FGM板的研究則相對較少，同時一些研究結果也很好地驗證了DTM的實用性和有效性。

目前關于溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板自由振動問題的研究在國內外還未見有文獻報道，且考慮到彈性地基板在工程中的廣泛應用背景，因此在參照文獻[20]的基礎上，本文將一種隨機均勻分布的孔隙引入力學模型，采用DTM對溫度影響下Winkler- Pasternak彈性地基上多孔FGM矩形板自由振動展開研究，分析梯度指數、孔隙率、升溫、地基剛度系數、邊界條件、長寬比和邊厚比等對多孔FGM矩形板無量綱固有頻率的影響，為今后多孔FGM板的研究提供數據支撐。

1 控制微分方程的建立

1.1 材料物性描述

如圖1所示：在三維笛卡爾坐標系中，溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板厚度為h， 長為a， 寬為b，xoy平面為板的幾何中面，kw和qw分別為Winkler-Pasternak地基的彈性剛度系數和剪切剛度系數。

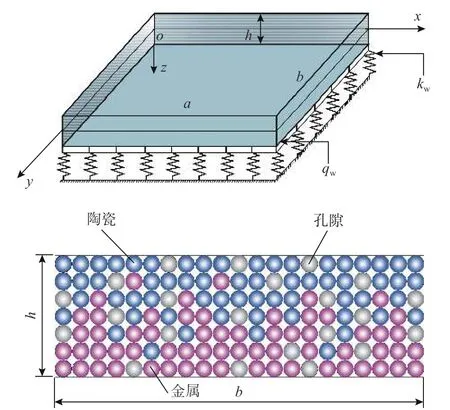
圖1 彈性地基上多孔FGM矩形板的幾何模型和截面上均勻分布的孔隙Fig.1 Geometric model of a porous FGM rectangular plate on elastic foundation and cross-section with evenly distributed porosity

考慮到 FGM 的物性參數與溫度T有關，采用Voigt混合冪律模型[21]。物性參數滿足：

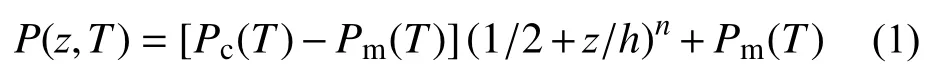
式中：P可表示彈性模量E、密度 ρ和熱膨脹系數α ；T為絕對溫度；n為 梯度指數；下標 c 和 m則分別為陶瓷和金屬材料的物性參數。

上述金屬和陶瓷的某一物性參數G隨溫度T的變化可采用 Touloukian 非線性函數，統一表述為[14]：

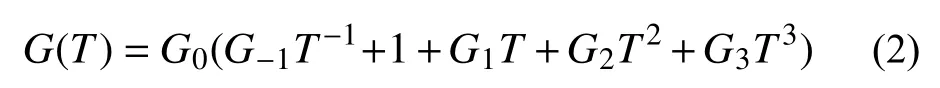
式 中，G0、G-1、G1、G2和G3為 溫 度 相 關 的 系數，一般由實驗給出，可見表1。

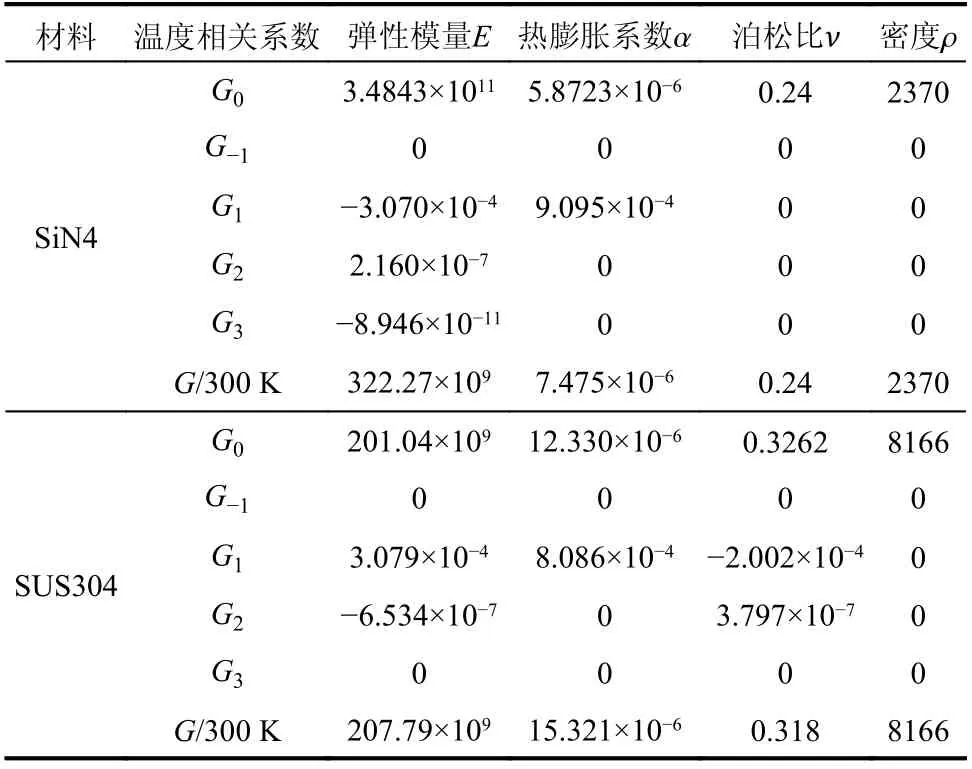
表1 陶瓷和金屬材料物性參數的溫度相關系數表[14]Table 1 Temperature correlation coefficient of physical parameters of ceramic and metal materials[14]

當FGM中存在孔隙時，可以假設孔隙的大小和分布是任意的，并且介質是連續致密的，在此基礎上得到了孔隙率 θ與彈性模量E、泊松比ν和密度 ρ的關系[20]。定義孔隙率如下：

式中： ρ(z) 為 致密密度； ρ0(z)為自然密度。

有效泊松比和有效彈性模量分別為：

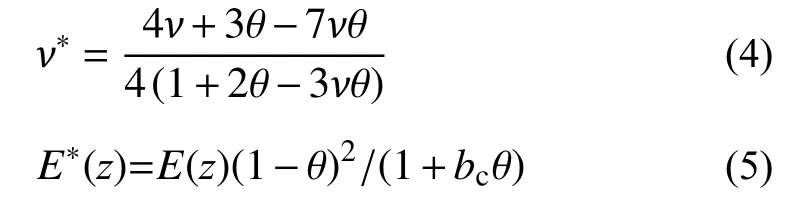
式中：ν、E(z) 和ν?、E?(z) 分 別為 θ=0 和 0<θ<1時的泊松比及彈性模量；bc=2-3ν。將式(1)～式(3)代入式(5)即可得到不同孔隙率下 FGM 矩形板的有效彈性模量。

1.2 Winkler-Pasternak地基模型和升溫

雙參數Winkler-Pasternak彈性地基中考慮了剪力的作用，地基-板相互作用力F和矩形板橫向位移w的關系為[22]：

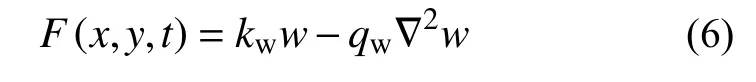
式中：kw、qw分別為地基的彈性剛度系數和剪切剛度系數； ?2為二維Laplace算子。

本文僅考慮均勻升溫：

式中：T0為無應力狀態的參考溫度，本文取T0=300 K； ΔT為升溫值。

1.3 基本方程

根據薄板和小撓度理論的基本假設，溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板位移場為：

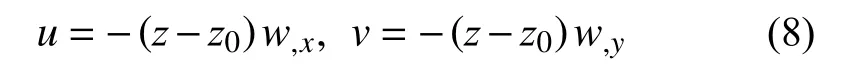
式中：u、v和w分 別為板內一點沿x、y和z方向的位移分量；z0為物理中面。物理中面內應力分量與應變分量均為零，其表達式如下[23]：

幾何方程為：

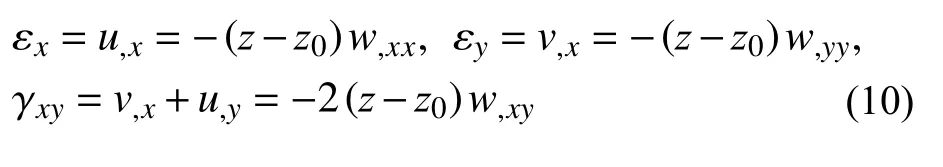
本構方程為：

下面應用Hamilton原理建立溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板的運動微分方程。已知哈密頓原理如下：

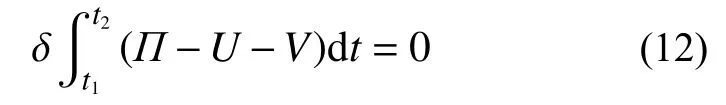
式中： Π 、U和V分別為地基-板系統的動能、應變能和外力勢能；δ為變分符號；t1和t2分別為系統運動的初始時刻和終止時刻。這里只考慮橫向位移，令w=w(x,y,t)，可得：

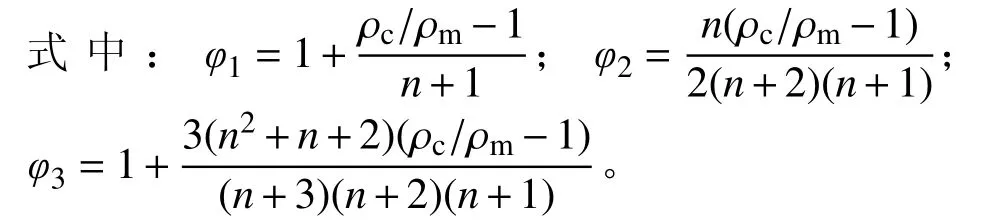
考慮溫度在板內均勻變化，且忽略面內和轉動慣性力，可得溫度影響下彈性地基上多孔FGM矩形板橫向運動的控制微分方程：

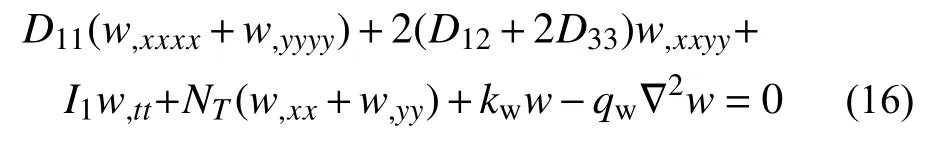
2 無量綱控制微分方程及DTM變換

2.1 無量綱控制微分方程

溫度影響下彈性地基上多孔FGM矩形板在y=0 和y=b處 為簡支(S)邊界，而在x=0 和x=a處可為固定(C)邊界、簡支(S)邊界或自由(F)邊界。在本文的問題討論中，邊界條件按照x=0、y=b、x=a和y=0的順序給出。

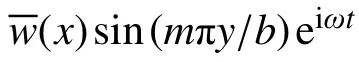
綜上可得到溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板自由振動時的無量綱控制微分方程：

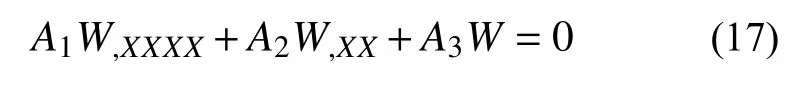
式中：

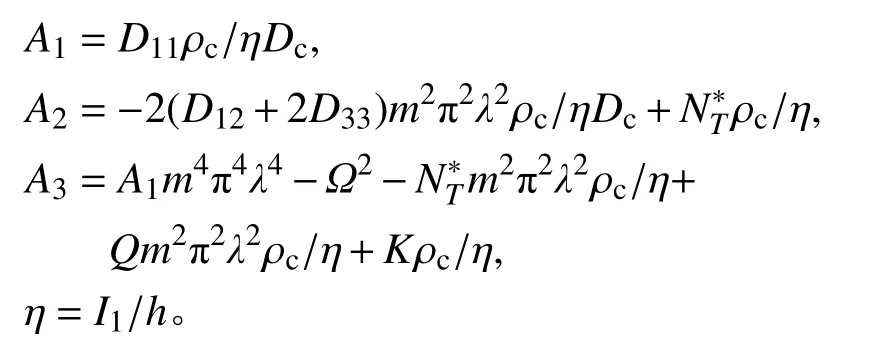
式中：A1、A2、A3分別為四階微分方程各項系數；η為慣性系數。

接下來考慮多孔 FGM 矩形板在X=0 和X=1處的無量綱邊界條件，其形式如下：

簡支(S)：

固定(C)：

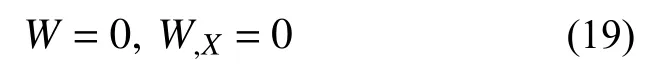
自由(F)：

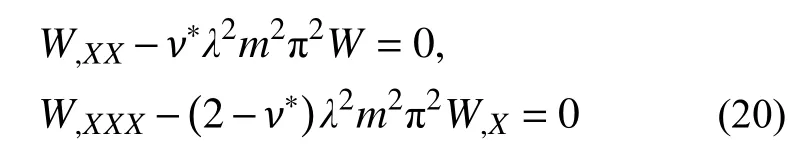
2.2 DTM變換

對于溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板自由振動的無量綱控制微分方程式(17)的求解，本文采用一種半解析法—微分變換法(DTM)[24]進行求解。按照DTM的求解過程及原理，將溫度影響下彈性地基上多孔FGM矩形板自由振動的無量綱控制微分方程轉換為如下的迭代代數方程：

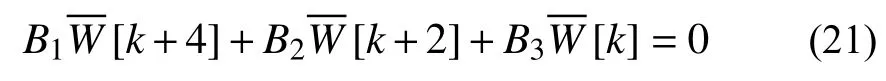
邊界條件的DTM變換如下：

在X=0處：

簡支(S)：

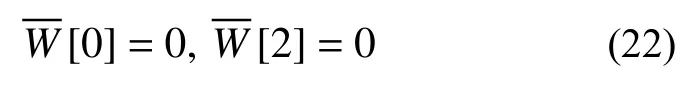
固定(C)：

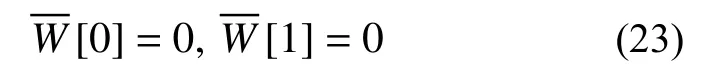
自由(F)：

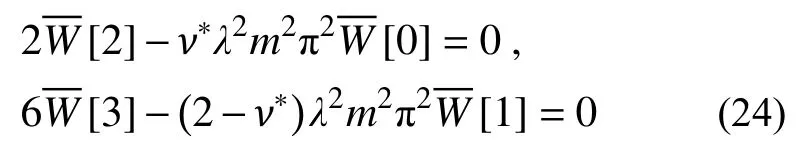
在X=1處：

簡支(S)：

固定(C)：

自由(F)：

結合式(21)～式(27)，邊界條件為兩邊固定兩邊簡支(CSCS)、一邊固定三邊簡支(CSSS)和一邊固支一邊自由兩對邊簡支(CSFS)的關于無量綱固有頻率的特征方程如下：

對于邊界條件為四邊簡支(SSSS)和一邊自由三邊簡支(SSFS)，關于無量綱固有頻率的特征方程如下：

要求得無量綱的固有頻率必須滿足：

對于邊界條件為兩邊自由兩邊簡支(FSFS)，關于無量綱固有頻率的特征方程如下：

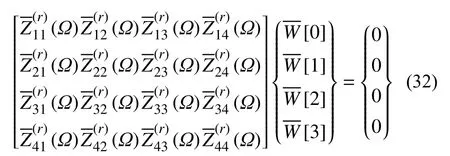
同理，必須滿足：

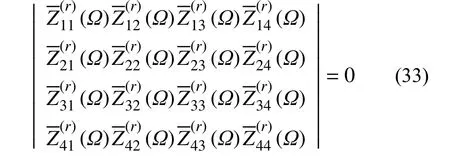
式中，γ為迭代誤差限，這里取 γ=0.000001。

3 計算結果及分析

應用MATLAB軟件編寫相關程序，由此可得到由DTM求解溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板自由振動時的無量綱固有頻率。為了驗證DTM的正確性，將溫度影響下彈性地基上多孔FGM矩形板，經算例1退化為孔隙率為零時的FGM矩形板和Winkler彈性地基上FGM矩形板，并與文獻[25]中的結果進行比較。經算例2得到新的結果。

算例1. 300 K下陶瓷和金屬的物性參數分別取為： ρc=3800kg/m3， ρm=2700kg/m3，Ec=380 GPa，Em=70 GPa。

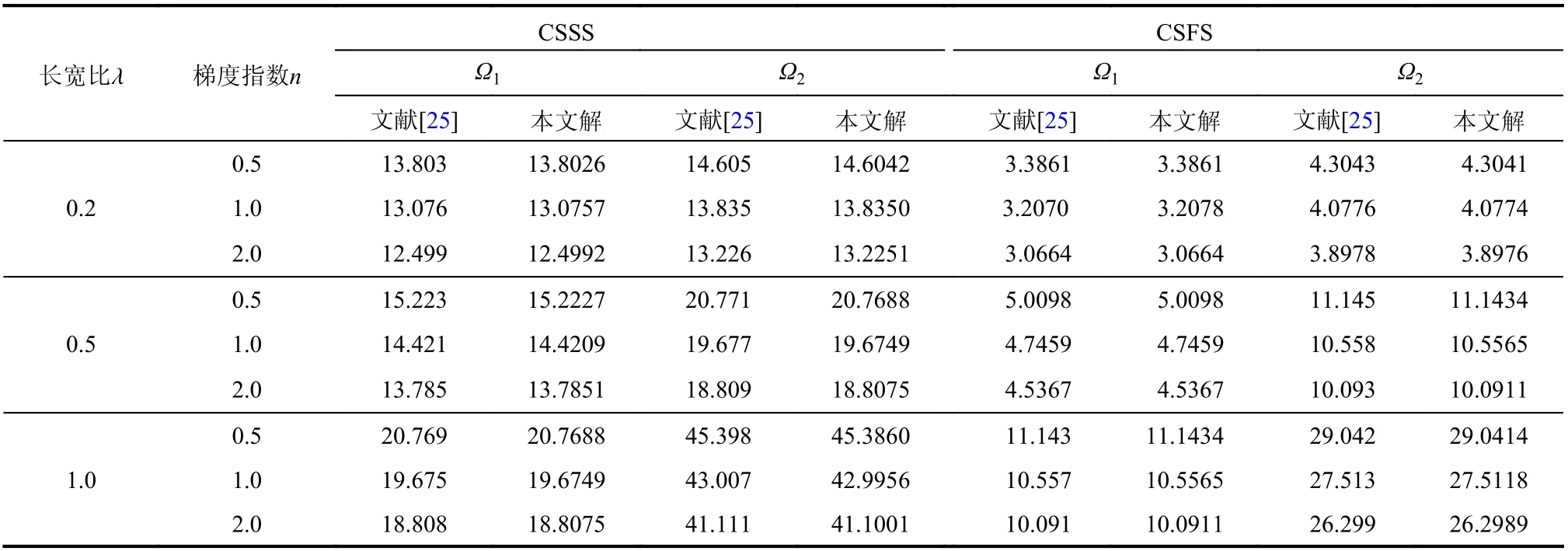
表2 CSSS和CSFS邊界條件下不同長寬比、不同梯度指數對FGM矩形板無量綱固有頻率的影響Table 2 Influence of aspect ratio and gradient index on dimensionless natural frequencies of FGM rectangular plate with CSSS and CSFS boundary conditions

表3 CSCS和SSSS邊界條件下長寬比對Winkler彈性地基上FGM矩形板無量綱固有頻率的影響(n=1, K=100)Table 3 Influence of aspect ratio on dimensionless natural frequencies of FGM rectangular plate on Winkler elastic foundation with CSCS and SSSS boundary conditions (n = 1, K = 100)

算例2. 圖2～圖6中各物性參數均遵循表1中的實驗數據，其中，泊松比ν取陶瓷材料和金屬材料的平均值即：ν=(νc+νm)/2=0.280。

圖2反映了當θ =0.2 ，H=0.1 ，λ=1 ，K=100，Q=10 ，ΔT=100K，在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下梯度指數n與前三階的無量綱固有頻率 Ω的關系曲線。結果顯示：隨著n的增大，無量綱固有頻率 Ω總體上在減小。當n在小值范圍取值時，無量綱固有頻率減小趨勢很劇烈；當n在較大值范圍取值時，無量綱固有頻率變化趨于平緩；當n的值一定時，邊界約束越強，無量綱固有頻率越大，即CSCS固有頻率>CSSS固有頻率>SSSS固有頻率>CSFS固有頻率>SSFS固有頻率>FSFS固有頻率。

圖2 不同邊界條件下梯度指數對Winkler-Pasternak彈性地基上多孔FGM矩形板無量綱固有頻率的影響Fig.2 Influence of gradient index on the dimensionless natural frequencies of porous FGM rectangular plates on Winkler-Pasternak elastic foundations under different boundary conditions

圖3給出當n=1 ，H=0.1 ，λ=1 ，K=100，Q=10 ， ΔT=100 K時，在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下孔隙率 θ與前三階無量綱固有頻率 Ω的關系。結果顯示：一階無量綱固有頻率在CSCS、CSSS、SSSS邊界下隨著孔隙率的增大而減小，在CSFS、SSFS和FSFS邊界下，一階無量綱固有頻率起初隨孔隙率增大而減小，后又微弱增大趨勢。而二階、三階無量綱固有頻率隨著孔隙率的增大在減小，且減小的幅度比一階要大。當 θ一定時，邊界約束越強，無量綱固有頻率越大，即CSCS固有頻率>CSSS固有頻率>SSSS固有頻率>CSFS固有頻率>SSFS固有頻率>FSFS固有頻率。

圖3 不同邊界條件下孔隙率對Winkler-Pasternak彈性地基上多孔FGM矩形板無量綱固有頻率的影響Fig.3 Influence of porosity on the dimensionless natural frequency of porous FGM rectangular plate on Winkler-Pasternak elastic foundation under different boundary conditions

圖4給出當n=1 ，H=0.1 ，λ=1 ，K=100，θ=0.2 ，Q=10時，在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下溫升ΔT與前三階無量綱固有頻率 Ω的關系。結果顯示：前三階無量綱固有頻率隨著溫升的不斷增大而減小，且二階和三階無量綱固有頻率減小的幅度比一階大。

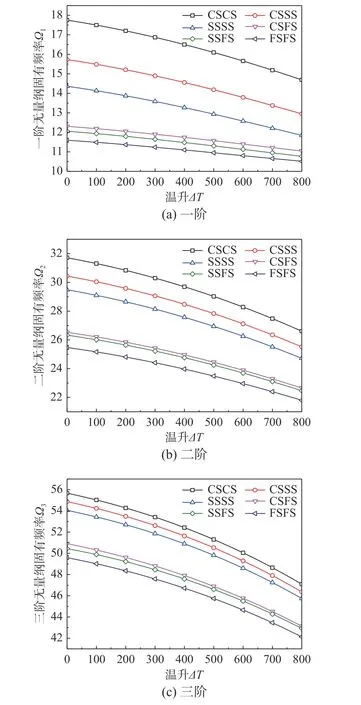
圖4 不同邊界條件下溫升對Winkler-Pasternak彈性地基上多孔FGM矩形板無量綱固有頻率的影響Fig.4 Influence of temperature rise on the dimensionless natural frequency of porous FGM rectangular plate on Winkler-Pasternak elastic foundation under different boundary conditions

圖5為n=1 ，H=0.1 ，ΔT=100 K，K=100，θ=0.2 ，Q=10時，在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下長寬比λ與前兩階無量綱固有頻率 Ω的關系。結果顯示：前兩階無量綱固有頻率隨著長寬比的增大而增大，且二階無量綱固有頻率增大的幅度比一階大。當長寬比λ一定時，邊界約束越強，無量綱固有頻率越大，即CSCS固有頻率>CSSS固有頻率>SSSS固有頻率>CSFS固有頻率>SSFS固有頻率>FSFS固有頻率。

圖5 不同邊界條件下長寬比對Winkler-Pasternak彈性地基上多孔FGM矩形板無量綱固有頻率的影響Fig.5 Influence of the aspect ratio on the dimensionless natural frequency of the porous FGM rectangular plate on the Winkler-Pasternak elastic foundation under different boundary conditions

圖6 給出了在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下，當n=1 ，H=0.1 ， ΔT=100 K，λ=1 ， θ=0.2 ，Q=10無量綱彈性剛度系數K對無量綱固有頻率 Ω的影響。結果表明：前兩階無量綱固有頻率隨著無量綱剛度系數的增大而增大，且二階無量綱固有頻率幾乎呈線性變化，當無量綱彈性剛度系數K一定時，邊界約束越強，無量綱固有頻率越大, 即CSCS固有頻率>CSSS固有頻率>SSSS固有頻率>CSFS固有頻率> SSFS固有頻率>FSFS固有頻率。

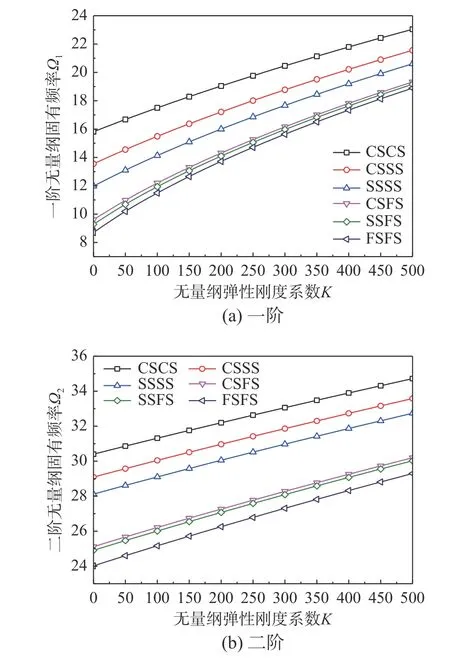
圖6 不同邊界條件下無量綱彈性剛度系數對Winkler-Pasternak彈性地基上多孔FGM矩形板無量綱固有頻率的影響Fig.6 Influence of dimensionless elastic stiffness coefficient on the dimensionless natural frequencies of porous FGM rectangular plate on Winkler-Pasternak elastic foundation with different boundary conditions

圖7 反映了在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下，當n=1 ，H=0.1 ， ΔT=100 K，λ=1 ， θ=0.2 ，K=100，無量綱剪切剛度系數Q對無量綱固有頻率 Ω的影響，結果表明：前兩階無量綱固有頻率隨著無量綱剛度系數Q的增大而增大。且二階無量綱固有頻率比一階無量綱固有頻率增大得到幅度大，當Q的值一定時，邊界約束越強，無量綱固有頻率越大，即CSCS固有頻率>CSSS固有頻率>SSSS固有頻率>CSFS固有頻率> SSFS固有頻率>FSFS固有頻率。

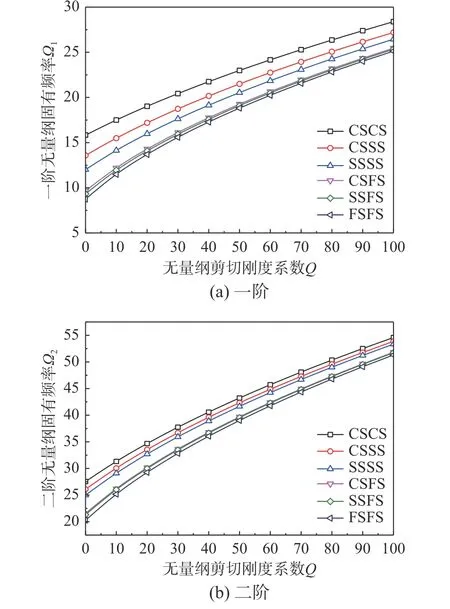
圖7 不同邊界條件下無量綱剪切剛度系數對Winkler-Pasternak彈性地基上多孔FGM矩形板無量綱固有頻率的影響無量綱固有頻率的影響Fig.7 Influence of dimensionless shear stiffness coefficient on the dimensionless natural frequencies of porous FGM rectangular plate on Winkler-Pasternak elastic foundation with different boundary conditions

圖8 給出了在CSCS、CSSS、SSSS、CSFS、SSFS和FSFS邊界條件下，當n=1 ， ΔT=100K ，λ=1 ， θ=0.2 ，K=100 ，Q=10 ， 邊 厚 比 1/H對一階無量綱固有頻率 Ω1(即無量綱基頻)的影響。這里邊厚比的取值為8～60之間，結果表明：一階無量綱固有頻率均隨著邊厚比 1/H的增大而減小。由于隨著邊厚比的增大，多孔FGM矩形板的整體剛度趨向于減小，從而導致這一必然結果。

圖8 不同邊界條件下邊厚比對Winkler-Pasternak彈性地基上多孔FGM矩形板一階無量綱固有頻率的影響Fig.8 Influence of side-to-thickness ratio on first dimensionless natural frequencies of porous FGM rectangular plate on Winkler-Pasternak elastic foundation with different boundary conditions

4 結論

本文基于Hamilton原理和經典薄板理論建立了溫度影響下Winkler-Pasternak彈性地基上多孔FGM矩形板自由振動的控制微分方程并無量綱化，然后運用微分變換法(DTM)對無量綱控制微分方程及其邊界條件進行變換，通過編寫MATLAB程序求解出無量綱固有頻率，并分別給出了不同參數值的變化對無量綱固有頻率的影響。得到主要結論如下：

(1) 多孔FGM矩形板無量綱固有頻率 Ω 隨著梯度指數n的增大而減小，隨著梯度指數n趨向于無窮大，無量綱固有頻率趨于不變，合理的解釋了FGM中陶瓷材料向金屬材料過渡的特性。

(2) 多孔FGM矩形板無量綱固有頻率 Ω隨著孔隙率 θ變化：一階無量綱固有頻率在CSCS、CSSS、SSSS邊界下隨著孔隙率的增大而減小，在CSFS、SSFS和FSFS邊界下，一階無量綱固有頻率起初隨孔隙率增大而減小，后有微弱增大趨勢。而二階、三階無量綱固有頻率隨著孔隙率的增大在減小，且減小的幅度比一階要大。

(3) 多孔FGM矩形板前三階無量綱固有頻率Ω隨著溫升ΔT的增大而減小，且二階和三階無量綱固有頻率減小的幅度比一階大。

(4) 多孔FGM矩形板無量綱固有頻率 Ω隨著無量綱彈性剛度系數K的增大而增大，且二階無量綱固有頻率幾乎呈線性變化。隨著無量綱剪切剛度系數Q的增大而增大。

(5) 多孔FGM矩形板前兩階無量綱固有頻率隨著長寬比的增大而增大。一階無量綱固有頻率Ω隨著邊厚比 1/H的增大而減小。