考慮粘滑效應的核電站環行起重機地震瞬態響應分析

張欣剛，王海明，姚文莉，齊朝暉，何 穎

(1. 青島理工大學理學院，青島 266525；2. 大連理工大學工程力學系，大連 116024；3. 大連科技學院交通運輸學院，大連 116052)

核電站環行起重機(簡稱核環吊，如圖1所示)運行于核島安全殼上方，下方安裝有反應堆堆芯、蒸汽發生器等核島關鍵設施，其抗震性能是影響核安全的重要因素[1 ? 2]。按照規范要求[3]，地震發生時整機應維持在既定位置上，部件和載荷不跌落，地震過后經過整修能夠繼續投入使用。達到上述高性能要求，導行裝置的制動、隔震性能是關鍵。因此，在進行縮比實驗之前，提煉出合理的動力學模型，準確的反映輪軌之間的接觸、摩擦特征，可為后續實驗的開展提供理論牽引，并為實驗方案的優化提供前期的數據儲備。

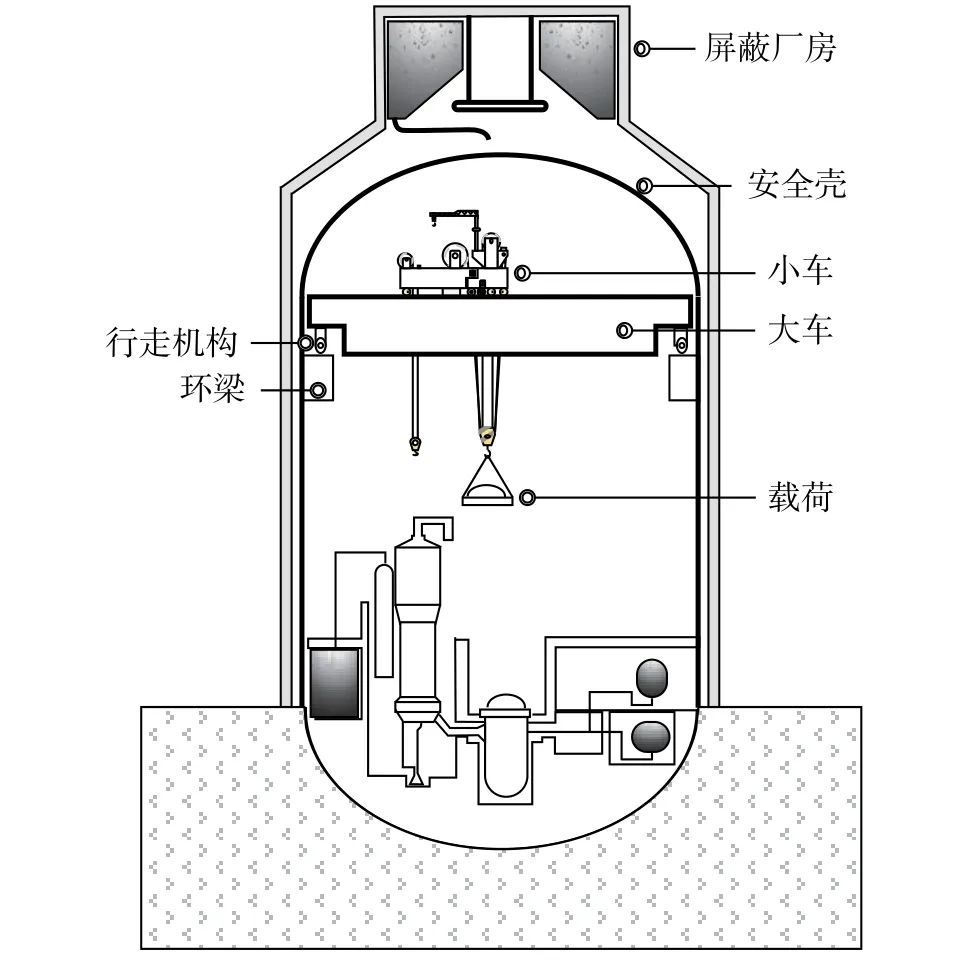
圖1 核島示意圖Fig.1 Nuclear island diagram

目前，結構抗震分析受到了廣泛的研究[4 ? 6]，但針對機構抗震進行的分析還較少。針對核環吊地震響應進行的研究往往以環吊本體為研究對象，采用反應譜法等準靜態方法為分析手段，以樓層譜[7 ? 8]為計算依據，難以考慮輪軌之間的瞬態作用。對于隔振裝置，通常采用單向受壓的桿單元進行簡化，無法準確反映強震階段水平方向上瞬時沖擊的細節，難以適應我國三代核環吊的發展要求。

除若干瞬時跳軌時刻外，核環吊各行走機構處于緊密貼合狀態，但部件在水平強震作用下易發生瞬時滑移。目前機械系統動力學常采用修正的庫侖摩擦模型反映摩擦效應[9 ? 10]，例如：

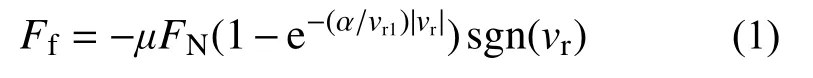
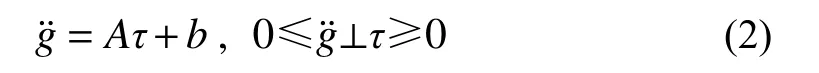
可通過成熟的互補理論進行求解，也可將其改寫為一組等價的非線性方程組[13]：

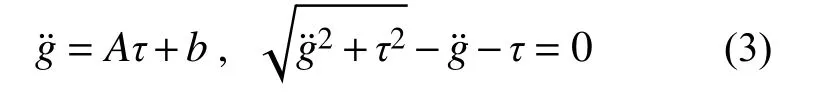
利用高效的非線性方程求解器進行計算。實際上，將單邊約束力與輪軌縫隙函數的互補關系改寫為加速度層面的互補關系，盡管在理論上可行，然而一旦積分過程中縫隙速度的數值解出現誤差，縫隙函數的違約量將不斷增長，進而使輪軌處于不真實的嵌入狀態，使得數值解偏離真實解。此時，將互補關系均勻化是一種驗證可行的策略。

三代核環吊主梁跨度大，承載能力高。為了防止豎向地震作用下部件上拋誘發脫軌行為，各部件之間安裝有防震反鉤以及緩沖器等裝置。在如此復雜的接觸狀態下，整個地震階段的長尺度運動和局部極短時間尺度的接觸碰撞相耦合[14]，這些時空多尺度耦合特性也給整體系統動力學方程的求解帶來了很大的困難。

綜上所述，準確描述輪軌之間的粘滑效應是核環吊地震瞬態動力學分析的關鍵。為此，本文在前期研究[15]的基礎上，引入LuGre模型[16 ? 17]來反映輪軌之間的stick-slip效應，進而以虛功率原理為依據，建立考慮防震反鉤、小車緩沖器的整體系統動力學方程，分析不同強震激勵下的機構位移響應和動態接觸力，討論起重量、起升高度、主動輪鎖定狀態對核環吊地震響應的影響。

1 動力學模型

輪軌間粘滑效應和瞬時跳軌行為是影響核環吊體系安全性的重要因素，本節詳細介紹了考慮粘滑效應的摩擦模型以及綜合考慮接觸/碰撞的線性互補模型，在此基礎上推導全局動力學模型。

1.1 摩擦模型

LuGre摩擦模型將摩擦力Fτ表示為法向接觸力FN的連續函數：

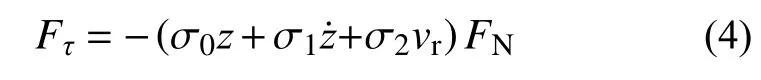
式中：z為豬鬃平均變形，作為動力學方程的附加狀態變量引入； σ0和 σ1分別為豬鬃平均變形剛度和變形阻尼系數； σ2為粘性阻尼系數。經典的LuGre模型中，鬃毛的變形量可由如下微分方程確定：

式中，非負函數g(vr)反映了靜動摩擦狀態切換時的Stribeck效應，可表示為：

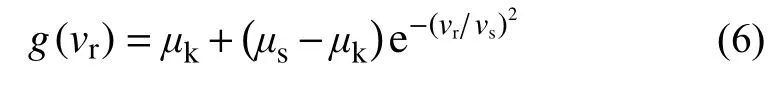
式中：μs、μk分別為靜、動摩擦系數；vs為Stribeck速度。

文獻[16]結合大量的實驗數據表明，在相對速度振蕩時的不穩定狀態下，遲滯環表達的摩擦滯后現象往往是順時針的。為此，該文給出了一種修正的LuGre模型，其控制方程可表示為：

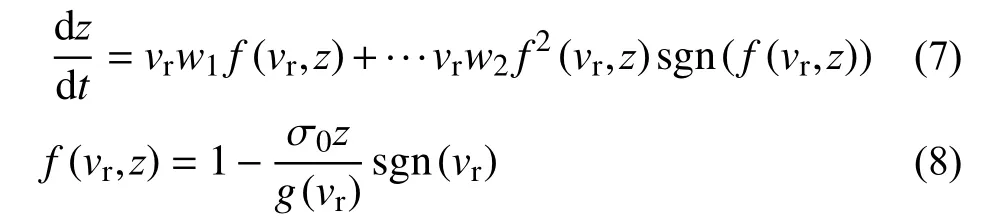
式中，w1、w2為權重系數，當w1=1、w2=0時，模型退化為標準的LuGre模型。

LuGre模型用一階微分方程刻畫了庫侖摩擦、預滑動、可變靜摩擦力、Stribeck摩擦以及摩擦滯后等摩擦現象，因而得到了廣泛的應用。但在求解實際問題時，仍需注意以下因素：

1) 參數辨識：LuGre模型對摩擦的描述能力取決于參數辨識的精度，其中靜態參數和動態參數的取值對結果影響很大，往往需要大量的實驗和辨識得到[18 ? 19]，本文選用文獻[9]辨識得到的結果作為輸入量；

2) 積分器的選擇：豬鬃剛度一般取值較大，從而給系統動力學方程引入較大的剛性(stiffness)。采用常規積分器求解時易誘發摩擦力的振蕩。建議選用剛性積分器，例如Matlab ode15s或ode23tb進行求解；

3) 積分步長：摩擦力的求解與系統狀態密切相關，以較大步長進行數值積分容易忽略摩擦過程的細節，使得摩擦力失真；

4) 求解精度控制：剛性積分器在高精度下濾波效果失效，系統方程的數值形態變得極差，數值解難以在可接受的時間內完成。

1.2 法向接觸力模型

核環吊主要接觸點如圖2所示，包含4組大車行走機構、4組大車防震反鉤、6組小車行走機構、2組小車防震反鉤、4組水平導向裝置以及主梁上方軌道四角安裝的4組緩沖器，共44個接觸點。

圖2 核環吊接觸點Fig.2 Contact points of nuclear polar crane

小車主動輪、從動輪位置如圖3所示。主動輪成功制動后依靠靜摩擦力將小車維持在既定位置。若主動輪來不及鎖定，則主動輪與軌道之間為滾動摩擦。

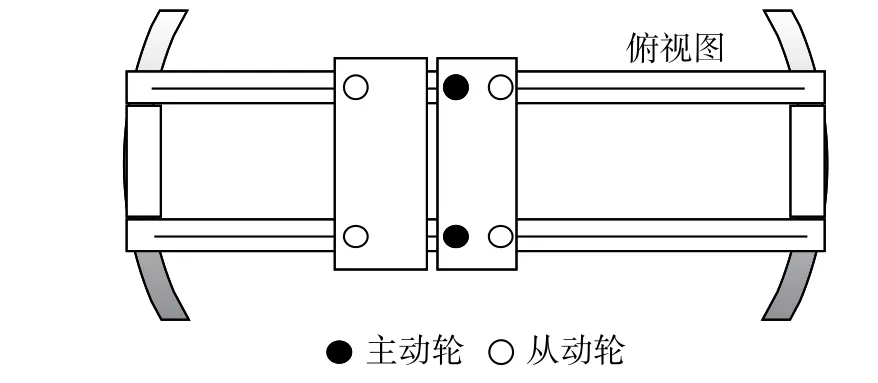
圖3 主動輪與從動輪Fig.3 Driving and driven wheels

引入互補理論描述法向接觸力FN和輪軌縫隙δ之間的互補關系：

在速度、加速度層面可等價為：

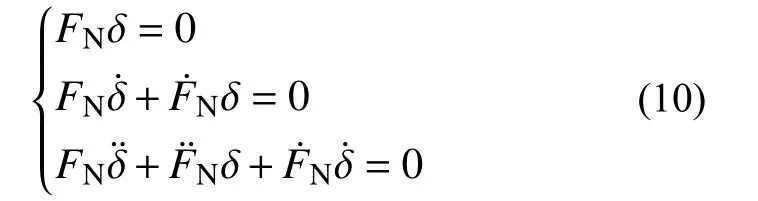
與之等價的非線性方程可寫為：

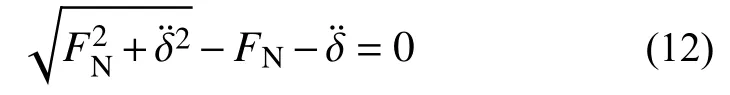
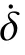
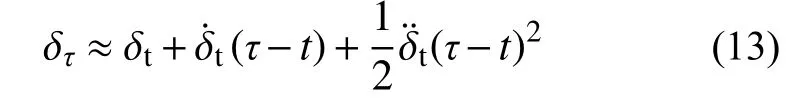
均勻化的縫隙函數可表示為：

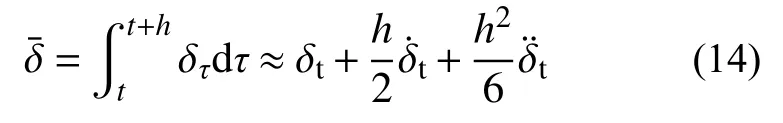
進而可將互補關系式(9)改寫為：

相應的非線性方程組可改寫為：

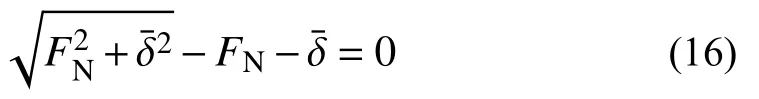
含摩擦系統的動力學方程可寫為如下形式[14]：

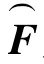
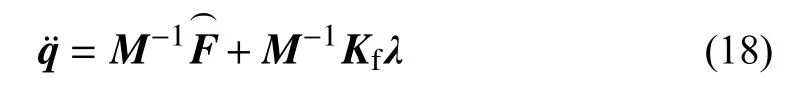
式中，Kf為接觸點虛速度變換陣組成的矩陣，各接觸點法向接觸力和切向摩擦力可綜合表示為：

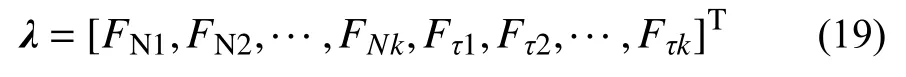
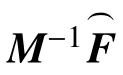
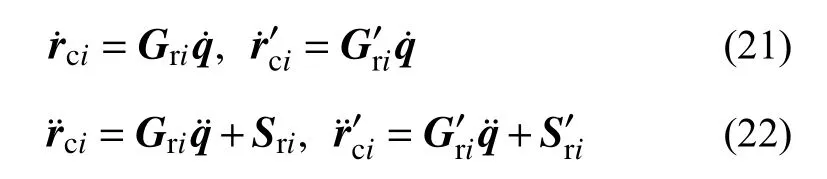
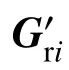
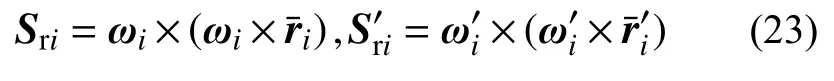
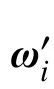
綜合式(15)～式(16)、式(21)～式(22)，第i個接觸點縫隙函數及其變化率可表示為：

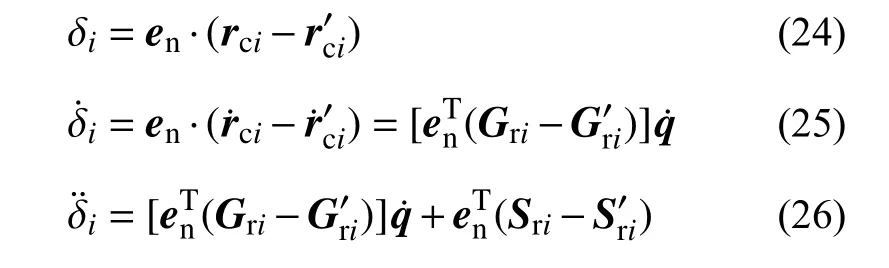
式中，en為接觸點法向單位向量。

仿照式(20)、式(24)～式(26)可簡寫為：

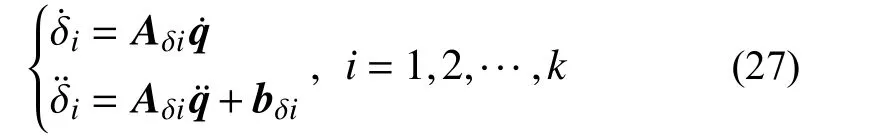
或簡寫為矩陣形式：

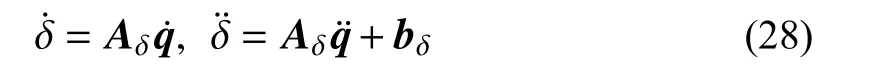
其中：

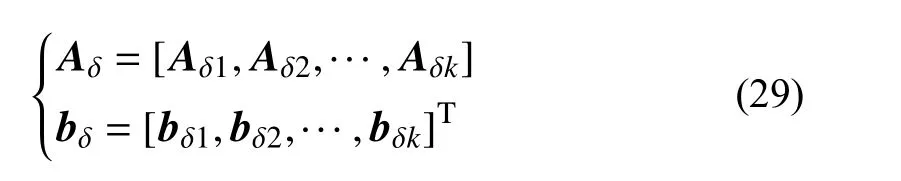
綜合式(20)、式(28)，縫隙函數二階變化率可以表示為接觸力和摩擦力的線性函數：

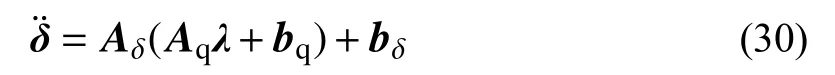
并進一步寫為：

式中：Ac=AδAq；bc=Aδbq+bq。

由式(15)、式(28)、式(31)，可得到均勻化縫隙函數：

進而得到如下線性互補方程：

1.3 整體系統動力學方程

由式(33)所述的線性互補模型，可將核環吊各部件的動力學方程通過輪軌關系聯系起來：

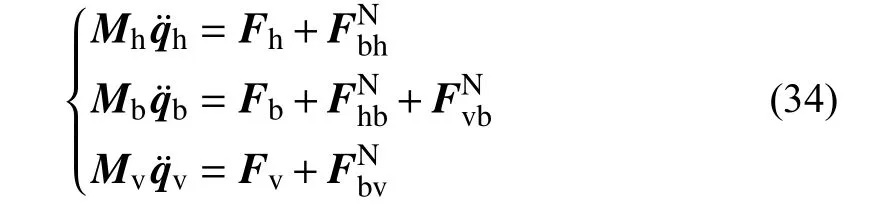
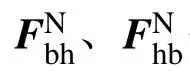
式(34)中，安全殼動力學方程包含了地面運動對系統動力學方程的貢獻，其中：

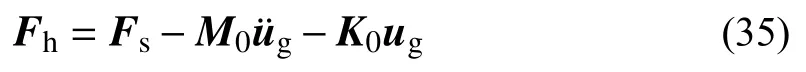
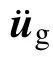
依據虛功率原理，接觸力對各部件動力學方程的貢獻源于：

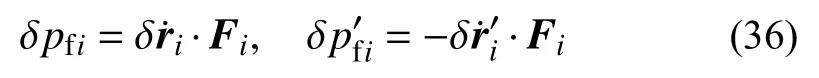
其中：

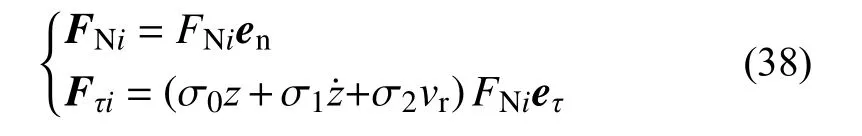
由此可將接觸力合力表示為：

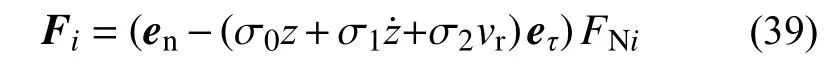
將式(39)代入式(36)并結合接觸點虛速度與廣義速度的變換關系，有：

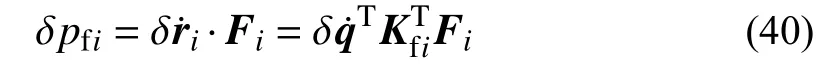
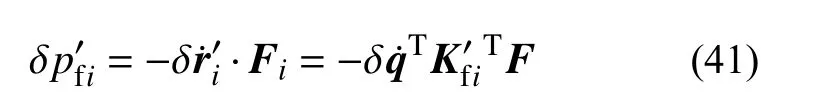
將式(34)改寫為式(20)的形式，按照式(20)～式(33)的遞推關系得到關于接觸力與均勻縫隙函數的線性互補方程，通過非線性迭代可求解瞬時接觸力。

采用上述方法建立系統動力學方程，與傳統方法相比有如下優勢：

1) 所提模型解除了部件必須綁定的限制，能夠精細分析輪軌間瞬態接觸/碰撞動力學行為；

2) LuGre摩擦模型能夠反映部件間的粘滑效應(亦即開關效應)，與實際情況更相符，避免了傳統修正模型在速度零點處的蠕動效應；

3) 能夠綜合考慮平順接觸和跳軌瞬時的碰撞效應，不必引入額外的本構關系描述接觸，也不必在每一個碰撞瞬時終止積分器來解算碰撞前后系統狀態的變化；

4) 由于模型中的高頻成分在建模階段被濾除，因此整體動力學方程中不含偽高頻振蕩，保證了數值解的穩定性，可采用常規積分器求解，與傳統商業有限元軟件相比計算效率高。

綜合上述過程，考慮粘滑效應的核環吊抗震分析可采用圖4所示的計算流程圖表示。

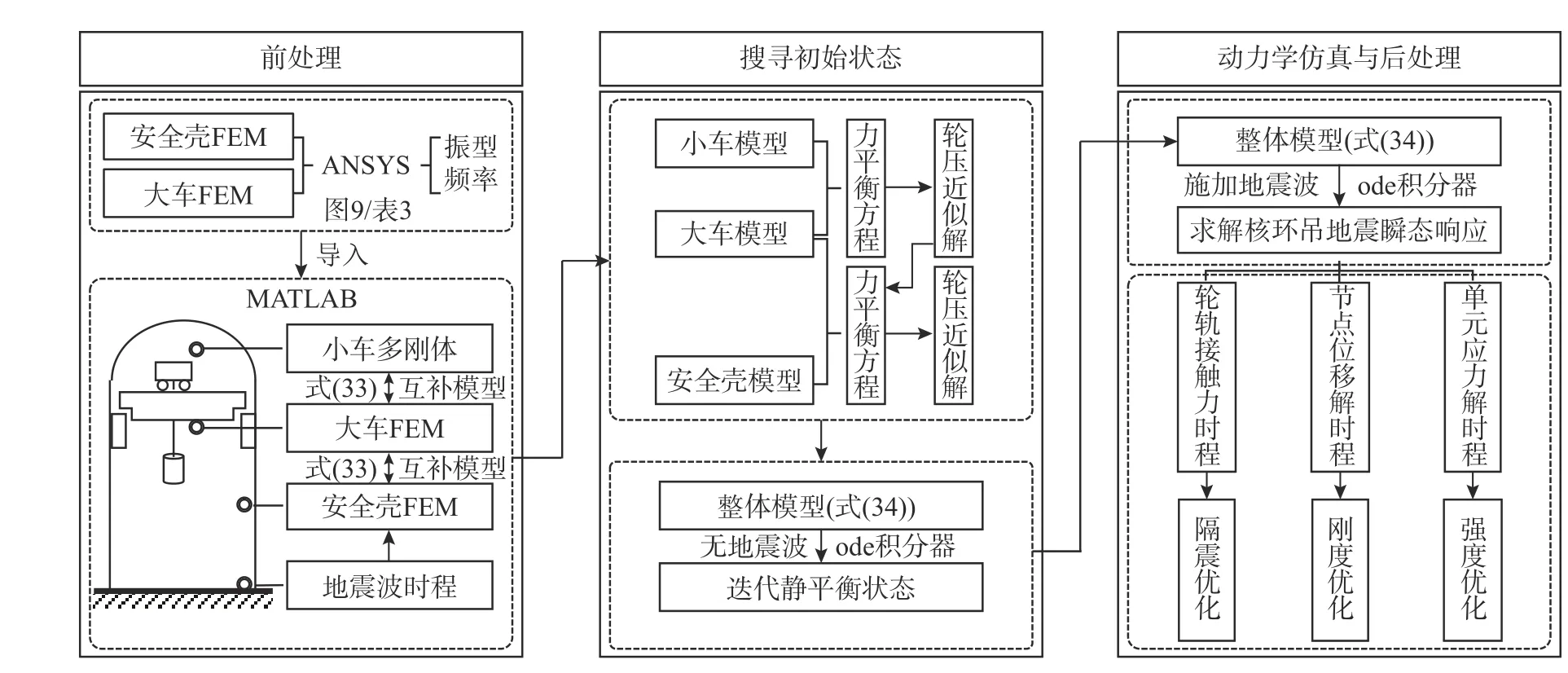
圖4 核環吊抗震分析求解流程圖Fig.4 Flow chart of seismic analysis for nuclear polar crane

1.4 輸入地震動與工況組合

若地震預警及時，則各行走機構在地震來臨前成功制動，依靠靜摩擦力避免在水平強震下發生滑移；若預警滯后，則部件可能在強震下發生大范圍的相對滑動[20]。考慮到這些情況，表1列出了本文部分典型工況的載荷組合特征。同時，為了考慮強震對核島安全殼結構-機構相互作用的影響，同時檢驗所提模型對部件跳軌行為的反映能力，參照文獻[5] 分別按照運行安全地震動(OBE)、極限安全地震動 (SSE)和超設計基準地震動 (ULE)作為輸入，從PEER地震數據庫[21]選擇了8組強震記錄作為基礎激勵，如表2所示。其標準化的5%阻尼比反應譜如圖5所示。在設備主頻范圍2 Hz～10 Hz內，與我國《核電廠抗震設計標準》(GB 50267?2019)[3]中的基巖和硬土標準反應譜以及美國RG1.60譜符合良好。此外，還依據《核電廠抗震設計標準》[3]規定的反應譜擬合了兩組人工地震波進行補充計算，相應的10組水平加速度時程曲線如圖6所示(前8組為表2所示強震記錄，后2組為擬合圖5反應譜的人工地震波)。

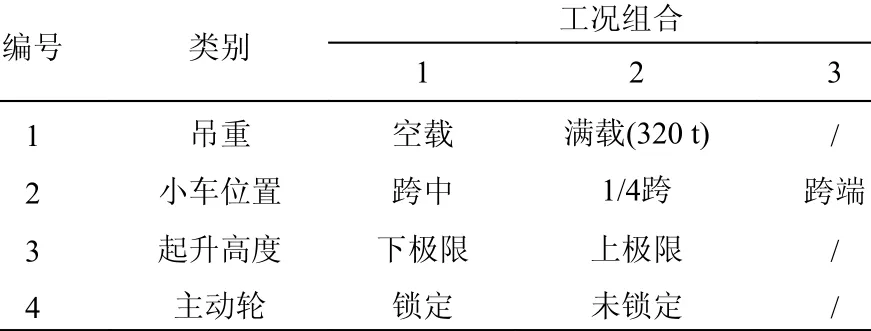
表1 載荷組合Table 1 Loading combinations

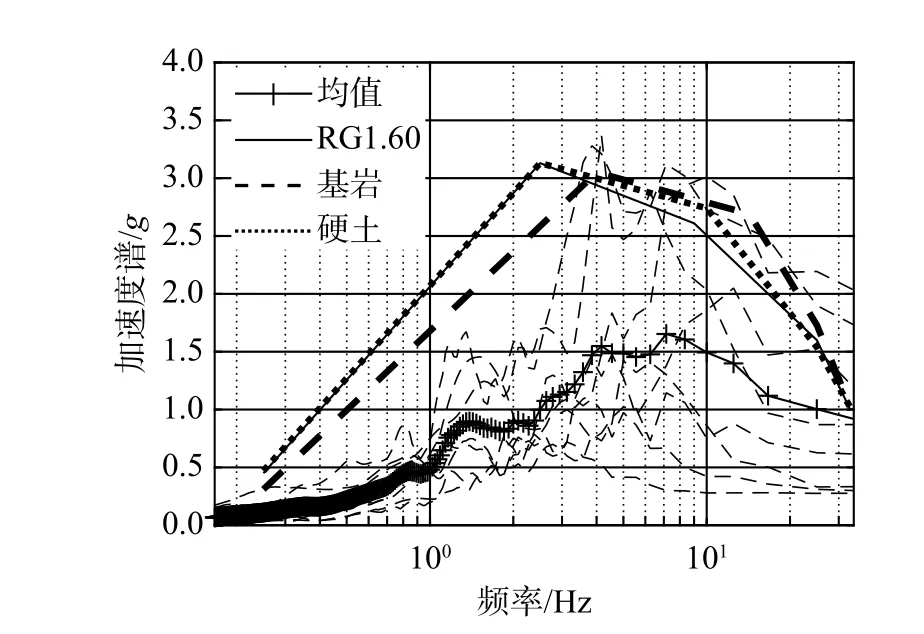
圖5 輸入地震動標準化5%阻尼比加速度反應譜Fig.5 Normalized acceleration response spectrum of selected ground motions considering 5% damping ratio

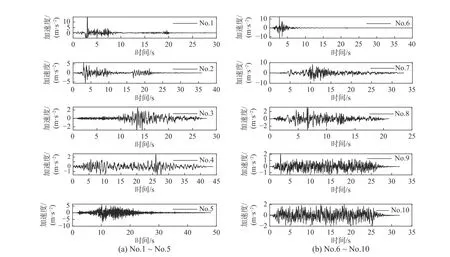
圖6 地震動加速度時程Fig.6 Time history of ground motion acceleration

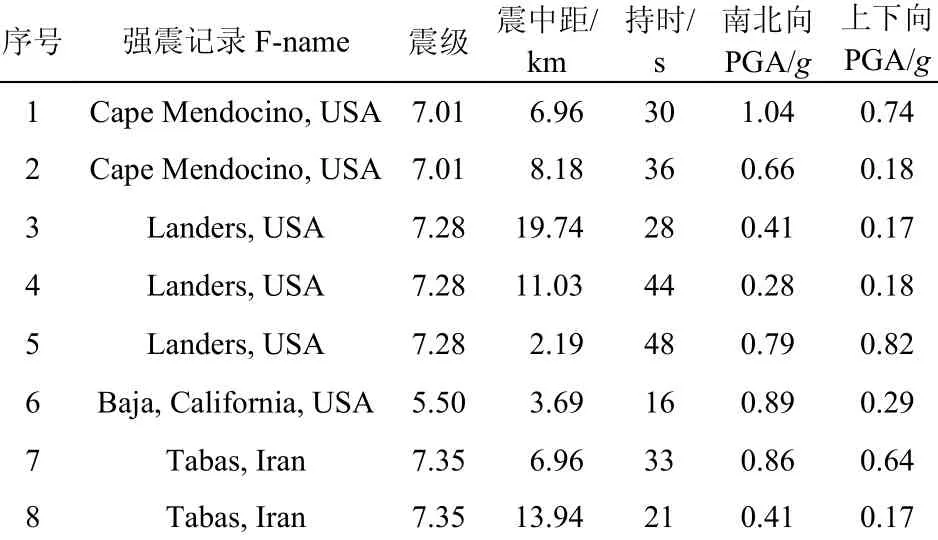
表2 輸入地震動Table 2 Input ground motions

2 摩擦模型比較

強震激勵下小車的運動狀態與所采用的摩擦模型有密切的關系。為此，首先采用LuGre模型以及修正的庫侖摩擦模型分析輪軌間摩擦力，并與標準的庫侖摩擦模型進行比較。

LuGre模型參數取值如下： σ0=106N/m，σ1=350N·s/m ， σ2=0 ，vs=8×10?4m/s，主動輪鎖定時的靜、動摩擦系數μs=0.3 、μk=0.2。滾動摩擦系數μr=0.007。所采用的修正的庫侖摩擦模型可表示為：

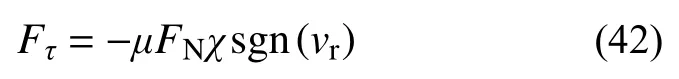
式中，χ為關于相對速度vr的分段函數：

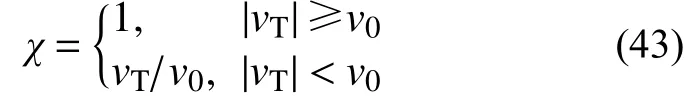
圖7和圖8分別給出了采用記錄2 Cape波和記錄6 Baja波得到的小車與其軌道之間的相對滑移量時間歷程曲線。從圖中可見，主動車輪鎖定后，在強震段均發生一定的滑移，其中在Cape波的作用下小車相對滑移量為10 cm，而在Baja波的作用下滑移了5 cm。LuGre模型計算結果與標準庫倫摩擦模型吻合。但修正的庫倫摩擦模型計算結果失真：Cape波下，標準庫侖摩擦模型計算得出5 s后無相對滑移，但修正的庫倫模型仍計算出較大的滑移量；Baja波下，盡管在最后階段車輪回到初始位置附近，但整個強震過程中的動態滑移量與其余兩個模型有著顯著的差異，因此該模型無法反映靜-動摩擦狀態切換時的stick-slip效應。

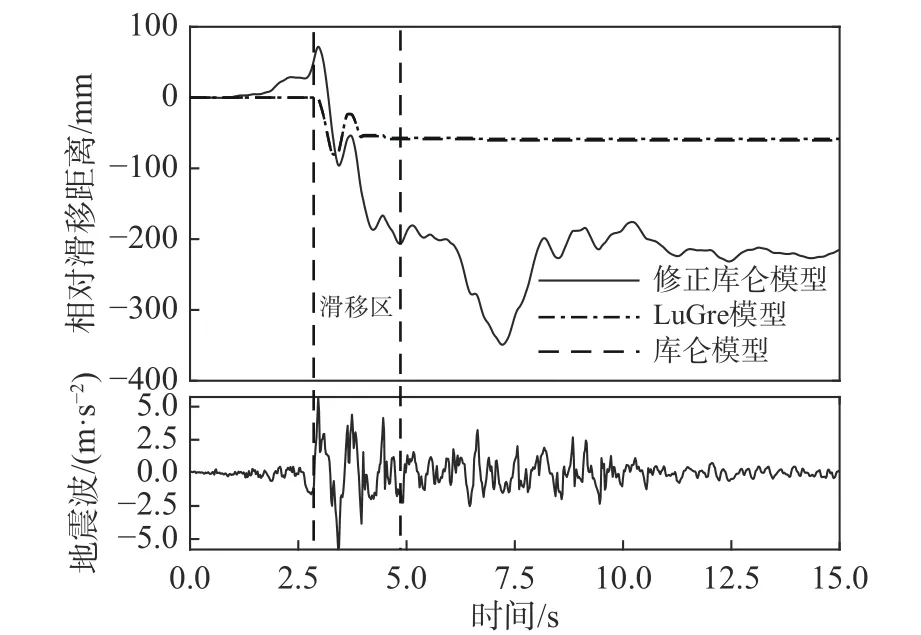
圖7 Cape波相對滑移時程Fig.7 Relative displacement time history curve of Cape wave

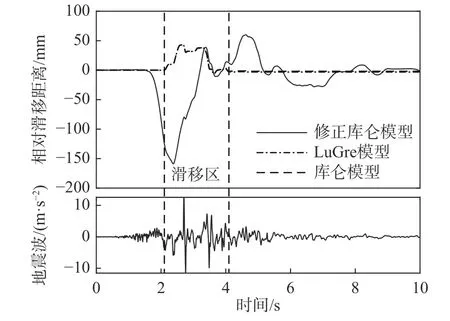
圖8 Baja波相對滑移時程Fig.8 Relative displacement time history curve of Baja wave

3 核島-核環吊耦合系統地震響應

對核島-安全殼耦合體系進行瞬態接觸動力學分析采用的參數和單元信息如下：安全殼內徑43 m，壁厚42 mm，由三段筒體和上、下封頭依次吊裝而成，并安裝有加勁肋，采用shell181單元模擬。大車主梁采用beam188單元模擬(主梁內部附屬電氣設施簡化為分布質量)，前、后主梁跨度10 m、縱向長度為38 m；行走機構和導行機構的剛度忽略不計，將其視為剛體依附在柔體模型上；忽略小車架體的變形，將小車抽象為剛體。經驗算，起升鋼絲繩在強震階段基本沒有發生松弛，因此將起升鋼絲繩和吊重簡化為剛性雙擺。邊界條件設定如下：安全殼底端固支，大車、小車可自由運動，輪軌無綁定，按照1.2小節所提方法計算瞬時接觸力。

3.1 結構模態分析

為了提高安全殼-核環吊耦合體系動力學方程的數值性態和求解效率，本文首先對安全殼/主梁結構進行模態分析，進一步將分析結果導入到matlab中作為后續建模的基礎。由于本文解除了輪軌之間的綁定，因此環吊大車結構模態將包含6組剛體模態，反映了6種微幅剛體運動模式。圖9給出了主梁前9階模態和安全殼前3階模態的結果，表3列出了結構的前若干階固有頻率。

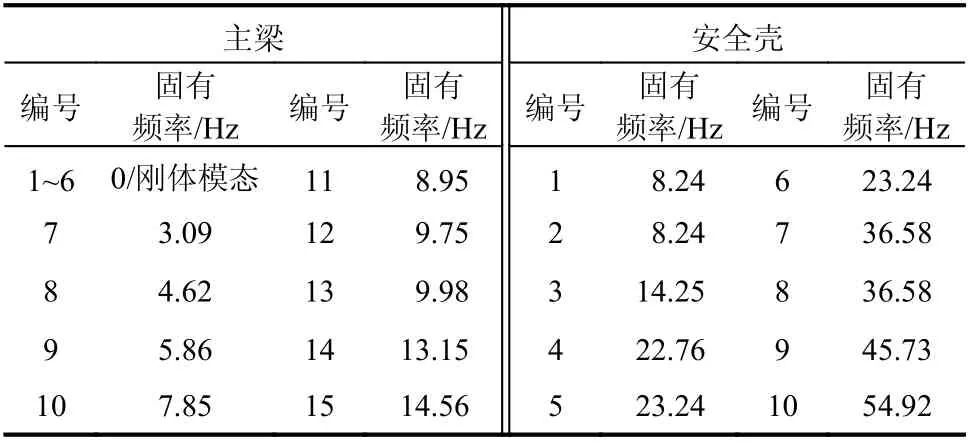
表3 結構固有頻率Table 3 Natural frequency of structure

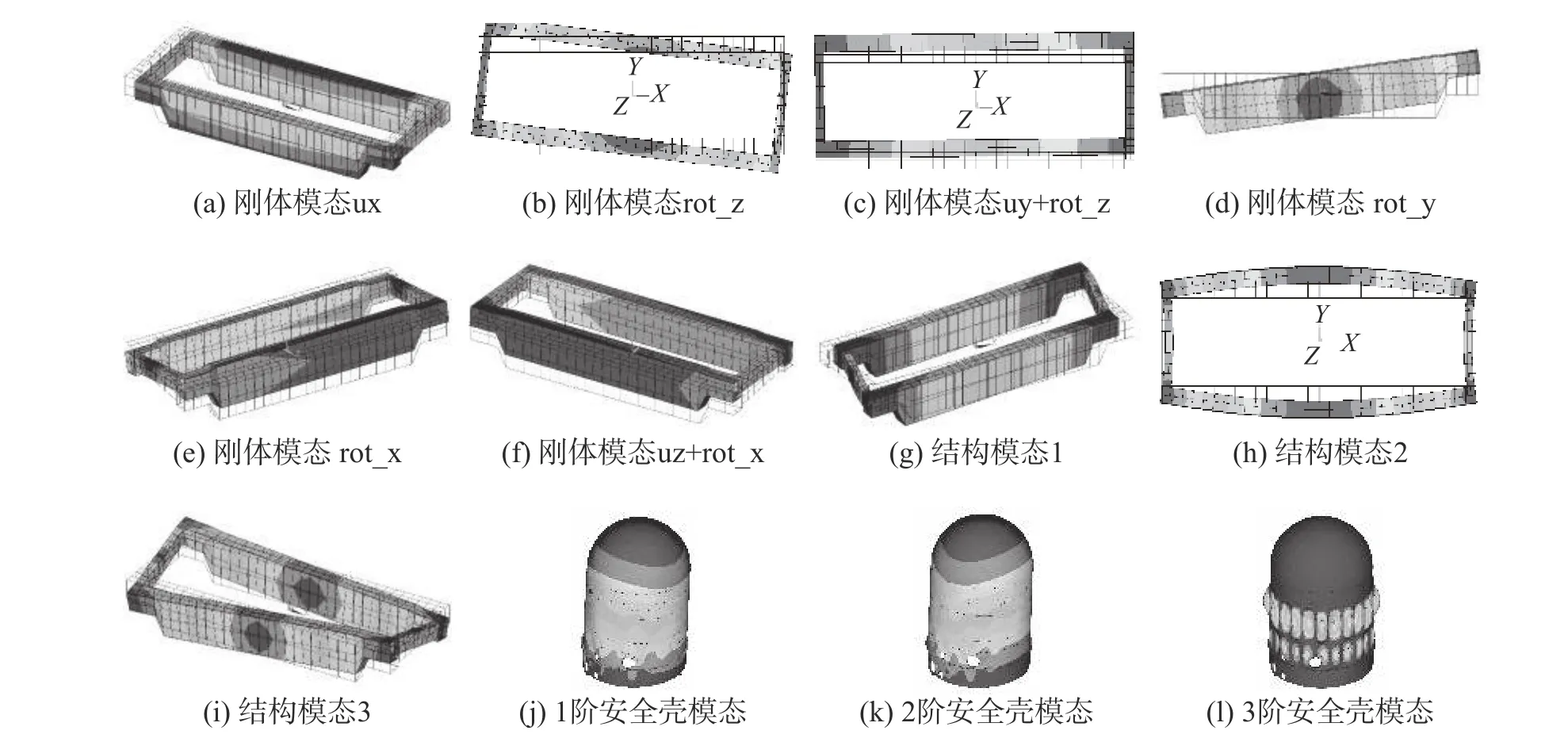
圖9 主梁、安全殼模態Fig.9 Modal results of girder and containment vessel

3.2 大車跳軌分析

表4統計了10組地震作用下各工況組合下大車跳軌情況。其中，1號、2號、6號、7號強震下大車車輪組接觸力瞬時歸零，發生跳軌現象。1號、2號地震下所有工況均發生跳軌。地震6下部分工況發生跳軌(空載工況均發生跳軌，滿載工況未發生跳軌)。結合表2可見，大車跳軌情況不僅與豎向加速度峰值有關，也與其水平分量有關。地震2的豎向加速度峰值僅為0.18g，遠小于地震5的0.82g，但其南北向峰值加速度達到了0.66g，且幅值變化較快，因此產生了瞬時跳軌。地震5的水平/豎向加速度峰值均大于地震2，但其加速度曲線變化程度不如地震2劇烈，故并未發生跳軌。第3號、4號地震記錄的豎向加速度峰值與2號地震波相當，但其水平加速度較小，因此未發生跳軌。7號地震波兩個方向的峰值加速度較大，發生跳軌現象。

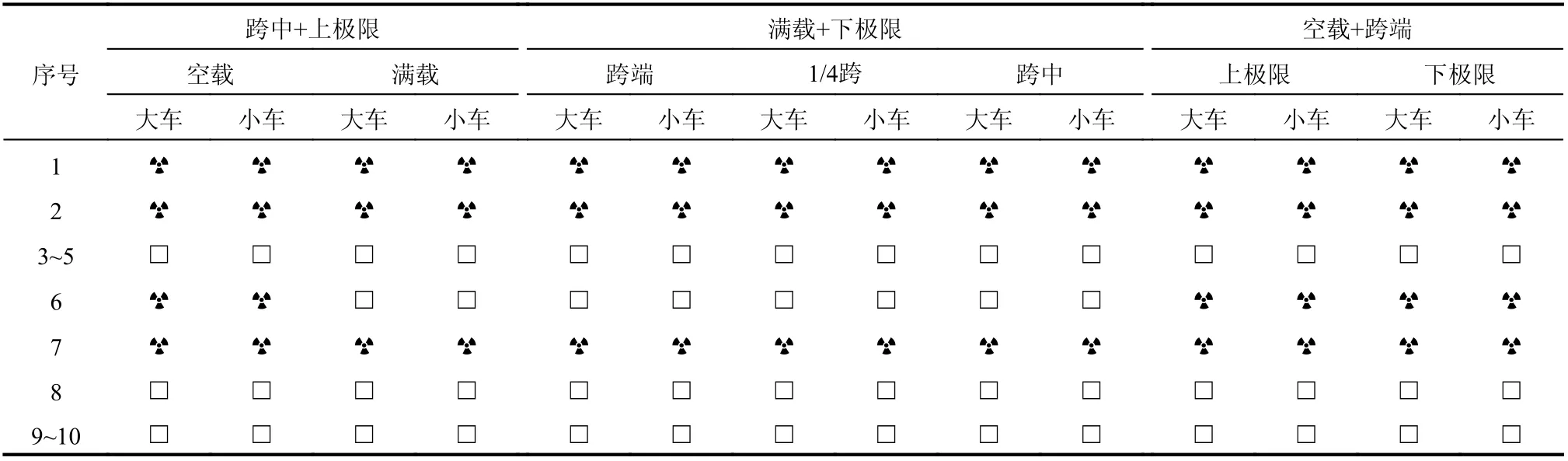
表4 跳軌情況統計Table 4 statistics of derailment phenomenon

圖10給出了滿載320 t、吊重位于上極限、小車分別位于跨中、1/4跨和跨端三種條件下的峰值輪壓和其靜輪壓的對比。由于1號、2號、6號、7號地震下大車發生跳軌，相應的峰值加速度遠大于靜輪壓，并且與小車所處的位置有關。由圖10(a)可見，小車位于跨中時跳軌情況最為嚴重，瞬時輪壓遠大于靜輪壓，1號、3號、4號接觸點碰撞力極大，2號車輪跳起量較小，跳軌時的瞬時輪壓與靜輪壓幅值相當。當小車位于1/4跨或者跨端時雖然也發生跳軌現象，但其峰值輪壓遠小于小車位于跨中時的跳軌輪壓，表明強震來臨時若小車位于跨中是最不利位置，因此在地震作用下小車停靠在兩側位置對于結構抗震最為有利。除1號、2號、6號、7號地震外，其余地震作用下大車均未發生跳軌現象，因此峰值輪壓與靜輪壓相比雖然有所增加，但幅度不大。

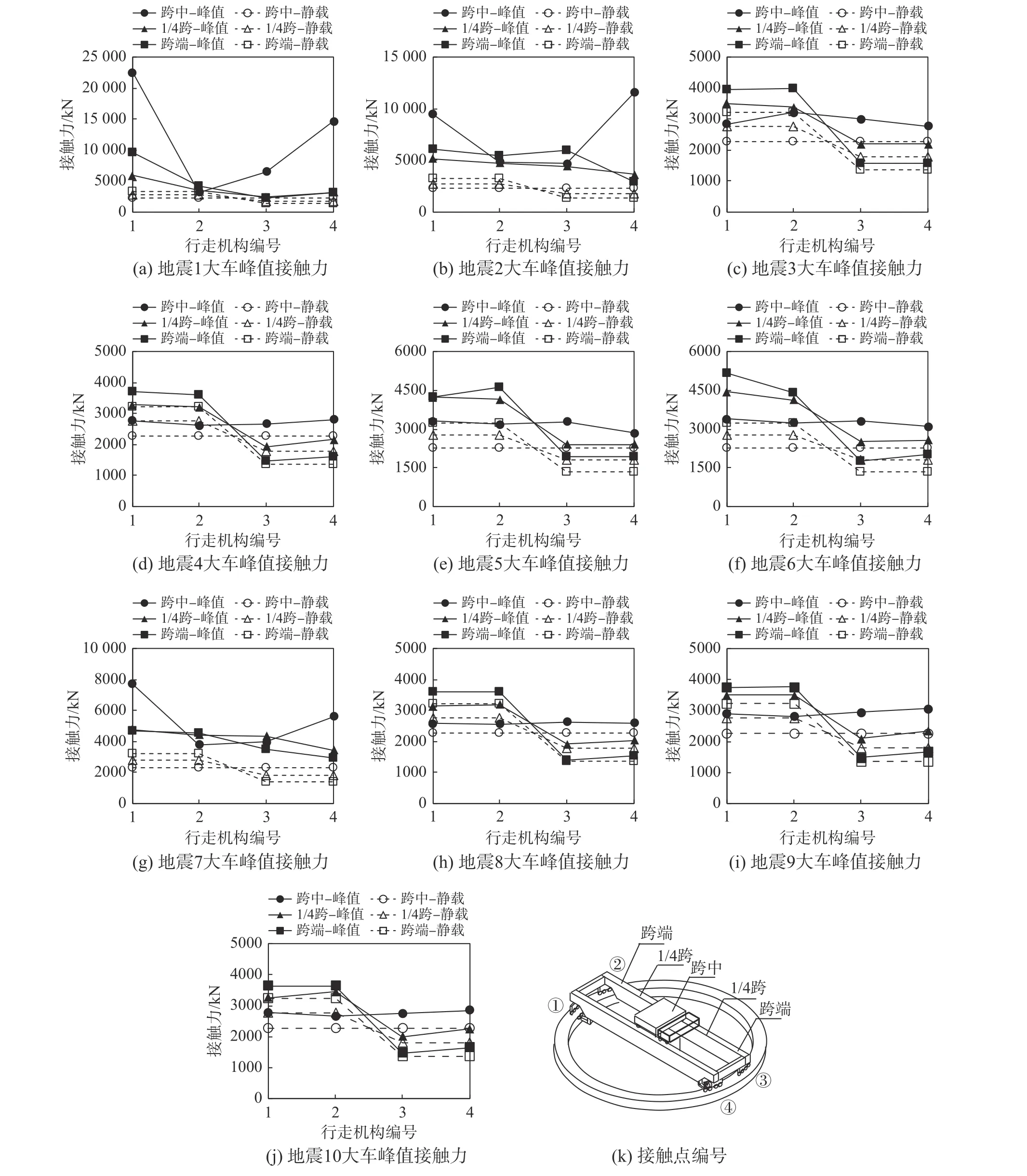
圖10 峰值輪壓與靜輪壓比較Fig.10 Comparison between peak wheel pressure and static wheel pressure

在跳軌工況中，1、2號地震作用下輪壓變化最大，最大輪壓與靜輪壓的比值分別為9.9和5.1，7號地震作用下該比值為3.4。其余地震作用下峰值輪壓與靜輪壓的比值均未超過1.5。當小車位于1/4跨時，1號地震的峰值輪壓/靜輪壓之比降低到2.1，在跨端時為2.9。

圖11給出了主梁加速度時程曲線和相應的傅里葉譜。其中，圖11(a)、圖11(c)、圖11(d)、圖11(e)給出了4組跳軌工況下(跨中/下極限/滿載)主梁節點加速度時程和地面運動對比，圖11(b)、圖11(d)、圖11(f)、圖11(h)給出了相應的傅里葉幅值譜。從中可見，進入強震階段后主梁運動被放大誘發跳軌，碰撞后激發了主梁的高頻振蕩(見圖11(b)傅里葉譜)，從而激發了后續的次碰撞。

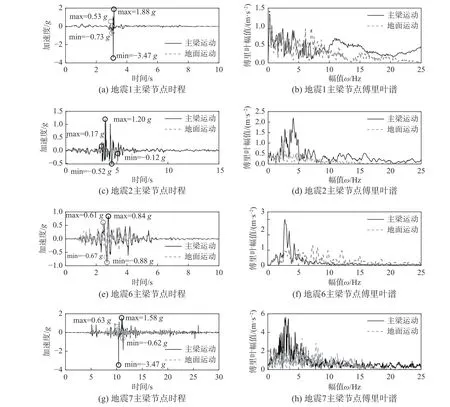
圖11 主梁加速度時程與傅里葉譜Fig.11 Acceleration time history and Fourier spectrum of main girder

3.3 小車滑移量分析

圖12給出了小車位于跨中、吊重滿載/空載以及主動車輪組鎖定/未鎖定四種組合工況下的小車相對滑移量曲線。結果表明：主動車輪組及時鎖定后，小車能夠將自身維持在既定位置不至于滑動太遠。若制動失效，則整個強震階段小車均處于相對運動狀態。此外，由于空載時小車提供的正壓力較小，因此維持其自身位置的最大靜摩擦力也較小，相比滿載情況空載時產生的相對位移稍大。以圖12(d)為例，其水平峰值加速度僅為0.28g，“滿載+鎖定”工況下滑移量為零，“空載+鎖定”工況下產生滑移。圖12(e)中，水平地震波在10 s左右到達峰值0.79g，豎向地震波峰值達0.82g。盡管主動車輪組已經鎖定，滿載或空載情況下滑移量均超過了1 m。圖12(g)中，水平加速度在15 s之后衰減到0.23g，但豎向加速度再次增大到0.49g，摩擦力進一步降低，從而使小車產生了較大的滑移。

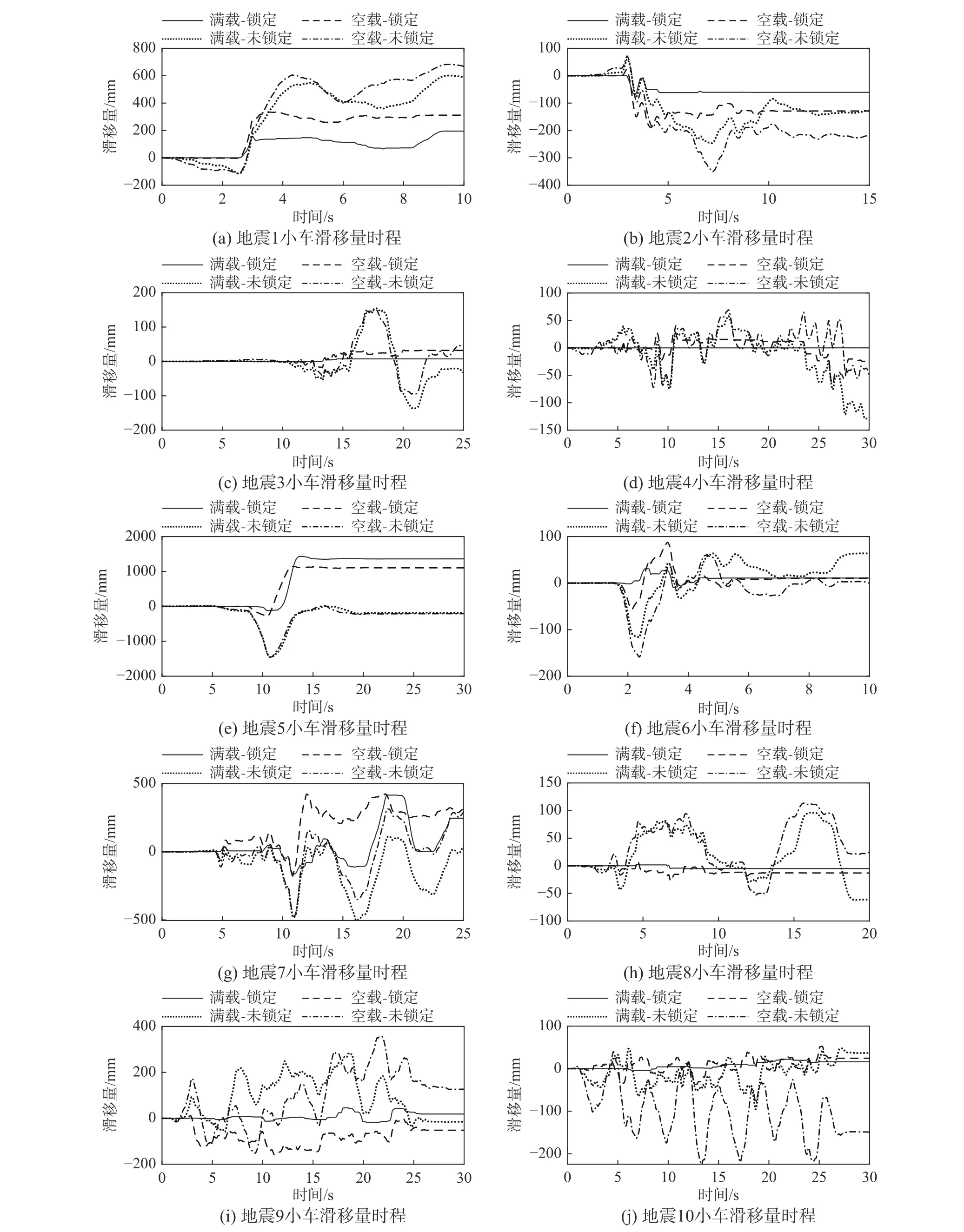
圖12 小車-主梁相對滑移量Fig.12 Relative slip between trolley and main girder

綜合以上分析，鎖定驅動輪可防止部件在強震下發生滑移，避免整機或吊重與環境發生碰撞。同時驗證了摩擦模型的有效性。

3.4 應力分析

選取前主梁為研究對象，滿載工況下各單元最大應力如圖13所示。圖13中可見，主梁在最大應力發生在兩側。原因在于水平地震作用下水平隔振裝置與軌道發生沖擊，由于隔振裝置依附于3號、8號單元下翼緣，導致了這兩個單元應力遠大于其它單元。以地震1為例，3號單元最大應力是跨中6號單元最大應力的3倍，其余地震作用下的主梁最大應力分布呈現相似的特點。圖13(g)中，主梁3號單元一側水平隔振裝置與軌道發生較大的沖擊，因此單元最大應力高于另一側相應位置的單元。除1號、2號、6號、7號地震外，其余地震水平峰值加速度較小，水平隔振裝置所受沖擊較低，并未出現圖13(a)中明顯的尖點，但均呈現出“雙峰”的特點。

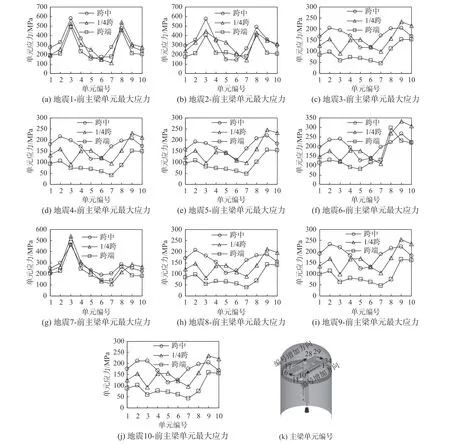
圖13 前主梁單元最大應力Fig.13 Maximum stress of the front bridge element

3.5 主鉤拉力分析

圖14統計了滿載條件下，小車分別位于跨中、1/4跨以及跨端時主鉤的最大、最小拉力。1號地震下小車跳軌，其主吊鉤組最大拉力可達靜拉力的2.5倍。結合圖10可見，小車位置對大車輪壓有影響，但對主鉤拉力影響較小。在地震2和地震7的作用下，小車處于跨中時主鉤最小拉力為負值，表明主鉤繩索發生松弛，不宜再將提升系統簡化為剛性桿。除了4號、8號地震外，其余地震下主鉤拉力放大倍數均大于1.6，或可在提升系統中考慮安裝緩沖裝置，從而降低主提升系統鋼絲繩受到的瞬時沖擊，防止鋼絲繩發生破斷后造成危險載荷跌落。

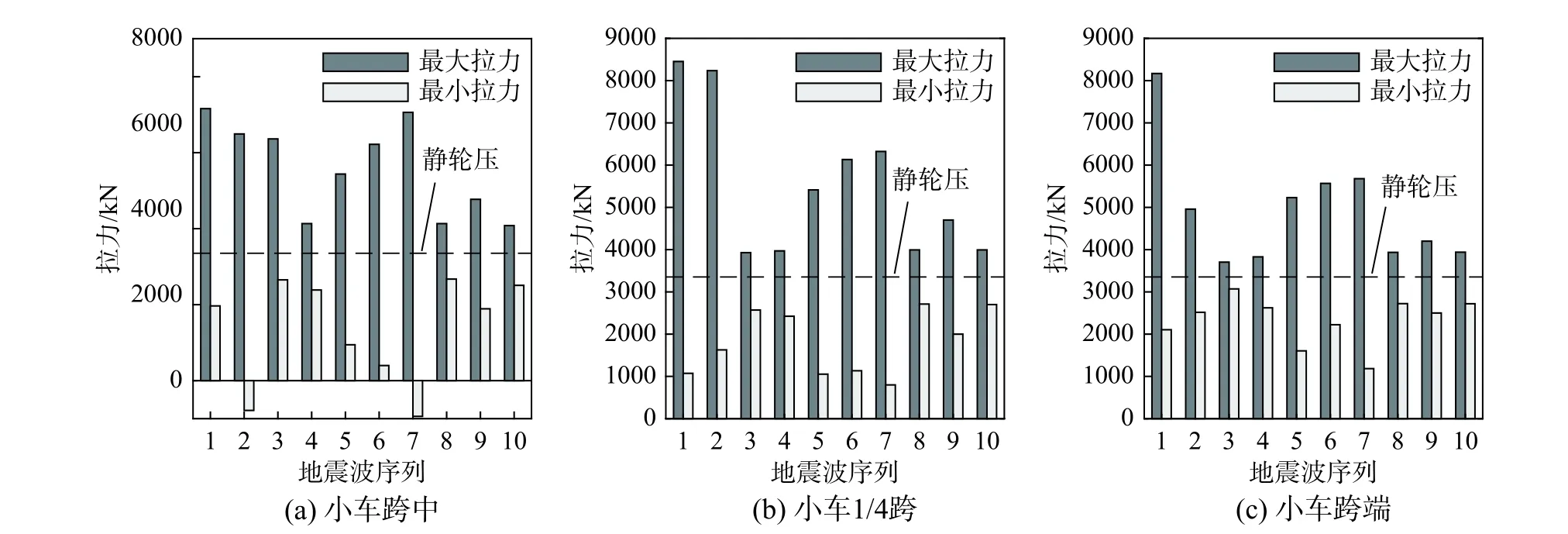
圖14 主鉤拉力對比Fig.14 Tension comparison of main hook

4 結論

本文建立了考慮粘滑效應的核環吊瞬態動力學分析模型，分析了強震作用下部件的跳軌行為以及stick-slip現象，得出如下結論：

(1) 強震下核環吊行走機構的制動性能是將整機維持在既定位置的關鍵因素，宜采用反映粘滑效應的動態摩擦模型進行分析；

(2) 對于含LuGre模型的動力學模型，從參數辨識、積分器的選擇、積分步長的確定以及求解精度方面進行了深入討論，給出了LuGre模型的適用條件；

(3) 核環吊發生跳軌是水平地震和豎向地震共同作用的結果。小車位于跨中時峰值輪壓最大，位于1/4跨或跨端時峰值輪壓降低。小車宜停靠在主梁兩側以應對強震；

(4) 對比了各工況下主鉤拉力。強震作用下主鉤拉力最高可達靜拉力的2.5倍，且與小車位置無關。宜考慮在提升系統中增加隔震緩沖裝置；

(5) 核環吊發生跳軌時的間隙量較小，但跳軌瞬時的沖擊力極大，后續可考慮在行走機構和主梁之間安裝緩沖裝置，避免行走機構發生破壞；

(6) 個別工況下提升系統最小拉力為負值，表明鋼絲繩發生松弛，再次張緊時將誘發沖擊。后續研究將細化鋼絲繩建模。