帶冷卻氣流的亥姆霍茲共振器的聲類比模型1)

甘振鵬 楊 東

(南方科技大學工學院力學與航空航天工程系,廣東深圳 518055)

引言

為響應國家碳達峰、碳中和目標下對煙氣污染治理的需求,低污染排放的燃氣輪機和航空發動機的發展日益需要滿足更嚴格的環保要求[1].相比于傳統燃燒方式,貧燃預混燃燒因能顯著降低NOx排放而被廣泛應用[2-3].但貧燃預混燃燒會使燃燒室更容易受到熱聲振蕩的影響—不穩定燃燒產生聲音,該聲音傳到燃燒室邊界被反射回來進一步擾動燃燒進而產生更多聲音;該正反饋過程可能產生巨大的壓力振蕩[4].燃燒熱聲振蕩所造成的危害小到干擾燃燒過程,產生機械振蕩和噪音,使污染控制失效,大到減少部件工作壽命,損壞燃燒室部件,甚至導致發動機停機以及嚴重空難事故[5].實現貧燃預混燃燒的關鍵技術之一是避免和抑制燃燒熱聲振蕩.

抑制燃燒熱聲振蕩的方法主要有主動控制和被動控制.亥姆霍茲共振器(HR)由于其簡單的結構、較高的經濟性和良好的吸聲性能而被作為一種典型的抑制熱聲振蕩的被動控制裝置[6].HR 的結構一般由空腔加上頸部開孔所組成,其共振頻率可以用眾所周知的公式f=c/(2π)進行預測,其中c為HR 空腔中的聲速,而A,l,V分別是HR 頸部截面積,HR 頸部長度和HR 空腔體積.在共振頻率附近,HR 入口附近一個微小的壓力擾動會引起其頸部顯著的質量流量擾動[7],從而由于黏性效應而耗散掉聲波能量[8].將HR 應用于上述燃燒室中消除熱聲振蕩時,在HR 的背部空腔中往往會輸入取自于壓氣機后幾級的冷卻氣流,其溫度(約500 K 左右)一般顯著低于燃燒室溫度(約1000～2100 K)[9].這些冷卻氣流不僅可以保護HR 免于燃燒室內高溫燃氣的侵蝕,還能為HR 提供平均流動以提高其吸聲性能.根據HR 中有無平均流動,可分為線性模型(有平均頸流的情況,也稱為偏流)和非線性模型(無偏流)[10-15].而在以往的工作中,往往忽視了熱聲振蕩系統中HR 與燃燒室之間的溫差.比如,Dupere和Donwling[13]基于燃燒室內一維擾動量在共振器上下游之間的質量守恒和滯止焓連續關系,得到的共振器模型無法考慮前述溫差帶來的影響.但實際上,HR和燃燒室的溫差對燃燒室內聲波(及熵波)傳播的影響不可忽視.最近,Yang 等[16-17]考慮了HR 與燃燒室的溫差對燃燒室聲波的影響,并針對HR 與燃燒室之間有溫差的情況,將能量守恒方程與一維燃燒室中的質量、動量守恒方程相結合,推導出一個一維聲場中跨過HR 時的階躍條件模型,該模型將燃燒室的上、下游熵波與聲波傳遞關系轉化為一系列聲傳遞矩陣,來研究該溫差對HR 性能的影響.該研究表明共振器與燃燒室之間的溫差會在燃燒室內共振器下游產生顯著的熵波,與此同時,共振器影響燃燒室內聲波傳播的性能也被顯著地改變了.

但上述階躍條件模型無法從機理上解釋為何共振器下游會產生熵波,更無法解釋該熵波的產生如何改變共振器對燃燒室內聲波傳播的影響.針對這些問題,本工作將采用聲類比方法[18-19],通過質量、動量和能量守恒,推導出安裝有亥姆霍茲共振器的一維燃燒室管道內的聲類比形式的波動方程.該方程的源項即表示了共振器對管道內聲場影響的物理機理.然后通過引入HR 的線性模型和相關熱力學方程,以及系統邊界條件,便可使相關方程組閉合.對該波動方程作傅里葉變換至頻域中,將解偏微分問題轉化為解常微分問題,可以直觀解得方程的解,即燃燒室中HR 上、下游擾動量之間的關系.該方程具有聲類比的形式,在其右側可以直觀地看到聲源和聲耗散項,進而得到HR 所帶來的熵擾動和質量擾動對管道內聲場的影響.最后,通過與文獻[16]的階躍條件模型結果做對比來驗證該模型.

1 理論模型

1.1 安裝有亥姆霍茲共振器的一維管道聲波模型

考慮一個安裝于主系統(此處為一個一維燃燒室管道)上的HR,低于燃燒室內部溫度的冷卻氣流從HR 空腔后部穿過HR 進入燃燒室,如圖1 所示.

圖1 中,M為馬赫數,p為壓力,T為溫度,S為熵,Ac和An分別為燃燒室截面面積和HR 頸部截面面積,L為HR 頸部的長度,頂標“-”和“～”分別表示平均量和擾動量.在燃燒室中,位于共振器上游的流量參數下標為1,共振器下游下標為2,HR 共振器頸部下標為n,分別對應如圖2 所示的控制體的截面1-1,截面2-2和源項處的流量參數.

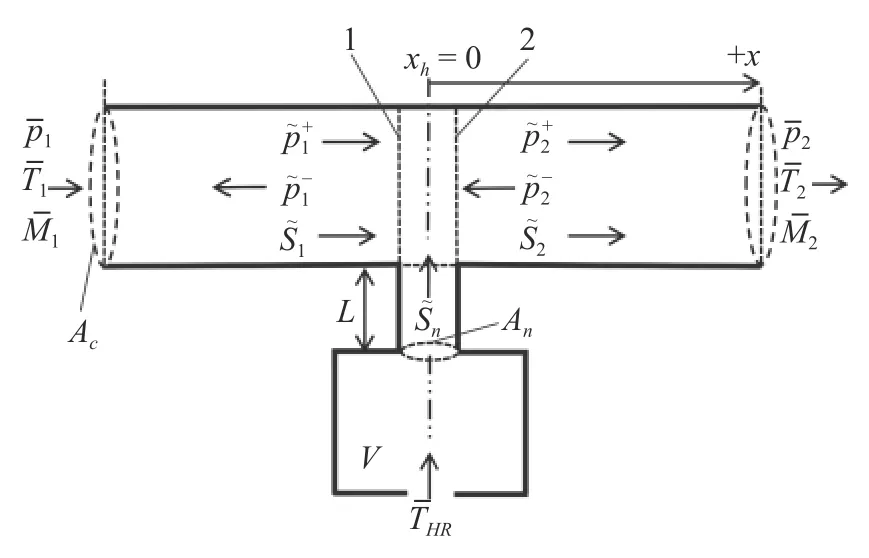
圖1 安裝有亥姆霍茲共振器的一維燃燒室管道Fig.1 A Helmholtz resonator installed in an combustor duct

圖2 無限薄的積分控制體Fig.2 Infinitely thin integral control body

由于本文只研究帶冷卻氣流的亥姆霍茲共振器對帶有高溫流體的燃燒室內聲波的影響,不考慮燃燒室內的燃燒過程本身,故在分析過程中先做如下假設:假設系統中的介質為可視作理想氣體的空氣,符合理想氣體方程p=ρRT,其中R為氣體常數 ;無黏性耗散作用;忽略體積力、所有的熱源和熱擴散.

對該一維燃燒室管道應用質量、動量和能量守恒得到

式中,u為速度,為從HR 輸入的質量流量源項,E˙為從HR 輸入的能量流量源項,δ(x)為狄拉克 δ 函數用來規定質量源項和能量流量源項的輸入位置為x=0.在燃燒室內沿著x方向上的動量是恒定的,因為在燃燒室中假定共振器頸流是徑向向內的.

在圖1 中取截面1-1和截面2-2 之間為控制體,并假設截面1-1 到截面2-2 的距離 dx無限小,如圖2所示.將式(1)對x從1-1 截面到2-2 截面積分得到

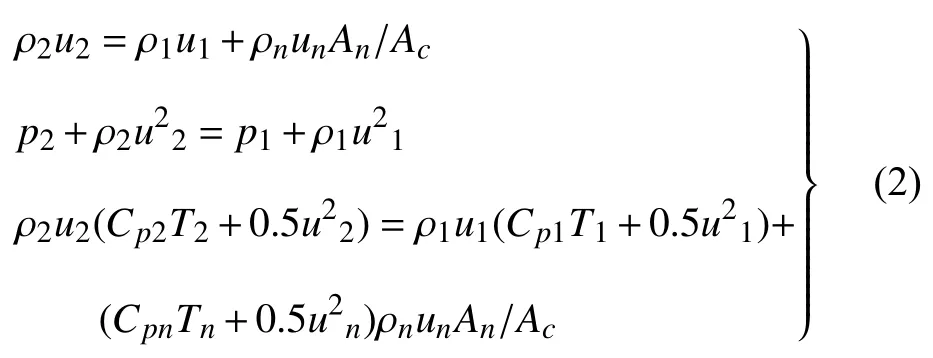
式中,Cp為定壓比熱容.式(2)等價于

式中,m,f和e分別表示質量,動量和能量流量

為了得到共振器上下游平均量的關系,對式(2)取平均量得

HR 的平均質量通量通常比燃燒室內的平均質量通量要小得多,因此燃燒室的平均流量在經過HR 后變化很小.在計算方程(5)時,考慮所以共振器上下游平均量幾乎相等,這一點從上面的計算中也可以得到.但在后續計算中,如無特別說明,使用的平均量為方程(4)的解,故使用下角標1,2 以作區分.

對方程(1)中質量和動量守恒方程做線性化,即將所有流動量表示為一個平均量和一個擾動量的和,代入原方程,忽略二階及高階擾動項,可以推導出線性化的質量和動量方程為

為了得到方程(6),假設了所有平均流量參數是沿空間是均勻(或變化緩慢),即

由于系統中存在冷熱流量動態摻混,為非等熵過程,根據能量方程可知,系統自然會產生熵波.因此,溫度擾動將包含熵擾動的影響,其推導可由能量方程給出.通過熱力學關系可以得出密度擾動與壓力擾動和熵波擾動的關系式為

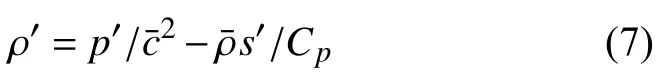
式中,s′為熵擾動,第一項是由聲波擾動帶來的影響,第二項是由熵波擾動帶來的影響.

將非等熵過程的密度擾動表達式(7)代入到線性化的質量和動量方程(6)來引入熵擾動的影響,可以得到帶源項的一維波動方程

式中,D/Dt=?/?t+/?x為物質導數.該方程具有聲類比的形式——等式左邊為描述聲傳播的波動方程,等式右邊包含由熵擾動和HR 質量擾動引起的聲源[20].顯然,熵擾動的產生將會影響聲波方程.可以看出,HR 的引入會給燃燒室帶來一個質量擾動源,該質量擾動通過方程(8)右邊的后兩項來影響燃燒室內的聲波.與此同時,HR 的存在還可能導致燃燒室內熵擾動的產生.這種方式產生的熵擾動通過方程(8)右邊的第一項也可以影響燃燒室內的聲波[21].而熵擾動具體如何影響聲波方程可通過后面推導得出的聲類比模型方程分析得出.

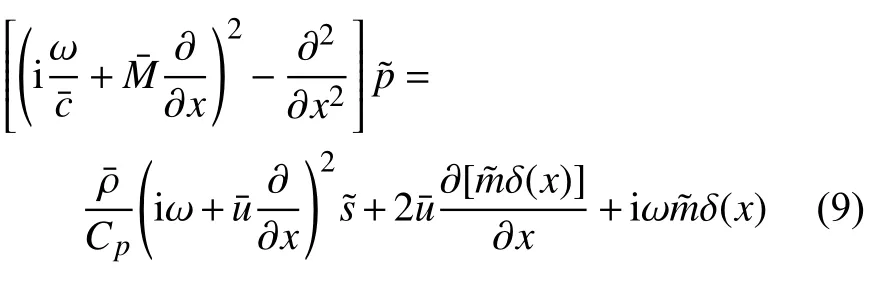
1.2 亥姆霍茲共振器模型

方程(9)右邊的質量擾動來源于共振器頸部的質量擾動,其計算可通過共振器模型與共振器入口的壓力擾動的關聯得出.在共振器頸部有平均頸流(也叫做偏流)的情況下,入射聲擾動將導致頸部穿孔邊緣非定常的渦脫落,脫落后被頸部的平均流帶走,并最終通過黏性效應耗散為流體的內能[16].穿孔頸部的聲吸收特征由瑞利導率決定[22],定義為

式中,I1,K1分別為第一類和第二類修正貝塞爾函數,為頸部的斯特勞哈爾數,rn為頸部截面的半徑,為頸部的渦對流速度,根據文獻[11,22-23],頸部的渦對流速度近似等于頸部的平均速度.

對于HR 空腔,質量守恒可以得到

式中,V為HR 空腔體積,為空腔中的平均聲速,ω為角頻率,為總的瑞利導率,由于HR 頸部內外的壓差可近似地視為頸部流體的渦流脫落和流體在頸部加速的貢獻的總和,從而頸部有限的幾何長度會帶來一個對瑞利導率的修正,修正后總的瑞利導率滿足[11,24-26]

式中,L為HR 頸部的長度.

定義HR 頸部的聲阻抗為[14]ZHR=,通過下式計算

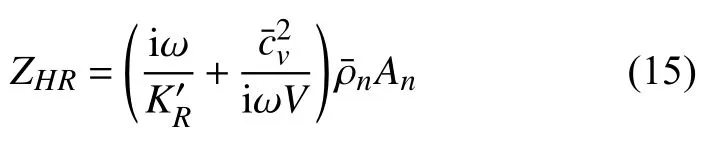
1.3 模型的解

求解頻域下聲類比模型方程(9)的解,對方程(9)來說:

(1)在x＜0 段,質量擾動源為零,熵擾動也為零;

(2)在x＞0 段,質量擾動源為零,方程右邊第一項整體也為零.

所以在這兩段,方程(9)右邊源項都為零.對于這兩段,通過轉換到頻域,偏微分方程轉化為常微分方程.解得該方程通解為

式中,k+,k-為波數,由下式計算

在0-＜x＜0+段,質量擾動源不為零.對方程(9),從 0-到 0+對x分別作一次和二次積分.可以得到

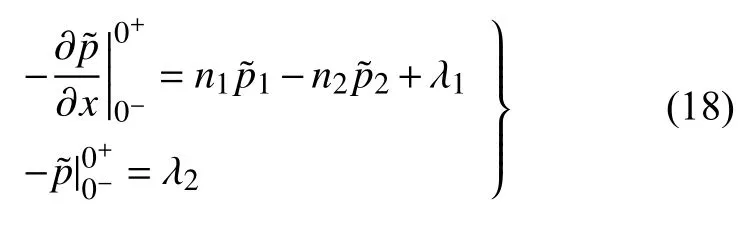
式中t1,t2,λ1,λ2可由如下式子計算

式(19)中,所有平均量已經可以在前文中求出.而HR 質量擾動也可通過線性HR 聲學模型與共振器出口壓力擾動聯系,即式(13).

為將熵擾動與HR 上、下游壓力擾動關系式求出,對方程(2)中質量和能量守恒方程作線性化,忽略一階以上的擾動,可以改寫為

將式(20)改寫,由此可以得到和其余變量之間的關系

式(21)中的可以用熱力學關系式計算

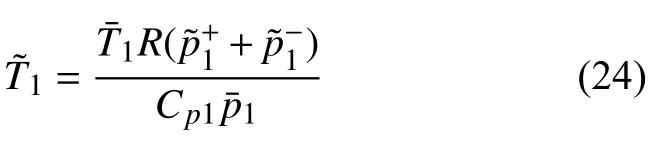
對于燃燒室中HR 上游或者下游局部,可以通過線性化后的局部質量和動量守恒[13,16]

式(21)中,可用HR 的線性模型的聲阻抗定義計算

其中

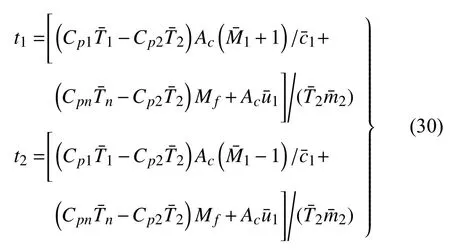
作量綱分析,t1,2中第一項與第三項的比為

將質量擾動表達式(13)代入式(18)中,可進一步減少未知數與方程組數量,得到

式中參數b1,b2,b3,b4,a1,a2如下

式(34)中,所有平均量已經可以在前文中求出.至此,只需聯立式(29)和式(33)共3 個方程,其中包含等共5 個未知數.此方程組不閉合,無法求解,故需要加入邊界條件.邊界條件一般為HR 上、下游擾動幅值,中其中2 個.由于在實際應用中,往往將亥姆霍茲共振器安裝在管道內聲波模態波峰處,以達到最佳的消聲效果,故本文中主要選取了該請況討論(給定和).對于給定上游入射聲波,并假設下游無入射聲波=0的情況,在此提供下述初步分析結果.對于給定下游入射聲波,并假設上游無入射聲波的情況,可通過相同的方程代入該邊界得到.上述后兩種情況的線性組合可得到一般聲波入射情況的解.如此未知數減少2 個,上述方程組閉合.聯立上述3 個方程可以解得的表達式,并進而可求得所有相關未知量.

2 測試與驗證

在本節中,用一個測試案列[16]來驗證上述模型,并用這個案例來說明HR 與燃燒室的溫度差是如何影響其吸聲性能的.將圓柱形亥姆茲共振器安裝于可視為一維管道的燃燒室上,如圖1 所示.測試案例中HR和燃燒室的幾何和平均流參數如表1 所示.由于模擬對象是HR 與燃燒室內局部(HR 上下游之間)的聲波和熵波關系,故不需要規定燃燒室聲學邊界條件或HR 軸向位置[16].但在本節中假設 HR 安裝在壓力波腹附近以清楚地顯示其對燃燒室聲學的影響[9,27].實際中以給定入射波,假定邊界無限長或者無反射的情況更具一般性,本文暫不考慮.

表1 HR和燃燒室的幾何與平均流參數Table 1 Geometry and mean flow parameters of the HR and combustor

2.1 等溫工況

通過方程f=c/(2π)可預測出HR 在1000 K 時的共振頻率約為535 Hz.情況一,假設HR 上游的壓力擾動幅值=100 Pa .定義熵波擾動強度幅值為,單位為Pa.其中,為熵擾動,量綱為J/(K·kg).通過所建模型繪制HR 下游壓力擾動幅值以及下游熵波擾動等關鍵參數,并對比Yang 等[16]中的假設滯止焓連續的模型和階躍條件模型的結果.如圖3(a),在HR和燃燒室等溫的情況下,在共振頻率(約535 Hz)附近時,HR 的存在會顯著影響燃燒室中共振器下游的聲波強度,但是下游溫度擾動保持不變,對共振器下游的熵波強度也基本沒有影響.可看出文中提出的聲類比模型能夠很好地匹配另外兩個模型[16]的結果.同時,這三個模型對HR 的聲吸收系數也給出了一致的預測,如圖3(c)所示.該聲吸收系數的定義為吸收能量/入射能量[28-29]

圖3 HR 溫度1000 K 時,3 個模型的壓力擾動強度幅值、溫度擾動和聲吸收系數Fig.3 The amplitude of pressure wave strength,temperature oscillationt and absorption coefficien of the three models with a HR temperature of 1000 K

2.2 不等溫工況

在HR和燃燒室不等溫的工況下.設HR 空腔冷卻氣流溫度從500 K 逐漸上升至1000 K,讓HR和燃燒室(1000 K)溫差逐漸變小,這時由于通過HR 的冷空氣流產生的擾動,HR 下游熵波強度不再約等于零.采用和等溫工況一樣的假設:=100 Pa .

通過方程f=c/(2π)可預測出HR 在500 K 時的共振頻率約為385 Hz.如圖4(a)(b)所示,500 K 時聲類比模型的對HR 下游溫度,壓力和熵波擾動強度的預測結果都與階躍條件模型的預測結果完全一致.在共振頻率(385 Hz)附近共振器下游會產生較強的熵波,而遠離共振頻率熵波強度明顯下降.HR 下游的溫度擾動也呈現出和熵波擾動一樣的趨勢,因為熵波擾動依賴于下游溫度擾動和壓力擾動.但當冷卻氣流溫度從500 K 逐漸上升至1000 K 時,階躍模型與聲類比模型的熵波擾動共振幅值將逐漸減小,直到與滯止焓模型趨于一致(趨于0).而滯止焓連續模型在任何溫度下都無法考慮HR 下游的熵擾動,故預測結果存在明顯問題.除了在經過HR 后產生熵波外,HR 的較低溫度也會導致HR 之前和之后的聲波強度之間的關系發生變化,這點可以從模型的解,圖4(a)中看出.雖然這3 個模型都預測出HR 的存在會導致向上游傳播的聲波強度加強,向下游傳播的聲波強度減弱[30-31],但聲類比模型預測的變化趨勢和要小于滯止焓模型,這與階躍條件模型結果一致,而冷卻氣流溫度從500 K 逐漸上升至1000 K 過程中,該結論任然成立.如圖4(c)所示,500 K 時聲類比模型預測的聲吸收系數的變化趨勢和峰值也要比滯止焓模型小(吸聲系數相差約100%),跟階躍條件模型一致.但當冷卻氣流溫度從500 K 逐漸上升至1000 K 時,該差異逐漸消失.由于在實際燃氣輪機和航空發動機中,總冷卻氣流可占到發動機空氣總流量的20%或以上.而此處考慮的流過共振器的平均空氣質量流量遠小于燃燒室內平均空氣流量,≈0.23% .但在共振頻率附近,共振器頸部質量流量擾動幅值與燃燒室質量流量擾動幅值為同一數量級≈26.5%,(若前者遠小于后者,則共振器無法產生顯著消聲效果).

圖43 個模型的壓力擾動強度幅值、熵波擾動強度幅值、溫度擾動和聲吸收系數Fig.4 The amplitude of pressure wave strength,enthalpy wave strength,absorption coefficient and temperature oscillation of the three models

3 結論

當帶有冷卻氣流的HR 被安裝在一維管道燃燒室上時,燃燒室中熱氣流和HR 中冷氣流的溫差需要被考慮,這將改變燃燒室內共振器上下游的聲波與熵波之間的關系,對HR 的吸聲性能和HR 對熱聲振蕩的抑制作用有顯著影響——不同的聲波關系改變了HR 的吸聲性能,而產生的熵波如果在下游被加速,則可能導致熵噪聲形式的聲波.文獻[16]基于階躍條件模型得到了HR 上、下游的聲波與熵波的關聯,可以由上游聲波與熵波代入所推導出的關系矩陣直接計算出下游的聲波與熵波,但無法看出熵波產生以及聲波關系改變的機理.本文推導了安裝有帶冷卻氣流的HR 的燃燒室中的聲類比形式的聲學模型.通過與階躍條件模型的定量比較,驗證了該聲類比模型的正確性.本模型的優點在于它是帶有源項的波動方程,從中可以直觀地看到熵擾動聲源項與共振器質量擾動聲源項的表達式,能夠區分出由熵擾動引起的聲源項和聲擾動引起的聲源項.這為理解和預測帶冷卻氣流的亥姆霍茲共振器對燃燒室熱聲振蕩的影響提供了便捷的模型.

附錄

方程組(28)和式(32) 3 個方程的求解

將上述方程組改寫成

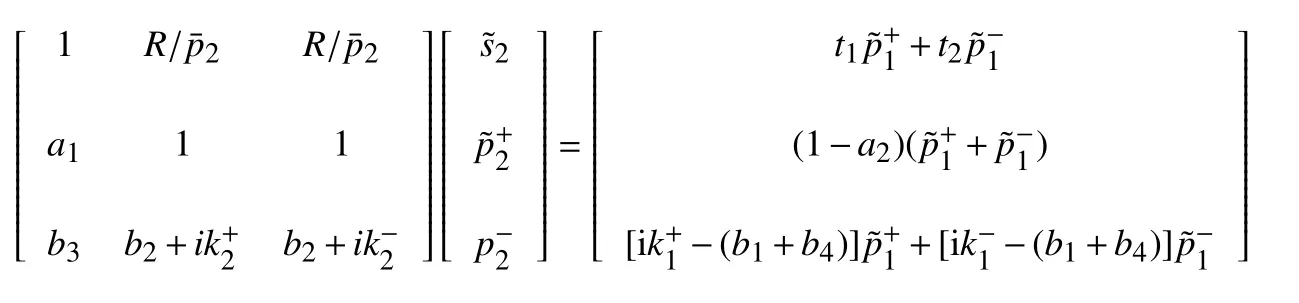
可解得