基于極限狀態法的板式無砟軌道結構檢算與優化

岳朝陽 趙坪銳 江萬紅 李秋義

1.西南交通大學土木工程學院，成都 610031；2.中國中鐵二院工程集團有限責任公司，成都 610031；3.鐵路軌道安全服役湖北省重點實驗室，武漢 430063

20世紀60年代中期，世界各國對無砟軌道的設計研究進入了一個新階段，針對不同無砟軌道結構形式提出了不同的設計方法并進行了大量試驗，取得了較大進展［1-2］。我國的CRTS系列無砟軌道充分吸收了國外無砟軌道的設計理念，根據我國鐵路建設實際情況進行了再創新和原始創新［3］，最終形成了以CRTSⅠ、CRTSⅡ、CRTSⅢ型板式軌道及CRTSⅠ、CRTSⅡ型雙塊式軌道為主的高速鐵路無砟軌道體系。CRTSⅠ型板式軌道已成功應用在哈大高速鐵路、海南東環線等線路上，顯示出較強的適應性。在再創新研究及前期日本板式軌道設計中均采用了容許應力法進行設計。為便于與國際接軌，有必要采用極限狀態法對CRTSⅠ型板式軌道結構進行驗算。

鐵路軌道設計方法正在由容許應力法向極限狀態法［4］轉變。容許應力法采用單一的安全系數，對軌道結構相應點的應力進行限制。安全系數多根據工程經驗得到，若取值不當將會影響到結構的經濟性和安全性。極限狀態法以概率統計為基礎，采用可靠度設計理念，將荷載、材料、結構與工作狀態的相關指標以分項系數的形式加以考慮，可以更好地處理結構安全性和經濟性之間的矛盾［5］。

一些學者采用極限狀態法對無砟軌道進行設計檢算。張東陽［5］采用極限狀態法對普通鋼筋混凝土CRTSⅢ型板式軌道進行了配筋優化。尹銀艷等［6］采用極限狀態法對板式軌道底座進行了配筋設計，并將設計結果與容許應力法、通用參考圖進行了對比，發現既有配筋數目可適當減少。梁爽等［7］基于極限狀態法對復合道床板進行了配筋優化。以上研究主要針對非預應力結構，對預應力結構考慮較少。CRTS 系列板式軌道在已開通的無砟軌道線路中的占比超過50%，根據極限狀態法對預應力混凝土進行優化設計具有重要的現實意義。雖然CRTS 系列軌道結構中應用了預應力結構如預應力軌道板等［8-10］，但是相應的預應力配筋設計與檢算多依據工程經驗，定性介紹內容較多，定量計算內容較少。

本文參照Q∕CR 9130—2018《鐵路軌道設計規范（極限狀態法）》，以通用參考圖為基準，對路基上CRTSⅠ型板式軌道的軌道板進行設計檢算，重點考慮預應力配筋的影響，同時對預應力軌道板的配筋檢算流程加以梳理，并根據檢算結果對配筋進行優化。配筋檢算均以全截面對稱配筋為原則。

1 結構形式及力學參數

CRTSⅠ型板式軌道結構（圖1）路基上軌道結構高度為787 mm，軌道板標準長度為4 962 mm，寬度為2 400 mm，厚度為190 mm；砂漿層厚度為50 mm；底座板厚度為300 mm，寬度為3 000 mm［11］。扣件垂向剛度為50 kN∕mm，地基面剛度為76 MPa∕m。其他主要力學參數見表1。

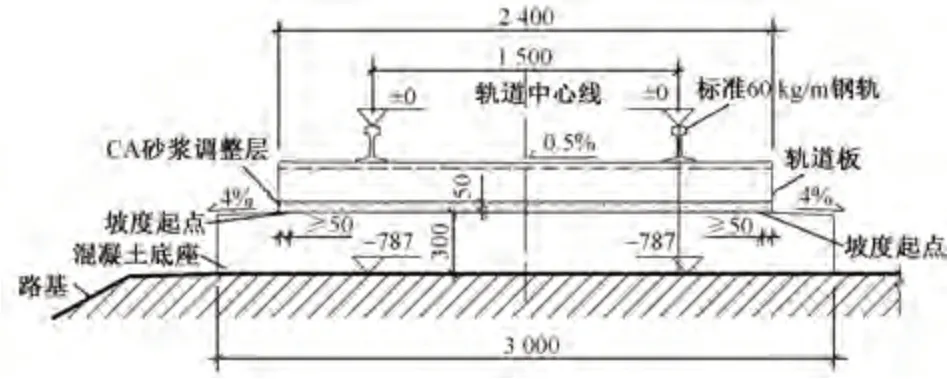
圖1 CRTSⅠ型板式軌道結構（單位：mm）

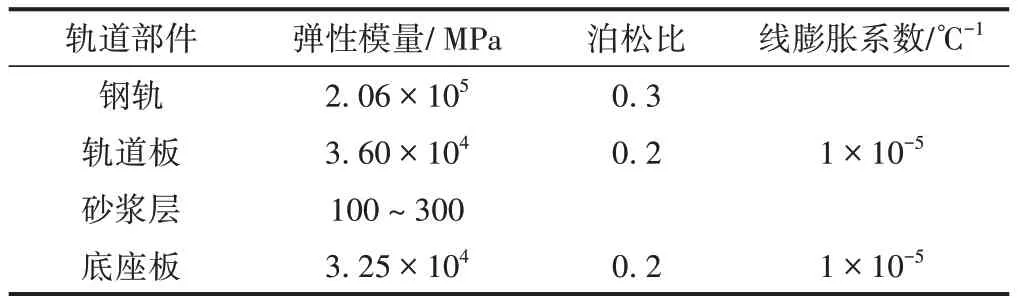
表1 CRTSⅠ型板式軌道結構主要力學參數

2 荷載效應計算

2.1 列車豎向荷載

列車豎向荷載作用下的軌道板彎矩采用梁板模型（圖2）計算得到，其中鋼軌選用梁結構來模擬，軌道板、底座選用薄板結構來模擬，扣件、砂漿層、地基選用彈簧結構來模擬［12］。參照Q∕CR 9130—2018，列車豎向荷載標準值取2P（P為靜輪重）。計算得到單位長度軌道板縱向正、負彎矩分別為14.73、1.85 kN·m，橫向正、負彎矩分別為11.50、0.81 kN·m。

圖2 CRTSⅠ型板式軌道有限元模型

2.2 列車橫向荷載

參照Q∕CR 9130—2018，列車橫向荷載標準值取0.8P，即68 kN。列車橫向荷載作用下的軌道板橫向彎矩Mh計算公式為

式中：Q為列車橫向標準荷載；h為軌道板頂面至鋼軌頂面的距離。

計算可得，列車橫向荷載作用下，單位長度軌道板橫向彎矩為0.89 kN·m。

2.3 溫度梯度

軌道結構在外界溫度變化時會產生溫度梯度現象，從而產生翹曲彎矩。根據TB 10082—2017《鐵路軌道設計規范》，正溫度梯度（上熱下冷）取90 ℃∕m，負溫度梯度（上冷下熱）取45 ℃∕m。板厚修正系數取1.08。參照Q∕CR 9130—2018，溫度梯度作用下的軌道板彎矩Mtdk計算公式為

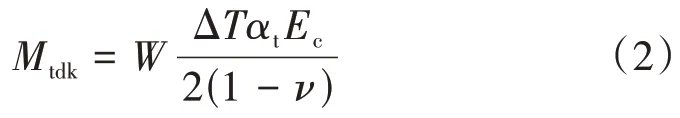
式中：W為彎曲截面系數；ΔT為軌道板上下表面溫差；αt、Ec、ν分別為軌道板混凝土的線膨脹系數、彈性模量、泊松比。

計算可得，溫度梯度作用下，單位長度軌道板縱向正、負彎矩分別為25.00、12.50 kN·m，橫向正、負彎矩分別為25.00、12.50 kN·m。

2.4 路基不均勻沉降

路基不均勻沉降的形狀取半波余弦型曲面，取每20 m 不均勻沉降15 mm。路基不均勻沉降所引起的軌道板基礎變形作用彎矩Mcjk的計算公式為

式中：EI為軌道板抗彎剛度；κ為基礎變形曲線曲率，分別為基礎變形的變形幅值和波長。

計算可得，路基不均勻沉降所引起的單位長度軌道板縱向彎矩為7.61 kN·m。

3 荷載作用效應組合

根據Q∕CR 9130—2018，承載能力極限狀態分為基本組合和偶然組合，分別按式（4）和式（5）計算承載能力極限狀態軌道板的荷載作用效應組合彎矩M。

式中：Mdk為列車荷載彎矩標準值；γd為分項系數，取1.5；ψtd為組合系數，取0.5；γtd為分項系數，取1.0；Mnqk為梁體撓曲變形作用彎矩標準值；γnq為分項系數，取1.0（在路基段中本項不納入計算，下同）。

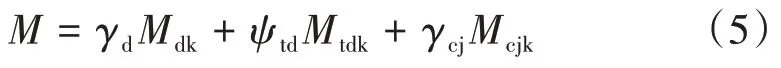
式中：γd為分項系數，取1.0；ψtd為準永久值系數，取0.5；γcj為分項系數，取1.0。

承載能力極限狀態單位長度軌道板的荷載作用效應組合彎矩計算結果見表2。可以看出，縱向正負彎矩受偶然組合的控制，橫向正負彎矩受基本組合的控制。

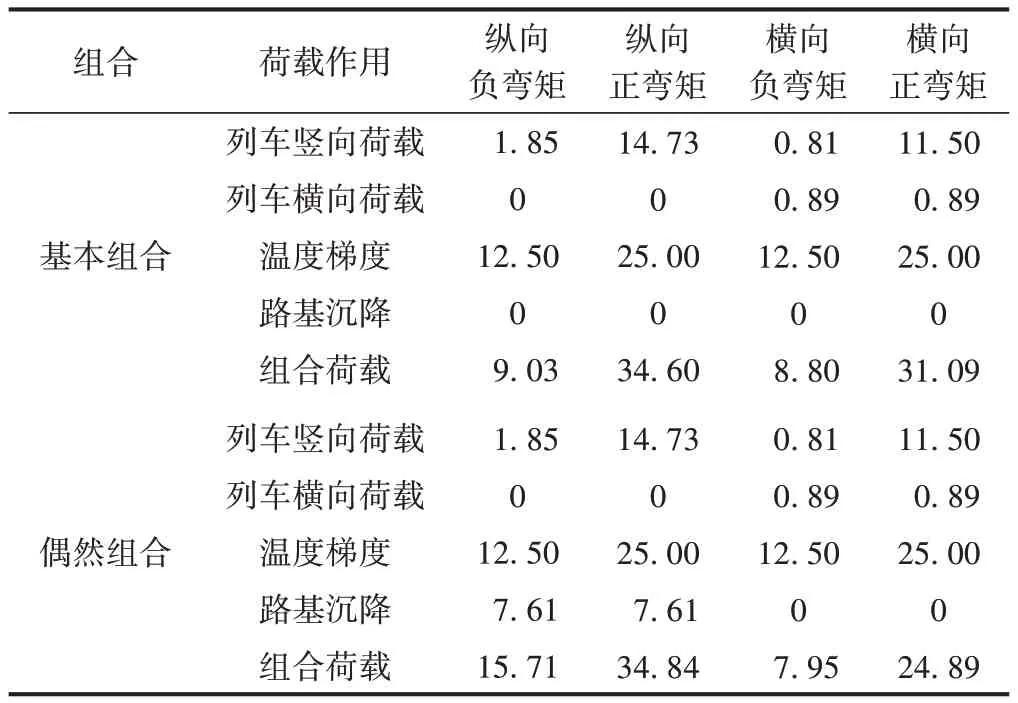
表2 承載能力極限狀態單位長度軌道板的荷載作用效應組合彎矩計算結果 kN·m

正常使用極限狀態分為標準組合、頻遇組合和準永久組合，配筋驗算中利用標準組合進行計算。根據上述各荷載作用效應計算正常使用極限狀態軌道板的荷載作用效應標準組合彎矩MQ，表達式為

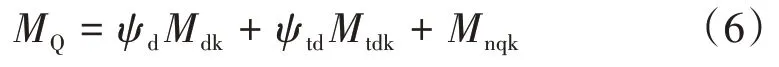
式中：ψd為組合系數，取0.75；ψtd為組合系數，取0.5。

標準組合下，正常使用極限狀態單位長度軌道板的荷載作用效應組合彎矩計算結果見表3。

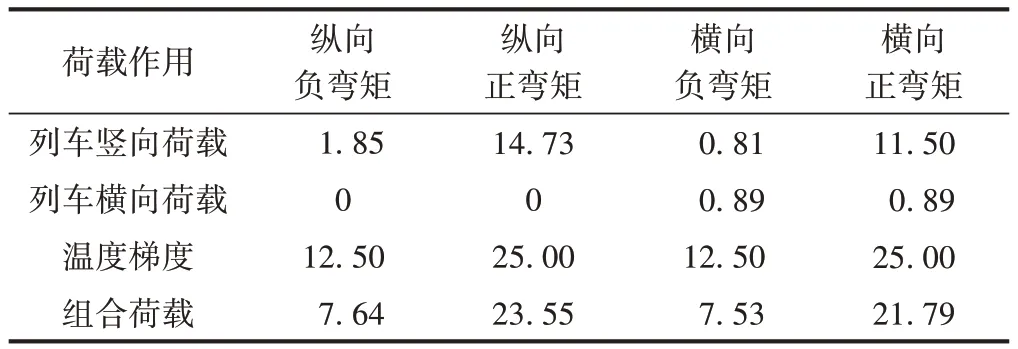
表3 正常使用極限狀態單位長度軌道板的荷載作用效應組合彎矩計算結果 kN·m

4 配筋驗算

4.1 材料參數

采用等級為HRB335、直徑為12 mm 的環氧樹脂鋼筋，抗拉、抗壓強度設計值均為300 MPa；預應力鋼筋采用直徑為13 mm 的無黏結預應力鋼棒，屈服強度標準值為1 420 MPa。C60 混凝土抗壓、抗拉強度設計值分別為27.50、2.04 MPa，軸心抗拉強度標準值為2.85 MPa。配筋情況見圖3，考慮對稱性，左側為預應力鋼筋，右側為普通鋼筋。下文均采用單位長度軌道板的彎矩進行計算。

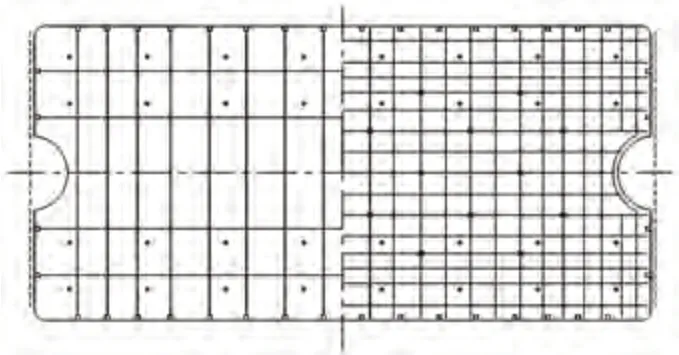
圖3 CRTSⅠ型軌道板鋼筋布置

4.2 承載能力極限狀態配筋檢算

參照Q∕CR 9130—2018，承載能力極限狀態下軌道板作用彎矩應滿足

式中：γ0為結構重要性系數，正線無砟軌道取1.0；MR為軌道板彎矩抗力。

如圖4 所示，將軌道板視為預應力混凝土矩形截面構件，其正截面承載力計算見式（8）—式（10）。

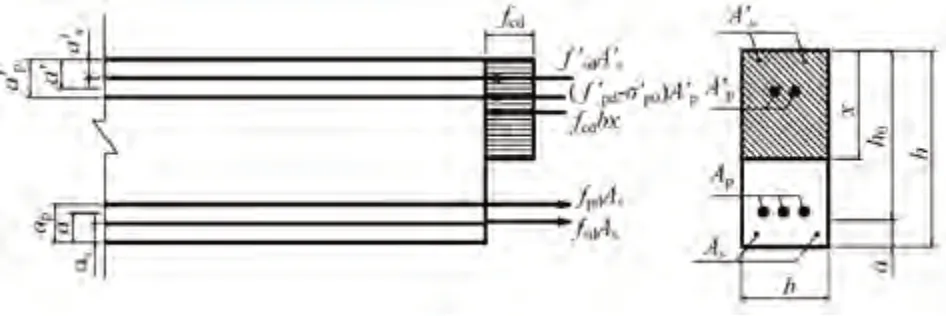
圖4 預應力混凝土正截面承載力計算示意

由于配筋采用對稱布置，縱向正彎矩起控制作用，因此以縱向下層配筋為例進行計算。縱向下層配置4 根無黏結預應力鋼棒，距截面邊緣63 mm；15 根HRB335 普通鋼筋，距截面邊緣48 mm。將相關數據代入式（8）—式（10），計算可得：x =17.4 mm ＜ξh0=53.6 mm，MR=60.05 kN·m ＞γ0M=34.60 kN·m，其中ξ為相對受壓區高度系數。可知，承載力滿足要求。由于采取對稱配筋，可知縱向上層配筋也滿足要求。

類似地，對橫向下層配筋進行計算。橫向中性軸處配置16 根無黏結預應力鋼棒，距截面邊緣95 mm；28 根HRB335 普通鋼筋，距截面邊緣36 mm。將相關數據代入式（8）—式（10）計算可得：x =25.6 mm ＜ξh0=49.8 mm，MR=78.71 kN·m ＞γ0M=31.09 kN·m。可知，承載力滿足要求。由于采取對稱配筋，可知橫向上層配筋也滿足要求。

4.3 正常使用極限狀態配筋檢算

參照Q∕CR 9130—2018，預應力混凝土結構的正常使用極限狀態須進行受拉邊緣應力或截面裂縫寬度的檢算。對預應力混凝土結構，在荷載標準組合下，受拉邊緣應力應滿足

式中：σck為作用標準組合下抗裂檢算邊緣的混凝土法向應力；σpc為扣除全部預應力損失后在抗裂檢算邊緣混凝土的預壓應力；ftk為混凝土軸心抗拉強度標準值。

無開裂時，處于彈性工作狀態的軌道板邊緣法向應力表達式為

根據相關規范，張拉控制應力σcon取0.50fpyk～0.85fpyk（fpyk為屈服強度標準值），計算時取0.70fpyk，同時預應力損失取0.4σcon，與文獻［13］較為吻合。軌道板邊緣混凝土預壓應力計算公式為

式中：Np為構件預加力；An為靜截面面積；epn為預加力作用點至靜截面重心的距離；In為靜截面慣性矩；yn為計算處至靜截面重心的距離；σp2為由預應力次應力所引起的法向應力。

以縱向下層配筋為例進行檢算。計算可得σck=3.91 MPa，σpc= 1.40 MPa。σck-σpc= 2.51 MPa ＜ftk=2.85 MPa，檢算合格。

類似地，對橫向下層配筋進行檢算。計算可得σck=3.62 MPa，σpc=1.34 MPa。σck-σpc=2.28 MPa ＜ftk=2.85 MPa，檢算合格。

5 配筋優化

由承載能力極限狀態與正常使用極限狀態的檢算可知，既有設計均滿足規范要求和構造要求。針對承載能力極限狀態，無論是縱向下層還是橫向下層，其正截面承載力均有較大富余量，與正截面承載力的比值分別為42.4%和60.5%。對結構配筋起控制作用的是正常使用極限狀態，縱向下層與橫向下層混凝土邊緣拉應力均未超限，但富余量較小，與抗拉強度標準值的比值分別為11.9%和20.0%。

正常使用極限狀態下軌道板縱向下層、橫向下層預應力鋼筋數量與混凝土邊緣拉應力的關系見圖5。可知：預應力鋼筋數量與混凝土邊緣拉應力呈線性關系；縱向下層配置3 根預應力鋼筋時軌道板正截面邊緣拉應力不滿足要求，縱向下層配置4 根預應力鋼筋時已達到最優，無需再優化；當橫向下層配置9根預應力鋼筋時混凝土邊緣拉應力才超過限值，因此通用參考圖的設計具有較大富余量。綜上，對于荷載較小、速度較低的軌道來說，可以在滿足最小配筋率的前提下適當降低橫向預應力配筋數量，提高經濟性。

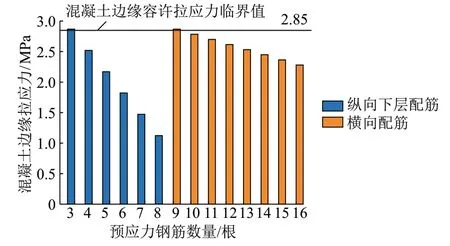
圖5 正常使用極限狀態下軌道板預應力鋼筋數量與混凝土邊緣拉應力的關系

在承受正彎矩的預應力結構中，預應力鋼筋一般布置在受拉區，從而充分發揮抵消荷載拉應力的作用。偏心距越大，預加力越大，則抵消效果越好。但是對于軌道板結構，其截面高度較其他工程結構小，預加應力過大可能會在軌道板上層造成拉應力過大的現象從而發展成裂縫，因此在軌道板中布置的預應力鋼筋均靠近截面中部，從而預應力鋼筋的作用會在一定程度上被減弱。即使如此，通用參考圖的配置仍然滿足要求，而且在橫向上還有較大富余量。可以看出容許應力法與極限狀態法相比是較為保守的，采用極限狀態法對結構進行設計和檢算擁有較優的可行性與經濟性。

6 結論

1）承載能力極限狀態下，基于通用參考圖進行驗算，軌道板橫向正、負彎矩受基本組合控制，縱向正、負彎矩受偶然組合控制，其正截面承載力均滿足規范要求。

2）正常使用極限狀態下進行標準組合的驗算，軌道板混凝土受拉邊緣應力均滿足規范要求。

3）承載能力極限狀態下，軌道板正截面承載力均有較大富余量，配筋數量受標準組合控制。縱向配筋數量已達最優，橫向配筋數量富余較大，可以根據線路狀況適當減少，最多可降低37.5%。