大型沉井基礎長期位移規律及對全橋影響分析

施洲 周勇聰 江峰 呂大財 鐘永新 潘永杰

1.西南交通大學土木工程學院，成都 610031；2.中國鐵路上海局集團有限公司南京鐵路樞紐工程建設指部，南京 200142；3.中交第二航務工程局有限公司，武漢 430040；4.中國鐵道科學研究院集團有限公司鐵道建筑研究所，北京 100081

沉井基礎具有承載力大、整體性好、抗船撞能力強、抗震性好、不需額外施工平臺等優點［1］，常作為大跨度橋梁橋塔、錨碇等結構的基礎。隨著沉井基礎面積不斷增大，在施工下沉過程中摩阻力及就位后的長期位移更為復雜。

文獻［2］基于離心機模型試驗研究沉井基礎井外側壁摩阻力的分布形式，發現沉井沉入土體的外側壁摩阻力從地表至沉井底部呈先增大后減小的近似拋物線分布趨勢。文獻［3］運用仿真分析和現場試驗對沉井初沉階段的受力特性及開裂特性進行研究，分析沉井采用大鍋底、中鍋底、小鍋底等下沉方式時沉井底部的變形和應力范圍。文獻［4］基于某沉井基礎側壁摩阻力的現場測試結果，研究沉井入土深度引起土體松弛高度對井壁摩阻力沿高度分布的影響，發現沉井在下沉就位后的受力與長期變形對橋梁的影響顯著。文獻［5］通過假定基底摩擦力遵循庫倫摩擦定律，采用Winkler 模型計算沉井基底豎向土反力和井身水平土反力，推導了沉井水平位移計算公式和滑移臨界荷載公式。文獻［6］采用分層總和法和離心機模型試驗對常泰長江大橋沉井基礎的沉降量進行了預測，二者得到的預測值基本相同。文獻［7］根據現場沉降監測數據和有限元模型分析了施工過程中的鸚鵡洲長江大橋沉井應力分布與變形情況以及施工對鄰近建筑物的影響，發現沉井在下沉過程中部分沉井結構有較大拉應力出現，且周圍土體的沉降量隨沉井下沉深度的增大而增大。文獻［8］利用有限元軟件建立了五峰山長江大橋沉井基礎與鄰近地基的數值模型，結合現場監測數據較準確地預測了沉井基礎和鄰近樁基的沉降、水平位移。文獻［9］基于模型試驗對軟土中的沉井基礎在長期水平荷載作用下的變形特征進行了研究，發現隨著時間的增加，沉井的變位仍會增大。文獻［10］通過數值模型預測雙沉井下沉時地表沉降和徑向位移的關系，并對比了雙沉井采用非同步下沉、交替下沉和同步下沉三種方案引起的地表沉降，發現采用同步下沉對地表沉降影響最小。文獻［11］根據現場檢測數據和數值模擬揭示了軟土地基中沉井突沉的實質是應力突變引起應變能向損傷耗散能的瞬間轉化。

連鎮鐵路五峰山長江大橋為主跨1 092 m 的公鐵兩用懸索橋，北錨碇沉井基礎是國內第一個長度超過100 m 的沉井基礎，也是體積最大的沉井基礎［12］，其工后及運營期間的長期變形直接影響大橋的線形與受力，甚至影響高速列車的運營。本文基于Winkler 模型和分層總和法理論預測工后階段沉井的變位，并利用數值模擬分析沉井長期變位對大橋的影響。

1 沉井工程概況

五峰山長江大橋為連鎮鐵路上跨越長江的橋梁，主橋為雙塔連續鋼桁梁公鐵兩用懸索橋，橋跨布置為（84+84+1 092+84+84）m，見圖1。橋梁上層為雙向8 車道一級公路，設計速度 100 km∕h，下層為4 線客運專線，設計速度250 km∕h。

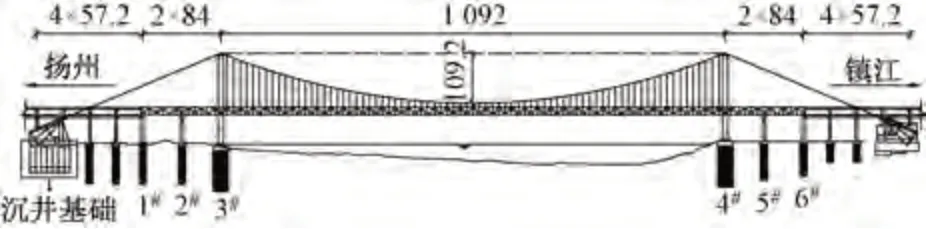
圖1 主橋立面布置（單位：m）

大橋的北錨碇采用100.7 m（長）×72.1 m（寬）的大型矩形沉井基礎。沉井外壁厚2.0 m，內隔墻厚1.3 m，平面設置了48個10.9 m（長）×10.2 m（寬）的矩形井孔。沉井高56 m，共分10 節，首節為鋼殼混凝土沉井，高8 m，底部設有高1.8 m、踏面寬0.2 m 的刃腳；剩下的9 節為鋼筋混凝土沉井，其中第2 節高6 m，第3節到第8節每節高5 m，第9節高4 m，第10節高8 m。沉井封底混凝土厚12 m。沉井頂面標高為+1.0 m，基底標高為-55.0 m，基底置于粉細砂層。沉井頂蓋是一個長69.7 m、寬98.3 m、厚6～8 m 的鋼筋混凝土頂蓋。沉井結構見圖2。

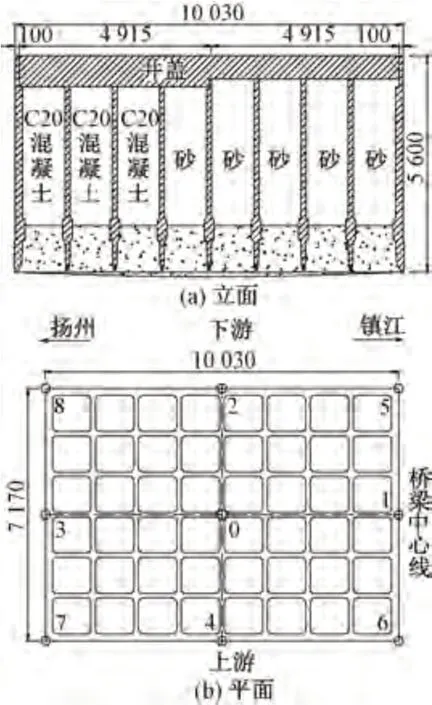
圖2 北錨碇沉井立面與平面布置（單位：cm）

沉井基礎位置主要為淤泥土、淤泥質粉質黏土、粉砂、粉細沙等，下伏基巖為石英閃長斑巖，基巖頂面標高在-63.7～-54.6 m。各類土體特性參數見表1。其中，*表示采用砂樁加固的土層。

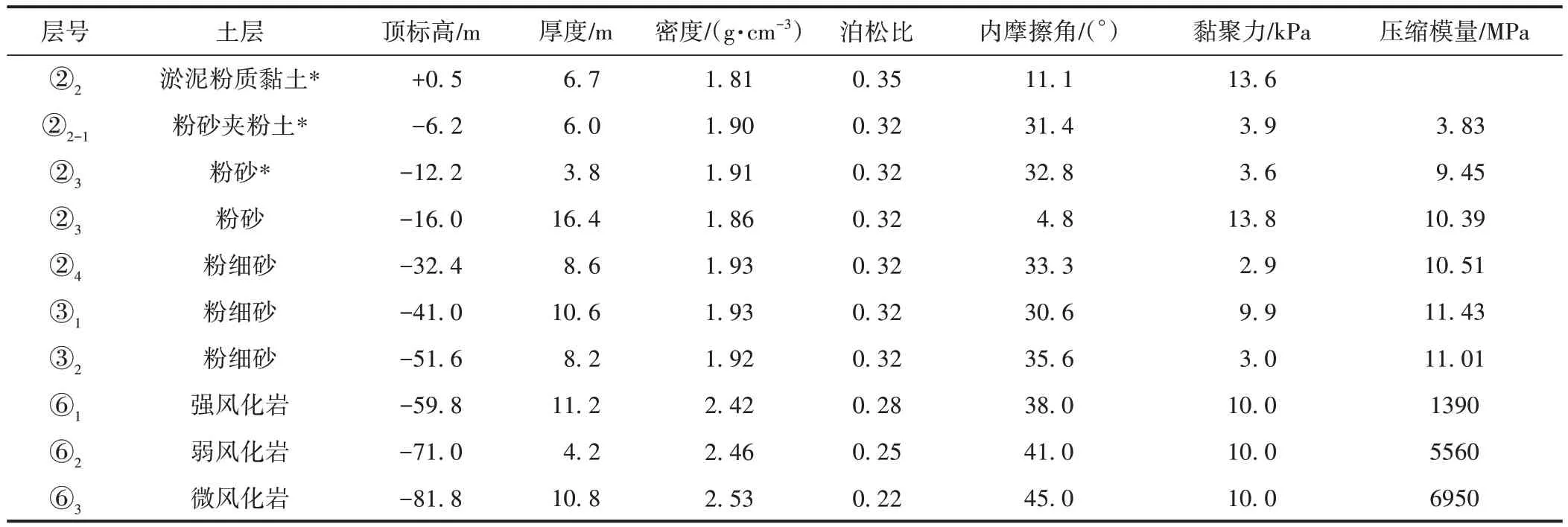
表1 北錨碇沉井典型地層分布

沉井采用三次分段施工及下沉的方案。首次施工前3 節，采用排水和十字槽開挖工藝下沉至標高-8.0 m。第2次施工第4節—第6節，采用水下吸泥和不排水工藝下沉至標高-30.0 m，從標高-8.0 m 下沉至-15.0 m 時采用8 區開挖，從標高-15.0 m 下沉至標高-30.0 m 時采用4 區開挖；第3 次施工第7 節—第10 節，先采用中部核心土支撐的工藝從標高-30.0 m下沉至-45.0 m，最后使用不排水和大鍋底開挖的工藝從標高-45.0 m下沉至標高-55.0 m。沉井就位封底后，遠離主橋的18個井孔填充C20水下混凝土，靠近主橋的12個井孔填充清水，其余中部18個井孔填充砂。

2 施工監測與工后沉降分析

2.1 沉井下沉施工過程監測結果與分析

為了獲得沉井在下沉施工過程中的下沉量、沉井平面位置等幾何參數，在沉井的4個角點、沉井外壁的中部和沉井中心設置了人工測量測點，測點布置參見圖2。沉井下沉開始后，第1 次下沉用時49 d；第2 次下沉用時42 d；第3 次下沉用時45 d。取各測點平均下沉量繪制下沉曲線，見圖3。

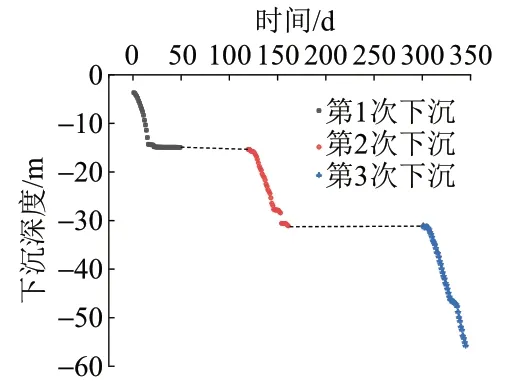
圖3 沉井施工下沉曲線

由圖3 可知：沉井首次降排水下沉累計下沉了14.937 m，平均下沉速度為0.305 m∕d，最大下沉速度達到1.503 m∕d。第2次累計下沉了16.148 m，穿過的土層有粉砂、粉質黏土夾粉土、黏土層等，平均下沉速度為0.385 m∕d，在第2 次下沉過程后期，沉井發生了多次突沉；第3次下沉累計下沉了24.614 m，穿過的土層有粉砂、粉細砂，雖然下沉阻力較大，但因采用了空氣幕、大直徑吸泥機等助沉措施，有效控制了沉井的下沉速度，平均下沉速度為0.547 m∕d。

2.2 工后沉降監測結果與分析

在沉井就位后依次進行沉井內填充，沉井基礎上的錨碇、橋墩、主纜錨固塊等結構施工，用時866 d。在此期間對沉井沉降量進行連續監測，在沉井下沉就位后的54 d 內每日監測，其后每隔7 ～ 10 d 進行監測。工后沉井各測點累計沉降量見圖4。可見，沉井就位后各測點的累積下沉量為12.2 ～ 22.9 cm，各測點的平均下沉量為17.4 cm，說明在后續施工影響下沉井沉降量較為顯著且存在一定不均勻性。沉井靠近長江一側（鎮江側）的1、5 和6 號測點的下沉量和下沉速度基本一致，并且下沉速度經歷了由快到慢，再由慢到快的一個過程。沉井另外一側的3、7 和8 號測點的下沉量和下沉速度基本一致，并且下沉速度經歷了由快到慢的變化過程；累計下沉量在工后650～866 d 發生反向增長的情況。沉井就位后的前650 d，3、7 和8 號測點的下沉量大于1、5 和6 號測點的下沉量，這是因為靠近3、7 和8 號測點一側的井孔填充了混凝土，而靠近1、5 和6 號測點一側的井孔填充了水和砂石，后者重量小于前者。沉井就位后的650 ～ 866 d，1、5 和 6 號測點的下沉量增大，3、7 和 8 號測點下沉量為負值，這是因為安裝主纜后，主纜巨大的拉力造成沉井揚州側微小上升。

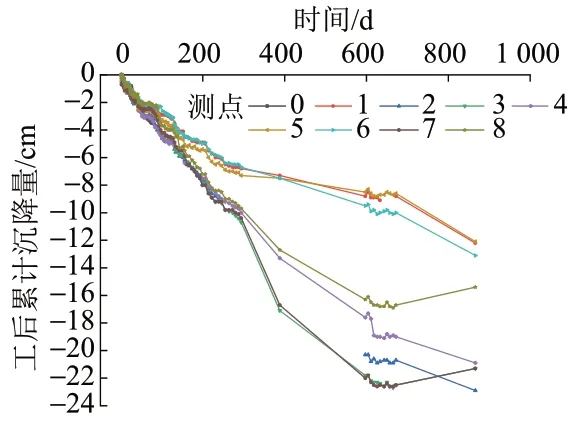
圖4 工后沉井各測點累計沉降量

將各次監測得到的沉井下沉增量除以與前一次監測的時間間隔得到兩次監測時間段內的平均沉降速度，見圖5。可知，沉井的沉降速度曲線總體呈先減小后增大最終趨于穩定的發展趨勢，最終沉井的下沉速度為0.006 7 cm∕d，說明沉井已經基本穩定。

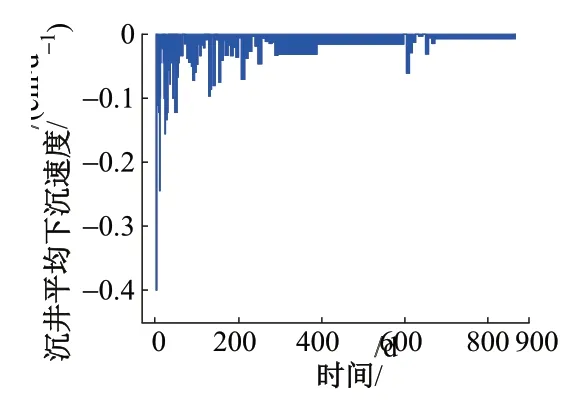
圖5 沉井工后每天平均下沉速度

3 運營期沉井長期位移預測與分析

3.1 沉井長期位移理論分析

3.1.1 沉井長期水平位移預測

大橋運營后的沉井長期水平變位受多種因素影響，計算的理論模型也有很多，其中基于Winkler 模型的計算理論應用較多。文獻［5］根據沉井與地基連接面的位移協調條件，推導出矩形沉井在地表截面處受水平荷載F、彎矩M、豎向力N、自重G聯合作用下滑移判別公式和沉井水平位移計算公式。

滑移判別公式為

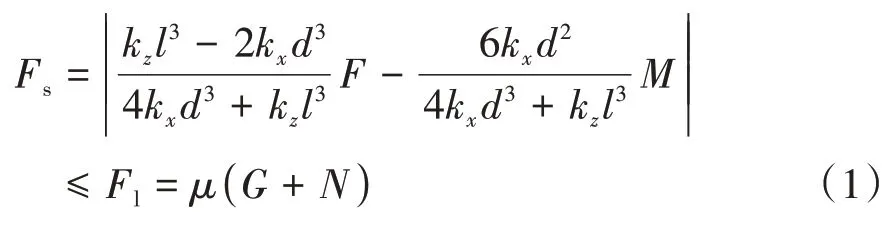
式中：Fs為滑移力；Fl為臨界荷載；l、b、d分別為沉井的長度、寬度和埋深；kx為水平地基反力系數；kz為豎向地基反力系數；μ為基底摩擦因數。

當基底無滑移時，沉井頂部水平位移ut為

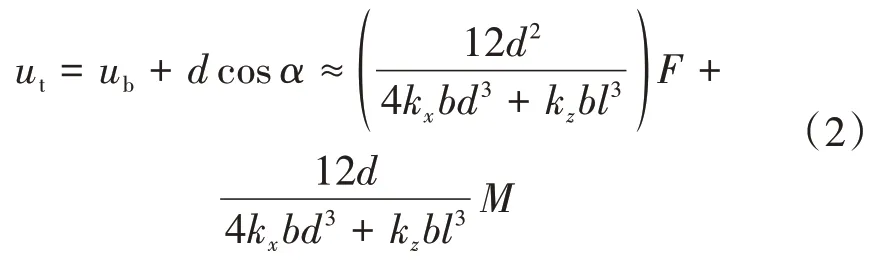
式中：ub為沉井底部水平位移；α為沉井轉角。

當基底滑移時，沉井頂部水平位移ut為

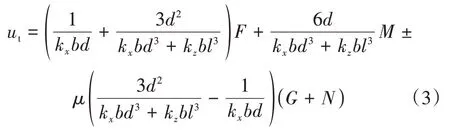
五峰山長江大橋沉井整個基礎自重約13 GN，運營階段主纜拉力取1.8 GN，邊跨纜索與水平夾角為36°，M=0，μ=0.3，kz取（2.0～4.0）× 104kN∕m3。按傳統的彈性模型方法計算得到kz=5kx。根據式（1）計算出Fs為23 840 MN，小于Fl的32 650 MN，可見沉井不會發生滑移。

將沉井及周圍土體參數代入式（2）得到基底不滑移水平位移為1.485～2.971 cm，參考JTG D65T-05—2015《公路懸索橋設計規范》中錨碇基礎頂部主纜的水平位移不得大于橋梁中塔間距的L∕10 000（L為主跨跨徑），即10.920 cm，可見大橋沉井基礎的長期水平位移較小。

3.1.2 沉井長期豎向沉降預測

選擇分層總和法計算沉井基礎沉降量S，即

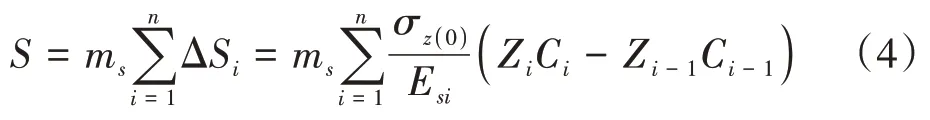
式中：ms為沉降經驗修正系數；ΔSi為第i層土的沉降量；n為劃分的土層數目；σz（0）為基底附加應力；Esi第i層土的壓縮模量；Ci、Ci-1均為平均附加應力系數；Zi、Zi-1分別為基底至第i和第i-1層底面的距離。

將沉井基礎的參數帶入式（4），計算得出沉井錨碇的豎向沉降量為2.643 cm，參考JTG D65T-05—2015 規范中運營階段錨碇的沉降量不大于0.000 2L的要求，即21.84 cm，可見沉井的沉降量相對較小。另外，考慮沉井錨碇上有N3、N4 兩個橋墩，參考TB 10093—2017《鐵路橋涵地基和基礎設計規范》中墩臺均勻沉降限值3 cm，可知沉井錨碇上的橋墩沉降量在容許范圍內。

3.2 長期變位數值模擬

為進一步分析沉井基礎的長期位移，采用Plaxis-3d 有限元軟件模擬錨碇在主纜拉力作用下的變形情況。建立500 m（長）×500 m（寬）×150 m（高）的土體模型，沉井模型和錨體模型均按照實際尺寸1∶1 建立。模型土體底部固結，側面對稱約束，沉井與土體單元共用節點。沉井采用C30 混凝土，錨體采用C35 混凝土，錨體建模時考慮前側空室。土體選擇摩爾庫倫模型，土體材料參數按照表1中密度、壓縮模量等參數取值，沉井及錨體材料按照TB 10002—2017《鐵路橋涵設計規范》參數取值。模型荷載主要考慮土體、沉井、錨體等自重及運營期主纜力。運營階段錨碇豎向和縱橋向位移見圖6。可知：錨碇縱橋向最大水平位移1.577 cm，與Winkler 模型計算的水平位移1.485 ～2.971 cm接近；最大沉降量為2.913 cm，與分層總和法計算的沉降量2.643 cm 接近。表明基于Winkler 模型的計算結果與有限元分析結果吻合良好。

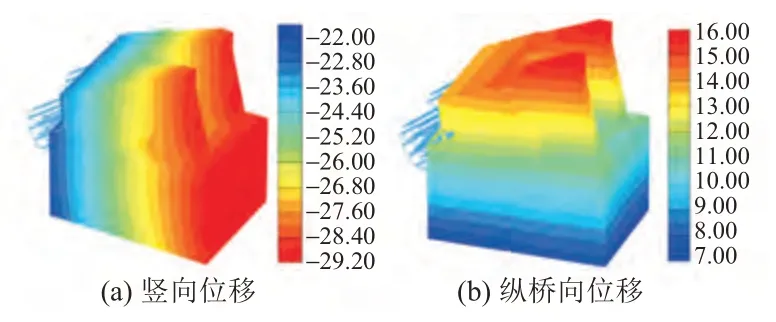
圖6 運營階段錨碇豎向和縱橋向位移（單位：mm）

4 沉井長期位移對大橋的影響分析

4.1 沉井位移對錨碇上橋墩的影響分析

大橋沉井基礎上設置了引橋的2個橋墩N3、N4（圖7）。橋墩隨沉井的沉降、平移、轉動同步變形，進而引起梁體高程發生變化，影響高速鐵路軌道標高及線形。當沉井轉動時，84 m 高的橋墩會放大墩頂的水平與豎向位移，加劇墩頂主梁的標高變化，對高速鐵路線形長期變形的影響更顯著。

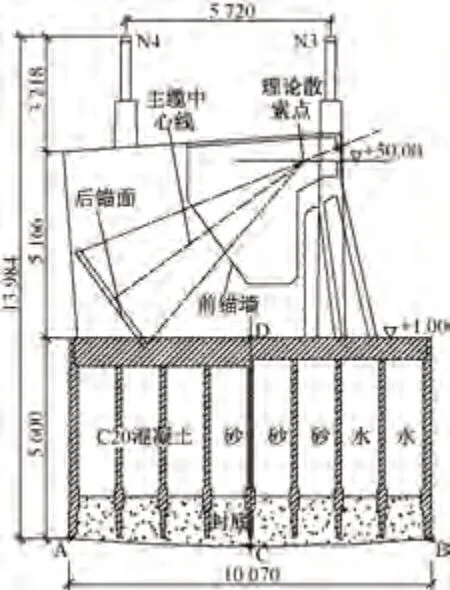
圖7 錨碇沉井立面（單位：cm）

TB 10093—2017 規定，對于有砟軌道，相鄰墩臺基礎工后沉降差應小于15 mm。因此，假定N3、N4 墩頂由于沉井轉動導致的沉降量差值為15 mm，計算沉井和錨碇分別繞A、B、C 或D 點發生順時針剛體轉動的角度限值θc，進而計算此時N3、N4 橋墩的水平位移H3和H4，具體結果見表 2。其中，L3、L4分別為轉動中心到N3、N4墩頂的距離；θ3、θ4為轉動中心與N3、N4墩頂連線和鉛垂線的夾角。可知，雖然假設沉井繞不同轉動中心轉動，但根據墩頂沉降量差值計算得到的轉角θc均為 0.015°。N3、N4 墩最大水平位移H3和H4分別為3.78、3.67 cm，明顯小于該跨跨徑57.20 m 采用伸縮裝置的縱橋向最大位移±60 mm，可見N3、N4墩的水平位移并不顯著。

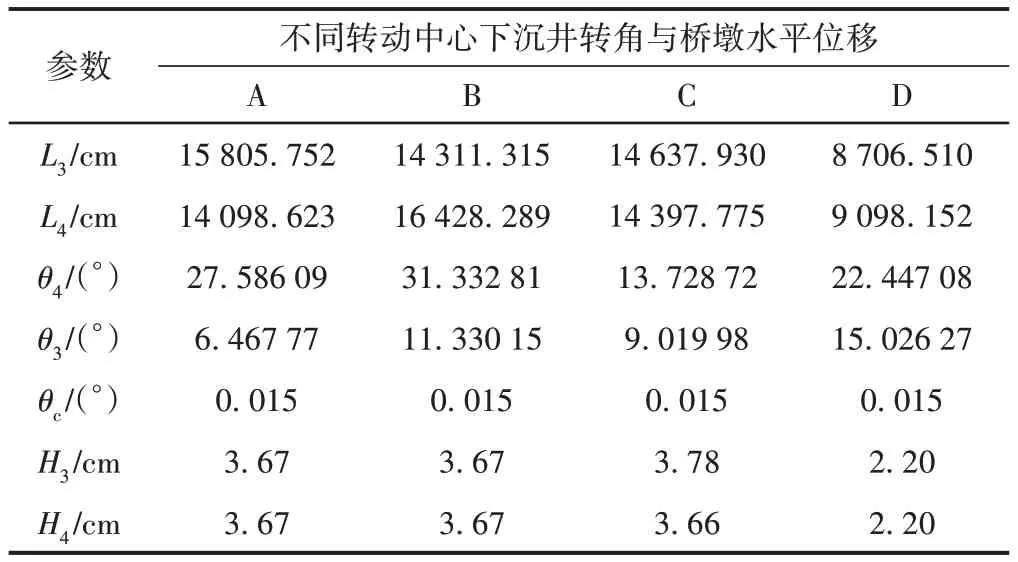
表2 N3、N4墩沉降差為15 mm時沉井轉角與橋墩水平位移

4.2 沉井基礎長期位移對主梁線形的影響分析

運營階段錨碇變位會引起主纜及主梁線形發生變化。假定沉井基礎分別發生1 cm 的水平位移u、沉降v后，計算得到主梁各控制截面的豎向位移；另外，將沉井位移預測計算分析得到的最大水平位移2.971 cm、沉降2.913 cm 分別代入有限元模型敏感性分析矩陣，得到主梁各控制截面的豎向位移，見表3。沉井長期水平位移及沉降對主梁線形的影響曲線見圖8。

表3 沉井水平位移及沉降引起主梁豎向位移 cm

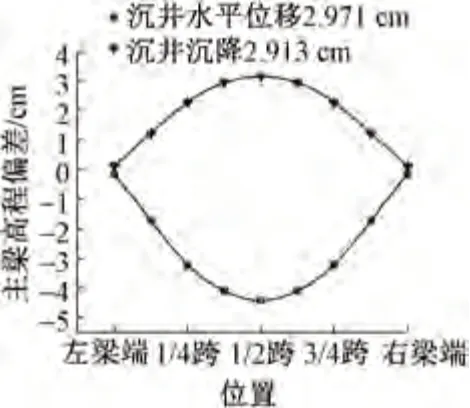
圖8 沉井長期水平位移及沉降對主梁線形的影響曲線

由表3 和圖8 可知，主梁線形變化沿跨中對稱分布，并且沉井水平位移及沉降對跨中主梁的豎向位移影響最大。當沉井水平位移為2.971 cm 時，主梁跨中下撓 4.427 cm，對應撓跨比為 1∕24 468；沉井下沉2.913 cm 時，主梁跨中上撓3.146 cm，對應撓跨比為1∕34 710，即沉井水平位移對主梁線形的影響稍大于沉降的影響。沉井水平位移為2.971 cm 時，主梁撓跨比 1∕24 468 僅為五峰山大橋撓跨比限值 1∕400［13］（列車和汽車共同作用時）的1.5%，可見沉井長期位移對于主梁線形的影響較小。

5 結論

1）沉井下沉就位后的866 d 中，各測點發生了12.1 ～ 22.9 cm 的沉降，沉降速度曲線總體呈先減小后增大最終趨于穩定的發展趨勢，最終沉井的平均下沉速度僅為0.0067 cm∕d，表明沉井已經穩定。

2）基于Winkler 模型理論計算表明沉井在運營期間不會發生滑移，計算出沉井基礎在運營期的長期水平位移為1.485 ～ 2.971 cm；利用分層總和法計算出沉井的沉降為2.643 cm；利用數值模擬計算結果得到的縱橋向最大水平位移、沉降分別為1.577、2.913 cm，與理論值接近，均小于規范限值。

3）根據沉井上 N3、N4 橋墩沉降差限值 15 mm 推導出沉井工后轉動角度限值為0.015°，對應N3、N4 墩最大水平位移分別為3.78、3.67 cm，其量值明顯小于該跨伸縮裝置最大位移量±60 mm。

4）沉井水平位移對主梁線形的影響稍大于沉降的影響，沉井水平位移為2.971 cm 時主梁線形撓跨比是規范限值的1.5%，表明沉井長期位移對主梁的線形影響較小。