云制造環境下考慮不確定性的產品配置優化

李 嘉,楊 東

(東華大學 管理學院,上海 200051)

云制造是在“制造即服務”的理念上,利用云計算技術為生產企業提供了一種低成本、網絡化和全球化的制造服務,從而實現生產從大規模模式轉向面向用戶的個性化服務模式[1-2]。根據Einpresswire發布的統計數據,2018年全球云制造市場規模為387億美元,預計到2024年全球云制造市場規模將增長至1 190億美元。而2019 年國內云計算市場規模也達到了1 382億元。典型的國內云制造平臺有海爾公司的COSMOPlat 云制造平臺、中國航天的“航天云網CASICloud”以及富士康工業互聯網平臺BEACON。隨著制造業標準化和通用化的提高,現代制造企業已從單一的產品制造轉向多個制造商分部件或分工序協作完成。因而,越來越多的企業開始轉向云制造模式,從而實現產品和零部件的生產和制造。產品配置作為實現個性化定制的主要技術之一,可以利用云制造技術實現其對客戶的個性化配置[3]。

產品配置是實現大規模定制的主要技術之一[4-5]。在大規模定制下,產品被設計成由實現了產品功能的各種模塊所組成,而模塊又分為共性模塊、變型模塊和可選模塊等[6]。通過對這些模塊的選擇和組合,從而實現了對顧客個性化的配置[7]。傳統上產品配置的研究主要都假定模塊的生產制造均由本企業完成,因而其研究主要關注于如何獲得一個可行的配置。所采用的方法是應用人工智能中的問題求解技術,包括基于規則的推理[8]、基于實例的推理[9]以及基于約束滿足的方法[10]。然而,隨著產品變型及其模塊實例個數實例的增加,產品配置被當成一個優化問題[11-12]。Aldanondo 等[11]采用整數規劃的方法建立產品配置優化模型,從而獲得最優的配置。Dou等[12]采用交互式的遺傳算法來優化顧客協同參與的產品配置。Badurdeen等[13]考慮產品模塊的可回收性,從產品生命周期的可持續性角度出發,采用多目標優化遺傳算法NSGA_II來優化產品配置決策。此外,隨著全球供應鏈網絡的興起,一些學者將產品配置的研究和供應鏈管理的研究相結合,從而借助于供應鏈網絡來實現產品模塊的定制和生產。Khalaf等[14]提出將模塊的制造由供應鏈上的制造廠來完成,其優化目標是最小化供應鏈總的成本,并建立了供應鏈環境下的混合整數規劃模型。Yang等[15]提出將產品設計者和模塊供應鏈看成是博弈決策的雙方,產品設計者決策目的是最小化總的產品設計和制造成本,而供應鏈決策者的目標是最小化總的供應鏈成本,并提出了基于博弈論的決策優化方法。盡管基于供應鏈的產品模塊定制提供了一種借助供應鏈上下游企業來實現模塊生產和產品配置的方法,但供應鏈上下游企業屬于一種緊耦合的狀態,因而供應鏈下產品配置的優化目標通常是最小化供應鏈的總成本,包括模塊的制造成本、設施的選址成本、庫存管理和物流成本。與之對照,云制造是一種通過云服務的方式實現了產品模塊化的定制,主企業和云制造商屬于一種服務和被服務的方式,主企業只需支付云制造服務費用就實現模塊的交付,而無需考慮云制造商的庫存管理和設施選址等問題,屬于一種松耦合的方式。

但是,上述研究都假定所有的參數都是確定的。在實際場景中,模塊的制造成本、制造提前期都受市場、供應鏈的不穩定性等因素而不可避免地出現波動。因此,如何處理產品配置問題中的不確定性已引起研究人員的重視[16-20]。目前,主要有兩種處理產品配置中不確定性的方法,即模糊數法和隨機規劃方法。Liu等[18]采用模糊數學的方法來表示產品模塊提前期的不確定性,基于模糊表達的提前期采用多目標模糊優化方法進行產品配置模塊的決策。文獻[19-20]中考慮模塊部件的提前期不確定性,提出采用隨機規劃的方法來建模不確定情況下的產品配置優化問題,從而可以用隨機規劃的算法(如Benders分解方法)來求解產品配置優化問題。然而,上述兩種方法都存在一定的不足。基于模糊數的方法過于依賴主觀因素,而基于隨機規劃的方法都假定參數的變化服從一定的概率分布。這一假設過于嚴格,因為實際中企業很難準確估計這些參數的概率分布。

魯棒優化作為處理不確定性的優化方法[21],并不要求事先知道不確定參數的概率分布,它著力于優化在最壞情況下的目標值。因此,魯棒優化適合于求解現實問題中參數概率分布難以準確估計的優化問題。Soyster[22]首次提出了魯棒優化的概念來求解線性規劃中的不確定性。隨后,Ben-Tal等[21]提出了參數的不確定集分別為區間和橢球的魯棒優化方法。然而,基于區間不確定集的魯棒優化在實際中過于保守,因為它假定所有參數的最壞情形會同時發生。盡管基于橢球不確定集的魯棒優化能夠避免這種情況,但其魯棒等價模型屬于二階錐規劃,存在難于處理和求解等問題。針對基于區間和橢球魯棒優化方法的不足,Bertsimas等[23]進一步提出了基于budget的魯棒優化方法,它通過budget控制參數來調節魯棒最優性和約束違背之間的關系,從而使得決策者可以根據自己的風險意識來平衡決策的保守性和目標的最優性。此外,基于budget的魯棒優化由于其等價模型也屬于線性規劃模型,因而具有模型易于處理性和可解性等優點,已廣泛應用于各種魯棒優化問題的求解中。自從魯棒優化問世以來,研究學者已將魯棒優化應用于應急服務設施選址、呼叫中心的運營安排、供應鏈網絡設計等包含不確定性的優化問題中。孫華麗等[24]考慮了需求不確定性和運輸時間不確定性下的應急設施選址和路徑的魯棒優化。邱若臻等[25]擴展了報童模型,研究了需求參數的不確定集分別為區間和橢球情況下的多市場魯棒優化模型。于淼等[26]針對呼叫中心實際運營中顧客到達不確定性的特點,采用魯棒離散優化方法,建立呼叫中心人員配置的魯棒優化模型。彭春等[27]考慮了各應急醫療服務站點的需求不確定性,分別構建了區間、橢球和多面體不確定集,比較了在這些不確定集下的應急醫療服務站魯棒選址決策方案。于冬梅等[28]同時考慮了需求不確定性和設施毀壞情景,建立了服務能力有限情況下的可靠性設施選址魯棒優化模型。張夢玲等[29]針對應急救災情況下的資源配置優化,提出了不確定需求下考慮供應商參與的兩階段魯棒優化模型。Baron等[30]考慮具有多個周期下的設施選址問題,提出了采用區間和橢球不確定集來刻畫需求的不確定性,并建立了相應的魯棒優化模型。Alem 等[31]研究了家具行業的生產計劃,并考慮了生產成本和需求的不確定性,建立了基于budget的魯棒優化模型。Zokaee等[32]提出采用魯棒優化的方法來優化供應鏈設計,并考慮了需求、供應鏈產能和運輸成本的不確定性,以面包供應鏈為例闡述了該方法的有效性。Lu等[33]研究了顧客需求不確定下的車輛路徑問題,建立了基于budget的魯棒優化模型,并開發了相應的分支-定價算法來求解該優化模型。

綜上所述,魯棒優化是處理優化問題中的不確定性的有效方法。針對現有產品配置研究的不足,考慮到云制造商的制造數據(如云制造成本和時間)的概率分布由于數據稀少或者企業數據保密問題難以精確獲取,而云制造數據區間(即上下界)相對容易獲得,故采用可調節的魯棒優化方法研究云制造環境下的產品配置魯棒優化問題,并考慮模塊的云制造成本和云制造時間的不確定性。采用基于budget的區間不確定集來刻畫云制造成本和云制造時間的不確定性,并建立了相應的魯棒優化模型。通過對偶理論,將其轉化為魯棒線性等價模型。采用一個配置案例闡述了所提出的魯棒優化方法的有效性,并進行了魯棒控制參數、擾動比例的靈敏度分析。最后,采用蒙特卡洛仿真方法對魯棒解進行數值實驗,從而證明了魯棒優化模型比確定性模型相比,具有能夠保證約束滿足、改進產品的交貨期、魯棒解更為穩定等優點。

1 模型描述

1.1 問題敘述

某大規模定制企業采用了基于模塊化的產品結構,即一個產品由實現了不同功能的多個模塊所組成,包括共性模塊、變型模塊和可選模塊。而變型模塊又有多個可候選的模塊實例,這些模塊實例在產品性能、價格方面略有差異,從而體現了產品的差異化,以滿足不同顧客的需求。同一模塊的模塊實例是“多選一”關系,即XOR(Exclusive OR)關系,配置時只能從中選擇一個實例。此外,模塊之間存在各種配置規則,包括互斥規則、條件選擇規則等。其中,互斥規則是指兩個模塊的模塊實例不能存在于相同的配置中。而條件選擇規則是指如果選擇一個模塊實例,則必須選擇另一個模塊實例。由于云制造具有成本低廉、制造效率高、無需購買專用設備和一次性固定投資等優點,因而該定制企業采用云制造模式進行各種模塊的制造和生產,即本企業只負責模塊的配置設計,而模塊的制造均由提供各個制造任務的云制造商所完成。由于云制造網絡環境下制造任務的復雜性和多樣性,模塊的云制造成本和云制造時間具有不確定性,因而云制造環境下的產品配置問題就是如何在制造成本和制造提前期不確定的情況下,在保證顧客需求和配置規則的前提下,確定產品的模塊配置方案,從而使得總的配置成本最小。

根據產品配置的特點,做出如下假設:

(1)由于共性模塊在所有的產品中必須進行選擇,它們并不影響配置決策結果,因而在配置決策中并不考慮。

(2)顧客需求通常表現為對產品功能或性能的需求。由于根據產品的設計特性,存在從功能域到物理域(模塊)的映射關系,因而根據映射關系,顧客需求可以簡化為對產品模塊的選擇要求。

(3)模塊的制造均采用云制造的方式,主企業只負責模塊的設計。并假定已完成云制造商的選擇和匹配決策,因而每個模塊的云制造商是已知的。

(4)模塊的制造任務是順序進行,只有前一個模塊完成后,后一個模塊的制造任務才能開始。但制造任務的排序是已知和給定的,因而本問題并不研究云制造任務的排序。

1.2 符號說明

建立優化模型時,將使用一些符合表示集合、參數、決策變量等,其中,“～”表示參數是不確定參數,如

集合及符號:

I——顧客訂單的集合,i∈I

J——模塊的集合,j,j＇∈J

K——模塊實例的集合,k,k＇∈K

Uc——參數的不確定集合

Ut——參數的不確定集合

XORj——模塊j的“多選一”候選實例集合

INC——互斥規則集合,(jk)∈INC

SEL——條件選擇規則集合,(jk)∈SEL

CR——顧客需求表達的集合,rijk∈CR

jk——模塊j的第k個實例

參數:

ACjk——模塊實例jk的裝配成本

——模塊實例jk的云制造成本

ATjk——模塊實例jk的組裝時間

——模塊實例jk的云制造時間

uj——產品中所包含的模塊j個數

rijk——顧客i對模塊實例jk的要求(=1,表示顧客選擇該模塊實例;=0,表示顧客不選擇該模塊實例)

DTi——訂單i的交付時間

ai——訂單i的產品數量

決策變量

xijk——對于訂單i,是否選擇模塊實例jk(=1,選擇;=0,否)

1.3 模型建立

根據上述參數和符號,建立如下不確定情況下的產品配置模型(P):

在模型(P)中,式(1)為目標函數,即配置總成本,它包括所有模塊的配置設計成本和模塊的云制造成本。其優化目標是最小化最差情況下的配置總成本,即Min-max問題。式(2)表示隸屬于同一模塊的可候選模塊實例之間的XOR 關系,即只能從該模塊的所有候選模塊實例中選擇一個。式(3)、(4)表示兩種不同類型的配置規則,即互斥規則和條件選擇規則。其中,式(3)為互斥規則,即一個模塊實例和另一個模塊實例不能同時選擇在一個產品中。式(4)為條件選擇規則,即如果選擇一個模塊實例,則必須選擇另一個模塊實例;反之,則不成立。式(5)為產品的交付期限制,即產品的生產總時間要滿足顧客對該產品交付期的要求,其總生產時間包括模塊的云制造時間和模塊的配置設計時間。式(6)為顧客對模塊的選擇要求。式(7)為0-1整數變量約束。

2 魯棒優化處理

由于模塊的云制造成本、云制造時間存在不確定性,如果采用隨機規劃等方法,則存在著其分布函數難以估計、概率難以獲取等問題。而魯棒優化作為一種處理不確定性優化的方法,它主要關注在最差情況下的最優值,并不要求對不確定參數的分布函數或概率做出嚴格的估計。基于區間的魯棒優化僅僅要求不確定參數在一個區間內取值。這對實際問題而言,獲取每個參數的區間范圍是相對容易的。因此,采用基于budget的區間魯棒優化的方法處理云制造成本和時間的不確定性。

2.1 云制造成本的不確定性處理

其中,cjk和為云制造成本的名義值和最大偏離值。引入budget控制變量Γ1,其目的是根據決策者的風險意識來調整參數的變動個數,從而調整模型的魯棒性和最優性。其含義是不可能所有參數的不確定性都同時發生,最多可能有Γ1個參數發生變化、且另一參數其值改變(Γ1-Γ1。引入集合J1={(j,k)＞0}表示具有不確定變化的參數下標集合。由于產品配置中模塊具有XOR 結構,故Γ1的取值為區間為[0,|J|],其取值可以為整數或實數。

根據目標函數中包含不確定參數的魯棒優化處理方法,對于目標表達式(1),引入變量η,則目標函數等價于:

式(9)包含不確定參數,根據其不確定集Uc的定義,可以轉化為

由于制造成本的魯棒budget控制系數為Γ1,引入保護函數β(Y,Γ1),則式(10)的魯棒表達可以寫為

式中,

定理1式(10)等價于如下線性優化問題:

證明觀察β(Y,Γ1)表示的極值問題采用基于集合的表達方法,它表示從集合J1中選取Γ1個參數,其取值為1;而從集合中選取剩下的一個參數,其取值為(Γ1-Γ1)。引入[0,1]區間的實數決策變量Yjk,以表示是否從該集合中選取或部分選取該參數cjk。顯然,β(Y,Γ1)也可以用如下線性規劃模型表示:

根據對偶理論,模型式(13)的對偶問題可以表示為:

式中,變量ρ、λjk分別為與原問題模型式(13)中第1條和第2條約束相對應的對偶變量。根據強對偶理論,原問題模型式(13)和對偶問題模型式(14)的最優目標值是相等的。因此,將模型式(14)代入式(11)中的β(Y,Γ1)可得模型式(12),問題得證。

2.2 云制造時間的不確定性處理

模型(P)中式(5)包含云制造時間的不確定變量,定義其取值范圍為即～T的不確定集

其中:Tjk為名義值;為最大偏離值。引入budget控制變量Γ2,令集合J2={(j,k)＞0}表示具有不確定變化的參數下標集合。由于產品配置中模塊具有XOR 結構,故Γ2的取值區間為[0,|J|],其取值可以為整數或實數。

參照魯棒優化模型約束右邊存在不確定變量的轉化方法,根據其不確定集Ut的定義,式(5)可以轉化為

由于云制造時間的budget控制系數為Γ2,引入保護函數Ψi(T,Γ2),故式(15)的魯棒表達可以寫為

式中,Ψi(T,Γ2)是保護函數,令其等于:

定理2式(15)等價于如下線性優化問題:

證明觀察Ψi(T,Γ2)所表示的極值問題采用基于集合的表達方法,它表示從集合J2中選取Γ2個參數,其取值為1;而從集合中選取剩下的一個參數,其取值為(Γ2-Γ2)。引入[0,1]區間的實數決策變量Zjk,以表示是否從該集合中選取或部分選取該參數～Tjk。顯然,Ψi(T,Γ2)可以用如下線性規劃模型表示:

根據對偶理論,模型式(18)的對偶問題可以表示為:

式中,變量ρi、σijk分別為與原問題模型式(18)中的第1條和第2條約束相對應的對偶變量。根據強對偶理論,原問題模型式(18)和對偶問題模型式(19)的最優目標值是相等的。因此,將模型式(19)代入式(16),問題得證。

根據定理1和定理2,同時考慮模塊的云制造成本和時間不確定性,產品配置模型(P)的魯棒優化等價模型(P_RO)為:

該模型中,如果令Γ1=Γ2=0,則魯棒優化模型(P_RO)變為確定性的產品配置模型(P);如果令Γ1=Γ2=|J|,則變為基于區間的魯棒優化模型。由于魯棒優化模型(P_RO)是一個線性規劃模型,故用商業求解器(如CPLEX)對模型進行求解。

3 案例分析

某制造企業采用基于模塊的產品設計,從而便于實現對客戶的個性化配置。該產品由7個功能模塊(A、B、C、D、E、F、G)組成(見表1),分別實現了產品的不同功能特性。而每個模塊又提供了兩個可候選的模塊實例,體現在產品性能或價格差異化的特征,以滿足客戶個性化的需求。例如,模塊A 具有兩個候選的模塊實例A1和A2,配置時只能從中選擇一個。該企業采用了云制造生產模式,即這些模塊的制造均云制造給制造商,本企業只負責模塊的配置設計。由于云制造生產任務的多樣性和復雜性,因而存在著云制造任務成本和時間的不確定性。表1給出了云制造不確定成本以及時間的名義成本和名義時間。表2、3分別給出了產品的配置規則和顧客的配置要求。

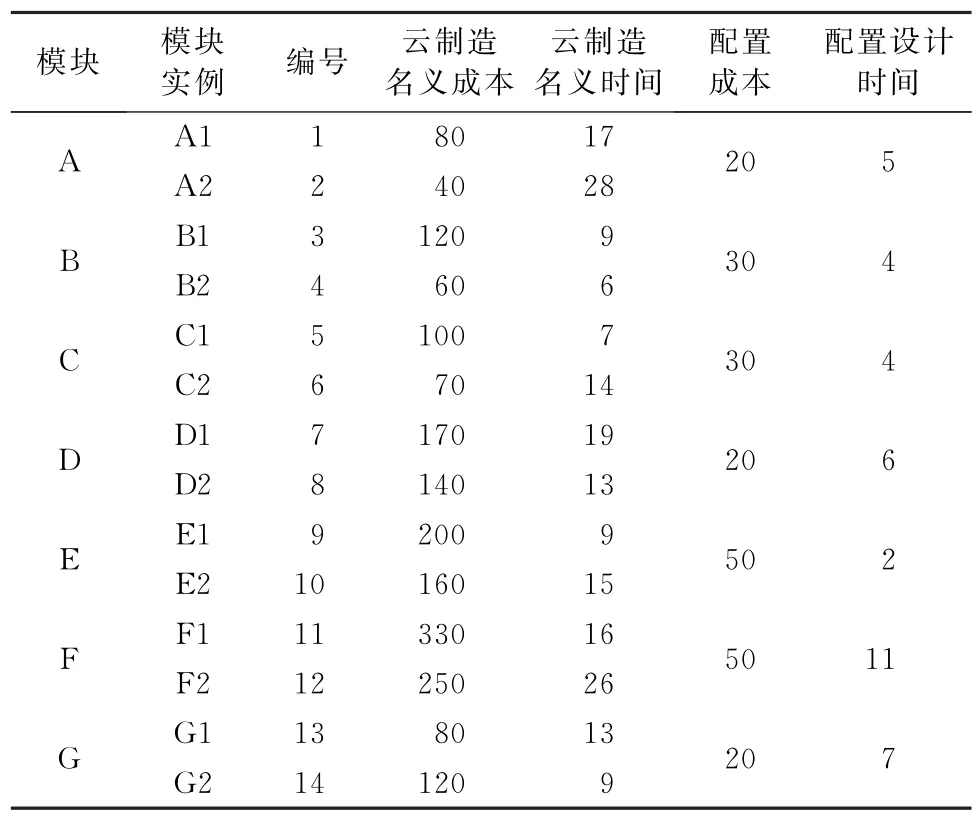
表1 產品的模塊構成及名義數據

表2 產品配置規則

由表3可以看出,為簡化計算,假設顧客訂單數量為1,顧客指定要求選擇模塊G1。此外,顧客要求的交貨期為1 540 h。

表3 顧客需求

3.1 不確定性對產品配置的影響

(1)云制造成本的不確定性。將上述參數代入模型(P_RO)采用CPLEX 求解,并令Γ2=0,χ2=0。表4給出了當擾動幅度χ1為80%、魯棒控制參數Γ1取不同值時的產品配置結果。Γ1=0即為確定模型的解。

由表4可以看出,魯棒模型的配置總成本要高于確定模型的配置總成本。隨著控制參數Γ1的增大,決策者越來越傾向于保守和謹慎,為了應對不確定性的風險,魯棒成本也不斷增加。此外,隨著魯棒控制參數Γ1的取值不同,模塊的配置結果也發生改變。例如,當Γ1=2,配置結果為選擇模塊編號為1、3、6、8、10、12和13的模塊實例,即(1,3,6,8,10,12,13),對應的模塊為A(1)—B(1)—C(2)—E(2)—F(2)—G(1)。即模塊A,B,G 均選擇其第1個實例,模塊C,D,F均選擇其第2個實例。當Γ1=4,配置結果為(1,4,6,8,9,12,13),即對應的模塊為A(1)—B(2)—C(2)—E(1)—F(2)—G(1)。與Γ1=2時的配置結果相比較,其區別在于Γ1=4時的配置結果中模塊實例B 選擇了實例2,模塊E 選擇了實例1;Γ1=2時模塊B選擇了實例1,模塊E選擇了實例2。其原因是,模塊B(1)和E(2)的擾動成本(名義成本的80%)大于模塊B(2)和E(1)的擾動成本,如果Γ1=4時仍然選擇B(1)和E(2),將會導致約束式(9)不能滿足,所以Γ1=4時選擇了擾動成本更低的B(2)和E(1)。此外,在某些情況下,Γ1值的改變并不會導致配置結果的改變。例如Γ1=2和Γ1=3時的配置結果并沒有發生改變,這是因為Γ1=2配置中模塊的擾動量能夠滿足Γ1=3時保護函數的要求,即對于約束式(9),Γ1=2配置結果仍有足夠的保護值(保護函數β(Y,Γ1)取值),從而使得約束式(9)而不違例。圖1所示為Γ1取值分別為2、4和6時的模塊實例選擇結果。

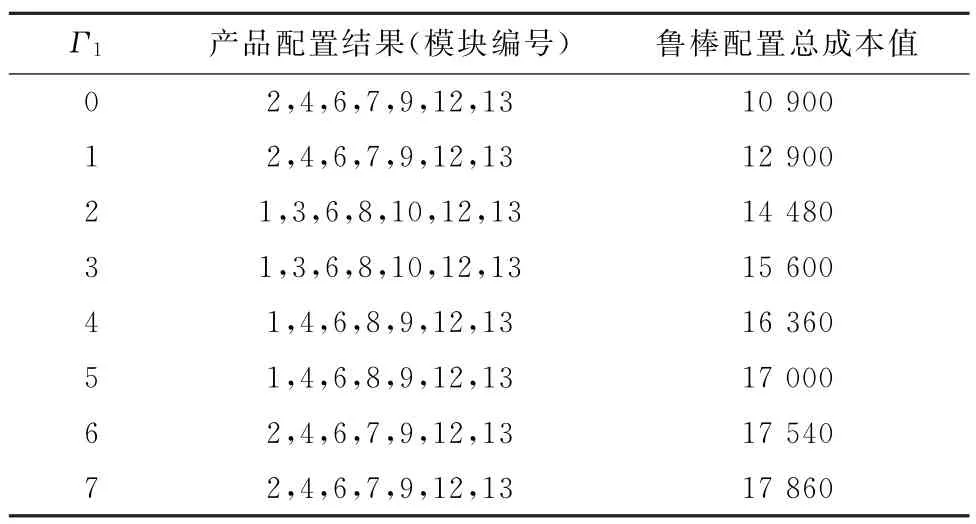
表4 擾動幅度χ1=0.8下的模塊配置結果

(2)云制造時間的不確定性。為更好地研究云制造時間的不確定性對產品配置結果的影響,令Γ1=0,χ1=0,即不存在云制造成本的不確定性。將上述參數代入模型(P_RO)并采用CPLEX進行求解,擾動比例為0.3 情況下的產品配置結果如表5所示。其中,Γ2=0即為確定模型下的配置解。

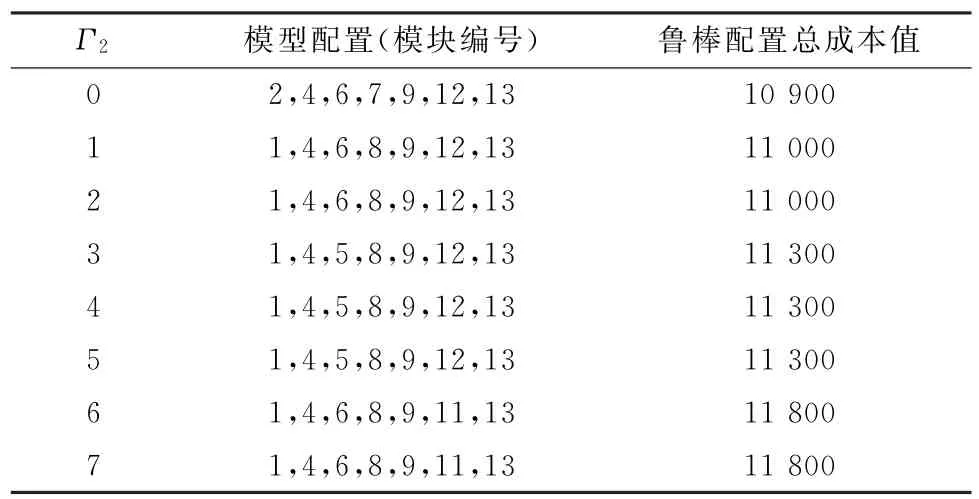
表5 擾動幅度χ2=0.3下的模塊配置結果

由表5可以看出,魯棒配置總成本高于確定模型下的配置成本。此外,隨著魯棒控制參數Γ2的增加,模塊的總的配置成本也不斷增加。其原因是,隨著Γ2的增加,表示擾動的模塊個數越多、總的制造時間不確定性增大。為應對這種不確定性,滿足產品交付期的限制,將選擇成本高、但制造時間較短的模塊,從而導致總成本的增加。例如,在Γ2=4時的配置結果為(1,4,5,8,9,12,13),即A(1)—B(2)—C(1)—D(2)—E(1)—F(2)—G(1)。在Γ2=6時的配置結果為(1,4,6,8,9,11,13),即A(1)—B(2)—C(2)—D(1)—E(1)—F(2)—G(1)。兩者的區別在于前者選擇了模塊C(1)和F(2),而后者選擇了模塊C(2)和F(1),其余模塊選擇均相同。這是因為模塊C(1)和F(2)的云制造時間的擾動值(名義值的20%)比模塊C(2)和F(1)的云制造擾動值更大,會導致約束式(5)不能滿足,所以當Γ2=6時,將選擇擾動值更小、但制造成本更高的模塊C(2),從而導致配置總成本的增加。圖2所示為Γ2取值為2、4和6時的模塊實例配置結果。

3.2 擾動比例的影響

進一步分析不確定參數的擾動比例對配置結果的影響。擾動比例χ1和χ2分別為20%、40%、60%、80%和100%。對于模塊云制造成本的不確定性,圖3所示為在不同擾動比例下目標函數(配置總成本)隨魯棒控制參數Γ1的靈敏度分析結果。在給定擾動比例下(如χ1=0.2),配置總成本隨控制參數Γ1的增加而逐步增大。在給定控制參數Γ1(如Γ1=4),云制造成本的擾動幅度越大,配置總成本也越大。因此,決策者應準確地預測云制造成本的擾動幅度、并根據風險預測情況合理地選擇配置結果。

在擾動比例變化情況下考慮云制造時間不確定情況下的產品配置結果,圖4所示為在不同擾動比例下目標函數(配置總成本)隨魯棒控制參數Γ2的靈敏度分析結果。

由圖4可以看出,在擾動比例固定的情況下(如χ2=0.4),配置總成本隨著控制參數Γ2階梯型增長。這是因為在某些情況下,盡管云制造時間出現擾動,但交貨期約束式(5)仍然可以滿足,所以不會導致配置解的改變。因此,在這種情況下,盡管控制參數Γ2增加(例如,當χ2=0.4時,Γ2從2改變到3),但總的配置成本仍然保持不變。此外,隨著擾動比例的增大,總的配置成本也不斷增加,但配置解越來越少。例如,當χ2=1.0時,僅僅在Γ2≤2有最優解,當Γ2取其他值時模型都無解。其原因是,隨著擾動比例的增加,云制造時間的擾動值增大,為應對這種時間上的不確定性,保護函數的值也相應增大,從而導致滿足交貨期約束式(5)的配置解越來越少。由上述分析可以看出,根據擾動比例合理設置魯棒參數的值,從而可以避免出現模型無解的情況。

3.3 同時考慮不確定性和擾動比例

前面分別分析了魯棒控制參數和擾動比例對產品配置結果的影響。下面將同時考慮魯棒參數Γ1、Γ2和擾動比例χ1、χ2變化時對配置決策的影響:擾動比例分別設置為0.1～0.5之間變化。圖5所示為配置總成本隨魯棒參數和擾動比例的變化趨勢。

由圖5可以看出,隨著魯棒控制參數Γ1、Γ2以及擾動比例χ1、χ2的增加,不確定參數個數和參數的擾動值范圍都不斷增加。為抵御這種風險,決策者越來越傾向保守,因而配置總成本更高。此外,由于同時考慮云制造成本和時間的不確定性,魯棒參數和擾動比例的可行取值范圍也相應縮小。例如,當Γ1=Γ2=7時,擾動值＞0.2時,模型已無可行解,故與單獨考慮其中一個因素相比,同時考慮云制造成本和時間不確定性的魯棒控制參數和擾動比例的可行取值范圍會更小。因此,決策者應理性地設置魯棒控制參數和擾動比例。

3.4 約束違例概率

由魯棒優化的定義可知,當魯棒優化問題的不確定參數變化個數不超過魯棒控制參數Γ時,魯棒優化模型能夠確保相應的約束100%滿足,而不違背約束。但是,當不確定參數的變化個數超過Γ時,該約束可能會被違例。該約束違背的概率為[21]

其中,Φ是累積標準正態分布函數。

為進一步分析約束違背概率和配置總成本的關系,隨機生成一個配置問題實例:模塊數為20個,每個模塊的變型實例為3個,模塊的云制造成本、云制造時間、組裝成本和組裝時間均從[20,300]區間內隨機產生。為研究約束式(5)的違背概率,保持魯棒控制系數Γ1=0,而僅僅Γ2發生改變,即云制造成本是一個確定的參數,而云制造時間是一個擾動的參數。表6列出了當Γ2變化時,約束式(5)的違背概率。

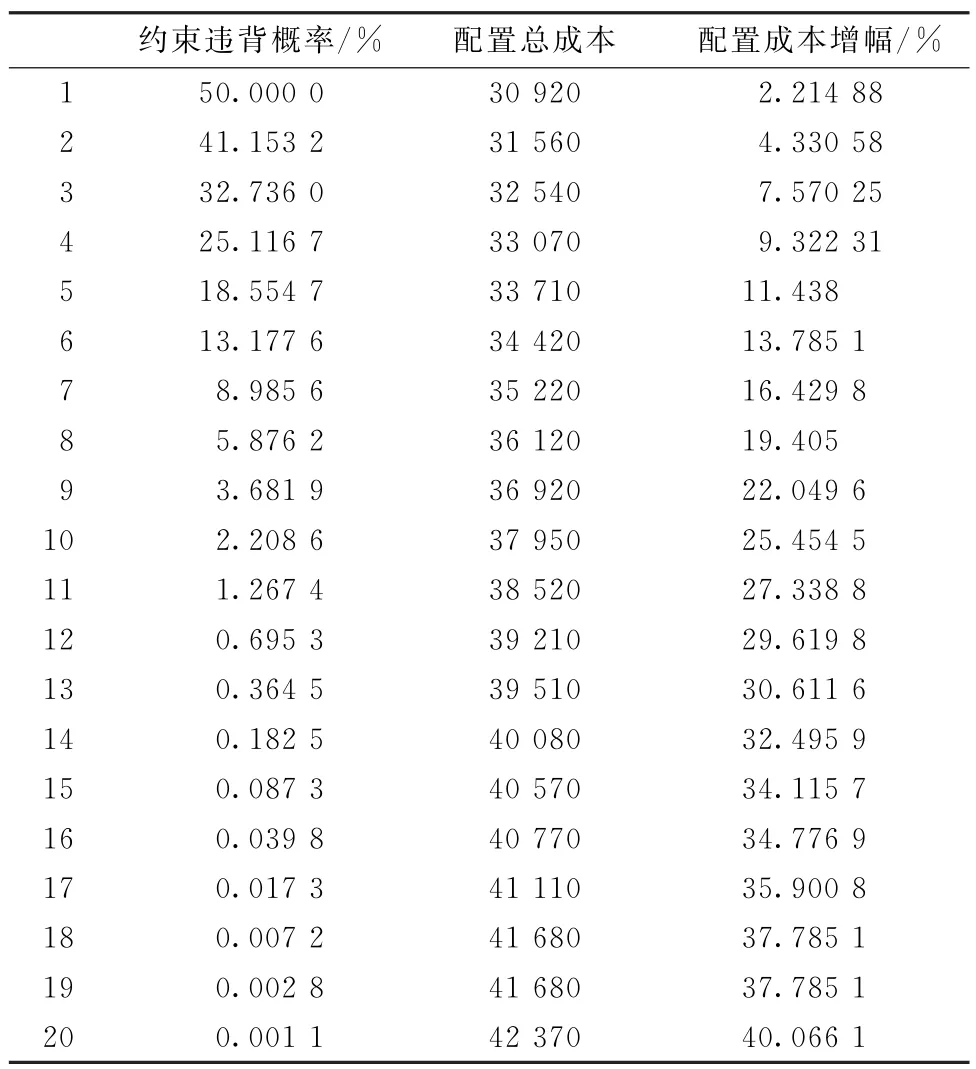
表6 約束違背概率(χ2=0.4)

由表6可以看出,隨著Γ2的增加,決策者越來越偏向保守,約束違背概率越來越低,但配置總成本也顯著增加。由圖6可以看出,配置總成本隨控制參數Γ2邊際遞增。因此,設置合理的Γ2及約束違背概率對決策者至關重要。如果Γ2設置太高,則表示決策者偏向保守,約束違背率將減少,但將會導致配置總成本增加;如果Γ2設置過低,則表示決策過于冒險和樂觀,盡管配置總成本將降低,但約束違背概率增加,將會導致產品的交貨期不能滿足顧客的要求。例如,由表6可見,約束違背概率僅為0.36%。在實際生產中,設置大于13 的Γ2值已無十分必要。誠然,決策者可以根據自己所承受的約束違背概率,合理選擇合適的Γ2值。表7所示為與約束違背概率相對應的Γ2值選擇,其中變動比例θ是指發生擾動的模塊實例數占所有模塊實例數的比值。例如,如果決策者希望約束違背概率小于0.5%,只需設置值為13。即決策者只需從60個模塊實例中選擇出風險最高的13個模塊實例進行風險擾動分析。

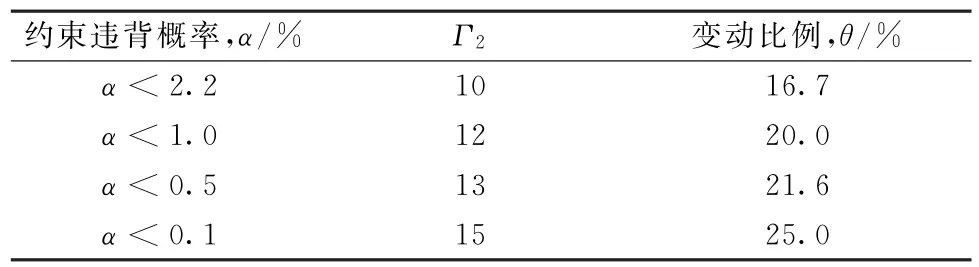
表7 魯棒參數Γ2 的選擇

4 魯棒解的質量驗證

為驗證魯棒模型所求得的配置解的有效性,隨機產生3個具有不同規模的配置問題實例。其中:模塊的云制造名義成本cjk為[50,300]之間的均勻分布,模塊的云制造名義時間Tjk為[40,160]之間的均勻分布;模塊的組裝成本ACjk為[20,60]之間的均勻分布,模塊的組裝時間ATjk為[10,40]之間的均勻分布;訂單數量為1。并假定魯棒控制參數Γ1=Γ2,擾動比例χ1=χ2。對于每個配置問題實例的不同魯棒參數組合(Γ,χ),采用蒙特卡洛的仿真方法產生擾動的云制造時間和云制造成本,使其值落在所定義的擾動區間內。并隨機仿真100次,共仿真27 000次。為了驗證魯棒解的有效性,使仿真產生的擾動模塊個數小于或等于Γ,表8給出了魯棒解和確定模型解的仿真結果比較。表8中問題實例編號|J|×|K|×|I|分別表示模塊數、實例數和訂單數。名義數據下的目標值是分別通過求解確定模型和魯棒模型而得到的。

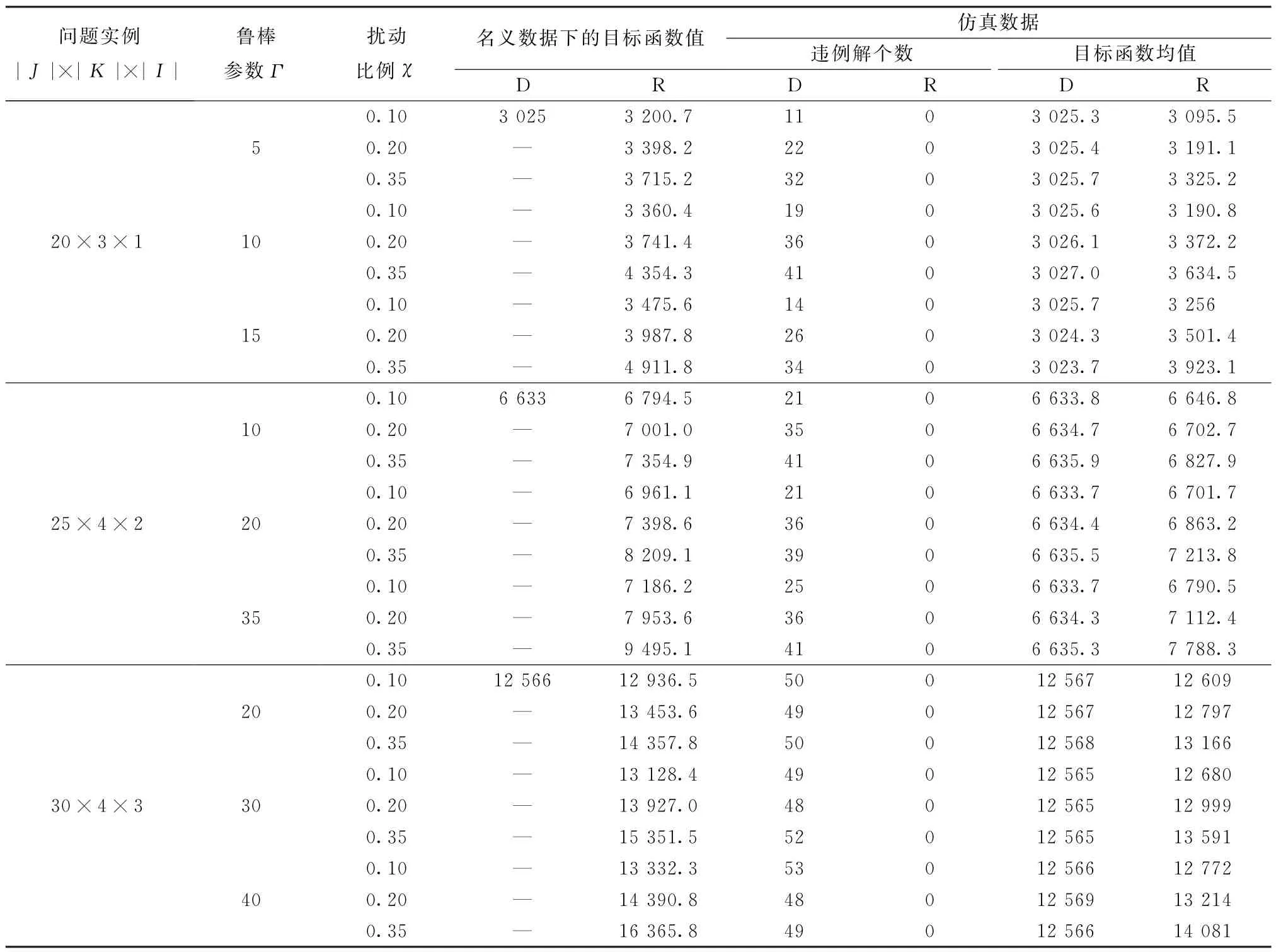
表8 魯棒模型解與確定模型解的比較

由表8可以看出,不論是名義目標值還是仿真目標均值,魯棒模型的目標值均高于確定模型的目標值。這是因為決策者為避免風險而付出的成本代價。但是,在仿真數據的場景下,魯棒模型能夠保證100%的滿足約束,即違例解個數為0,而確定模型違背約束的比例相當高。例如,對于20×3×1 實例,當Γ=10和χ=0.35時,100次仿真中有41次都存在著違背約束的情況。平均來講,確定模型解100次仿真有36次仿真中都存在違例解。可以看出,魯棒模型比確定模型更能抵御不確定因素的沖擊,因而其解也更為穩定,能夠保證在Γ內百分之百的滿足模型的約束。但魯棒模型的配置總成本也高于確定模型的總成本,因而決策者應該平衡目標的最優性和決策的保守性,在滿足產品交貨期和服務質量的前提下,進行理性的最優決策。

5 結語

本文針對云制造模式下的產品配置優化問題,考慮了模塊的云制造成本和時間的不確定性。采用基于budget和區間來刻畫不確定集,以配置總成本之和為目標,建立了云制造模式下的產品配置魯棒優化模型。案例分析表明,隨著魯棒budget控制參數和擾動比例的增加,決策者越來越傾向于謹慎,產品交貨期的約束違背率降低,這表示產品的交貨服務質量提高,但隨之配置總成本會不斷增加。因此,決策者應該對云制造成本和時間做出更為準確的預測,將有助于降低配置總成本。此外,決策者也應避免過度保守,過度增大budget控制參數和擾動比例,也會導致模型無解。進一步采用蒙特卡洛仿真方法,驗證了魯棒模型盡管比確定性模型具有更高的配置成本,但能夠保證產品交貨期約束的滿足,因而魯棒模型也更為穩健。

需要指出的是,云制造過程中模塊的運輸物流、環境因素(如碳排放等)以及云制造中的服務定價問題,本文并沒有涉及,這將是后續研究所應該研究的內容。