具有多模式球面4R機構結構參數研究

劉 偉 劉宏昭 胡旭宇

(1.西安理工大學機械與精密儀器工程學院， 西安 710048; 2.西安工程大學機電工程學院， 西安 710048)

0 引言

多模式并聯機構和多模式混聯機構中含具有多模式的單環結構。一些并聯機構中含有的多模式單環結構使得并聯機構具有多種運動模式。將機構的結構參數看作變量，對單環機構[1]運動模式進行分析時，現有的運動模式分析方法將遇到較大的挑戰[2]。多模式單環機構是多模式多環機構的基礎，對多模式單環機構的運動模式分析時，將機構的結構參數作為變量，研究結構參數對多模式機構運動模式的影響，是多模式機構創新設計需要解決的重要問題之一。

多模式機構運動模式分析方法基本可分為6類：基于旋量理論、基于數值計算方法、基于高階運動學分析、基于幾何圖像方法、基于位移流形理論、基于代數幾何方法。①基于旋量理論方法。在機構多運動模式分析時，需要對機構的每種運動模式的運動旋量進行求解[3]。結合給定結構參數，使用旋量理論對其進行運動模式分析比較簡便有效，使用該理論研究結構參數對機構運動模式影響的文獻較為少見。②基于數值計算方法。過約束機構在折疊結構中應用廣泛[4-5]，設計時往往需要對機構在折疊過程中是否發生運動模式變換進行判斷。數值計算方法在過約束機構運動學方程不具有解析解時，給定結構參數后，對其運動模式的研究可得到理想的結果。當機構結構參數作為變量時，需要進行大量的計算，不易全面分析結構參數對機構運動模式的影響。③基于高階運動學方法。基于高階運動學對機構的多種運動模式進行研究[6-8]，可得一些具有新型運動特征的機構，該方法主要對具有結構參數確定的機構分析其高階運動特征，主要是通過高階運動學分析機構的奇異位形運動特性。④基于幾何圖像方法。根據連桿輸出點的空間位置，通過幾何圖像法對多模式機構模式進行分析[9-10]。通過幾何圖像分析時，需要先確定機構結構參數，目前多使用該方法在分析具有多種移動運動模式機構所具有的運動模式。然而，機構空間運動較移動運動更為復雜，并且機構結構參數變換時，不容易使用該方法全面研究結構參數對機構運動模式的影響。⑤基于位移流形理論方法。位移流形理論在對機構運動模式分析時的能力較為有限[11-12]，主要是通過機構不同位形下，運動副之間的幾何關系，結合機構奇異位形對機構運動模式進行分析。位移流形理論下運動鏈的表達式中不含有機構的結構參數信息，因此目前這方面的相關研究較少。⑥基于代數幾何方法。使用代數幾何方法對機構運動模式進行分析，主要是將機構的運動學方程轉換為代數方程后，對其對應的仿射簇進行相應的準素分解。文獻[13]使用輸入變量與輸出變量的代數方程系數對平面4R機構進行了分類，將其結構參數與八面體空間中的點建立一個映射關系。文獻[14]使用對偶四元數描述機構的約束方程，克服了使用萬能代換求解時，需要對關節轉角為180°時，單獨進行分析的繁瑣計算過程。文獻[15]分析一般面對稱6R機構的運動學方程，得到其具有多種運動模式時，機構參數所滿足的條件，對這類6R機構的運動特性進行了全面分析。該方法研究了機構結構參數對一類6R機構運動模式的影響，文中指出存在一部分具有多種運動模式的該類6R機構，并不符合其提出的多運動模式判斷依據。文獻[16]使用代數計算軟件，針對具有不同結構參數的3RER具有的運動模式進行全面分析。代數幾何方法在機構運動模式分析時，一般能取得比較理想的結果。然而，由于機構運動學方程和機構結構參數數目的增多，使得機構運動模式分析困難。一方面，變量數目一定程度上決定了運動模式分析的復雜程度；另一方面，復雜的運動模式分析對軟件計算[17]的依賴程度較高，文獻[18]研究表明，通過軟件計算分析機構運動模式時，需要對計算結果進行特殊的分析處理才能得到正確結果，而這個過程較繁瑣。

綜上所述，基于旋量理論、數值計算、高階運動學分析、位移流形理論，尚不能全面分析機構結構參數對其運動模式的影響。雖然現有文獻中基于代數幾何方法可以全面分析機構結構參數對機構運動模式的影響，但是該方法尚不能對機構實際具有的運動模式結果進行全面解釋。使用軟件分析結構參數對機構運動模式的影響計算量太大，且有時需要對計算結果進行分析才能得到正確結果。

本文使用代數幾何理論，基于多項式可因式分解的條件，結合機構的運動模式，提出一種分析結構參數對球面4R機構運動模式影響的方法。

1 確定具有多種運動模式球面4R機構結構參數的方法

一般情況下，將機構運動學方程轉換為代數方程后，當機構構型一定時，機構運動學方程的形式和結構基本確定，即運動學代數方程關于關節變量的各個多項式組成即可確定。不同的機構結構參數代入機構運動學方程，從而使得關節變量多項式系數發生改變。如果機構運動學代數方程可以在實數范圍內進行準素分解[19]，則該機構具有多種運動模式。那么可以根據機構運動學代數方程分析得到可準素分解的條件，求解代數方程中與機構結構參數有關的系數，從而設計具有多種運動模式的機構。文獻[20]指出，對于一個代數方程而言，對該代數方程對應的多項式進行因式分解，即是一種特殊的準素分解。文獻[19]給出了判斷代數方程是否可以進行因式分解的依據，即該代數方程可寫成有理分式的參數方程時，該代數方程可因式分解。

綜上所述，可對球面4R機構對應的代數方程判斷其是否可轉換為有理分式表達的參數方程，對其運動模式進行分析。

使用因式分解方法對多運動模式球面4R機構結構參數對其運動模式影響的分析步驟為：

(1)根據球面4R機構的4個連桿的機構結構參數建立運動學方程

f(θi,θj)=0

(1)

(2)使用萬能代換替換球面4R機構轉動副關節變量θi、θj的三角函數，化簡得到關于關節變量θi、θj的代數方程為

ft(ti,tj)=0

其中

ti=tan(θi/2)tj=tan(θj/2)

(3)將球面4R機構代數運動學方程中各多項式系數，分別置零后組合，得到結構參數滿足的公式。

(4)將步驟(3)得到結構參數滿足的關系，代入步驟(1)中球面4R機構的運動學方程，分析任意關節變量θi=π時的任意組合下機構具有的運動模式。

(5)將步驟(3)得到的不同結構參數滿足的公式，代入步驟(2)中球面4R機構的運動學代數方程，判斷該方程是否可進行因式分解，從而分析機構具有的運動模式。

(6)結合步驟(4)、(5)的結果，得到球面4R機構具有不同運動模式時，結構參數滿足的關系。

2 球面4R機構運動學方程與多模式結構參數的關系

2.1 球面4R機構運動學方程

如圖1所示球面4R機構，4個轉動副R1、R2、R3、R4軸線相交于點o，αij為轉動副Ri轉動軸線zi繞軸線y′i轉動到與軸線zi+1重合時的角度。θi為軸線xi繞軸線zi轉動到與軸線x′i重合時的角度。可選取轉動副R1、R4的關節變量轉角θ1、θ4建立運動學方程。文獻[21]給出的球面4R機構的運動學計算公式為

圖1 球面4R機構結構參數Fig.1 Structural parameters of spherical 4R mechanism

-s12s41c34c1-s12c41s34c1c4+s12s34s1s4-c12s41s34c4+
c12c41c34-c23=0

(2)

式(2)中sij、cij表示αij的正弦和余弦，si、ci表示轉角θi的正弦和余弦。式(2)為第1節中步驟(1)中f(θi,θj)=0，i=1，j=4。即式(2)是關于關節變量θ1、θ4的運動學方程。

2.2 球面4R機構運動學方程轉變為代數方程

使用萬能代換，t1=tan(θ1/2),t4=tan(θ4/2)，將球面4R運動學方程式(2)整理得到

(3)

其中

A=s12s41c34-s12c41s34+c12s41s34+c12c41c34-c23=
c34cos(α12-α41)-s34cos(α12-α41)-c23=
cos(α12-α41+α34)-c23
B=-s12s41c34+s12c41s34+c12s41s34+c12c41c34-c23=
s12sin(α34-α41)+c12cos(α34-α41)-c23=
cos(α12+α41-α34)-c23
C=s12s41c34+s12c41s34-c12s41s34+c12c41c34-c23=
s12sin(α34+α41)+c12cos(α34+α41)-c23=
cos(α12-α41-α34)-c23
D=4s12s34
E=-s12s41c34-s12c41s34-c12s41s34+c12c41c34-c23=
-s12sin(α34+α41)+c12cos(α34+α41)-c23=
cos(α12+α41+α34)-c23

式(3)為第1節步驟(2)中的ft(ti,tj)=0。

2.3 代數方程多項式系數分別置零進行組合

不考慮轉動副R1和R2以及R3和R4軸線重合，機構中存在局部轉動自由度的情況，因而式(3)中D≠0。

當a12-a41+a34+a23=2kπ(k=0,±1,±2,…,±n)時，式(3)中A為零，該機構自由度為零，這種情況舍去不做分析。同理，可根據式(3)，當A=0,B=0,C=0,E=0時分別可得到

(4)

球面4R機構處于約束奇異位形時，4個轉動副軸線共面。關節轉角θ1、θ4只存在4種情況(θ1=0°，θ4=0°；θ1=0°，θ4=180°；θ1=180°，θ4=0°；θ1=180°，θ4=180°)時，球面4R機構處于約束奇異位形，此時機構的運動模式將具有改變的可能性。將上述4組數值，代入式(2)，變換為式(3)的代數方程，分別得到E=0，B=0，C=0，A=0。即當該方程系數A、B、C、E分別為零時，球面4R機構具有4個轉動軸線在同一平面的機構奇異位形。

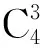
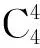
由于轉動副R1、R4均連接機架，可將分別滿足條件B=0和條件C=0的機構看作一種機構。同理，⑤和⑥、⑨和、和同為一類機構。因而總共可分為11種情況。

3 不同結構參數球面4R機構運動模式分析

根據文獻[19]可知，當一個代數方程轉變為參數方程后，參數方程均為有理代數分式時，則該代數方程不能被因式分解。從而可對球面4R機構運動學代數方程是否可以進行因式分解進行判斷，進而得到球面4R機構的運動模式。

3.1 球面4R機構運動模式(1號A=0)

當a12-a41+a34-a23=2kπ(k=0，±1,±2,…，±n)，且θ1=±π或θ4=±π時，根據式(2)得到，θ4或θ1為定值，此時機構不具有固定軸線轉動運動模式。

當a12-a41+a34-a23=2kπ(k=0，±1,±2,…，±n)，且θ1≠±π且θ4≠±π時，此時式(3)中的系數A為零，且B、C、D、E均不為零時，將方程式(3)看作t4的一元二次方程，得到

(5)

其中

D2-4BC=16s12s34s41s23

式(5)可以分解時，需要t4的表達式可以寫成有理分式的形式，需滿足D2-4BC>0、BE=0，或D2-4BC=0、BE<0，可得

此時機構的運動學方程可因式分解。

然而，當球面4R機構結構參數僅使得式(3)中A為零，則BE、D2-4BC不為零。因而，此時式(3)不能寫成兩個有理分式相乘的形式，可知此時式(3)不能分解因式，當球面4R機構結構參數僅滿足A為零，當θ1≠±π且θ4≠±π時，機構只具有一種變軸線轉動運動模式。

現以結構參數使得式(3)中A為零的球面4R機構為例，對其運動模式進行分析。機構的結構參數α41=90°、α12=60°、α23=30°、α34=60°，該結構參數滿足a12-a41+a34-a23=2kπ，且該機構結構參數不滿足式(4)中的其他幾個關系式，如圖2球面4R機構3維模型所示。由圖2d可知，當機構處于約束奇異位形時，其存在運動分岔的可能性，但當使得θ4隨θ1變化的斜率不發生突變時，機構將通過該約束奇異位形且保持運動不發生分岔。

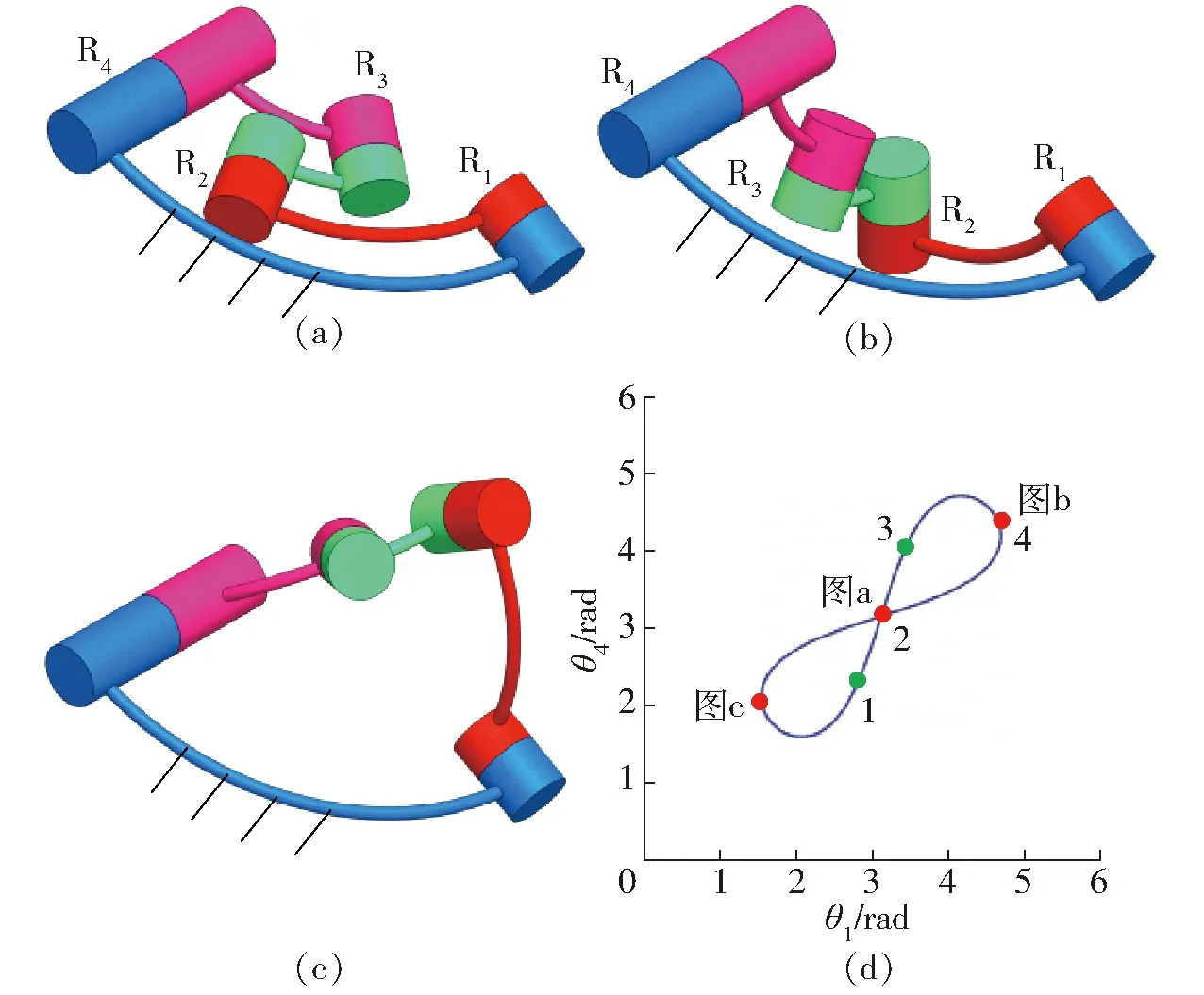
圖2 球面1號4R機構位形Fig.2 Configuration of No.1 spherical 4R mechanism

當機構從圖2d中點1機構位形，保持θ4隨θ1變化的速率與點1、2、3所在曲線斜率相同時，該機構能動態通過點2對應的機構約束奇異位形，到達點3所對應的機構位形，即該機構可以通過點2處約束奇異位形而不發生運動分岔。實際上當機構速度不為零，從圖2d點1對應位形運動到點2對應位形時，θ4隨θ1變化的速率與點1、2所在曲線斜率相同。則當機構從點1所在機構位形運動到點2對應位形時，速度不為零時，即可通過點2所示約束奇異位形，且不發生運動分岔現象。同理，當機構從點3所示位形，運動到點4所示機構死點位形時，使得θ1的速度不為零時，機構可通過該死點位置。可以發現，在機構的點2對應的約束奇異位形和點4對應的死點位形下，機構均可動態通過，最終可到達所有的機構位形。

同理可知當式(3)中的系數B=0，或C=0，或E=0時，球面4R機構只具有1種變軸線轉動運動模式，且結構參數滿足這些條件的球面機構均與圖2所示機構類似，機構可動態通過約束奇異位形，可運動到機構所有的位形。

3.2 球面4R機構運動模式(5號A=B=0)

當a12-a41+a34-a23=2kπ,a12+a41-a34-a23=2kπ，θ1=±π時，將機構結構參數代入式(2)，θ4為定值，此時機構不具有定軸轉動模式。θ4=±π時，將機構的結構參數代入式(2)，整理得到恒等方程0=0。可知θ1可任意取值，機構具有一種以轉動副R1為軸線的定軸轉動運動模式。

當θ1≠±π,θ4≠±π時，A、B為零，C、D、E均不為零，整理式(3)得到的方程為二元二次方程。將該方程看作t1的一元二次方程，得到

(6)

其中

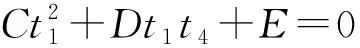
然而，當球面4R機構結構參數僅滿足A、B為零時，CE、D均不為零，因而式(6)不能分解因式。從而，根據運動模式的定義可知，當球面4R機構結構參數僅滿足A、B為零，當θ1≠±π,θ2≠±π時，連桿的瞬時軸線在隨t1、t4不斷變化，因而此時機構只具有一種變軸線運動模式。

現以結構參數使得式(3)中A、B為零的球面4R機構為例，對其運動模式進行分析。如圖3球面4R機構的3維模型所示，機構的結構參數α41=90°，α12=45°，α23=45°，α34=90°，該結構參數滿足式(4)中的關系式a12-a41+a34-a23=2kπ,a12+a41-a34-a23=2kπ。從圖3d可知，當機構處于約束奇異位形時，其存在運動分岔的可能性，但當使得θ4隨θ1變化的斜率不發生突變時，機構將通過該約束奇異位形且保持運動模式不發生改變。

當機構從圖3d中點1機構位形(圖3b)，保持θ4隨θ1變化的變化率與點1、2所在曲線斜率相同時，該機構能動態通過點2對應的機構約束奇異位形(圖3a)，但無法到達點3所對應的機構位形(圖3c)，即該機構可以通過點2處約束奇異位形而不產生運動分岔。同理，當機構從圖3d中點3機構位形，保持θ4隨θ1變化的變化率與點2、3所在曲線斜率相同時，該機構能動態通過點2對應的機構約束奇異位形，但無法到達點1所對應的機構位形，即該機構可以動態通過點2處約束奇異位形而不發生運動模式改變。

圖3 球面5號4R機構位形Fig.3 Configuration of No.5 spherical 4R mechanism

從圖3d可知，點1所對應的機構位形變換到點3所示機構位形時，通過在圖3d點2所示位形時，θ4隨θ1變化的變化率需要發生突變，從而實現機構運動模式的改變。一般情況下，使機構在運動中實現圖3d所示兩種運動模式的變換，十分的困難。可以使機構處于點2所示奇異位形時，保持機構靜止不動，使得轉動副R4和R1的轉角速度為零，然后控制轉動副R4與轉動副R1轉動實現機構運動模式的變換。

同理可知，當式(3)中的系數A=B=0，或A=C=0，或B=E=0，或C=E=0時，球面4R機構只具有1種定軸轉動和1種變軸線轉動共2種運動模式。

3.3 球面4R機構運動模式(8號B=C=0)

當a12+a41-a34-a23=2kπ,a12-a41-a34+a23=2kπ且θ1=±π或θ4=±π時，根據式(2)得到，θ4或θ1為定值，此時機構不具有固定軸線轉動運動模式。

當θ1≠±π,θ4≠±π時，將8號球面機構結構參數代入式(3)整理得到B、C為零，A、D、E均不為零，得到的方程為二元四次方程，即

A(t1t4)2+Dt1t4+E=0

(7)

其中

如圖4球面4R機構的3維模型所示，機構結構參數α41=90°、α12=45°、α23=90°、α34=45°。該結構參數滿足式(4)中的關系式a12+a41-a34-a23=2kπ,a12-a41-a34+a23=2kπ，如圖4e所示，當機構處于約束奇異位形時，其存在運動分岔的可能性，但當使得θ4隨θ1變化的斜率不發生突變時，機構將通過該約束奇異位形且保持運動不發生分岔。點3與點6所對應的機構位形相同，點1與點5所對應的機構位形相同。從圖4e所示點1位形通過點2到達點3，通過點6到達點5機構位形，這整個運動過程屬于第1種運動模式；從圖4e所示點1位形通過點7到達點6，通過點3、4到達點5機構位形，這整個運動過程屬于第2種運動模式。上述兩種運動模式下，連桿的瞬時轉動軸線均隨轉角θ1和θ4不斷發生變化，即8號球面機構只具有兩種變軸線轉動運動模式。使機構處于奇異位形時，保持機構靜止不動，使得轉動副R4和R1的轉角速度為零，然后控制轉動副R4與轉動副R1轉動實現機構運動模式的變換。

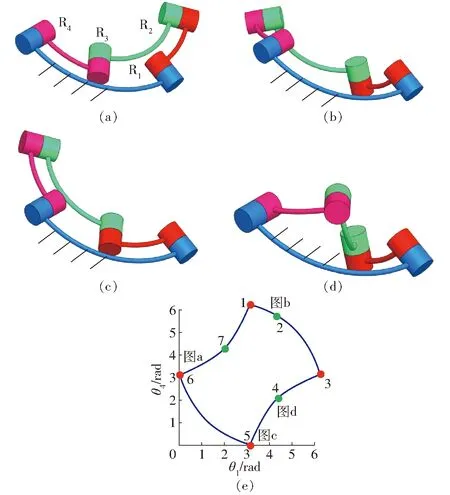
圖4 球面8號4R機構位形Fig.4 Configuration of No.8 spherical 4R mechanism

同理可知，當式(3)中的系數B=C=0時，球面4R機構只具有2種變軸線轉動運動模式。

3.4 球面4R機構運動模式(14號B=C=E=0)

當a12+a41-a34-a23=2kπ,a12-a41-a34+a23=2kπ,a12+a41+a34+a23=2kπ，且θ1=±π或θ4=±π時，根據式(2)得到，θ4或θ1為定值，此時機構不具有固定軸線轉動運動模式。

當θ1≠±π,θ4≠±π時，將14號球面機構結構參數代入式(3)整理得到B、C、E為零，A、D均不為零，得到的方程為二元四次方程

t1t4(At1t4+D)=0

(8)

當球面4R機構結構參數僅滿足B、C、E為零，A、D均不為零，該式可以分解因式。從而，根據運動模式的定義可知，當球面4R機構結構參數僅滿足B、C、E為零，球面4R機構恒具有3種運動模式。兩種為定軸轉動模式，一種為變轉動軸線轉動模式。

如圖5所示，球面4R機構的3維模型機構的結構參數α41=120°、α12=60°、α23=120°、α34=60°。該結構參數滿足式(4)中的關系式，a12-a41+a34-a23=2kπ，a12-a41-a34+a23=2kπ,a12+a41+a34+a23=2kπ。

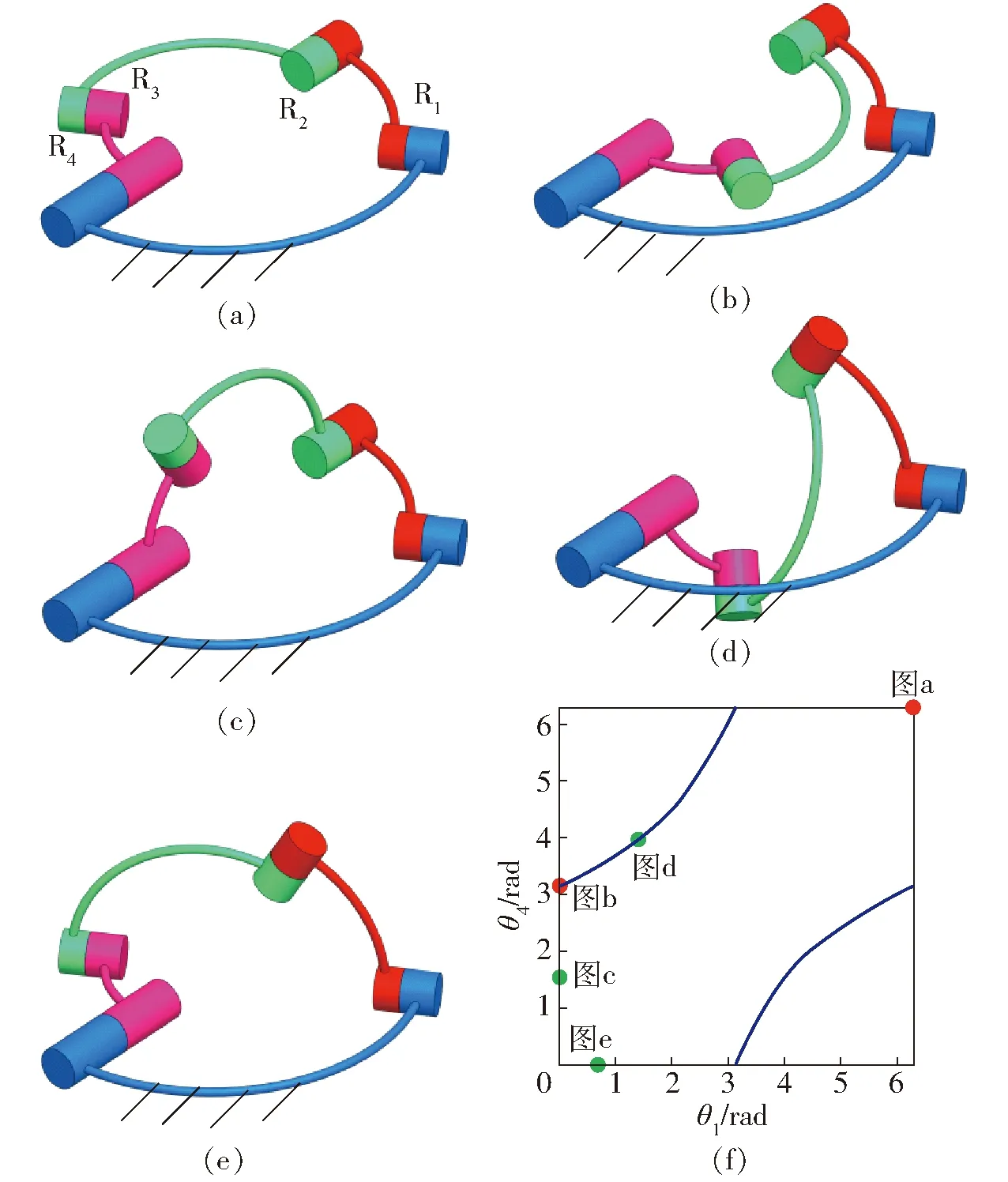
圖5 球面14號4R機構位形Fig.5 Configuration of No.14 spherical 4R mechanism

如圖5f所示，當機構處于約束奇異位形時，其存在運動分岔的可能性，但當使得θ4隨θ1變化的斜率不發生突變時，機構將通過該約束奇異位形且保持運動模式不發生改變。使機構處于奇異位形時，保持機構靜止不動，使得轉動副R4和R1的轉角速度為零，然后控制轉動副R4與轉動副R1轉動實現機構運動模式的變換。

同理可知，當式(3)中的系數A=B=C=0,或A=B=E=0,或A=C=E時，球面4R機構只具有2種定軸線轉動和1種變軸線轉動共3種運動模式。

3.5 球面4R機構運動模式(15號A=B=C=E=0)

將15號球面4R機構結構參數代入式(2)，當θ1=±π時，得到0=0，即該式恒成立。即轉動副R1的轉角θ1為±π時，轉動副R4的轉角θ4可自由轉動，此時對應球面4R機構連桿可以繞轉動副R4的軸線做定軸轉動。當θ4=±π時，將該式整理得到0=0，即該式恒成立。即轉動副R4的轉角θ4為±π時，轉動副R1的轉角θ1可自由轉動，此時對應球面4R機構連桿可以繞轉動副R1的軸線做定軸轉動。

當θ1≠±π,θ4≠±π時，將15號球面機構結構參數代入式(3)整理得到A、B、C、E為零，D不為零，得到二元二次方程

t1t4=0

(9)

當球面4R機構結構參數僅滿足A、B、C、E為零，D不為零，該式可以分解因式。即t1=0對應轉動副R1的轉角θ1為0時，轉動副R4的轉角θ4可自由轉動，此時對應球面4R機構連桿可以繞轉動副R4的軸線做定軸轉動。t4=0對應轉動副R4的轉角θ4為0時，轉動副R1的轉角θ1可自由轉動，此時對應球面4R機構連桿可以繞轉動副R1的軸線做定軸轉動。

從而可知，當球面4R機構結構參數僅滿足A、B、C、E為零，球面4R機構恒具有4種定軸轉動運動模式。

如圖6球面4R機構的3維模型所示，機構的結構參數α41=90°、α12=90°、α23=90°、α34=90°，其結構參數滿足式(4)。從圖6g可知，當機構處于約束奇異位形時，其存在運動分岔的可能性，但當使得θ4隨θ1變化的斜率不發生突變時，機構將通過該約束奇異位形且保持運動模式不發生改變。使機構處于奇異位形時，保持機構靜止不動，使得轉動副R4和R1的角速度為零，然后控制轉動副R4與轉動副R1轉動實現機構運動模式的變換。

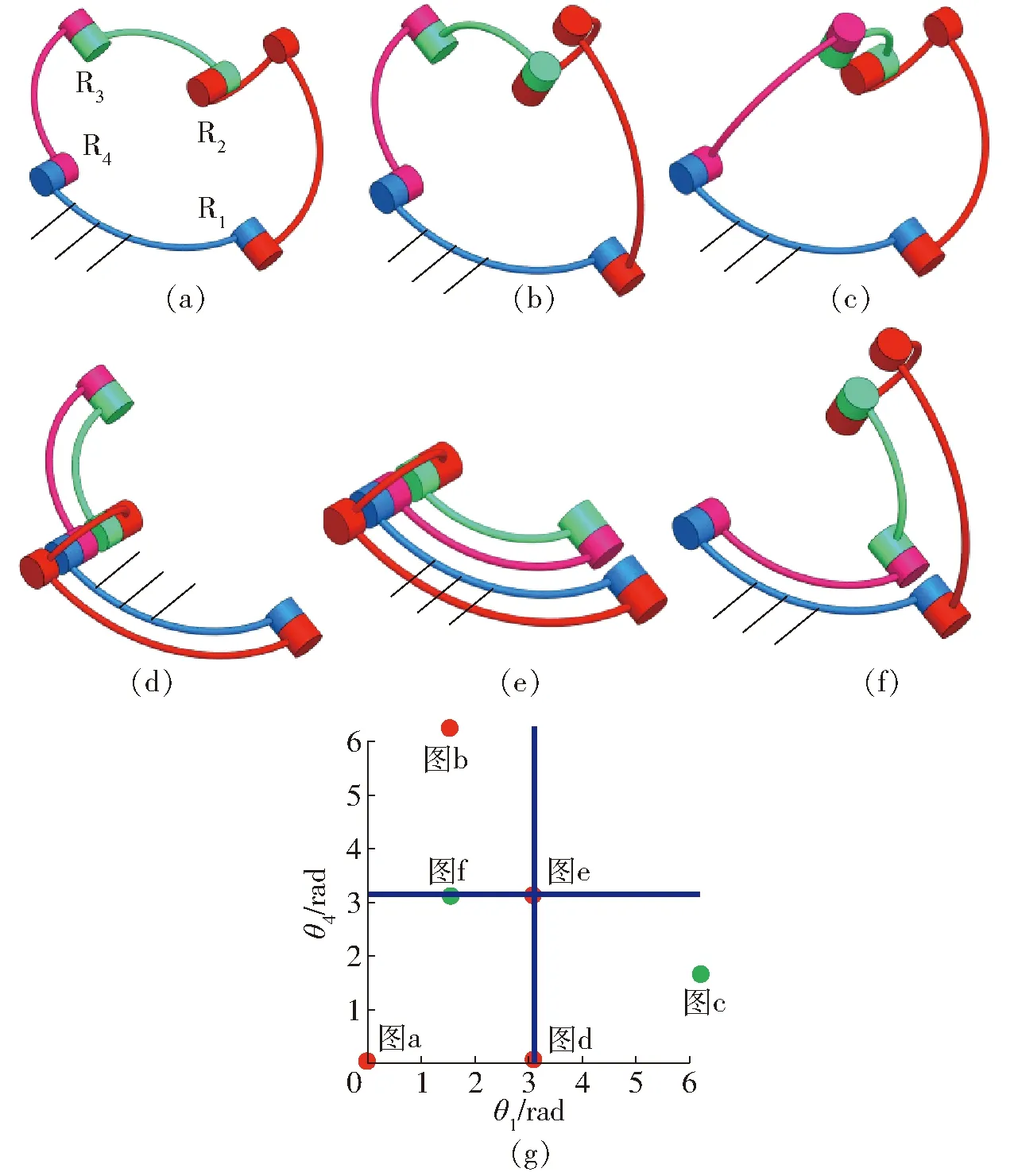
圖6 球面15號4R機構位形Fig.6 Configuration of No.15 spherical 4R mechanism

綜上所述，可將式(3)的多項式系數A、B、C、E分別置零，進行組合后，得到的結構參數關系式，可設計具有不同運動模式特征的球面4R機構。這類球面4R機構所具有的運動模式如表1所示。表1中Sm為機構運動模式數目，Sf為球面4R機構固定軸線轉動運動模式數目，Sv為球面4R機構變軸線運動模式數目。

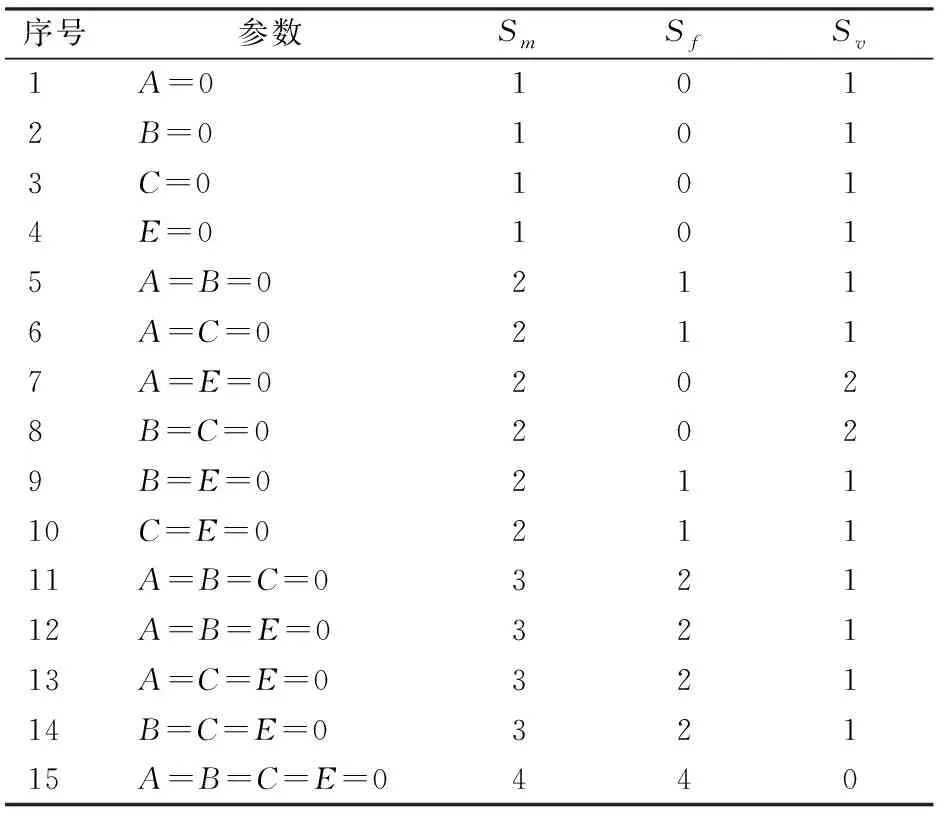
表1 具有約束奇異位形的球面4R機構運動模式數目Tab.1 Motion mode of spherical 4R mechanism with constrained singular configuration

根據表1可知，1～4號機構只具有1種變軸線轉動運動模式；5、6、9、10號機構只具有1種定軸線和1種變軸線共2種轉動運動模式；7、8號機構具有2種變軸線共2種轉動運動模式，11～14號機構具有1種變軸線、2種定軸線3種轉動運動模式；15號機構具有4種定軸線轉動運動模式。

4 球面4R機構約束奇異位形瞬時轉動軸線

建立如圖7所示的球面4R機構坐標系，當機構的4個轉動副軸線在XOY平面內，相交于點O。轉動副R4的軸線與向量OA重合，轉動副R1的軸線與向量OB重合。轉動副R1、R2軸線所在平面Σ12與轉動副R4、R3軸線所在平面Σ43的交線與OC重合，轉動副R4繞向量OA轉動有限角度θ4后，轉動副R1轉動有限角度θ1，轉動副R4、R3軸線所在平面OAC的法線沿Z軸方向，繞轉軸R4轉動π-θ4；轉動副R1、R2軸線所在平面OBC的法線沿Z軸方向，繞轉軸R1轉動θ1。

圖7 球面4R機構連桿瞬時軸線幾何關系Fig.7 Geometric relationship of instantaneous axis of connecting rod of spherical 4R mechanism

平面OAC的法線在OXYZ坐標系中為

(10)

平面OBC的法線在OXYZ坐標系中為

(11)

平面OAC、OBC法線的共垂線平行于向量

(12)

式(12)可寫成形式

(13)

式(12)為球面4R機構連桿的瞬時轉動軸線的方向向量。當球面4R機構趨近于奇異位形時，式(12)的極限值即為球面4R機構趨近于奇異位形時連桿的瞬時轉動軸線。當球面4R機構趨近于奇異位形時c1/c4=±1。因而，約束奇異位形下連桿瞬時轉動軸線方向向量式(13)的極限值為

(14)

式(14)可通過幾何方法進行驗證。如圖7所示OA與轉動副R4的軸線重合，OB與轉動副R1的軸線重合。CA為轉動副R4、R3所在平面Σ43的直線，CB為轉動副R1、R2所在平面Σ12的直線。OC即為上述兩平面的交線，即球面4R機構連桿的瞬時轉動軸線。點A、B均在平面OXY上，點C在平面OXY上的投影為點D，DA垂直于OA，BD垂直于OB。由于CD垂直于AD、CD垂直于OA，且AD垂直于OA，因而根據轉動副R4的轉角θ4得出∠CAD為π-θ4。同理，根據轉動副R1的轉角θ1得出∠CBD為π-θ1。

根據圖7的幾何關系，可得到

(15)

(16)

(17)

根據式(15)～(17)可得到

(18)

球面4R機構在運動分岔時分3種情況，第1種，兩分岔軌跡均為變軸線運動模式。第2種，兩分岔軌跡均為定軸線運動模式。第3種，兩分岔軌跡中一個為定軸線運動模式，另外一個為變軸線運動模式；計算分岔運動軌跡在機構位形趨近于約束奇異位形時s4/s1的值。結合上述3種情況由式(14)可知，表1中球面4R機構在趨近于約束奇異位形時，不同分岔運動軌跡連桿的瞬時轉動軸線均不重合。

5 結論

(1)提出一種研究球面4R機構運動學代數方程可分解因式的條件的方法，全面分析了結構參數對其運動模式的影響。

(2)發現了5類具有約束奇異位形的球面4R機構，其中多模式球面4R機構可分為4類。即具有1種定軸線和1種變軸線共2種轉動運動模式，具有2種變軸線共2種轉動運動模式，具有1種變軸線、2種定軸線3種轉動運動模式和具有4種定軸線轉動運動模式，總共4類多模式球面4R機構。

(3)具有約束奇異位形的球面4R機構處于約束奇異位形時，雖然其運動可能產生分岔，但其運動模式不一定發生改變。因而，運動分岔機構與多模式機構不能等同。球面4R機構處于約束奇異位形時，其連桿的瞬時轉動軸線均不重合。