相似歷史數據段高效查找方法研究*

龐向坤 高 嵩 張緒輝 顏 慶

（國網山東省電力公司電力科學研究院 濟南 250002）

1 引言

隨著新能源發電規模不斷擴大，其間歇性、波動性等為電網穩定運行帶來了日益嚴峻的挑戰。由于火電機組實發功率具有高度的可調節性，其對電網多類型機組協調及穩定運行發揮日益突出的支撐作用。因此，提高火電機組的平穩運行水平，在一定意義上說就是保障新能源消納，促進了電網多類型機組協調和穩定運行。

火電機組運行過程中，經常出現運行異常導致機組降負荷情況發生，降低了火電機組負荷調節能力。關于火電機組運行異常監控已經有眾多的研究結果［1~5］，但在發現生產異常后，及時找出發現異常根源，提高異常處理效率，則是保障機組恢復生產能力的重要環節，目前相關研究結果較少。

當前，火力發電生產過程的信息化和智能化建設不斷深入，海量生產過程數據被采集并存儲。鑒于歷史數據中包含有豐富的可用信息，因此，歷史數據挖掘得到的信息，既可以用于火力發電過程管理與優化，也可以應用于火力發電過程監控等，對于提高火力發電生產效益和安全性等具有重要的意義，如文獻［6~9］均從數據挖掘方法出發，來分析生產過程異常或故障原因。但是由于歷史數據的維度急劇升高且受噪聲影響，查找歷史數據相似數據段主要面臨查詢效率不高和準確性較低的問題。

為了提高歷史數據查詢效率和準確性，近年來研發的技術方法主要是通過簡化數據結構保留主要特征，實現降低原始數據維度的目的。文獻［10］提出一種基于分段聚合近似（PAA）的時間序列早期分類方法，運用PAA 對時間序列樣本進行維數約簡。文獻［11］提出了符號聚合近似轉換（SAX）技術，主要是基于分段聚合近似（PAA）技術進行數據化簡并離散化，將各個數據段用其均值表示，然后采用預設斷點將PAA 系數轉換為SAX 符號。文獻［12］定義了極值噪聲和轉折點，在此基礎上提出了基于轉折點的分段線性表示方法。文獻［13］提出了剪輯技術或定極限技術，實現對數據的壓縮。文獻［14］提出基于形態特征的時間序列符號聚合近似方法，綜合考慮分段序列的均值和數據分布的形態特征，并且通過論域轉化對它們實現符號轉化。文獻［15］針對PAA 算法對每一區間都平均對待所存在的不足，提出一種基于小波熵的時間序列分段聚合近似表示（PAA_WE）方法。

雖然上述方法均存在其應用場景，但是也存在一定的不足。例如，PAA技術雖然可以降低數據維度，但沒有考慮數據段的趨勢信息。在充分借鑒國內外現有相似數據段查找方法的基礎上，本文采用了一種新型的數據表示方法，該方法將原歷史數據轉換為二進制表示形式，采用分段聚合近似（PAA）方法和擴展的剪輯技術合并了原歷史數據的趨勢和數值信息，實現了數據降維，提高了相似特征數據段查找效率和精度。

2 所提方法

本文以實現異常根源診斷為目的，充分利用所選取的目標數據集中各段數據的異常根源信息，當生產運行過程中異常狀況出現時，通過查找當前異常數據段在目標數據集中的相似數據段，以其中的異常數據段為參考，確定當前運行異常的出現的根源。

2.1 時間序列的符號表示

本文采用了一種數據的二進制表示方法［16］，該方法是將給定的數據序列數據轉換成長度為2ω的布爾符號表示序列，此處ω表示數據序列PAA的分段數。在布爾符號表示過程中，每一個PAA子段采用兩位布爾數表示，其第一位布爾數值表示數據幅值信息，通過比較數據段前幅值與其均值得到；第二位布爾數值表示趨勢信息，通過比較數據段前數值與最近點的位置得到。對歷史運行數據X，以單步滑動窗口法得到X的子序列X[i]，然后采用PAA 方法對X[i]進行分段，對每個子數據段按如下方式進行其趨勢和數值信息的符號轉換［16］：

式（1）、（2）中，xˉk為時間序列X分段后第k子數據段的樣本均值，Xˉi為X[i]的均值；式（3）中，xˉk+1為時間序列X分段后第k+1 個子數據段的樣本均值，即xˉk+1=(xk+1+xk+2)/2。

數據二進制符號表示后，對以相應結果進行融合，數據幅值信息均以二進制序列奇數位表示，趨勢信息均以二進制序列偶數位表示，X[i]對應的二進制序列以B[i]表示，B[i]={b(i·ω+1)，b(i·ω+2)，…，b(i·ω+ω)}，具體轉換過程如圖1示例。

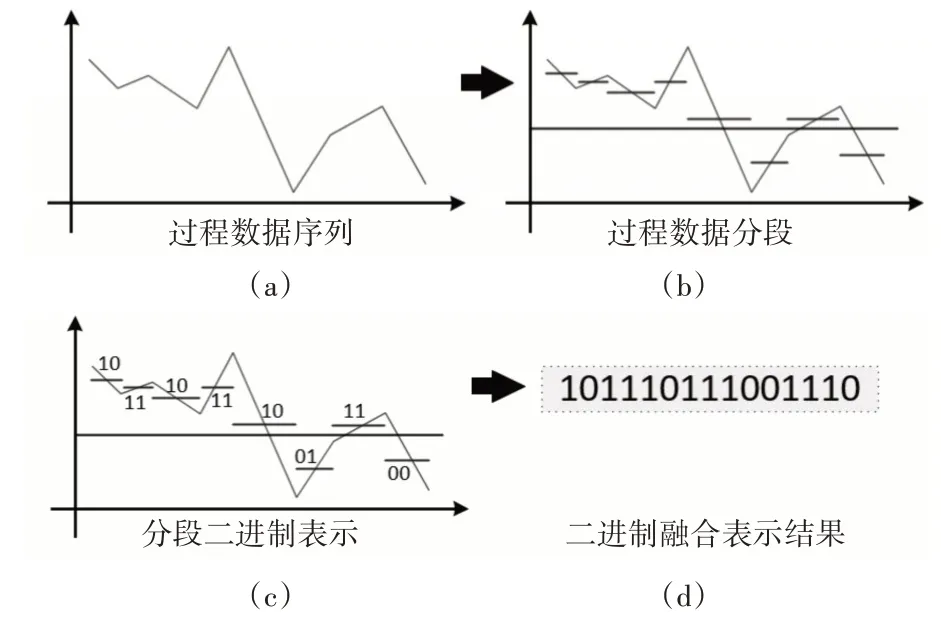
圖1 數據序列轉換為二進制序列過程示意圖

2.2 形成目標數據集

完成二進制數據轉換后，得到BC和B[i] ，i∈[1，N-1]，為了篩選出相關性較高的子數據段，可以指定相似性閾值ε，將BC和B[i]相似性大于閾值ε的子序列對應的X[i]提取出來，形成目標數據集。

二進制數據序列BC和B[i]的相似性采用符號相似系數度量，在此，BC={bc(1)，bc(2)，…，bc(ω)}，B[i]={b(i·ω+1)，b(i·ω+2)，…，b(i·ω+ω)}，其符號相關系數計算公式如下：

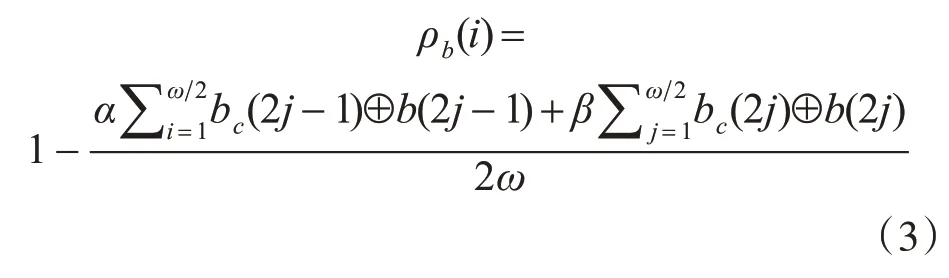
式（3）中，α和β分別是對數值信息和趨勢信息所加的權重，滿足0 ＜α，β＜1。α和β的取值可根據需要查找的異常數據段的特征進行選擇。式（3）中，分子分別為二進制序列的奇數位和偶數位的漢明距離［17］。式（3）中，符號⊕表示布爾異或運算，且ρb的取值范圍為[0，1]。

最后，將ρb(i)大于閾值ε的X[i]提取出來，設共有L組滿足條件，則組成的時間序列候選集，候選集Cs中的數據維數將遠小于，因此將大幅度縮小相似數據段查找范圍，使得查找速度大幅提高。為了避免單步滑窗提取X[i]所帶來的ρb(i)在X局部取過多較大值，造成候選數據集維數過高的問題，選取ρb(i)大于閾值ε時，應滿足任意兩個選定的相關系數ρb(i)和ρb(j)之間滿足 ||i-j＞ω2。

2.3 確定相似異常數據段

采用二進制序列表示原數據，必然造成式（3）中的相似性計算結果較為寬泛，因此需要對候選集中數據進一步與當前異常數據進行相似性分析。

對Xl[i]={x(i·ω+1)，x(i·ω+2)，…，x(i·ω+ω)}，其與的皮爾遜相關系數計算公式如下：

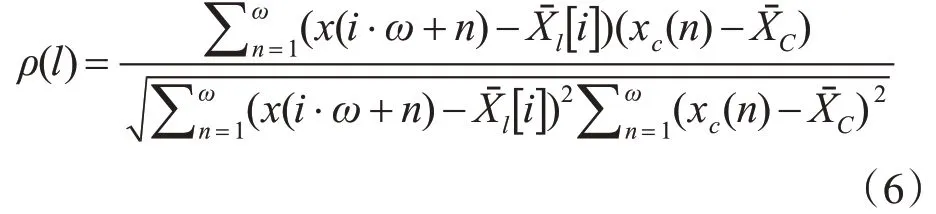
對于式（6）中得到的計算結果，按從大到小的順序進行排序，相關系數越大則時間序列的相似程度越高，實現查找相似時間序列的目標。

3 仿真案例

為了驗證所述方法的準確性和高效性，分別構造仿真案例予以說明。仿真過程中，采用MATLAB M語言實現該算法，使用的計算機中央處理器（CPU）為Intel 酷睿I5-4200M，主頻2.5GHz（最大睿頻3.1GHz），運行內存為4GB，操作系統為Windows 7 64位旗艦版。

3.1 準確性驗證仿真

首先，構造子數據段長度和幅值隨機的仿真數據，所構造數據的總長度為N=18000，數據趨勢如圖2 所示。將所構造的仿真數據看作是歷史數據X，為了驗證算法的有效性，以圖2 中是紅色數據段作為當前異常數據段XC，具體如圖3所示，將兩段綠色數據段設定為與紅色數據段高度相似的數據段。

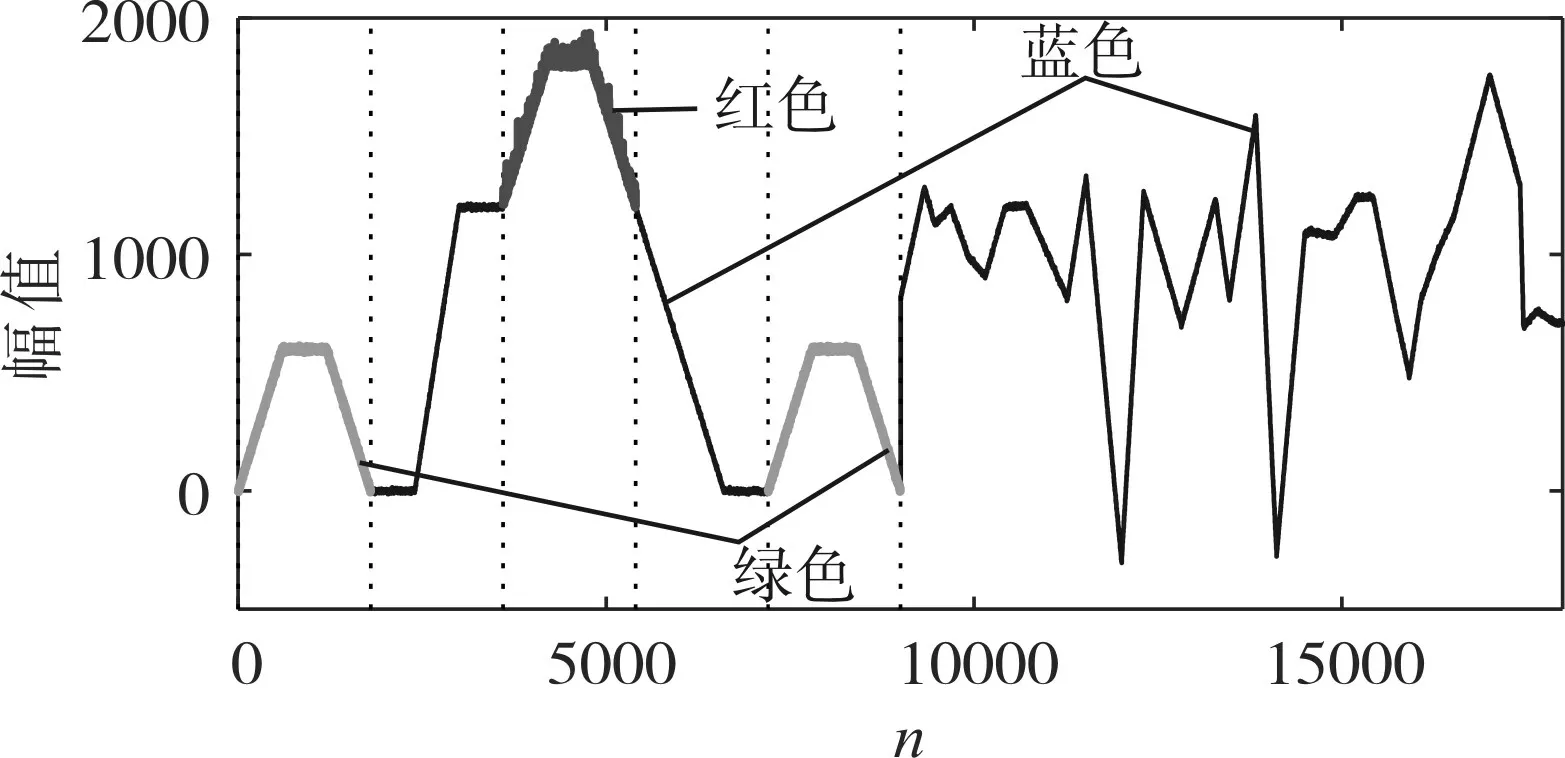
圖2 所構造的仿真數據趨勢曲線

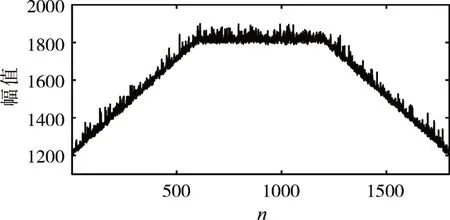
圖3 當前仿真數據圖

將仿真數據X與當前異常數據段XC二進制符號轉換，根據式（2）和式（3）對每個子序列X[i]的數值信息和趨勢信息分別進行符號轉換后進行合并，得到BC和B[i]。根據式（3）計算每個序列對(BC，B[i])之間的相關系數ρb(i)，設ε=0.7，按照該閾值篩選二進制子序列。依據所選的二進制子序列，提取仿真數據X對應的數據段形成候選集Cs。

依據式（6）計算候選集Cs中每個子數據段與XC的皮爾遜相關系數，且設定皮爾遜相關系數的閾值為0.99，選出最終相似的時間序列對，并按相似性數值進行降序排列。在此，選擇相似性最高的前三組作為最終選擇的數據段，結果如圖4 所示，其中圖4（a）為當前異常數據段XC本身，即圖2 中的紅色數據段，圖4（b）為圖4中的第二個綠色數據段，圖4（c）為圖4中的第一個綠色數據段。

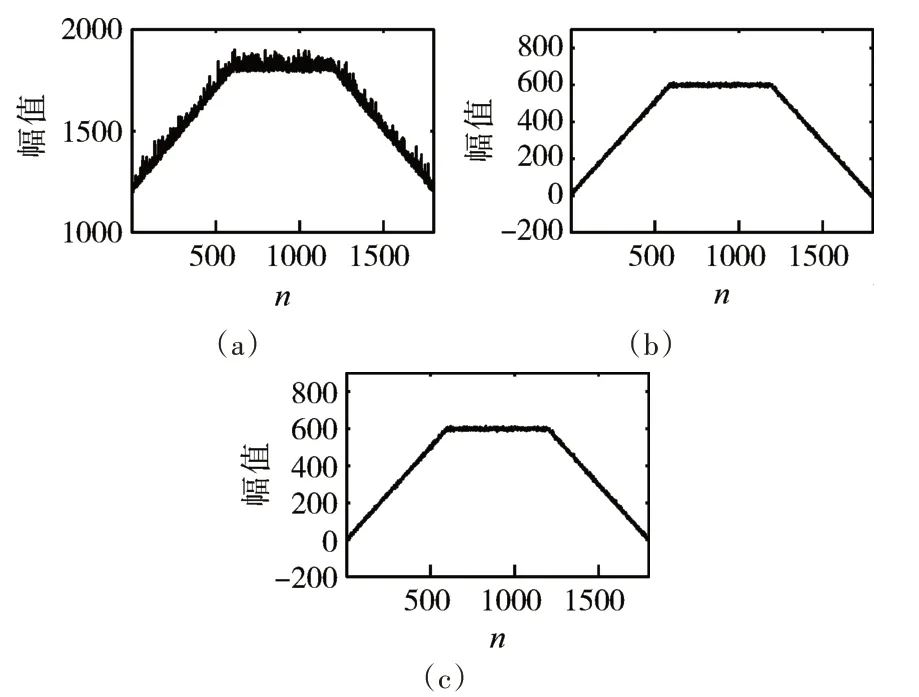
圖4 結果集中的時間序列對

由本仿真案例所查找到的相似數據段和仿真數據段的設計結構可知，本文所述的方法能夠準確查找出相似數據段。

3.2 高效性仿真驗證

為了驗證所述方法的高效性，在此通過構造不同長度的仿真數據，分別以本文所述方法和皮爾遜相關系數直接查找相似數據段方法做耗時對比驗證，結果如表1所示。

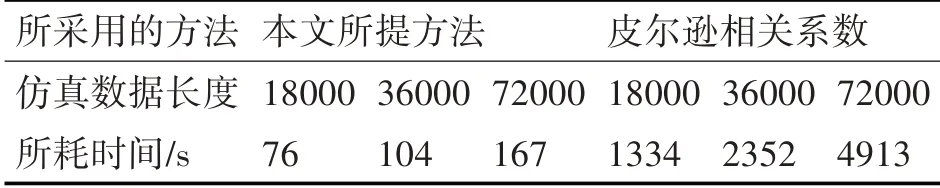
表1 所提方法與皮爾森相關系數的效率比較

通過對比仿真結果可知，在相同標準下，本文所述的方法在查詢速度上有大幅度提高。

4 結語

當前新能源大規模并網條件下，電網需要在多類型機組協調下運行，火電機組對電網多類型機組協調發揮至關重要的作用。在該背景下，本文研究了用以機組運行異常根源診斷的歷史數據相似數據段查找技術。通過計算當前異常數據段與原過程數據的二進制相似系數，形成目標數據集，進而通過皮爾遜相關系數查找目標數據集中與當前異常數據段高度相似的異常數據段，實現相似數據段查找的目的。通過仿真表明，該方法具有良好的準確性和高效性，對提火電機組運行水平以支撐電網多類型機組協調運行具有一定的意義。