一種水下探傷機(jī)器人動(dòng)力定位控制方法*

高宏博 戴曉強(qiáng) 趙 強(qiáng) 錢金偉 朱延栓

（江蘇科技大學(xué)電子信息學(xué)院 鎮(zhèn)江 212003）

1 引言

水下機(jī)器人（Remotely Operated Vehicle，ROV）在水下作業(yè)過(guò)程中，探傷儀等工具動(dòng)作會(huì)引起自身動(dòng)力學(xué)模型參數(shù)發(fā)生變化［1］，其本體也會(huì)受到作用力影響。這種由于模型參數(shù)變化引起的動(dòng)力定位控制精度問題，將直接導(dǎo)致探傷ROV 作業(yè)過(guò)程穩(wěn)定性能差、工作效率低。

針對(duì)上述問題Hussain 等［2］運(yùn)用自適應(yīng)控制和RBF 神經(jīng)網(wǎng)絡(luò)控制相結(jié)合的方法實(shí)現(xiàn)ROV 控制系統(tǒng)設(shè)計(jì)，并用仿真證明了系統(tǒng)具有良好的控制信號(hào)收斂性能和跟蹤性能。Heping Liu 等［3］利用神經(jīng)網(wǎng)絡(luò)逼近流體動(dòng)力學(xué)不確定性和擾動(dòng)上限，通過(guò)艏向控制測(cè)試證明了該控制策略的可行性。Li JH 等［4］提出了一種自適應(yīng)神經(jīng)網(wǎng)絡(luò)控制方法，通過(guò)神經(jīng)網(wǎng)絡(luò)對(duì)不確定擾動(dòng)進(jìn)行近似估計(jì)，證明了俯仰運(yùn)動(dòng)過(guò)程中的穩(wěn)定性，但是反步法設(shè)計(jì)過(guò)程中存在控制量導(dǎo)數(shù)階數(shù)過(guò)高，計(jì)算量太過(guò)復(fù)雜。王開紅等［5］基于滑模變結(jié)構(gòu)算法設(shè)計(jì)一種水下機(jī)器人控制系統(tǒng)，利用神經(jīng)網(wǎng)絡(luò)對(duì)滑模趨近率在線調(diào)整，但未考慮外部環(huán)境干擾等問題且收斂速度較慢。

鑒于以上研究基礎(chǔ)本文首先建立探傷ROV 六自由度運(yùn)動(dòng)模型，并在機(jī)械手展開前后引起的ROV 動(dòng)力學(xué)模型變化進(jìn)行分析；其次給出逼近模型參數(shù)不確定性的神經(jīng)網(wǎng)絡(luò)具體公式，再次設(shè)計(jì)自適應(yīng)滑模控制器，對(duì)控制參數(shù)在線調(diào)整，最后在李雅普諾夫穩(wěn)定性理論下證明系統(tǒng)漸近穩(wěn)定。通過(guò)對(duì)本文研制的探傷ROV 進(jìn)行水池動(dòng)力定位實(shí)驗(yàn)以及金山湖空間運(yùn)動(dòng)實(shí)驗(yàn)，驗(yàn)證了本文方法的有效性。

2 ROV動(dòng)力學(xué)模型

以江蘇科技大學(xué)自主研發(fā)的開架式水下探傷ROV 作為研究對(duì)象，建立坐標(biāo)系，如圖1所示，選擇水下探傷機(jī)器人的質(zhì)心作為載體坐標(biāo)系原點(diǎn)。定義水下探傷ROV運(yùn)動(dòng)參數(shù)，如表1所示。

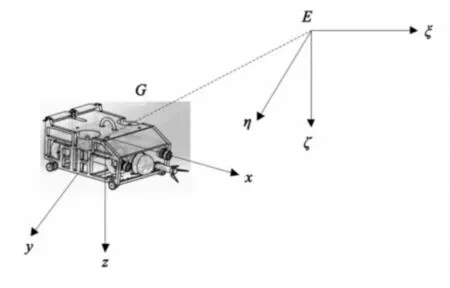
圖1 載體坐標(biāo)系示意圖

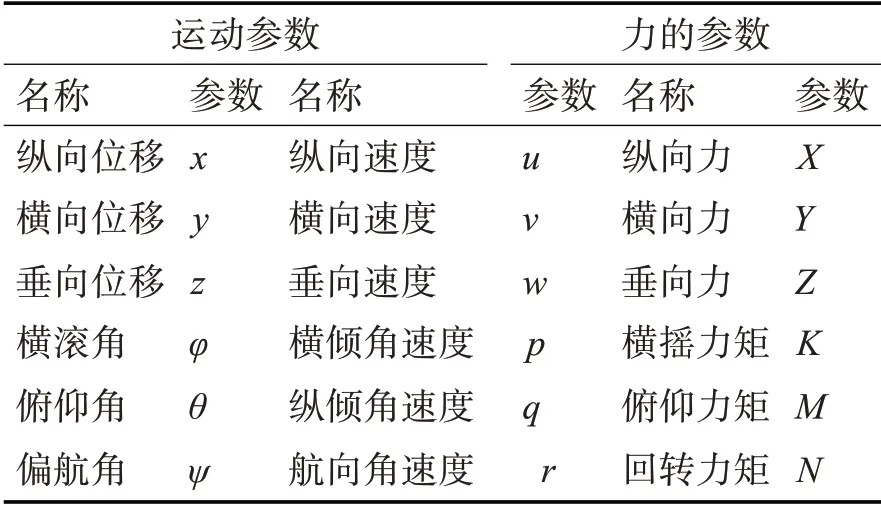
表1 參數(shù)定義

在實(shí)際運(yùn)動(dòng)過(guò)程中，水下機(jī)器人動(dòng)力學(xué)模型可用如下表達(dá)式描述：

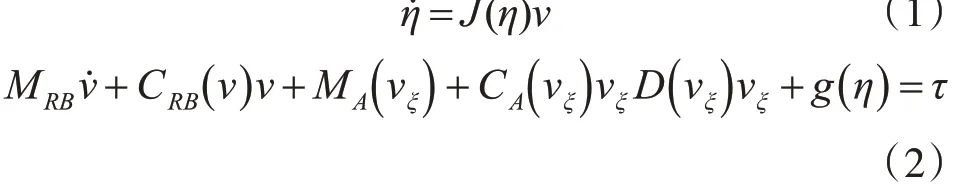
其中η=[x y z φ θ ψ]T，為地理坐標(biāo)系下ROV位置和姿態(tài)角；v=[u v w p q r]T，為ROV 速度矢量；，為坐標(biāo)轉(zhuǎn)換矩陣；MRB為ROV 慣性矩陣，MRB∈R6×6；CRB(v)為科氏向心力矩陣，CRB(v)∈R6×6；MA為外力作用引起的附加慣性矩陣，MA∈R6×6；CA為外力擾動(dòng)下的科氏向心力矩陣，CA(vξ)∈R6×6；D(vξ)為ROV 流體阻力矩陣，D(vξ)∈R6×6；g(η)為 回 復(fù) 力 矩 陣，g(η)∈R6×1；τ為ROV推進(jìn)器提供的推力，τ∈R6×1。

考慮機(jī)械手展開過(guò)程導(dǎo)致的模型參數(shù)不確定項(xiàng)和水流、波浪等未知干擾項(xiàng)帶來(lái)的影響［6］。假設(shè)ξ為環(huán)境干擾力，ξ∈R6×1，vd為地理坐標(biāo)系下伴隨干擾力產(chǎn)生的速度，vξ=v-vd，此處假設(shè)vd為慢時(shí)變的，滿足? ≈0，且C(v)=CRB+CA，則ROV實(shí)際動(dòng)力學(xué)模型應(yīng)調(diào)整為

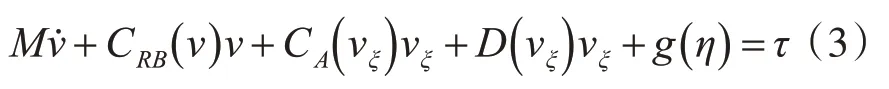
水下探傷ROV 重心xG=yG=zG=0，模型中的慣性矩陣M為

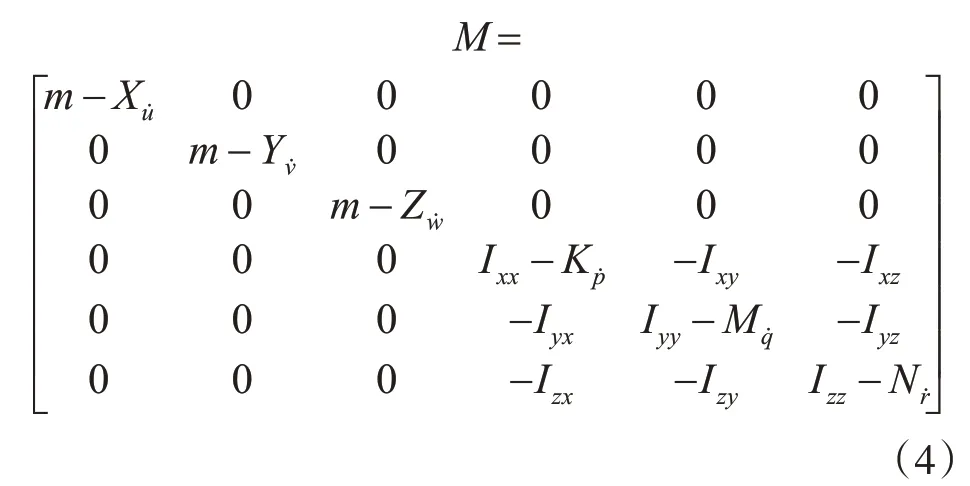
C(v)由科里奧利向心力以及附加質(zhì)量矩陣構(gòu)成，表示為

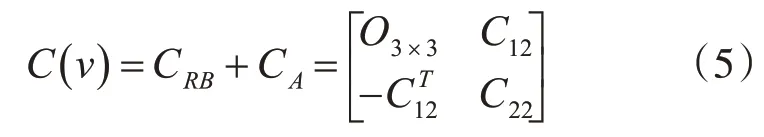
式中：

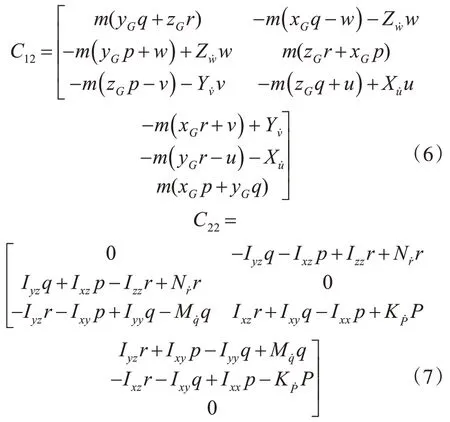
流體阻尼力矩陣D(v)表示為

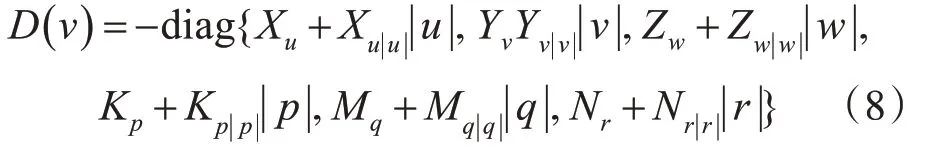
回復(fù)力矩陣g(η)表示為

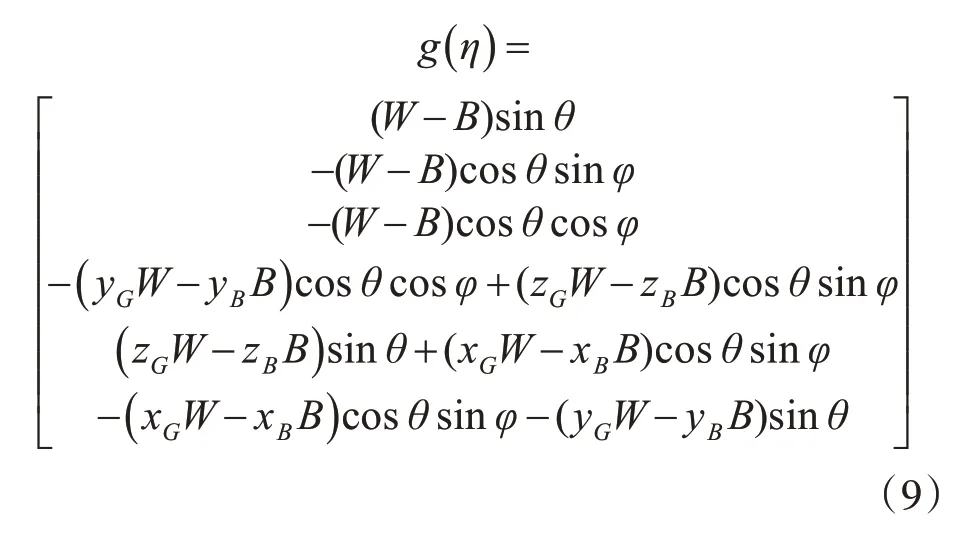
式中，W、B分別為水下探傷ROV 的重力和浮力，xB、yB、zB為浮心。

通過(guò)對(duì)機(jī)械手作業(yè)前后的ROV 系統(tǒng)動(dòng)力學(xué)模型解耦［7］，得到水下探傷機(jī)器人在單個(gè)自由度方向上的動(dòng)力學(xué)模型，在地理坐標(biāo)系中表示為

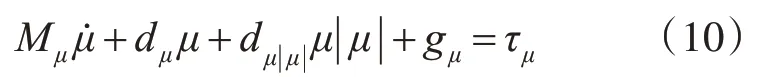
式中，Mμ為慣性系數(shù)，μ為ROV 速度矢量，dμ及dμ||μ表示阻尼常數(shù)，gμ表示ROV 豎直方向上的合力分量，τμ表示ROV 在運(yùn)動(dòng)方向上推進(jìn)系統(tǒng)提供的動(dòng)力。

3 ROV動(dòng)力定位控制方法

3.1 RBF網(wǎng)絡(luò)自適應(yīng)滑模控制方法研究

針對(duì)水下探傷機(jī)器人作業(yè)過(guò)程中因波浪干擾和機(jī)械手動(dòng)作引起的ROV模型參數(shù)不確定性［8］，進(jìn)而導(dǎo)致的動(dòng)力定位控制精度差等問題，提出一種RBF神經(jīng)網(wǎng)絡(luò)自適應(yīng)滑模控制方法，在李雅普諾夫穩(wěn)定性定理下證明本文提出的控制方法收斂穩(wěn)定。

3.1.1 建立狀態(tài)空間表達(dá)式

在地理坐標(biāo)系下姿態(tài)跟蹤誤差x1、x2，η為ROV當(dāng)前時(shí)刻姿態(tài)信息，ηd為期望姿態(tài)矢量，有如下表達(dá)式：

將ROV 動(dòng)力學(xué)模型轉(zhuǎn)換為2 階非線性被控對(duì)象，通過(guò)該狀態(tài)空間表達(dá)式可將ROV 模型中的不確定性部分和外界干擾構(gòu)成未知項(xiàng)函數(shù)［9~11］，方便下一步滑模面設(shè)計(jì)和RBF神經(jīng)網(wǎng)絡(luò)在線逼近。

根據(jù)式（1）、（2）、（11）、（12），建立如下非線性不確定系統(tǒng)的狀態(tài)方程：

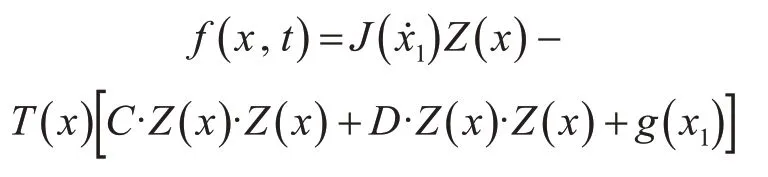
式中：

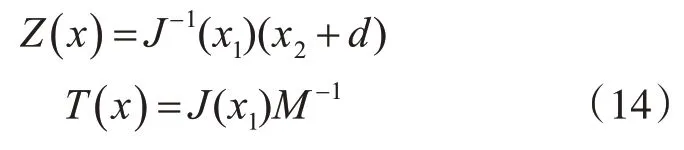
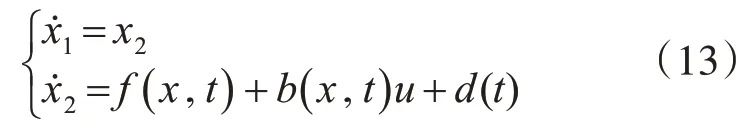
3.1.2 RBF網(wǎng)絡(luò)在線逼近模型參數(shù)和外界干擾

在ROV 實(shí)際作業(yè)過(guò)程中，存在輔助工具動(dòng)作引起的參數(shù)不確定項(xiàng)f(x，t)和其他因素d(t)，包括水流、風(fēng)浪等未知不定項(xiàng)。將f(x，t)、d(t)構(gòu)成不定項(xiàng)集合并用F(x，t)表示，通過(guò)神經(jīng)RBF 網(wǎng)絡(luò)對(duì)F(x，t)進(jìn)行在線逼近［12］。其中F(x，t)如下表示：

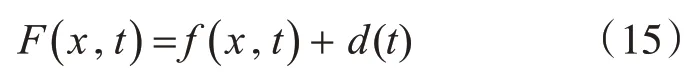
采用RBF神經(jīng)網(wǎng)絡(luò)逼近F(x，t)，表示為

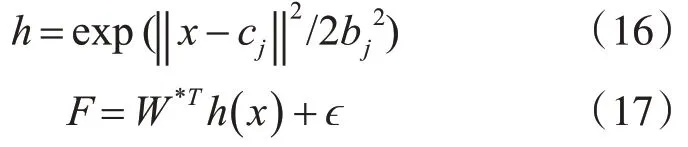
式中，W*T為網(wǎng)絡(luò)理想權(quán)值；?為網(wǎng)絡(luò)逼近誤差。

為了使RBF神經(jīng)網(wǎng)絡(luò)更好地進(jìn)行學(xué)習(xí)，采用梯度下降方法分別對(duì)輸出權(quán)值等參數(shù)進(jìn)行迭代［13~14］，網(wǎng)絡(luò)的學(xué)習(xí)算法表示為

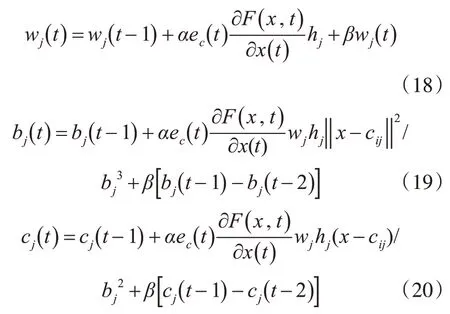
3.1.3 滑模控制器和自適應(yīng)律設(shè)計(jì)

設(shè)計(jì)滑模面［15~16］為

其中，e=x1-xd為系統(tǒng)跟蹤的實(shí)時(shí)誤差；e?=x2-x?d為變化率；c＞0 且為常數(shù)。

將本文設(shè)計(jì)的滑模面進(jìn)行求導(dǎo)，同時(shí)將ROV模型轉(zhuǎn)換得到的狀態(tài)空間方程帶入該式得：

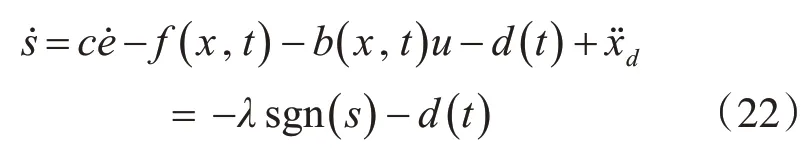
設(shè)計(jì)滑模控制率為

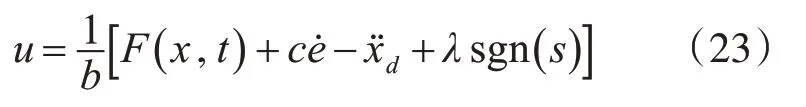
將式（23）帶入式（22）可得：

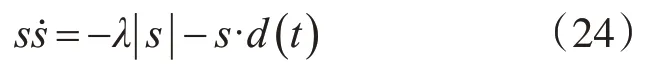
存在 |d(t)|≤D，λ≥D，使得ss?≤0。

RBF 神經(jīng)網(wǎng)絡(luò)的輸出為F?=W?Th(x)，帶入式（22）、式（23）可寫為

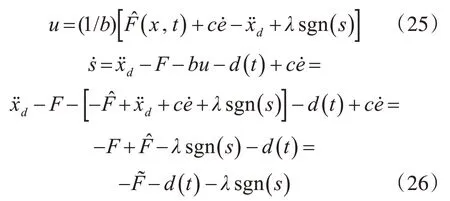
式中：

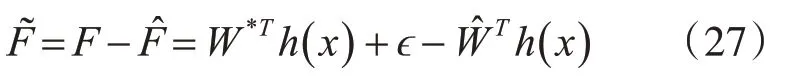
3.2 穩(wěn)定性證明

選取Lyapunov函數(shù)為

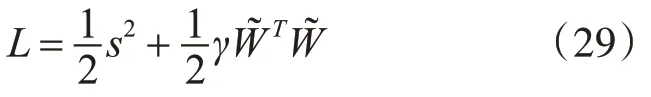
對(duì)L求導(dǎo)，并將?和滑模控制律帶入得：

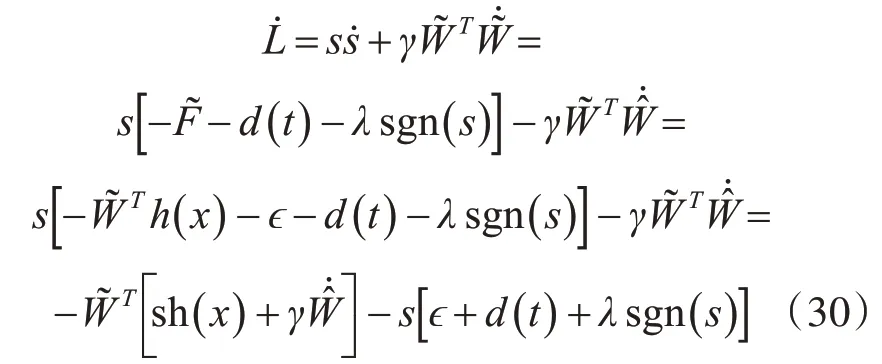
將自適應(yīng)律帶入式（30）得：

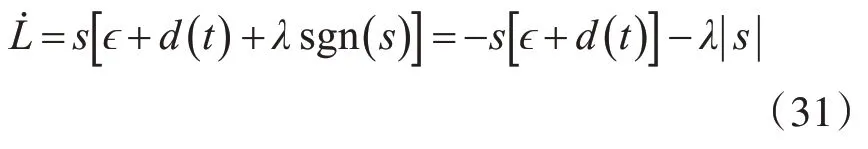
在RBF 網(wǎng)絡(luò)逼近過(guò)程中，?可以足夠小，取λ≥?0+D。存在λ0＞0，λ≥λ0+?0+D，使得：

由于L≥0，L?≤0，根據(jù)李雅普諾夫穩(wěn)定性理論可知，ROV 動(dòng)力定位控制系統(tǒng)的跟蹤誤差全局漸進(jìn)穩(wěn)定，并且滑模面和自適應(yīng)律一致穩(wěn)定有界，證明完畢。

4 實(shí)驗(yàn)驗(yàn)證

4.1 ROV樣機(jī)和測(cè)試環(huán)境

本文ROV 樣機(jī)如圖2 所示，測(cè)試環(huán)境如圖3 所示。

圖2 水下機(jī)器人系統(tǒng)及ROV樣機(jī)

圖3 水池實(shí)驗(yàn)

其中ROV 樣機(jī)為開架式結(jié)構(gòu)，實(shí)驗(yàn)水池長(zhǎng)5m、寬5m、深5m，通過(guò)手動(dòng)施加干擾模擬實(shí)際環(huán)境中水流波浪。

4.2 對(duì)比實(shí)驗(yàn)

探傷ROV系統(tǒng)參數(shù)見表2~3。

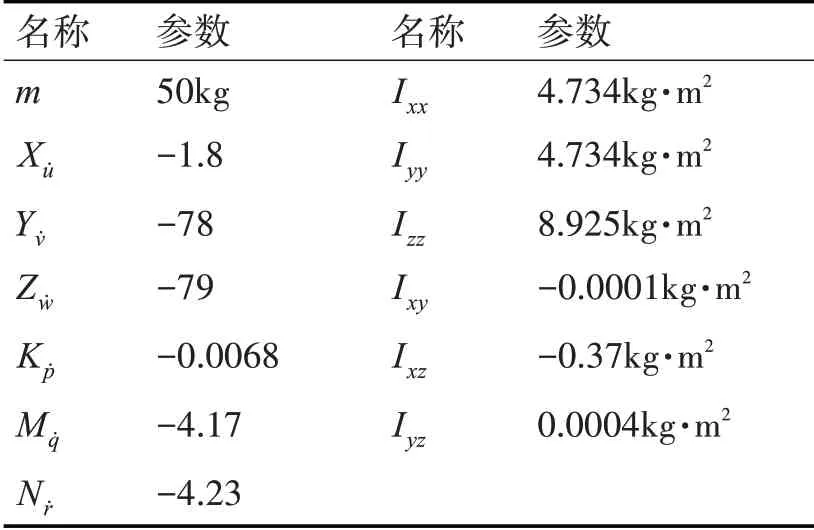
表2 慣性參數(shù)

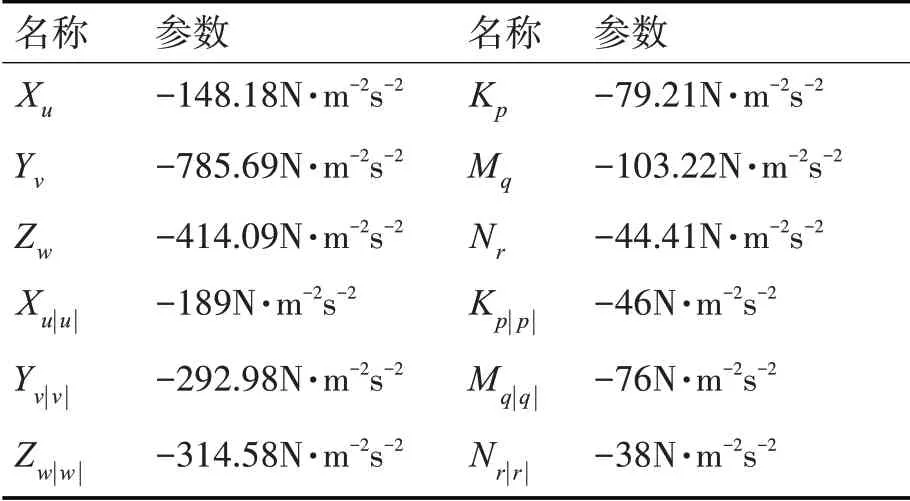
表3 阻尼系數(shù)

探傷ROV 作業(yè)過(guò)程中的主要干擾因素是水流和波浪，通常采用PM譜對(duì)其進(jìn)行分析［17］。

采用如下表達(dá)式描述波浪運(yùn)動(dòng)情況：

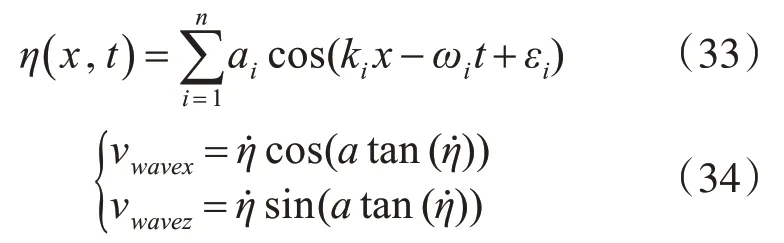
式（33）、式（34）中，vwavex、vwavez表示波浪在水平和垂向兩個(gè)自由度上的速度。

4.2.1 艏向、垂向運(yùn)動(dòng)控制實(shí)驗(yàn)驗(yàn)證

分別在平穩(wěn)環(huán)境和存在外部擾動(dòng)情況下，對(duì)艏向上的目標(biāo)軌跡ψ=10 sin( 0.015πt)+50 進(jìn)行跟蹤，實(shí)驗(yàn)結(jié)果如圖4、5所示。

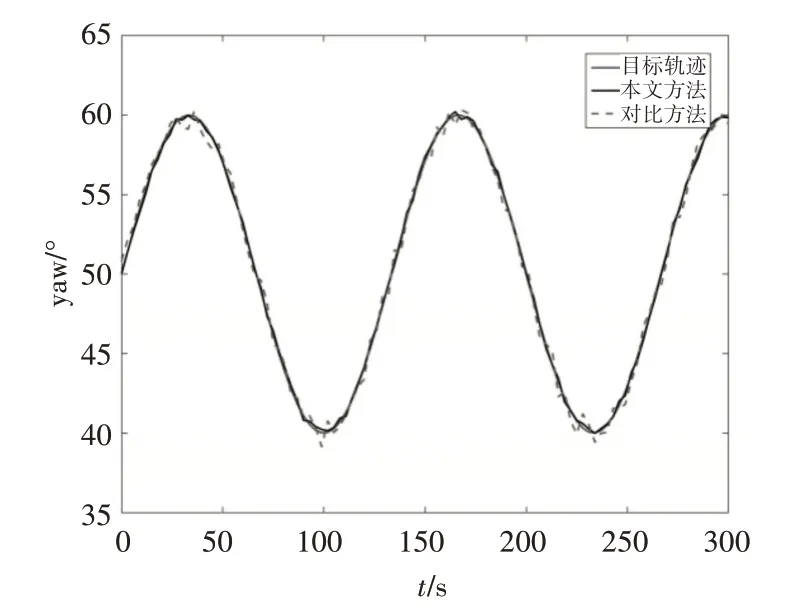
圖4 無(wú)干擾下艏向跟蹤曲線

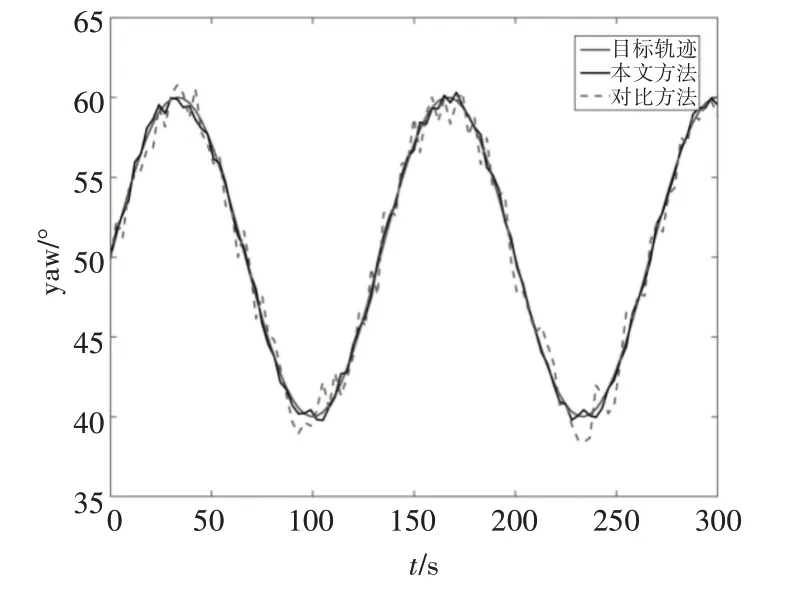
圖5 波浪干擾下艏向跟蹤曲線

分別在平穩(wěn)環(huán)境和存在外部擾動(dòng)情況下，在垂向上對(duì)預(yù)先設(shè)定的深度軌跡進(jìn)行跟蹤，其目標(biāo)軌跡表達(dá)式為H=0.1 sin( )0.03πt+2，實(shí)驗(yàn)結(jié)果如圖6、7所示。

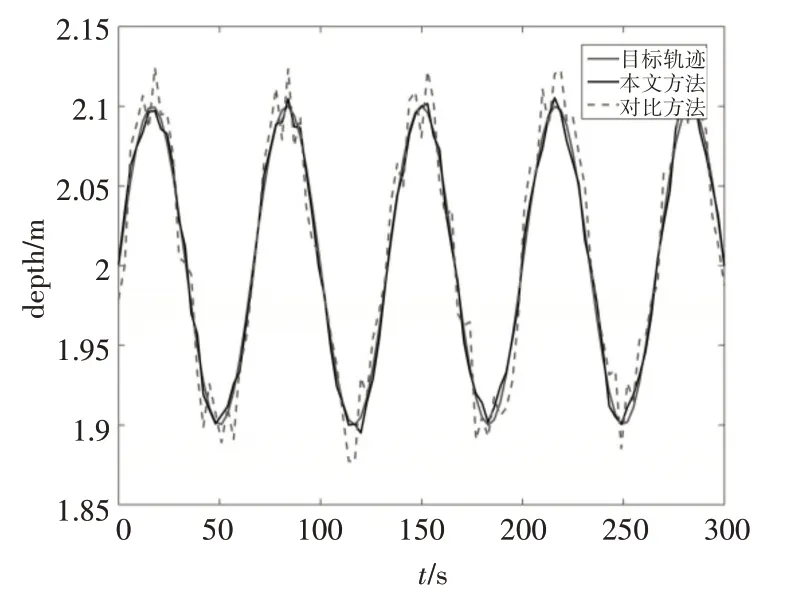
圖6 無(wú)干擾下垂向跟蹤曲線

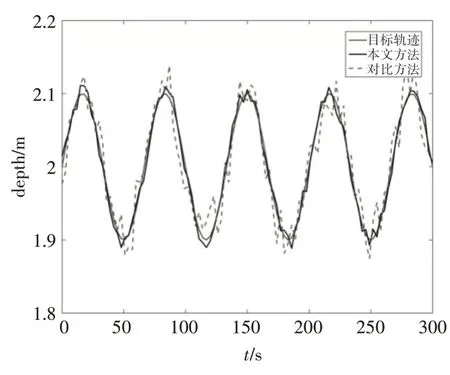
圖7 波浪干擾下垂向跟蹤曲線

水下機(jī)器人在水池內(nèi)的水平方向做轉(zhuǎn)艏及豎直方向做升降運(yùn)動(dòng)，能夠按照設(shè)定的軌跡運(yùn)動(dòng)并到達(dá)指定位置。水池測(cè)試實(shí)驗(yàn)結(jié)果如表4所示。

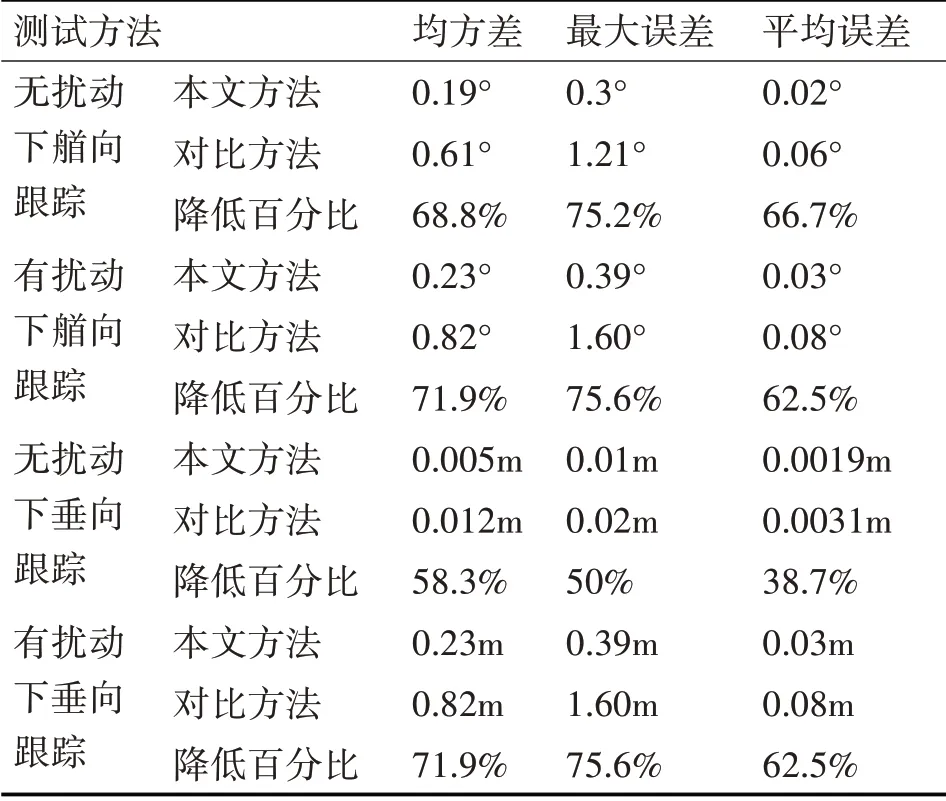
表4 誤差數(shù)據(jù)對(duì)比

在艏向上對(duì)目標(biāo)軌跡進(jìn)行跟蹤，通過(guò)RBF神經(jīng)網(wǎng)絡(luò)對(duì)波浪擾動(dòng)的干擾函數(shù)進(jìn)行在線逼近。存在擾動(dòng)情況下，本文控制方法誤差均方差、最大誤差及平均誤差分別為0.23°、0.39°、0.03°，對(duì)比傳統(tǒng)自適應(yīng)滑模控制方法誤差百分比分別降低71.9%、75.6%、62.5°。在對(duì)垂向軌跡進(jìn)行跟蹤，本文控制方法誤差均方差0.0078m，相比于傳統(tǒng)自適應(yīng)滑模控制方法降低76.4%，最大誤差為0.015m，相比于傳統(tǒng)自適應(yīng)滑模控制方法降低72.2%，平均誤差為0.0021m，相比于傳統(tǒng)自適應(yīng)滑模控制方法降低60.4%。實(shí)驗(yàn)數(shù)據(jù)結(jié)果表明，本文動(dòng)力定位控制方法的效果明顯優(yōu)于傳統(tǒng)自適應(yīng)滑模控制方法。

4.2.2 金山湖定點(diǎn)動(dòng)力定位實(shí)驗(yàn)

水池內(nèi)完成基本運(yùn)動(dòng)控制實(shí)驗(yàn)后，在金山湖完成空間內(nèi)動(dòng)力定位實(shí)驗(yàn)，空間內(nèi)軌跡跟蹤如圖8 所示。

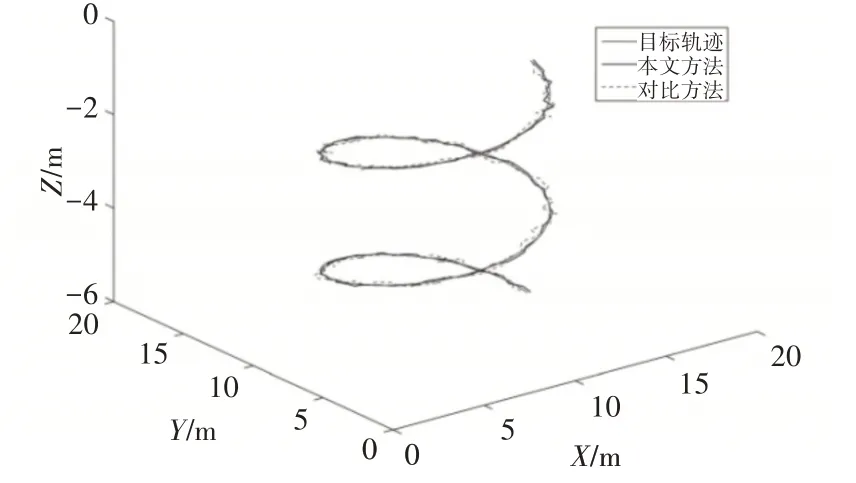
圖8 動(dòng)力定位軌跡

5 結(jié)語(yǔ)

針對(duì)ROV 在實(shí)際過(guò)程中的作業(yè)精度與魯棒性需求，并考慮外部擾動(dòng)引起的模型參數(shù)不確定性問題，提出了一種RBF 神經(jīng)網(wǎng)絡(luò)自適應(yīng)滑模控制策略，通過(guò)RBF神經(jīng)網(wǎng)絡(luò)對(duì)波浪擾動(dòng)的干擾函數(shù)進(jìn)行在線逼近，解決了傳統(tǒng)自適應(yīng)滑模控制在ROV 動(dòng)力定位過(guò)程中軌跡跟蹤精度低和對(duì)外部干擾敏感的問題。最后通過(guò)實(shí)驗(yàn)結(jié)果表明，相比較傳統(tǒng)自適應(yīng)滑模控制方法，本文所提出的動(dòng)力定位控制方法定位誤差小、魯棒性能好。