基于北斗三號的高速公路壓實監測應用

邵沛涵，王志斌，高成發，張 博,郝文世，高 平

(1.東南大學 交通學院，南京 211189;2.河北雄安京德高速公路有限公司,河北 保定 071799)

北斗衛星導航系統(BeiDou Navigation Satellite System，BDS)是我國自主研發的全球定位系統，結合我國國情形成了“三步走”發展戰略[1]。2020年6月23日北斗三號全球衛星導航系統(BDS-3)的最后一顆全球組網衛星發射成功并于2020年7月31日正式宣布開通。對于MEO衛星，BDS-3不僅能夠提供兼容BDS-2的頻率(B1I和B3I)，還增加了B1c和B2a兩個信號[2]，能夠兼容GPS(L5)和Galileo(E5a)，以便于實現系統間的兼容互操作。同時，BDS-3相對于BDS-2在衛星星座和信號設計方面有大幅改進并使用新的氫原子鐘，多路徑效應明顯減弱[3]。因此，BDS-3的全面建成必將帶來定位精度和穩定性的進一步提高。

與傳統監測手段相比，GNSS測量具有高精度、全天候實時監測、工作效率高、人工需求小、測站間無需通視、可提供全球統一的三維地心坐標等特點。王世進等人對GPS/BDS的RTK定位算法進行研究分析[4]，結果表明GPS/BDS的RTK定位精度能夠達到cm級，且模糊度固定時間相對于單系統明顯減少。隋春玲等人分析GPS/GLONASS/BDS組合的單歷元單頻短基線RTK定位精度[5]，在NEU3個方向上的精度均達到mm級；王藝希等人[6]利用附帶參數的卡爾曼濾波方法，計算得到31 km基線條件下，NE方向定位誤差在1 cm以內，U方向誤差在3 cm以內。綜上，由于設計規范規定的分層厚度為亞米級，RTK能夠滿足精度需求，為數字化施工提供有利條件。

文中采用的方案是在壓路機頂部安裝GNSS接收機、在工程項目部安裝GNSS基站(兩者相距不超過15 km)，使用附帶參數的卡爾曼濾波模型進行RTK定位，實時采集地面點坐標，并和現場水準測量結果進行對比，分析RTK定位的精度和層厚計算的準確性。

1 GNSS-RTK算法

1.1 雙差函數模型

文中以GPS和BDS組合定位為例，其雙差偽距和載波相位觀測方程[7-8]為：

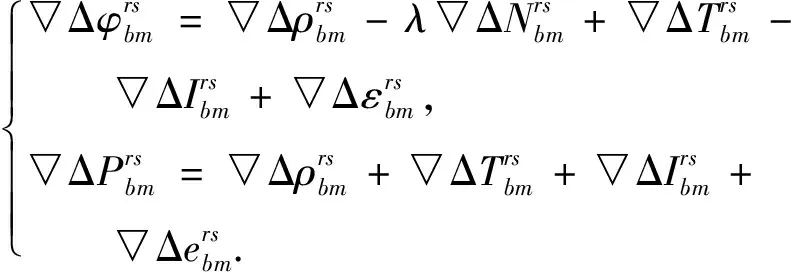
(1)

式中:r和s分別代表參考衛星和差分衛星;b和m分別代表基準站和流動站;φ和P表示以m為單位的載波和偽距觀測量;ρ表示衛星到接收機的距離;λ和N表示對應頻率載波的波長和模糊度;T和I表示對流層和電離層延遲;ε和e表示偽距和相位的觀測噪聲等其他誤差。

將上述載波觀測方程寫成誤差方程并進行線性化，可得：

(2)

其中，

(3)

(4)

偽距誤差方程線性化同理，定權時偽距和載波權重按照1∶1 000。GPS和BDS組合定位模型可在各系統內部選擇參考衛星進行雙差，再組合不同系統的雙差觀測值來求解基線向量。利用組合模型進行RTK解算可以將各系統的衛星數據都進行應用，并認為系統之間互不相關。

1.2 隨機模型

文中采用基于高度角的隨機模型，即將觀測值噪聲σ表達成以衛星高度角E為變量的函數[9]。已有研究表明，高度角定權法比單位權法得到的數據精度有明顯提高，且在衛星數量較少時尤為明顯[10]。下面簡述定權過程：

當考慮到電離層、對流層延遲影響與高度角的比例關系時[11]，可以定義一種正弦函數模型。若選擇衛星r作為觀測歷元ti的參考衛星，則衛星s的雙差觀測值的噪聲可表示為：

(5)

式中：Er和Es分別為參考衛星r和衛星s的高度角。

若歷元ti中共有n顆衛星，則會構成n-sys個觀測方程，sys為使用的衛星系統個數，根據誤差傳播定律，則方差-協方差陣可表示為：

(6)

1.3 附帶參數的卡爾曼濾波模型

將線性化后的誤差方程簡化為：

V=BX-L.

(7)

由于文中采用的實測數據采樣間隔為1.0 s，故對于動態RTK定位宜采用常加速度模型[12]，則式中的X即狀態向量可以描述為：

X=[xpos，ypos，zpos，xvel，yvel，zvel，xacc，yacc，zacc，

▽ΔN1，…，▽ΔNn-sys]T.

(8)

其中包含位置參數、速度參數、加速度參數和雙差模糊度參數。位置參數的初值可以用單點定位的結果，速度參數的初值可以根據多普勒觀測值計算得到，當多普勒觀測值不足時可根據實際情況設置一個經驗值，加速度初始值一般設置為零，模糊度參數初始值可由偽距和載波確定。

t(k)時刻卡爾曼濾波基本遞推過程如下[9,13]：

(9)

(10)

(11)

(12)

(13)

系統噪聲的方差-協方差陣Qk為：

Qk=

(14)

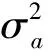
對于其初值，位置參數可賦予一個較大的方差，速度和加速度對應的方差較小，模糊度對應的方差較大。

狀態轉移矩陣Φk,k-1的設置如下：

(15)

通過附帶參數的卡爾曼濾波模型得到模糊度參數的浮點解，然后使用LAMBDA算法[14]進行固定，將固定解回代到觀測方程中即能得到基線向量的固定解。

2 基于GNSS數據的層厚計算算法

層厚計算可分為實時處理和后處理，兩者基本思路相同，區別是后處理時可以根據實際施工范圍和最后的壓實時間對所有坐標數據點進行約束，減少循環次數，從而提高計算效率。但考慮到施工現場的實際情況，一般壓實后不會馬上進行填土，實時處理時最后的壓實高度可認為和后處理時選取的時間相同，因此在實際計算時，實時處理和后處理效率基本相同。

2.1 實時處理

1)獲取實時坐標數據。通過RTK計算得到當前時刻t(k)的三維坐標數據Pk(xk,yk,zk)，并進行儲存。

2)從初始時刻t(0)開始以每個歷元的平面坐標為基準，建立縱向結構體Di(i=1，2，…，n)，該結構體包括分層數據。設置一定的閾值，當其他歷元的坐標落在該閾值以內時，認為是同一個縱向結構體。否則，新申請一個縱向結構體Di+1并將該點存入。

3)建立初始分層。判斷最先進入縱向結構體的5個歷元的高程坐標，剔除粗差后取平均值作為初始層高，建立初始分層結構體。

4)對每個新進入縱向結構體的三維坐標點Pk進行分層判斷，如果高程方向差值在給定閾值以內(根據施工規范一般設置為h1=25 cm左右為宜)，則將該點添加進這一分層結構體。否則，新申請一個分層結構體并將該點存入。需要注意的是，為避免粗差對分層造成較大影響，應設置高差的最大閾值(h2=35 cm)，該值可根據現場填土情況取一個經驗值，當超過該閾值時，認為不是填土造成的分層而是粗差，此時不應申請新的分層結構體。

5)重復上述步驟，逐歷元判斷。當存在兩層及以上分層結構體時，即可計算得出層厚。

2.2 后處理

1)根據先驗信息，設置施工區域的坐標范圍，根據時間截取需要處理的數據，從而減少數據量提高后處理速度。

2)劃分格網。地形起伏較大時格網邊長可設置小一些。

3)循環所有數據點，并判斷到格網中心點的距離，在閾值以內時將其加入到該格網結構體中。

4)根據時間最近原則生成所需數據，根據每個數據點到格網中心的距離取加權平均值作為格網的高程，具體算法如下：

(16)

5)生成三維地形數據。三維地形數據實時處理流程如圖1所示。

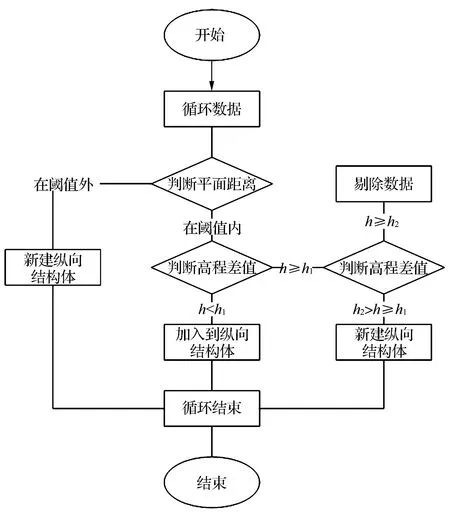
圖1 實時處理流程

3 測試方案及數據分析

3.1 測試方案

測試時，在路基上事先布設若干點(見圖2)，相鄰點間隔10 m左右，利用RTK測出點的平面坐標以便于后續放樣。從施工現場的高等級水準點出發，采用二等水準的方式將高程引入路基，并測量出布設點的高程，每次壓實后測量出真實高程，通過兩次高程相減得出層厚，并和利用壓路機實時數據計算的結果進行對比，以驗證文中所提方法的準確性。

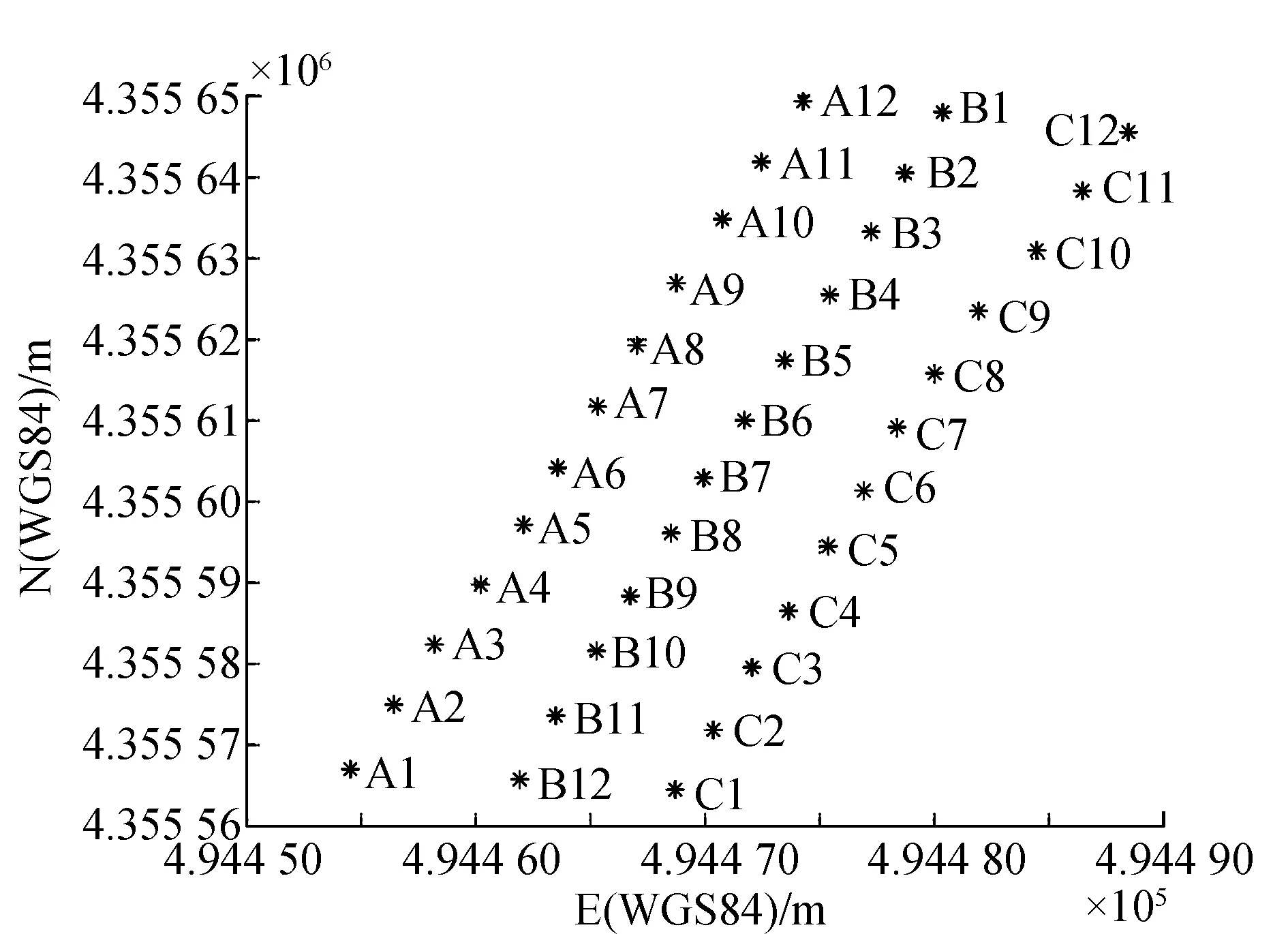
圖2 RTK點位布設示意圖

壓路機采集數據坐標系為WGS84坐標，水準測得的高程為施工坐標系，可通過Bursa七參數模型實現兩者的統一[15]。具體做法是首先采集3個及以上已知施工坐標的控制點的WGS84坐標，通過式(17)計算出七個參數，再利用七參數將壓路機采集的數據按式(18)實時進行坐標轉化。

(17)

(18)

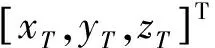
3.2 數據分析

文中使用的數據為“京德高速”現場實測數據，數據采集日期分別為2020年8月1日(年積日214)和2020年8月4日(年積日217)，這兩天分別進行兩次填土和壓實，如圖3、圖4所示。基站距離壓路機施工現場4.5 km左右。

圖3 施工現場示意圖

圖4 壓路機工作過程示意圖

3.2.1 BDS-3定位性能分析

文中在分析BDS-3的定位性能時，將原始觀測數據導出，分析GPS、BDS-2和BDS-3不同系統組合情況下，RTK定位時的模糊度固定成功率和U方向上的定位誤差(層厚計算對U方向的精度尤其重視)。圖5、圖6給出每個歷元下各系統衛星數量和對應的PODP值，其中PDOP數值越小衛星分布程度越好，定位精度越高。

圖5顯示每個歷元下BDS衛星數量已經遠超過GPS衛星數量，同時BDS-3衛星數量基本在4顆以上，可以滿足單BDS-3定位的需要，從圖6可以看出，只有GPS衛星或BDS-2衛星的情況下衛星的幾何分布不理想，同時也能看出即使BDS-2衛星數量比GPS衛星多的情況下有時PDOP值仍較大。但加入BDS-3衛星后整體PDOP值顯著減小，可見BDS-3空間結構優于BDS-2，同時GPS+BDS-2+BDS-3多系統的融合進一步增強衛星的幾何結構，使得PDOP值再次減小。

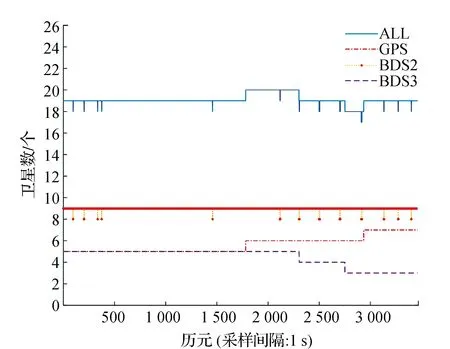
圖5 各系統衛星數

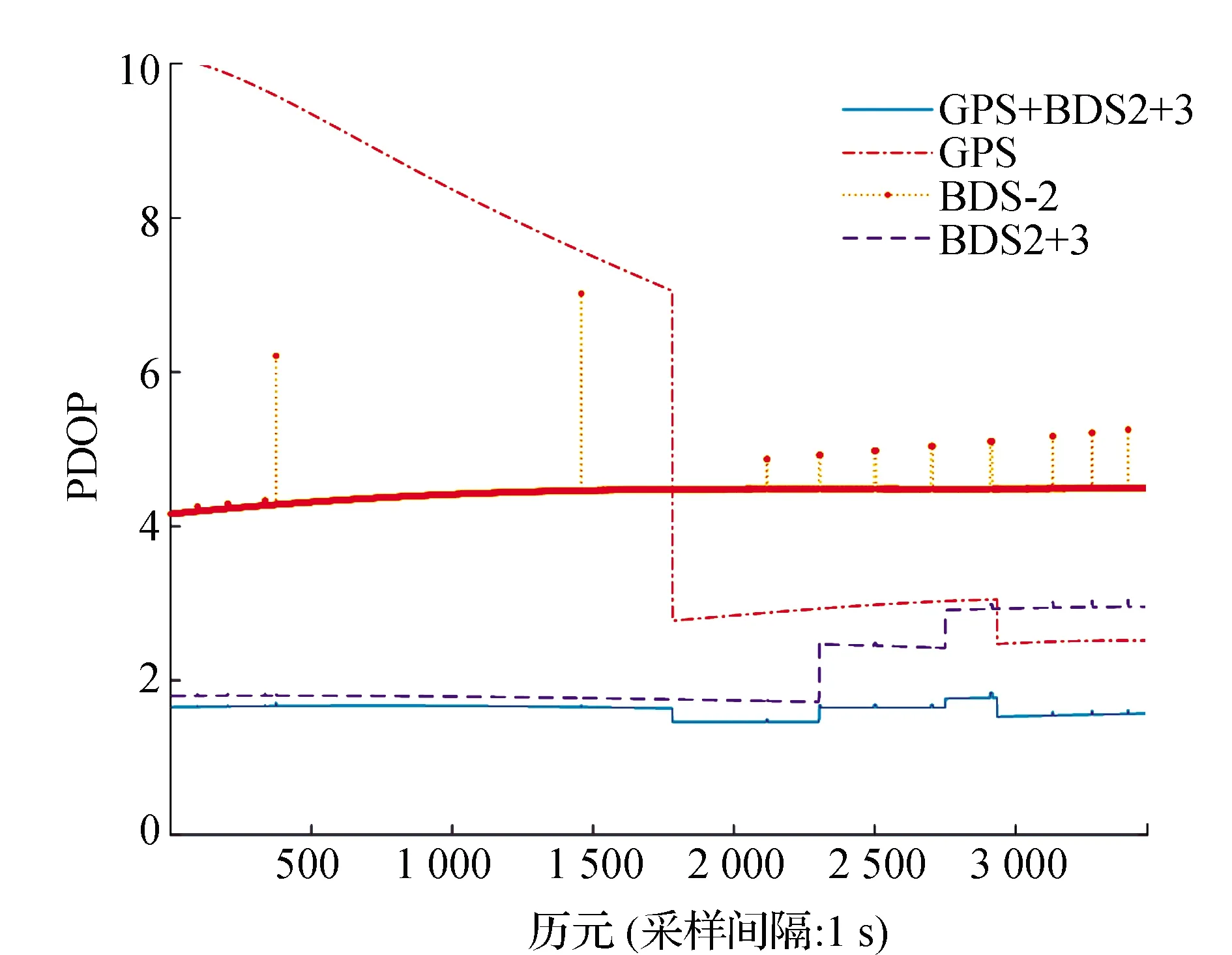
圖6 各系統PDOP統計

表1給出壓路機在施工區域工作時，在GPS、BDS-2和BDS-3不同系統組合情況下基線模糊度固定成功的歷元數和成功率，可以看出加入雙系統固定成功率比單系統成功率要高，且加入BDS-3后模糊度固定成功率得到了極大的改善。

表1 模糊度固定情況比較

由于層厚計算最關鍵的是U(高程)方向的定位誤差，在精度要求范圍內，可認為二等水準測量結果為真值，因此文中比較GPS、BDS-2和BDS-3不同系統組合情況下計算得到的高程和二等水準測量結果的差值，如表2所示。從表中可以看出，使用BDS定位時，高程方向誤差為cm級，能夠滿足層厚計算的精度要求。同時使用BDS-3定位相對于不使用在高程方向上的精度得到了明顯的提升。

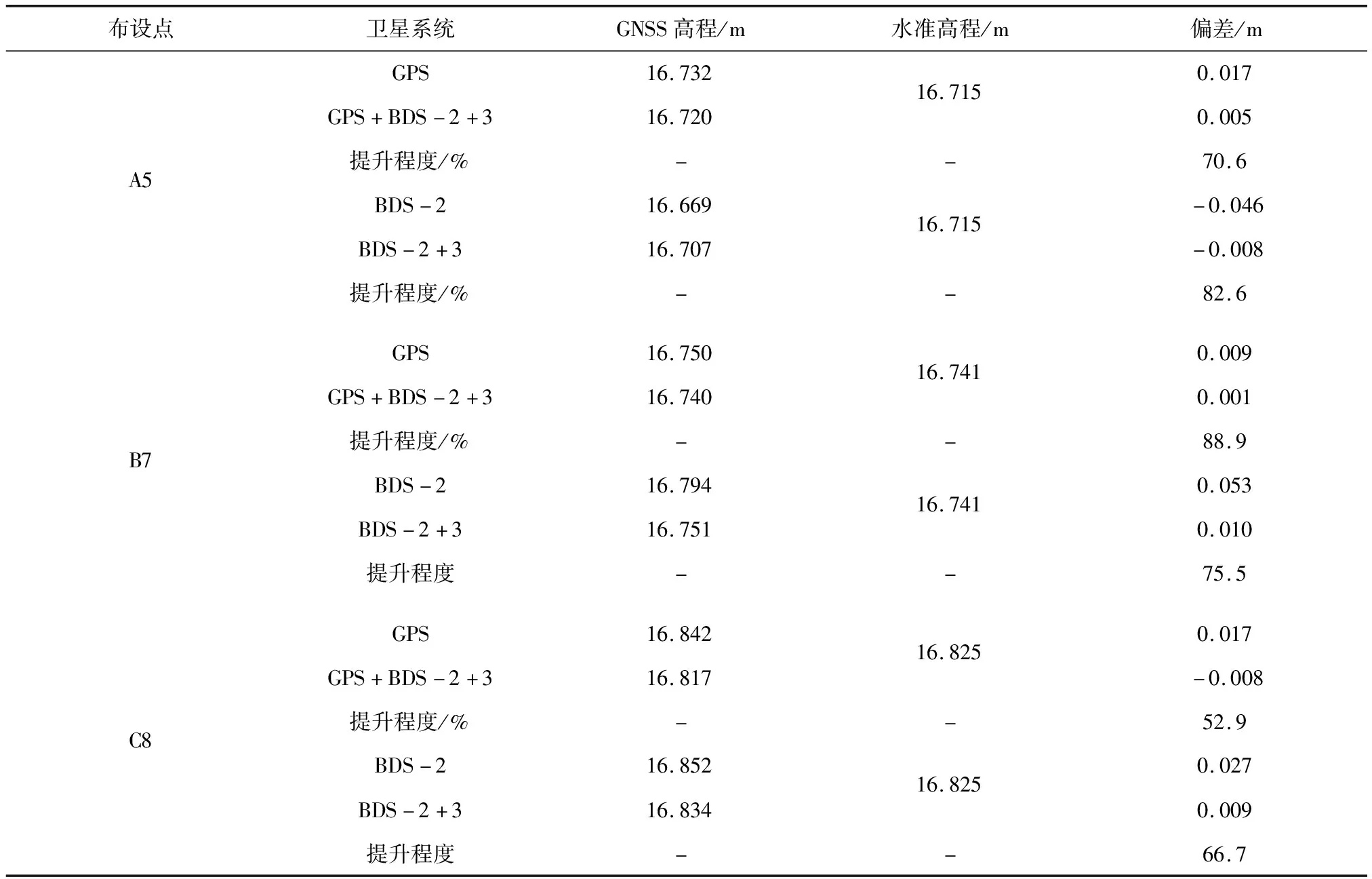
表2 定位結果比較

3.2.2 層厚計算

由上述分析可知，將GNSS-RTK技術應用于路基層厚計算中是可行的，通過壓路機采集的離散數據，可將施工現場劃分出若干格網(格網效果如圖7所示)，再通過內插和加權平均的方式，就可以計算得到施工現場任意點的高程坐標，兩次壓實后的高程相減就能得到任意點的層厚值。

圖7 格網效果(m)

文中分析2020年8月1日(年積日214)和2020年8月4日(年積日217)兩次填土后形成的新層的層厚，并和二等水準結果做比較(部分點如表3所示，整體結果如圖8所示)，結果顯示，GNSS計算的層厚值(平均值40.2 cm)和水準測量的層厚值(平均值40.3 cm)整體偏差在1 cm以內，因此文中提出的方法能夠準確地計算出層厚值。

圖8 層厚整體情況

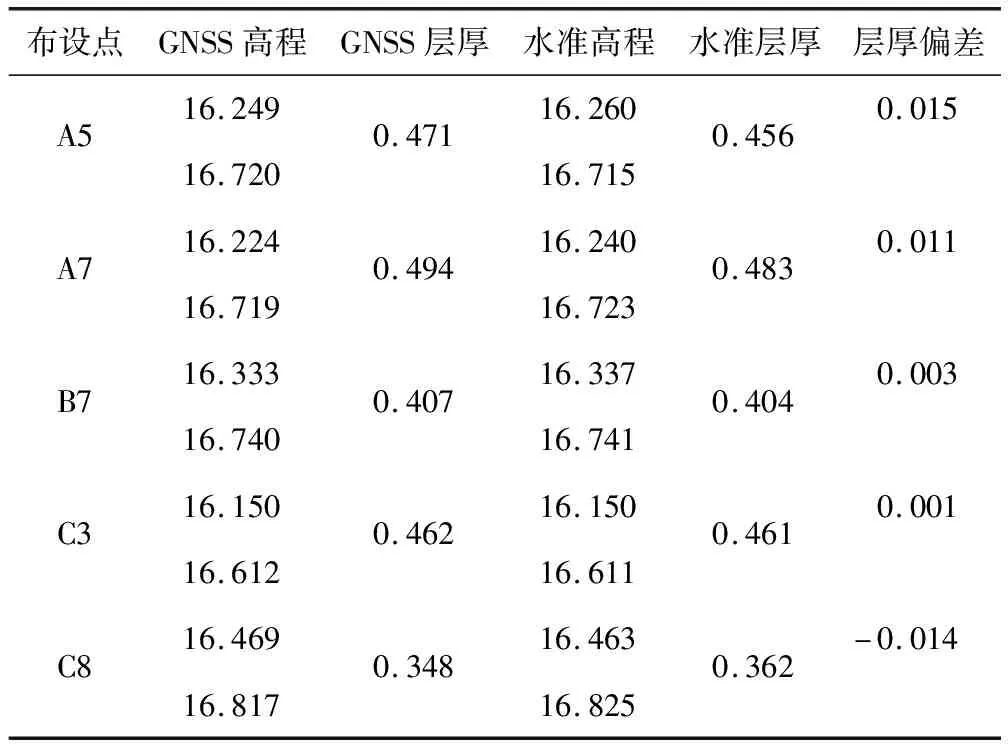
表3 層厚值比較 m

4 結束語

文中首先給出GNSS-RTK定位的函數模型和層厚計算的具體過程，分析比較GPS、BDS-2、BDS-3不同組合定位的精度，結果表明多系統定位在衛星空間結構和定位精度上均優于單系統，BDS-3相對于BDS-2的定位精度提升幅度較為明顯。在層厚計算最關注的高程方向精度，多系統定位能夠滿足實時計算的精度要求。

文中討論內容僅限于將GNSS應用于層厚計算，對于路基施工更關注的壓實度暫未涉及，有關GNSS+傳感器融合處理的內容仍需繼續研究。此外，對于BDS-3多頻，尤其是新增的幾個頻點的性能評估仍需持續分析。