基于高斯擴散模型的爆破粉塵可量化可視化研究

郭 堯

(1.中國礦業大學(北京) 力學與建筑工程學院， 北京 100083；2.海南省發展和改革委員會，海南 海口 570204)

爆破是鐵道工程中最基礎、最廣泛應用的技術之一，特別是隨著我國鐵路路網結構的基本建成，后續鐵路建設越來越多的面臨緊鄰既有線施工，爆破技術運用好壞直接關系到列車行車安全[1-2]。爆破過程除產生飛石和振動外，現階段也越來越關注爆破粉塵對列車行車安全的影響，粉塵不但阻斷接觸網的導電性，還遮擋駕駛員的視線。

目前國內在爆破粉塵防控方面已做了一些研究，但如何形成量化的可復制的防控方法研究較少[3-9]。已有研究主要為爆破煙塵運動階段劃分和各階段受力特征分析方面，沒有很好地與具體水霧降塵技術銜接，因此并未解決工程實際應用中各相關參數的設計問題，這影響了相關方法的深入研究和推廣應用。

高斯擴散模型具有較好的處理模糊性和隨機性的能力，是研究定性概念和定量數值轉換的數學模型[10-16]。為了解決上述問題，考慮爆破粉塵擴散的模糊性和隨機性，本文引入高斯擴散模型和Ansys Fluent軟件進行模擬計算。首先建立粉塵擴散的物理數學模型，然后采用Matlab和Ansys Fluent軟件模擬爆破粉塵擴散規律，得出爆破產塵量和爆破粉塵擴散范圍，給出爆破水霧降塵中水袋參數設置，最后以實例表明該方法的可行性和有效性。

1 爆破粉塵擴散模型建立及求解

1.1 模型假設

(1)爆破粉塵源屬于在一定爆破區域內，由地面固定位置連續排出的源。

(2)巖石爆炸及粉塵擴散過程時間短暫，爆區周圍氣象條件保持穩定。

(3)地表對粉塵無吸收和吸附作用。

1.2 模型建立

以爆區中心為原點，設水平下風方向為x軸，水平面垂直下風方向為y軸，垂直水平面方向為z軸，考慮濃度在y方向和z方向對稱并符合正態分布，可得濃度q分布為

(1)

式中：A(x)為點源排放強度函數；σy、σz分別為y、z方向的大氣擴散參數。

根據質量守恒定理，粉塵排放量應為下風方向所有粉塵的總和，即

(2)

將式(1)代入式(2)，可得無界情形下連續點源高斯擴散式為

(3)

爆源為一個區域，具有一定面積，可將式(3)沿x和y方向積分。同時，考慮地面這個界面的存在，濃度測試儀器架設于近地面，即z=0，可得

(4)

式中：QA為爆破粉塵面源排放量，kg/(m2·s)；a為爆破區域垂直于下風方向的長度，m；H為爆破源離地高度，m。

(5)

(6)

式(6)中x增大，則σy、σz隨之增大，即濃度q隨著距離x增大而減小，最大濃度qmax出現在x=0爆心處。

在一次爆破中，布置k個粉塵濃度測點，則粉塵面源排放量取算術平均值，即

(7)

爆破后經過時間t0，爆破粉塵源排放量Q為

Q=QA·t0·a·β

(8)

式中：t0為粉塵量采集時長，s；β為爆破區域平行于下風方向的長度，m。

根據爆破粉塵源排放量計算爆破粉塵排放強度W，可得

W=Q/T

(9)

式中：T為爆破總炸藥量，t。

1.3 模型求解

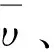
1.3.1 試驗方案

考慮爆破粉塵擴散主要受自然風影響，在距離爆破區域中心30 m，下風口25 m處安置Fluke 923型風速測量儀，對爆破現場當時風速進行測量。同時，為便于更近距離、更完整地拍攝，在風速測量儀上方10 m處架設EOS 70D相機，設置相機模式為高頻，對粉塵擴散全過程進行記錄。粉塵濃度采用FCC-25型防爆粉塵采樣儀進行測試，設置采樣時間為30 min，采樣空氣流量為20 L/min，每2 min采集樣本一次。三臺儀器按線性布置，從爆區下風口20 m處開始，每隔5 m布設一臺，現場儀器布置具體見圖1。

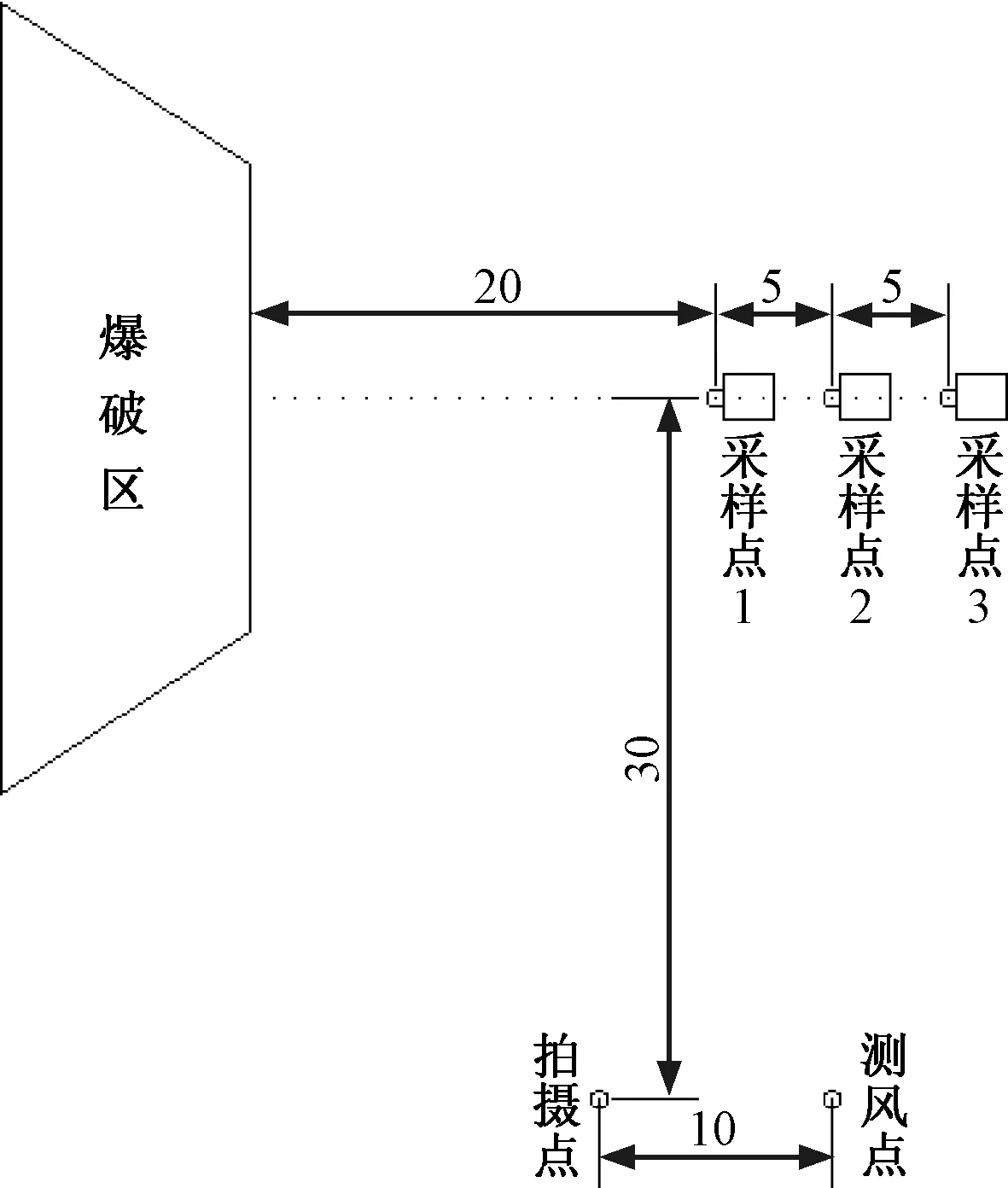
圖1 現場儀器布置示意(單位：m)

1.3.2 試驗結果分析

通過逐幀分析數碼相機記錄的爆破試驗全過程，將露天深孔巖石爆破的粉塵擴散根據粉塵形狀、持續時間、擴散速度等特征分為三個階段：啟蒙階段、舒展階段、擴展階段。同時，將采集的粉塵樣本稱重并數據處理后，得到粉塵濃度隨時間的變化，見表1。

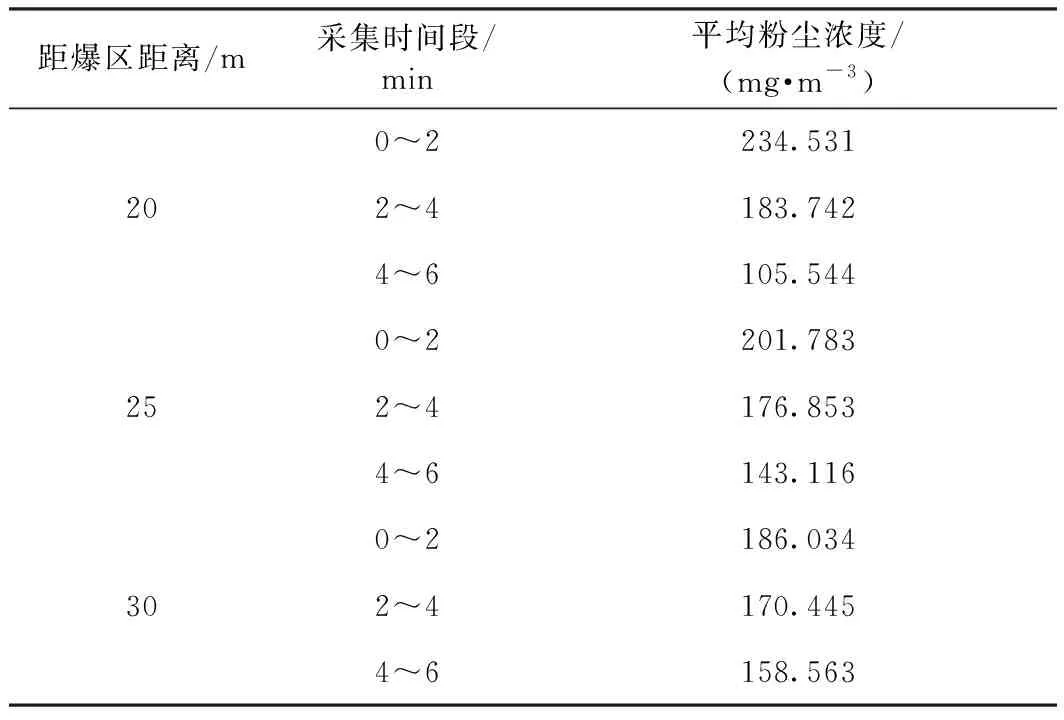
表1 粉塵濃度隨時間變化

從表1中可以看出：①粉塵濃度最大值出現在爆破近期，隨著時間的推移，粉塵濃度逐漸降低，且距離爆區越近，粉塵濃度的下降速率越快。②由于爆破粉塵主要在爆區內產生，同一時刻，距離爆區越近粉塵濃度越高。③粉塵擴散主要受爆破產生的高溫高壓氣體膨脹所致，距離爆區越遠，爆破氣體與溫度壓力以及大氣壓力更易形成平衡，粉塵擴散速率減慢。

1.3.3 計算結果分析

2021年5月22日16時，在北京郊區進行爆破試驗，當時天空晴朗，風速為1 m/s，爆區長度為40 m、寬度為13.5 m，一次爆破總藥量為5.04 t，依據式(8)、式(9)計算得出：Q=716.56 kg、W=142.17 kg/t

同時，根據粉塵排放量，利用式(6)，計算得出不同距離的粉塵濃度關系，見圖2。

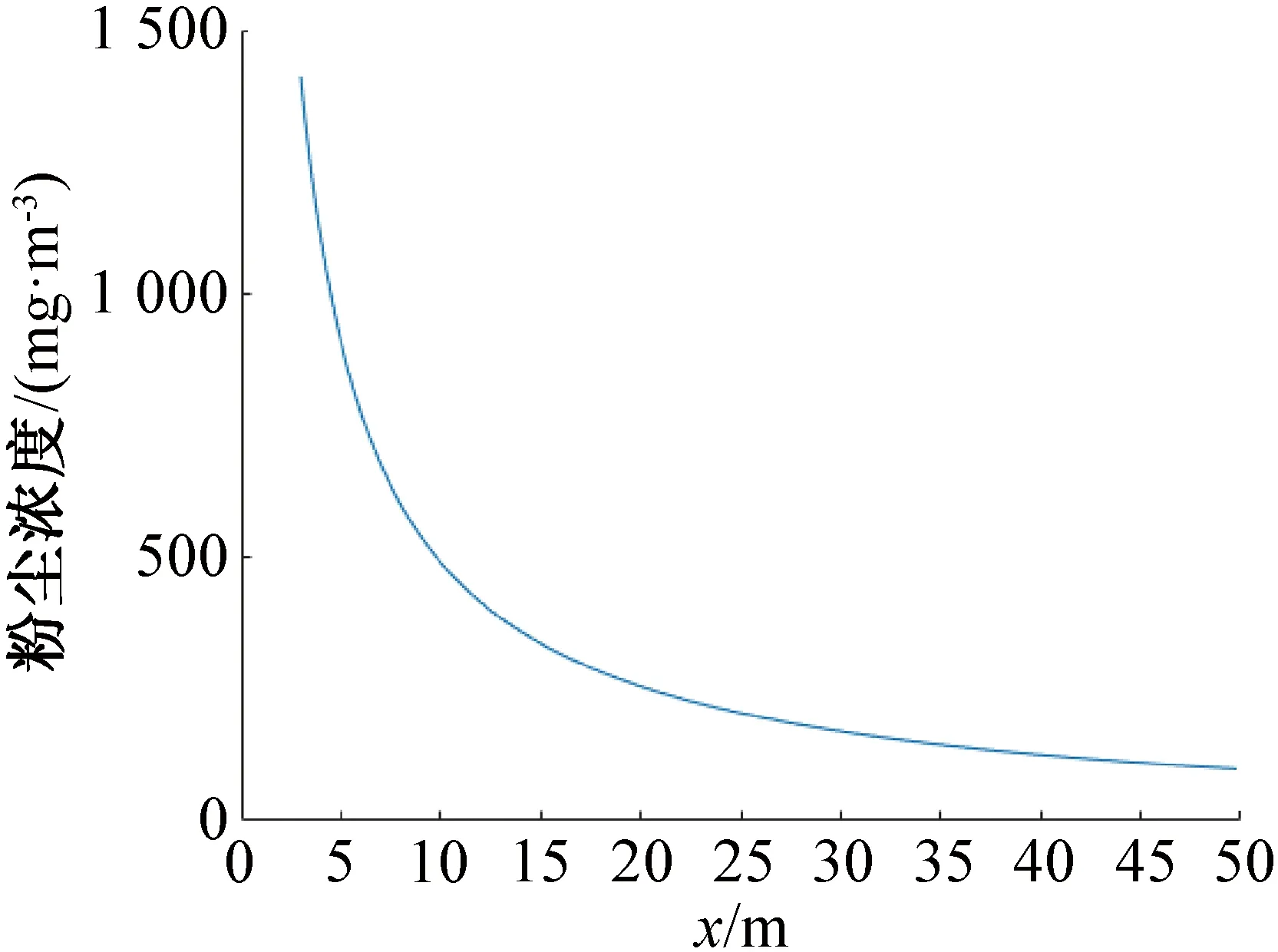
圖2 粉塵濃度隨x方向的變化規律

由圖2分析可得，粉塵濃度q隨著距離x增大而減小，當x<30 m時粉塵濃度大且急劇下降，當x>30 m粉塵濃度趨于緩和，因此水袋應在爆破區域外30 m范圍內鋪設效果最佳。

依據式(5)，將爆破區域寬度y考慮進去，得到z=0時，粉塵濃度q隨x、y的變化，見圖3。

圖3 粉塵濃度隨x、y方向距離的變化規律

從圖3中分析得出，粉塵濃度q隨著爆心距離y增大而減小，且基本符合對稱分布。當y<20 m時粉塵濃度大且急劇下降，當y>20 m粉塵濃度小也趨于緩和。可以看出爆破粉塵濃度最大值出現在爆心處，而爆破區域邊緣的粉塵濃度已經很小，因此設計水袋長度以不大于爆破區域寬度為宜。

利用式(3)對不同高度z的粉塵濃度分布規律進行計算，如圖4所示。

圖4 粉塵濃度隨x、y、z三向距離的變化規律

從圖4中分析得出，粉塵濃度q隨著高度z的增大而減小，當z<2 m時粉塵濃度由爆生氣體所攜帶粉塵量決定，當z>2 m粉塵濃度主要受大氣擴散因素影響，爆破近區粉塵濃度逐漸小于爆破中遠區，當z>13 m粉塵濃度趨于零。因此，水袋炸高設計時，只要水霧高度大于13 m，就可以實現水霧對爆炸產生粉塵的全覆蓋。

2 數值模擬及結果分析

根據現場露天臺階爆破試驗模型的布置和尺寸，使用Soildworks建立三維幾何模型，如圖5所示。其中，臺階傾角為75°，梯段高度為12 m，底盤抵抗線為3.8 m，炮孔間距為4.5 m，炮孔排距為3.8 m，炮孔孔深13.5 m，超深1.5 m。

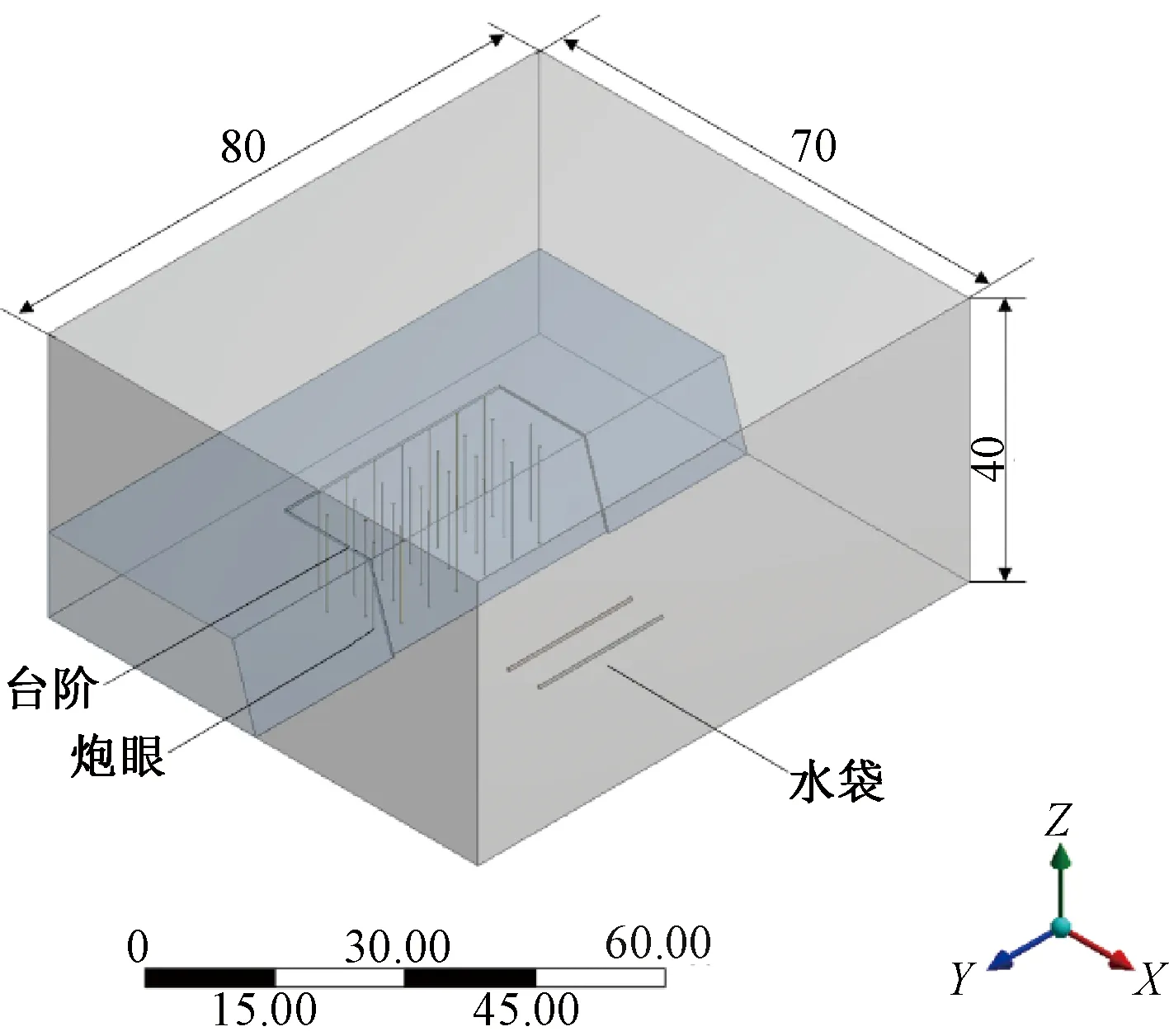
圖5 路塹爆破三維幾何模型(單位：m)

邊界條件和求解過程相關參數見表2。

表2 邊界條件及求解參數設置

為了分析爆破粉塵濃度隨時間的變化規律，在數值模擬過程中設置監測點和線，以分析不同位置處粉塵濃度隨時間的變化規律，如圖6所示。

圖6 監測點和監測線位置圖(單位：m)

其中沿著x方向等間距共設置7個監測點：1(5 m,5 m,0)，2(10 m,5 m,0)，…，7(35 m,5 m,0)，深孔爆破監測點粉塵濃度隨時間變化如圖7所示。對露天臺階附近的濃度時空分布特征進行分析，以點2為基點，分別在x，y，z方向設置line1、line2、line3三條監測線，如圖8所示。

圖7 監測點粉塵濃度隨時間的變化過程

沿監測點的x軸方向，各點粉塵濃度隨著時間的推移，總體呈先急劇上升至峰值，后緩慢下降的分布趨勢，監測點離深孔爆破區域的距離越遠，粉塵濃度峰值越低且達到峰值所需的時間越晚。如圖7所示，點1～7分別在55、55、55、70、60、70、60 s時粉塵濃度到達峰值0.031 2、0.015 1、0.012 6、0.009 2、0.004 9、0.002 8、0.001 5 kg/m3。同時，可以看出點6 由于位于30 m以外粉塵濃度基本保持不變且數值微小。

由圖8可知：

(1)沿監測線line1，如圖8(a)所示，在臺階起爆瞬間粉塵濃度達到最大，并隨著距離的增加整體呈逐步降低的分布趨勢；而對于同一檢測點，隨著時間推移，其粉塵濃度先增大后逐步下降。

(2)沿監測線line2方向，如圖8(b)所示，由于監測線與露天臺階爆破區域存在一定距離，故隨著時間的推移，粉塵濃度在z軸方向整體呈現先上升后減少的變化規律，且在爆破后30～60 s內達到峰值；在監測點z=0兩側等間距的其他監測點，隨著時間和距離的增加呈現大致對稱分布的態勢；當大于爆區寬度時，粉塵濃度已降至最大粉塵濃度的25%以下。

(3)沿監測線line3方向，如圖8(c)所示，不同時刻下的粉塵濃度均隨著高度的增加呈現先增大后減小的趨勢，這是由于爆破過程中的粉塵沿著垂直爆破面方向擴散；在高度小于2.5 m時，粉塵呈現逐步上升至峰值的趨勢；隨著高度的持續上升，絕大多數的粉塵顆粒難以繼續克服重力作用繼續向上擴散，故呈下降的趨勢，并在13.75 m附近基本趨于穩定。

圖8 監測線粉塵濃度隨時間的變化過程

3 實例驗證

3.1 試驗概況

試驗選擇在海南昌江石灰巖礦區進行，巖石硬度適中。首先，在爆區拋擲方向布設兩排水袋，水袋與自由面的距離按不超過30 m布設，分別設為15、25 m；水袋長度按爆區一半寬度30 m布設；每個水袋炸高按15 m左右控制，使用3根導爆索引爆，起爆時間分別滯后第一排孔1、1.5 s起爆。其次，在自由面前方80 m處布設兩臺測塵儀。最后，在距自由面50、100、150 m處布置集塵盒檢測單位面積落塵量。現場試驗布置和效果見圖9、圖10。

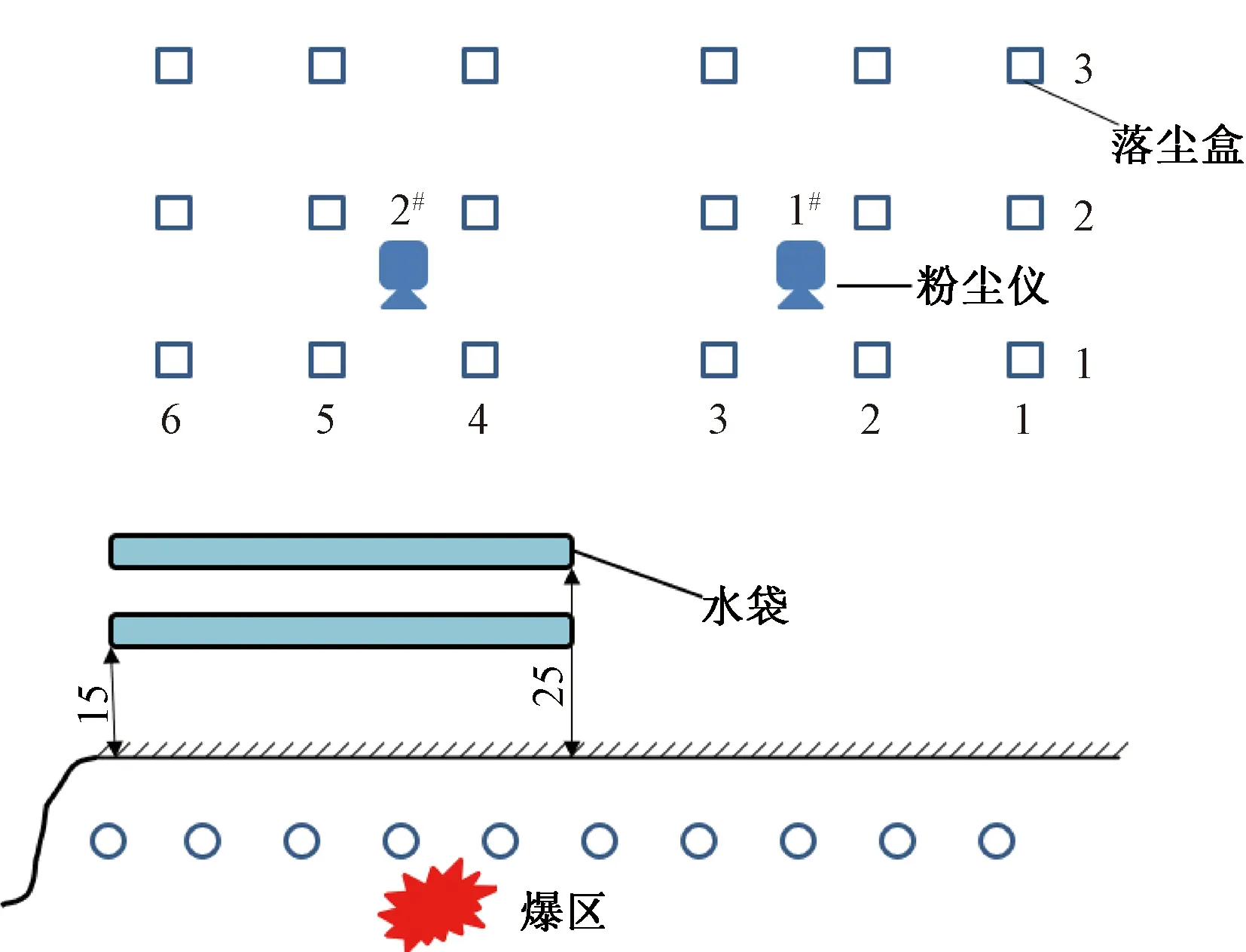
圖9 試驗方案示意圖(單位：m)

圖10 粉塵和爆炸水霧的作用過程

3.2 試驗結果及分析

通過圖10可以看出，在有水袋布設的方位，由于采用了水霧捕獲粉塵的措施，爆破粉塵濃度明顯小于沒有采用任何降塵措施的一側。

對落塵盒和測塵儀采集的結果進行數據處理分析，見表3、表4。

表3 落塵量統計值

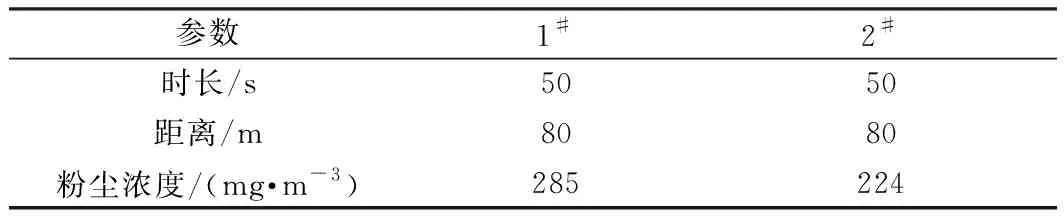
表4 不同措施下粉塵濃度

從表3可以看出，在采用水霧降塵措施和未采用降塵措施后方50、100、150 m處，粉塵量分別增加31%、增加22%和減少27%。說明有水霧的情況下，水霧捕獲塵粒作用明顯，加速了塵粒的沉降，在近區大部分粉塵就已降落，遠區受爆破產塵總量影響落塵量減小。

從表4數據分析可知，爆后50 s，在采用水霧降塵措施后方粉塵濃度比未采用降塵措施減少了27.2%，降塵效果明顯。

4 結論

在研究爆破產塵理論的基礎上，本文將高斯擴散模型引入到爆破粉塵擴散規律認識中，利用Matlab和Ansys Fluent軟件對粉塵擴散進行了數值模擬，并用實例進行測試和驗證，得出以下結論：

(1)基于高斯擴散模型，計算得出此次爆破產塵總量為716.56 kg，爆破粉塵排放強度為142.17 kg/t。

(2)基本認清爆破粉塵擴散規律：①從下風方向看，粉塵濃度隨著距離增大而減小，當粉塵距離自由面30 m以遠后，粉塵濃度變化趨于緩和且數值很小；②從爆區寬度看，粉塵濃度隨著距爆區中心距離增加而呈現大致對稱分布的態勢，當大于爆區寬度時，粉塵濃度已降至最大粉塵濃度的25%以下；③從爆破粉塵高度看，粉塵濃度均隨著高度的增加呈現先增大后減小的趨勢，隨著高度上升至13.5 m左右，粉塵濃度基本趨于穩定且微小。

(3)自由面前水袋設置參數基本確定，水袋設置距離自由面不超過30 m，水袋長度不超過爆區寬度，水袋炸高13.5 m為益。

(4)最后通過實例驗證了基于以上參數設置，爆破水霧降塵技術的可行性和有效性，降塵效果達到27.2%。

本方法從粉塵擴散模糊性和隨機性的角度出發，客觀科學地模擬計算了粉塵擴散規律和擴散范圍，為現場采用水霧降塵施工提供了可復制、可推廣的方法。