基于修正KMV-GARCH模型的我國中小企業信貸風險研究

宋軼

【摘? 要】在中小企業普遍面臨融資難的國內背景下，正確測度中小企業信貸風險不僅有利于解決中小企業融資難、融資貴的問題，而且在進一步煥發國內市場經濟活力方面也發揮著十分重要的作用。通過修正KMV-GARCH模型，使其更符合我國中小企業發展現狀，可以發現以違約距離DD為主要衡量標準可有效評估我國中小企業的信貸風險。通過實證，論文得出：一般情況下，違約距離越大，中小企業的信貸風險越小;股票年收益波動率越大，違約距離普遍越小。

【Abstract】In the domestic context of small and medium-sized enterprises generally facing financing difficulties， the correct measurement of credit risks of small and medium-sized enterprises is not only conducive to solving the problem of difficult and expensive financing of small and medium-sized enterprises， but also plays a very important role in further invigorating the domestic market economy. Through the modified KMV-GARCH model， which is more in line with the development status of small and medium-sized enterprises in China， it can be found that the default distance DD as the main measurement standard can effectively evaluate the credit risk of small and medium-sized enterprises in China. Through the empirical research， the paper concludes that： in general， the larger the default distance， the smaller the credit risk of small and medium-sized enterprises; the greater the volatility of stock annual returns， the smaller the default distance is generally.

【關鍵詞】KMV模型;中小企業;信貸風險

【Keywords】KMV model; small and medium-sized enterprises; credit risk

【中圖分類號】F276.3;F832.4? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文獻標志碼】A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?【文章編號】1673-1069（2022）01-0143-04

1 引言

我國中小企業信貸風險較高，普遍存在融資難問題，盡管近年來我國相關部門及地方各級政府均出臺了支持中小企業融資的文件政策，但由于制度流程和監管程序等方面尚存在可完善之處，所以當下我國中小企業融資情況雖有改善，卻仍未達到政策出臺時所期望達到的理想效果。本文希望通過研究對中小企業信貸風險的度量方法，利用合理的模型更加準確地量化中小企業的信貸風險，并為銀行等金融機構提供參考，從而推動解決我國中小企業融資難的問題，進一步激發市場活力，并有效保護商業銀行自身的信貸資金安全。

2 中小企業信貸風險及KMV模型概述

2.1 中小企業信貸風險分析

中小企業是指在人員配置、企業經營等方面規模相對較小的企業。由于中小企業資產規模較小，作為貸款條件的抵押資產普遍不足，融資渠道較窄，使得其融資效果無法達到預期。同時中小企業本身存在的經營風險和信用風險導致商業銀行在為其提供貸款前，會更謹慎地對其進行審查評估，因此銀行需要一套較科學實用的信貸風險評估體系來對中小企業進行貸前審查，從而在盡可能保證資金安全的前提下實現收益最大化。然而當下國內信貸體系建設仍不完善，尤其中小企業普遍存在信用信息缺失等問題，這種信息不對稱增加了商業銀行為中小企業提供貸款的成本和風險，因此有必要引入實用性和準確性更強的模型對中小企業信貸風險進行度量。

2.2 KMV模型實證原理概述

KMV模型認為企業股權價值可被看作看漲期權，債務到期日如果企業資產價值高于債務值（即達到模型中的違約點），那么企業股權價值等于資產與債務值之間的差額，如果企業資產價值低于債務值，那么償還債務后企業相應股權價值則為零。KMV模型從動態角度量化分析我國上市中小企業的信貸風險，而該模型所計算出的違約距離等指標也可比較直觀地得出我國中小企業的信貸風險程度。

2.3 KMV模型適用性分析

KMV模型基于現代期權定價理論，利用公開財務數據和股票交易數據進行計算，數據可得性較強，彌補了我國中小企業數據體系尚不完善的不足;通過結合實時變化的股票數據，有助于對中小企業信用風險進行動態分析并及時評估重構新形勢下中小企業信用體系評價標準。然而傳統KMV模型在指標參數設置等方面對我國中小企業分析的準確性不足，所以本文引入GARCH模型及最新市場數據來對KMV模型進行修正。

3 KMV模型原理與修正改進

3.1 KMV模型原理與步驟

3.1.1 KMV模型假設前提

①市場無摩擦，即不存在交易成本和稅收。②市場無風險利率可看作固定的常數。③企業資產價值符合正態分布，屬于隨機的布朗運動;股票價格服從對數正態分布。④當企業資產大于負債時，企業不會違約;反之則企業有違約的風險。

3.1.2 KMV模型基本求解步驟

非流通股不能像流通股一樣在二級市場上自由流通，而有研究發現每股凈資產對協議轉讓價格的影響最顯著，所以股權市場價值和債務價值可分別通過以下公式計算：

股權市場價值VE=流通股市值+（0.995 76+0.609 73×每股凈資產）×非流通股股數? ? ? ? ? ? ? ? ? ? （1）

債務價值VD=流動負債+長期負債? ? ? ? ? （2）

根據假設3，股票價格服從對數正態分布，所以股票日收益率Rt的計算公式為：

Rt=ln（）? ? ? ? ? ? ? ? ? （3）

其中，Pt為當天股票收盤價格，Pt-1為上一天股票收盤價格。

股票價格年收益波動率的傳統方法是先計算一段特定時期中股票日收益率標準差，然后通過日收益波動率推算相應的股票年收益波動率，用公式可以表示為：

股票日收益波動率σ=? ? ? （4）

股票價格年收益波動率σE' =σ? ? ? ? ? ? ? （5）

其中，N表示一年中股票的實際交易天數（不包括公休日、節假日和停牌日）。

根據Black-Scholes-Merton期權定價模型，可對應求出上市企業的資產價值波動率和企業的資產價值：

VE=VAN（d1）-e-rTVDN（d2）

σE=

×N（d1）×σA? ? ? ? （6）

其中，N（d）=edx，d1=，d2=d1-σA，VE為股權市場價值，VD為債務價值，r為無風險利率，T為債務到期時間，σE為股票年收益波動率。

根據KMV模型歷史計算經驗，違約點DP的值可以用以下公式表示，該違約點被認為是企業發生違約行為可能性最大的點：

DP=STD+LTD? ? ? ? ? ? ? ?（7）

其中，STD表示企業的短期債務，LTD表示企業的長期債務。

結合以上結果，違約距離DD的計算公式如下：

DD=? ? ? ? ? ? ? ? ? （8）

根據KMV模型假設3，企業的資產價值服從正態分布，所以相應預期違約概率EDF的計算公式為：

EDF=P（）=N（-DD）=1-N（DD）? ? ? （9）

最終本文的理論依據為違約距離越大，預期違約概率越低，即相應上市中小企業的信貸風險越低。

3.2 引入GARCH模型及最新市場數據對KMV模型進行修正

3.2.1 對股票價格年收益波動率σE的改進

考慮到股市具有波動聚集性，且股票收益波動率不斷變化，所以在后續分析中不能簡單以歷史數據代替未來數據。為了應對時間序列出現異方差，本文運用GARCH（1，1）模型對各上市中小企業的股票價格年收益波動率進一步修正。

以下是GARCH（1，1）模型關于均值和方差的一般表達式，每家上市中小企業修正后的股票年收益波動率都可以用該模型求出：

Rt=c+μt，μt～（0，σ）? ? ? ? ? ? ? （10）

σ=α0+α1 μ+βσ? ? ? ? ? ?（11）

忽略協方差影響，股票價格年收益波動率的平方可以表示為每日方差的累加：

σ=∑σ=σ+σ+…+σ? ? ? ? ? ?（12）

整理上述公式，可得最終股票價格年收益波動率的計算公式：

σE=? ? ? ? ? ? ? ? （13）

3.2.2 對違約點DP的改進

傳統KMV模型在計算上市公司違約點時，參數設定為短期債務前系數為1，長期債務前系數為0.5，這是基于美國企業數據所求出的一般性經驗公式，但考慮到國內市場與美國市場存在一定程度的差異，且中小企業在經營規模和違約可能性等方面存在特殊性，所以本文結合我國行業內若干家中小企業數據，以企業總資產為被解釋變量，企業短期債務和長期債務為解釋變量，在剔除30個樣本中3家無長期債務的特殊樣本后進行最小二乘回歸，從而對違約點的公式參數進行修正。

將STD變量前的系數標準化為1，可以得到標準化后的違約點DP的計算公式為：

DP=STD+1.317 8LTD? ? ? ? ? ?（14）

經檢驗，違約點公式中的兩系數分別在10%和5%的顯著性水平下成立，盡管R2=0.407 164，但F統計量的相伴概率為0.000 721，小于0.01，所以仍可認為該回歸模型總體回歸效果顯著。

4 基于修正KMV-GARCH模型我國中小企業信貸風險實證研究

4.1 樣本數據選取

為了建立在我國適用性更高的國內中小企業信貸風險評價體系，本文選取種植業與林業、半導體及元件、化學制品等10個代表性行業中30家上市中小企業進行研究，其中包括25家正常經營的中小企業和5家被ST的中小企業（其中樂通股份于2021年3月23日成功摘帽，由*ST樂通變更為樂通股份，但本文分析數據的基準年為2019年，所以暫將其歸類為被ST的企業）。

鑒于近年來中國經濟發展迅速，國內各行業的營業收入均在不同程度上受到通貨膨脹等因素影響而逐年上漲，但《中小企業劃型標準規定》發布于2011年且至今仍未更新，所以本文結合當下市場實際情況，從同花順與Wind數據庫中提取相關數據，將選取中小企業的標準設定為：①在中小企業板上市;②營業收入在50 000萬元以下。

4.2 參數設定

①計算股權市場價值時，本文采用當年12月各交易日收盤價平均數作為流通股價格。②計算股票年收益波動率時，本文選取各上市中小企業在2019年1月2日至2019年12月31日期間各交易日的收盤價數據作為樣本進行計算，2019年股市交易日共計244天。③本文選擇中國人民銀行在2019年的一年期整存整取定期存款利率作為市場的無風險利率r，即r=1.50%。④本文研究的基準期間為1年，所以T=1。

4.3 實證結果分析

4.3.1 違約距離DD

基于修正KMV-GARCH模型，本文計算出30家來自不同行業的上市中小企業樣本違約距離，如表1和表2所示。

本文發現我國上市中小企業的違約距離大部分落在（1，3），中小企業之間存在一定的差距，寶鼎科技的違約距離最小，為1.292 3，而華東數控的違約距離達到了3.147 7。

一般認為，違約距離越大，企業違約的概率越低，通過對30家中小企業違約距離進行描述性統計分析，可初步得出相比違約風險普遍更高的被ST的中小企業，正常經營的中小企業的平均違約距離更大，發生違約的可能性更低，此結果也符合市場的普遍認知規律。

然而這一結論并不絕對，以樂通股份為例，其近年來積極開展新型業務并不斷優化資產配置，2020年企業已實現凈利潤730.98萬元，扭虧為盈，這可以部分解釋近期樂通股份成功摘帽的原因。而計算得到的樂通股份違約距離大于ST組均值同時小于正常組均值，也可說明即使在未摘帽前，盡管樂通股份的信貸風險與正常經營的中小企業相比仍相對較大，但也已在一定程度上優于一般的被ST的中小企業。

因此，銀行在對中小企業放貸時，不能將中小企業的信貸風險簡單以企業是否被ST劃分，而要結合中小企業的實際情況具體分析，從而在保證銀行信貸安全的基礎上合理有效地為中小企業提供融資支持，最大程度激發金融市場的活力。

4.3.2 違約距離DD與股票年收益波動率相關性分析

本文借助SPSS軟件對上市中小企業樣本的違約距離與相應股票價格年收益波動率進行Pearson相關性分析，得出兩個指標間相關系數為-0.968，從而說明我國上市中小企業的違約距離與其股票價格年收益波動率之間呈極強負相關關系。

股票價格年收益波動率這一指標對分析我國上市中小企業信貸風險具有很強的參考性，一家上市中小企業的股票價格年收益波動率越大，其違約距離一般越小，預期違約概率一般越大，相應上市中小企業發生違約的可能性就會越大。

4.4 實證結果檢驗

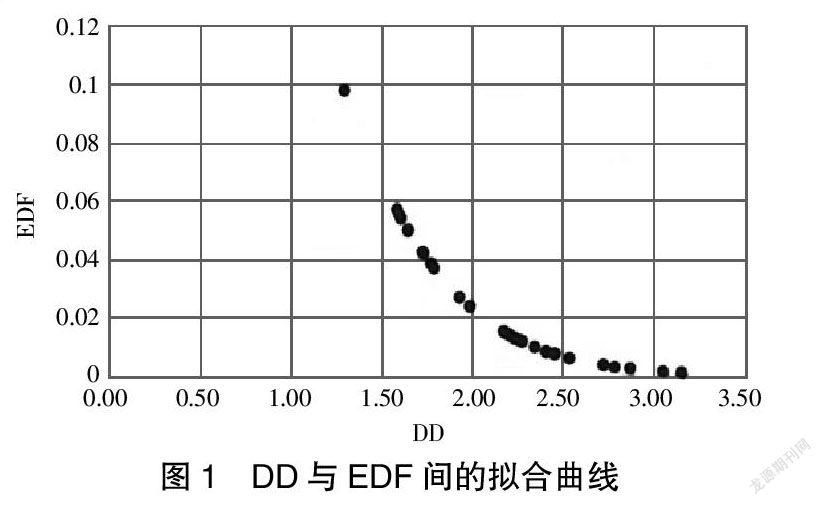
4.4.1 違約距離DD與預期違約概率EDF間的擬合曲線

為了檢驗所構建的模型對度量我國上市中小企業信貸風險的合理性，本文擬合出所計算的違約距離與預期違約概率之間的關系，如圖1所示。

可以看出，違約距離與預期違約概率之間呈現出明顯反向變動關系，即違約距離越大時，預期違約概率越小，即相應上市中小企業的信貸風險越小，反之同理。

這一結論符合兩變量之間的初設關系，所設模型擬合效果較好。但是尤其當違約距離大于3時，預期違約概率已十分接近于0，此時使用預期違約概率對上市中小企業的信貸風險進行量化評估不夠有區分度，因此在這種情況下，本文傾向于使用違約距離來判定我國上市中小企業的信貸風險。

4.4.2 ROC曲線檢驗

根據上述計算結果，利用SPSS軟件繪制ROC曲線，結果如圖2所示。計算結果表明，依據修正KMV-GARCH模型所計算出的違約距離對我國上市中小企業信貸風險的評估準確性為74.4%，因此認為本文所建立模型的判定能力較好。

5 結論與建議

5.1 結論

第一，一般情況下，違約距離DD越大，通常可以認為相應上市中小企業的信貸風險越小，但在實際工作中，不僅要參考KMV-GARCH模型所計算出的理論結果，同時也要結合上市中小企業的實際情況，從而綜合作出決策，合理安排貸款。第二，中小企業的違約距離DD與其股票價格年收益波動率之間呈現極強的負相關關系，所以在實際工作中不僅可以利用違約距離來判斷上市中小企業的信貸風險，也可以通過企業的股票價格年收益率波動率來進行輔助分析，在大多數情況下，股票價格年收益波動率越大，相應上市中小企業的信貸風險往往越大。第三，使用改進KMV-GARCH模型對我國上市中小企業的信貸風險進行分析時，獲取數據比較容易，計算步驟較為清晰，且基于真實數據所計算出的違約距離DD和預期違約概率EDF可以較為直觀地反映出國內上市中小企業的信貸風險狀況，因此采用KMV-GARCH模型進行建模分析具有一定的可操作性和參考性。但KMV模型在適用范圍方面存在一定的局限性，且計算過程也有可能由于股票市場不夠有效等情況而出現偏差，所以在現實應用中應同時結合實際綜合分析，從而得出更貼合現實的結論。

5.2 對策建議

第一，建設我國中小企業征信體系，不斷完善相關模型。盡管本文模型可較好分析部分中小企業的信貸風險，但對非上市中小企業的信貸風險卻無法測度，因此有必要加快補充有關數據、持續完善我國中小企業征信體系。在此基礎上，KMV等模型也應繼續修正完善，從而為評估中小企業信貸風險奠定更加堅實的理論基礎。第二，加快更新我國各行業中小企業劃型標準。當前中小企業規模不斷擴張，僅依據10年前的文件對中小企業性質進行界定顯然已不再適用，目前需加快更新我國中小企業劃型標準，從而更加準確地對各行業中小企業的信貸風險進行測度和評估。第三，注重中小企業日常內部風險管理。中小企業在追求利潤最大化目標的同時，也要關注自身的風險管理效果，避免為了追求短期利益而帶來不利經營風險，加大自身違約風險。同時中小企業也應更注重專業人員的培養選拔，風險管理部門職員應在熟悉我國相關金融法律法規的同時也充分了解中小企業的具體情況，要能運用專業知識對中小企業進行個性化的風險管理。

【參考文獻】

【1】張紹敏.基于違約距離的財務預警模型[D].北京：北京大學，2007.

【2】周好文，晏富貴，徐守喜.過度關注與股價波動聚集性[J].西安交通大學學報（社會科學版），2015，35（02）：16-21.

【3】李錦.基于KMV模型的我國商業銀行信貸風險度量研究[D].太原：山西財經大學，2016.