二維橢圓零件排樣問題研究

張 闖，高 強，2*，叢玉龍，蔣興文，周 明

（1.沈陽工程學院，遼寧 沈陽 110136；2.沈陽建筑大學 機械工程學院，遼寧 沈陽 110168）

在大型工業產品中，如機床、輪船及飛機常常需要很多的小零件，如螺釘、螺帽、螺栓和活塞等。在零件的生產過程中，第一步是需要依照零件產品尺寸從原材料中截取初級產品。在這道工序中，不同的截取方案具有不同的材料利用率，而原材料的利用率（原材料截取初級產品的總體積與原材料體積之比）直接影響產品的生產成本。在市場上，零件的截面（表面）形狀是多種多樣的，有圓形、矩形等，零件的厚度（高度）尺寸也是大小不一的。在原材料尺寸固定的前提下，截取初級產品后產生的廢料最少是企業的追求。

本文以6 060 mm×2 160 mm板材加工盡可能多的橫徑為60 mm，豎徑為40 mm的正橢圓形產品為例，探討滿足產品數量要求的整體切割方案。

1 外切矩形件直接排樣

二維零件排樣問題是近年來的研究熱點[1]，首先將橢圓簡化為外切矩形，通過緊密切割[2]（無縫隙排列）的方式建立模型，即矩形件排樣優化。將原材料水平放置，以原材料左下角為坐標原點（0，0），以長邊所在直線為x軸，短邊所在直線為y軸，建立平面直角坐標系。但緊密切割存在橫向擺放、豎向擺放兩種情況如圖1所示。

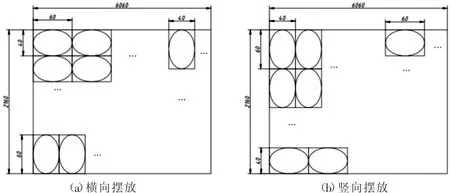
圖1 矩形件排樣

首先若將產品橫向擺放，并且彼此間無縫隙緊密排列。排列到最后可能會出現橫向擺放不足以擺放一塊，但是豎向擺放還有余量的情況。同理豎向擺放會出現橫向擺放不足以擺放一塊，但是橫向擺放還有余量的情況。

對于橫向擺放，先采用從上往下逐排擺列擺放的方式，假設先將t1塊產品緊密橫放排列，t2塊產品緊密豎放排列；再從下往上逐排排列擺放，將t3塊產品緊密豎放排列，t4塊產品緊密橫放排列。n為可切割的產品數，可建立數學模型：

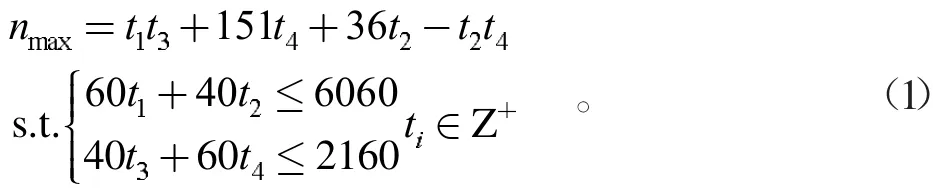
同理，對于豎向擺放，可建立數學模型：

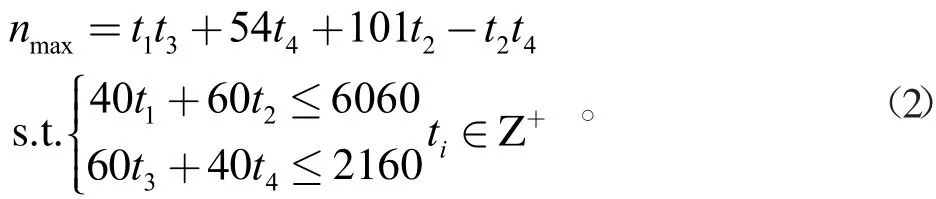
求解后結果見表1，最優結果為5 454塊。

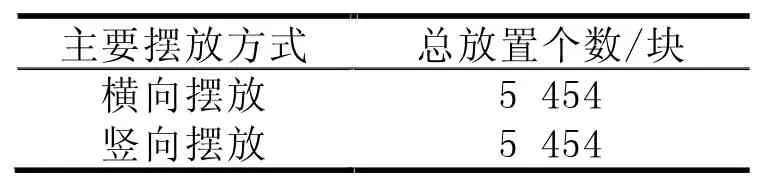
表1 矩形件排樣求解結果

2 外切矩形件優化排樣

由于外切矩形件直接排樣在面對不同規格零件時，需要重新建立數學模型，實用性較差。故將其算法優化[3]，增強算法的實用性。

將第i塊產品中心的坐標與切割方向記為（xi，yi，di），其中i=∈N*，di=±1，（xi，yi）表示第i塊產品的中心坐標，di=1表示第i塊產品的長邊水平切割，di=-1表示第i塊產品短邊的水平切割。為了使原材料的利用率最大，只需總的產品所占面積最大，即可滿足切割產品數目最多。

在約束條件上要確保以下三點：

（1）任意兩塊產品不能重合，即橫坐標或縱坐標滿足式（3）兩種關系之一。

（2）每塊產品必須要在原材料的范圍內，即需要同時滿足式（4）兩種關系。

（3）產品的總面積必須大于等于零，且不能超過原材料面積，即需要滿足式（5）的關系。

綜上，該數學模型可以表示為：

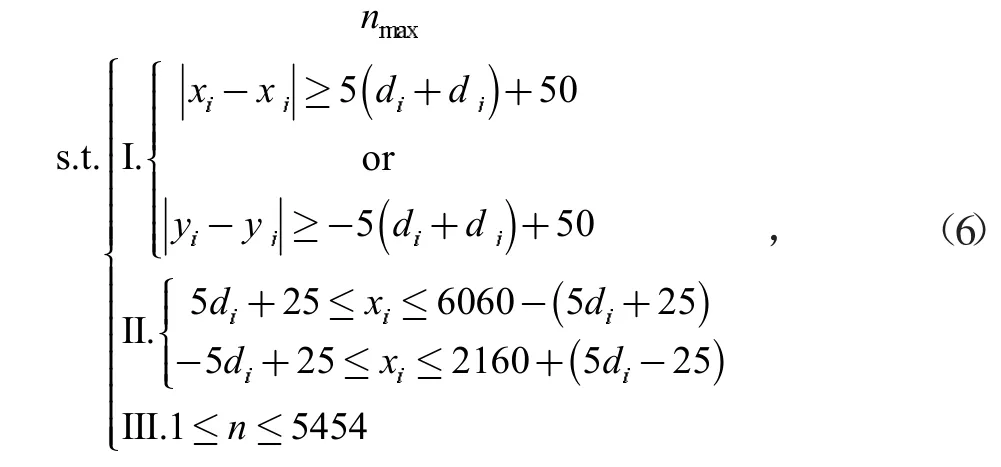
其中：i∈N*，j∈N*，i≠j，n∈N*。

求解結果為最多擺放5 454塊，與外切矩形件直接排樣相同，但建模與計算速度較外切矩形件直接排樣更快，該模型可適用于復雜的矩形切割問題，但對于橢圓切割問題，該方法空間利用率過低，無法滿足設計需求。

3 橢圓最小密排優化

上述模型通過將橢圓簡化為矩形，通過矩形件排樣的算法建立模型，得到了最佳的切割方式，這種模型如果是切割矩形件可以得到最優解，但是切割橢圓由于橢圓面積僅占外接矩形面積的π/4，約為78.5%，顯然不是最優解。而橢圓致密的排列方式一定是要使每一個橢圓盡可能地靠近，并且是按照一定規律排列，如同理想原子的排列一樣。

阿克塞爾圖早在1910年就對圓形的六角密堆積進行了證明[4]，對于圓形而言，六角密堆積是最致密結構，致密度為，其排列方式如圖2所示。

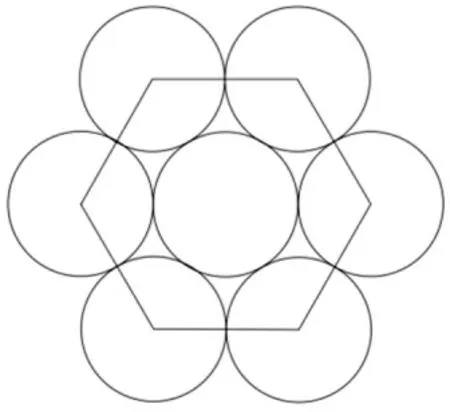
圖2 六角密堆積示意圖

圓的六角密堆積是平面上最有效的堆積方式，所以像橢圓這種的圓錐曲線輪廓的工件，可以根據圓的六角密堆積建立仿射坐標系[5]，將橢圓類比成圓，進行密堆積排列。再對上述算法進行優化，即可得到最優解。

對于橢圓的密堆積排列，首先建立仿射坐標系，該問題不需要建立三維仿射坐標系，在平面內建立二維仿射坐標系即可。即原坐標系內的任意一點（x，y）原本表示為r→=xι→+yJ→，現在仿射坐標系內（x′，y′）的坐標表示為r→=x'ι→+y'J→=xι→+1.5yJ→。通過坐標反變換，即可得到橢圓的密堆積排列如圖3所示。

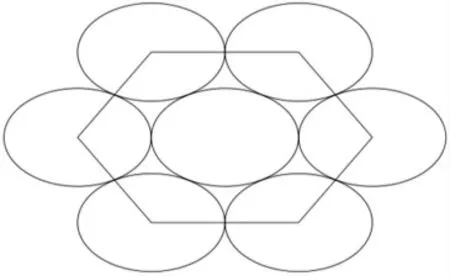
圖3 橢圓件密堆積示意圖

橢圓件的密堆積排列與圓的密堆積排列相似，是有規律的無限排列，若不限制邊界無限排列，其致密度為90.7%。

將第一塊橢圓件貼著原板材左上角排放，則優化后的排列方式求解算法設計思路如下：

Step1：計算奇數行的零件數。

Step2：計算偶數行的零件數。若奇數行剩余長度大于橢圓半長軸，偶數行零件數=奇數行零件數，若不超過a，偶數行零件數=奇數行零件數-1。

Step3：計算出總行數。

Step4：判斷奇數行和偶數行的行數。若總行數為偶數，則奇數行行數=偶數行行數-總行數/2；反之，偶數行行數-（總行數-1）/2，奇數行行數-偶數行行數+1。

Step5：計算出6層的總零件數。

Step6：找出利用率最大的方案。

求解后結果見表2。

表2 橢圓最小密排求解結果

板材橫向擺放的原材料利用率最大，為88.951%，排列數據見表3。

表3 所選方案的詳細結果

4 結束語

二維排樣問題是工業原材料加工中經常遇到的問題，其較強的實用價值引起了國內外學者的廣泛關注。本文根據橢圓零件排樣問題提出了橢圓的密排結構，對零件最優切割方案進行了分析與研究，以期對此項研究工作的開展提供一定參考。