一類偏微分方程在半無窮區域上的空間漸近性質
李遠飛, 肖勝中, 石金誠
(1. 廣州華商學院 數據科學學院, 廣東 廣州 511300; 2. 廣東農工商職業技術學院 科研處, 廣東 廣州 510507)
從數學的角度來研究各種模型時,首先要關心的是這些模型解的全局存在性以及不存在性.在文獻中最常見的是研究模型的解關于時間變量的存在性,文獻[1-2]分別研究了變系數的熱量方程以及高維空間上拋物方程在非線性邊界條件下解的爆破現象,在對已知數據項進行一定假設的情形下,通過巧妙的設置輔助函數,得到了爆破時間的上下界以及全局解存在的條件.文獻[3]考慮了更一般的非線性拋物方程的情形.
本文關注一類來自黏彈性問題的偏微分方程在一個半無窮柱體上的空間存在性和衰減性,這種研究通常被稱為Phragmén-Lindel?f型二擇一研究.與空間衰減性不同,這種研究不需要假設方程的解柱體的無限端方程的解趨近于零這種先驗假設,而是證明方程的解隨距柱體有限端的距離要么指數式增長要么指數式衰減.由于Phragmén-Lindel?f型原理在力學、生物學等學科上的廣泛應用,自20世紀90年代以來逐步取代Saint-Venant原理而成為研究的熱點,出現了大量的成果[4-14].
本文假設Ω表示一個半無窮柱體的內部區域,柱體的有限端記為D位于x1Ox2平面上,柱體的母線平行于x3坐標軸,即
Ω={(x1,x2,x3)|(x1,x2)∈D,x3>0}.
令D(z)表示Ω在x3=z處的截面,即
D(z)={(x1,x2,x3)|(x1,x2)∈D,
x3=z>0}.
本文采取通常所用的符號約定,即用逗號表示求導,重復希臘字母表示從1至2求和,重復英文字母表示從1至3求和,例如:
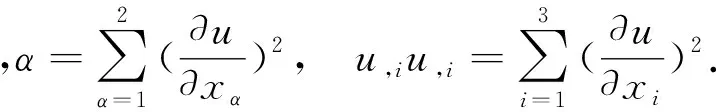
1 準備工作
本文研究以下來自黏彈性問題的偏微分方程[8]:
c(x)utt=[ρ(x,|u|2)u,i],i+γΔut,
inΩ×(0,t),
(1)
u=0, in ?D×{x3>0}×(0,t),
(2)
u=f(x1,x2,t), inD×{x3=0}×(0,t), (3)
u(x,0)=0, inΩ,
(4)
其中?D表示區域D的邊界,△表示三維拉普拉斯算子,表示梯度算子,f是給定的已知函數,x=(x1,x2,x3)以及γ是一個大于零的常數.這類方程也存在于第三類熱傳導的研究中.第三類熱傳導的線性形式滿足我們的假設.注意到,在二維情況下,如果ρ滿足一定的條件時,則方程(1)對應于冪律材料子類的反平面剪切動力學變形[15].
注意到文獻[16]研究了定義在Ω上的二階擬線性方程
[ρ(x,|u|2)u,i],i=f(u),
在柱體的側面上施加了齊次Dirichlet條件和Neumman邊界條件.他們證明了當空間變量趨近于無窮時方程解的空間二擇性.當f(u)=0時,文獻[17-18]分別考慮了非穩態和穩態的情形下在二維區域上解的空間衰減性.本文的主要目的把文獻中取得的結果進一步推廣到模型(1)中來.為此,本文利用加權的能量分析法,在“能量”函數中引入一個待定的大于零的參數,由于此參數是任意的正數,可以得到比上述文獻更快的衰減率.
假設c(x)和ρ分別滿足以下條件:
(a) 0 (5) 現在定義能量函數 (6) 由(5)式可得 (7) 設z0為x3坐標軸上的某一個點.在(6)式中利用散度定理、方程(1)~(4)和(7)式可得 (8) 對(8)式微分可得 (9) (10) χ(z,t)+(0,t). 下一節利用H?lder不等式來推導本文的主要結果,在此過程中沒有使用Schwarz不等式.雖然考慮的是三維的情形,但是事實上本文的分析與空間的維數無關.因此,本文的結果對一維和二維的情形也是成立的. 利用H?lder不等式和算術幾何平均不等式以及條件(a)和(b),可得 |I1|≤ (11) (12) 接下來做以下2種情形分析. (H1) 如果存在z0使得(z0,t)≥0,由于(z,t)≥0,所以(z,t)≥(z0,t)≥0,z≥z0.此時結合(6)式、(11)式和(12)式,可得 (13) 由(13)式可得 z≥z0. (14) 對(14)式從z0到z積分,可得 (z,t)≥(z0,t)edAdτ+ 現定義 (16) 聯合(15)式和條件(a),可得 (17) 其中 對(17)式從z0到z積分,可得 (18) (19) (H2) 如果對任意的z≥0都有(z,t)<0,則結合(6)式、(11)式和(12)式,可得 (20) 由(20)式可得 z≥0. (21) 對(21)式從0到z積分,可得 (z,t)≥(0,t)edAdτ- 由于 所以由(22)式可知當z→∞時-(z,t)指數式衰減于零.聯合(10)式,可得 O(1), (23) 其中O(1)表示當z→∞時的無窮小.把上述分析總結為以下定理. 定理 1設u是方程(1)~(4)的解,其中c(x)和ρ分別滿足條件(a)和(b),則當z→∞時函數(z,t)要么指數式增長要么指數式衰減,即要么(19)式成立要么(23)式成立. 注 1注意到在定理1中獲得的衰減率和增長率與ω相關,而ω是一個任意的常數,所以本文獲得的衰減率和增長率要比文獻中取得指數式衰減率和增長率更快. 注 2由(23)式可知,要使得衰減界有意義,還必須推導-(0,t)的顯式上界. (24) 以及 (25) 記 S(x1,x2,x3,t)=f(x1,x2,t)e-βx3,β>0. 于是由(24)式和方程(1)~(4),可得 B1+B2+B3+B4+B5. (26) 利用Schwarz不等式和算術幾何平均不等式,可得: (27) (28) (29) (31) 取 再把(27)~(31)式代入到(26)式,結合(25)式可得 即 -(0,t)≤C(t), 其中 假設c(x)仍然滿足條件(a),但是條件(b)由以下條件代替 其中K1和K2為大于零的常數.文獻[5,14-15]研究過和(b*)類似的條件.滿足條件(b*)的例子可以寫為 取K1=K2=1,易證上述函數滿足條件(b*). 于是利用條件(b*)計算可得 (32) 把(32)式代入到(11)式可得 |I1|≤ (33) 仍然考慮以下2種情形. (H1) 如果存在z0使得(z0,t)≥0,由于F(z,t)<0,所以(z,t)≥(z0,t)≥0,z≥z0.此時結合(6)式、(12)式和(33)式,可得 (34) 通過與(13)式類似的計算,由(34)式可得 (35) 其中C1是一個大于零的常數. (H2) 如果對任意的z≥0都有(z,t)≤0,則結合(6)式、(12)式和(33)式,可得 -(z,t)=-I1-I2≤ (36) 通過與(20)式類似的計算,由(36)式可得 (37) 其中C2與-(0,t)和dAdτ相關. 把上述分析總結為以下定理. 定理 2設u是方程(1)~(4)的解,其中c(x)和ρ分別滿足條件(a)和條件(b*),則當z→∞時函數(z,t)要么指數式增長要么指數式衰減,即要么(35)式成立要么(37)式成立. 本文研究了方程組(1)~(4)解的空間性質,得到了解的空間增長率和衰減率.解的指數式增長也被稱為解的空間不存在性或空間blow-up.通過設置任意參數ω,證明了增長率和衰減率要比文獻中的結果更快.此外,本文的結果對一維和二維區域上的情形同樣成立.同時,本文仍有更深層次的問題需要研究.一是如果柱體區域被一個錐形區域代替,例如文獻[9-19]分別研究了三維調和方程和二維復調和方程在錐形區域上的空間二擇性;二是在實際狀況中,一個物理現象不可能在柱體的側面上總是滿足齊次Dirichlet條件或Neumann條件.因為由于自然風化、腐蝕或其他原因都會對柱體的側面造成一定的損傷,在這種情況下就需要考慮非齊次邊界條件或者局部非齊次邊界條件,文獻出現了一些相關結果[4,7,11].顯然,這些文獻研究的模型大多比較簡單,把這些結果推廣到方程(1)~(4)甚至更復雜的模型中來是非常有意義的. 致謝廣州華商學院科研團隊項目(2021HSKT01)對本文給予了資助,謹致謝意.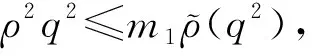
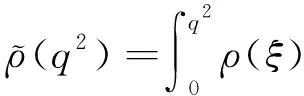




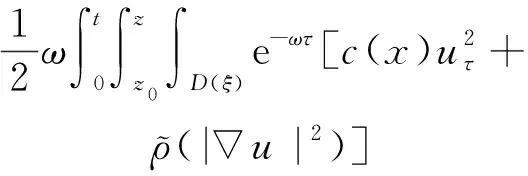

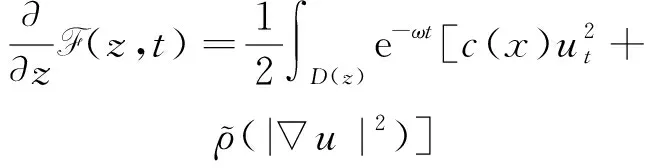
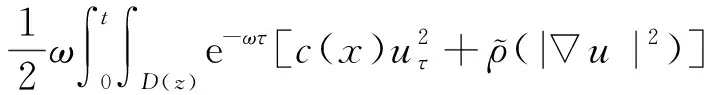

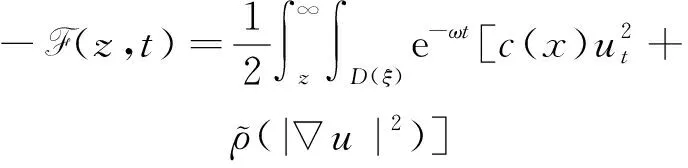


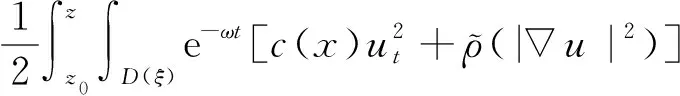
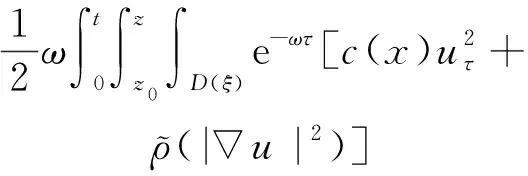

2 空間漸近性質


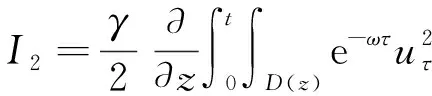
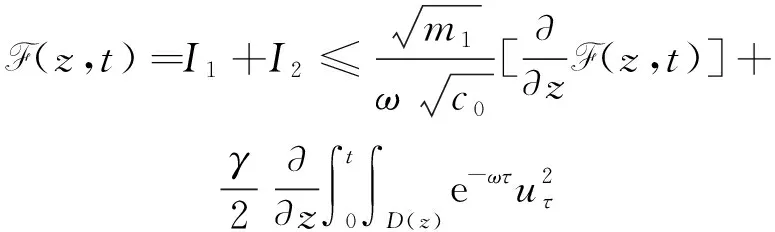
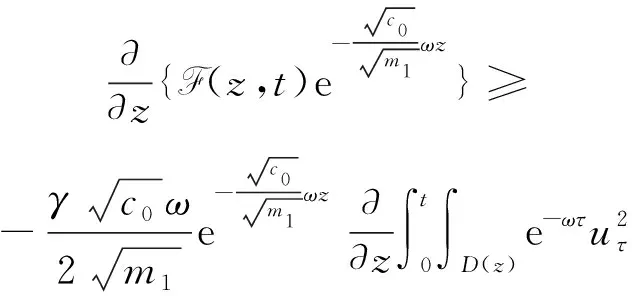


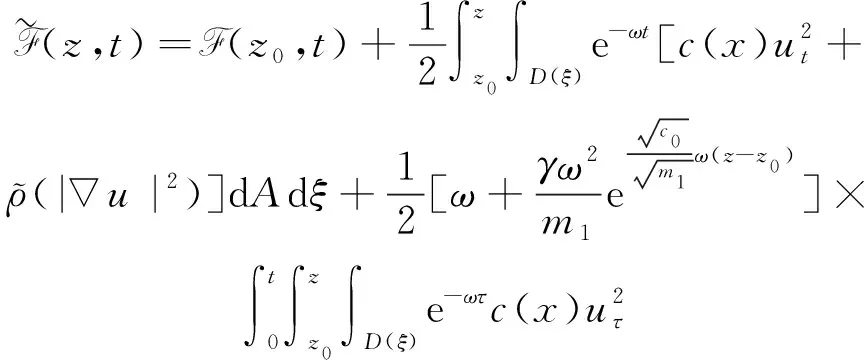


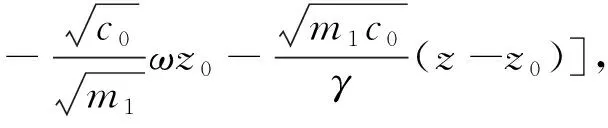

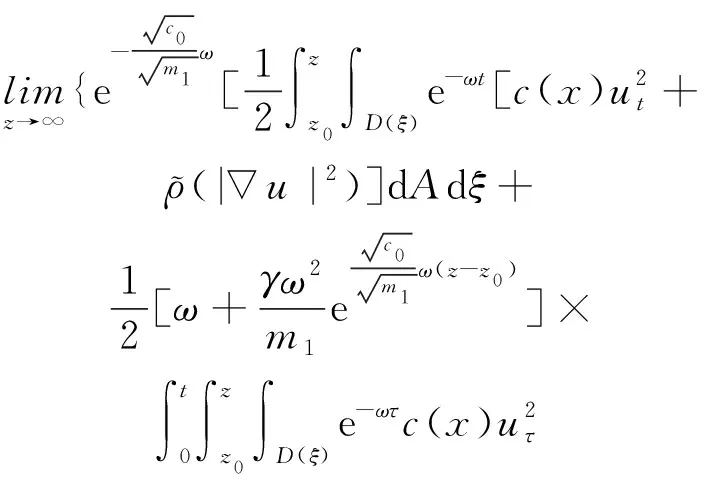



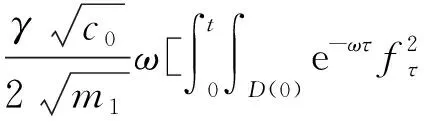
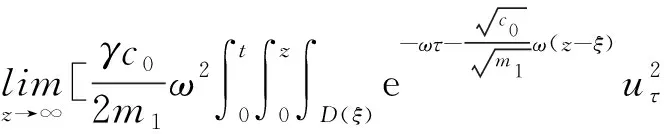


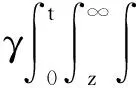
3 全能量估計
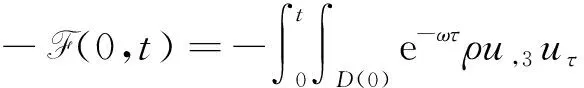
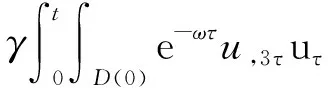
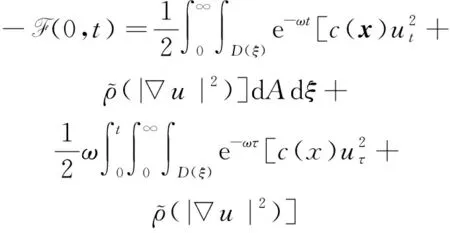







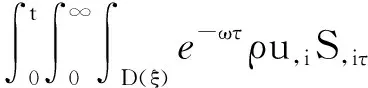


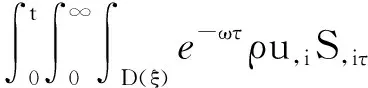



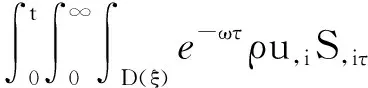


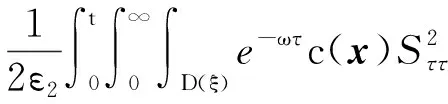
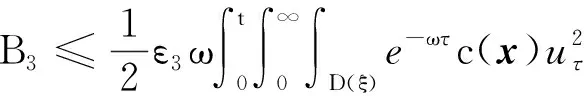




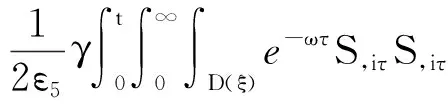
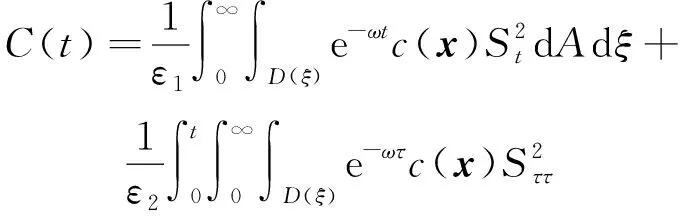
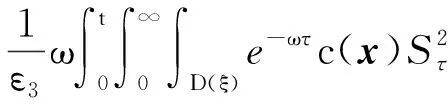

4 新條件下解的空間性質
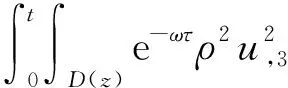



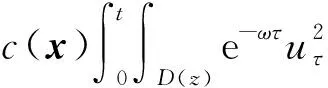



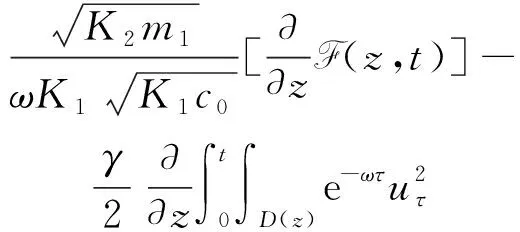



5 結論

