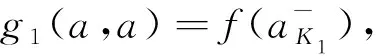單位區(qū)間上由G?del模和Galois聯(lián)絡(luò)生成的三角模

孫 杰, 張德學(xué)

(四川大學(xué) 數(shù)學(xué)學(xué)院, 四川 成都 610064)

三角模在模糊邏輯[1-2]、函數(shù)方程[3]等領(lǐng)域中有很重要的作用,它的結(jié)構(gòu)與構(gòu)造方法得到了廣泛的研究,系統(tǒng)的總結(jié)和論述參見(jiàn)文獻(xiàn)[3-4].利用Galois聯(lián)絡(luò)構(gòu)造三角模是一種很有效的方法,例如連續(xù)的阿基米德模就是由單位區(qū)間上的乘積模和一類特殊的Galois聯(lián)絡(luò)生成的三角模.具體地說(shuō),二元運(yùn)算T:[0,1]2→[0,1]是連續(xù)的阿基米德模當(dāng)且僅當(dāng)存在嚴(yán)格遞增的連續(xù)函數(shù)g:[0,1]→[0,1]使得g(1)=1并且

T(x,y)=g(-1)(g(x)·g(y)),

其中g(shù)(-1)是g的偽逆,即

g(-1)(x)=min{y|x≤g(y)}=

詳見(jiàn)文獻(xiàn)[3]的定理2.2.1.注意到此時(shí)偽逆g(-1)就是g的左伴,文獻(xiàn)[5]指出可以利用Galois聯(lián)絡(luò)構(gòu)造偏序集上的三角模(定義見(jiàn)文獻(xiàn)[6]或定義1.4),并證明了以下結(jié)論.

定理 1.1設(shè)P、Q是有最大元和最小元的偏序集,d:P→Q和g:Q→P是保序映射并且d是g的左伴.若T是P上的三角模且對(duì)任意x,y∈Q恒有

T(g(x),g(y))∈g(Q)∪{ω∈P|ω≤g(0)},

則Tg是Q上的三角模,其中

設(shè)P=Q=[0,1],d┤g:[0,1]→[0,1]是Galois聯(lián)絡(luò),T是[0,1]上的G?del模(也稱取小模),即T(x,y)=min{x,y}.則條件

T(g(x),g(y))∈g(Q)∪{ω∈P|ω≤g(0)}

恒成立,于是由定理1.1得

Tg(x,y)=

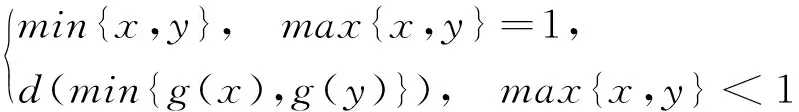
是[0,1]上的三角模,稱為由G?del模和Galois聯(lián)絡(luò)d┤g生成的三角模.本文研究了這類三角模的結(jié)構(gòu),給出了完整的刻畫(huà),證明了兩個(gè)這樣的三角模同構(gòu)當(dāng)且僅當(dāng)彼此的冪等元集之間存在保序同胚.

1 預(yù)備知識(shí)

這一節(jié)簡(jiǎn)要回顧本文將用到的Galois聯(lián)絡(luò)的基本性質(zhì)以及偏序集上三角模的定義.單位區(qū)間上(連續(xù)、左連續(xù))三角模的概念和基本性質(zhì)請(qǐng)參考文獻(xiàn)[3-4].

定義 1.1[7]設(shè)P和Q是偏序集,d:P→Q和g:Q→P是保序映射.若對(duì)任意p∈P,q∈Q都有d(p)≤q?p≤g(q),則稱d是g的左伴,g是d的右伴.此時(shí)稱(d,g)為一對(duì)Galois聯(lián)絡(luò),記作d┤g:Q→P或d┤g.

定理 1.2[7]設(shè)d:P→Q和g:Q→P是偏序集之間的保序映射,則下列條件等價(jià):

1)d┤g;

2)dg≤1Q且1P≤gd;

3) ?x∈P,d(x)=min{y∈Q|x≤g(y)};

4) ?x∈Q,g(y)=max{x∈P|d(x)≤y}.

定理 1.3[7]設(shè)g:P→Q是保序映射并且P是完備格.則g保下確界當(dāng)且僅當(dāng)g有左伴.特別的,保序映射g:[0,1]→[0,1]有左伴等價(jià)于g右連續(xù)且g(1)=1.

定義 1.4[6]設(shè)P是有最大元1的偏序集.稱二元運(yùn)算T:P×P→P是P上的三角模若T在每個(gè)分量上保序且滿足下列條件:

(T1)T(x,y)=T(y,x);

(T2)T(1,x)=T(x,1)=x;

(T3)T(T(x,y),z)=T(x,T(y,z)).

若T是偏序集P上的三角模,則(P,T)是以1為單位元的幺半群.設(shè)T是偏序集P上的三角模,S是偏序集Q上的三角模.稱T與S同構(gòu)若存在序同構(gòu)f:P→Q使得任給x,y∈P,f°T(x,y)=S(f(x),f(y)).

2 主要結(jié)論

除非另外聲明,總是假設(shè)d┤g:[0,1]→[0,1]是Galois聯(lián)絡(luò),Tg表示由G?del模和d┤g生成的三角模,即

Tg(x,y)=

稱單位區(qū)間[0,1]的子集K關(guān)于上確界封閉若任給A?K恒有∨A∈K.特別的,0=∨?∈K.

引理 2.1設(shè)K?[0,1]關(guān)于上確界封閉.任給x∈[0,1],令

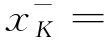
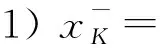
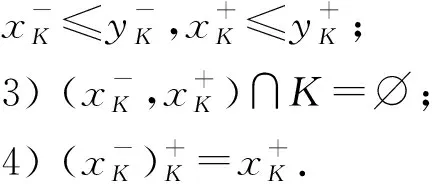
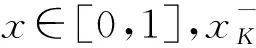
定理 2.2設(shè)K是Tg的冪等元集,即K={x∈[0,1]|Tg(x,x)=x}.則:

1)K={dg(x)|x∈[0,1]}∪{1};

3) 任給x,y∈[0,1),Tg(x,y)=min

證明1) 由Tg的定義,

于是

K={x∈[0,1]|Tg(x,x)=x}=

{x∈[0,1]|dg(x)=x}∪{1}.

(1)

又因?yàn)槿谓ox∈[0,1],dgdg(x)=dg(x),所以K={dg(x)|x∈[0,1]}∪{1}.

2) 為了說(shuō)明K關(guān)于上確界封閉只需證明任給A?K{1},supA∈K.若A=?則supA=0∈K;若A≠?,則由(1)式知對(duì)任意的x∈A都有x=dg(x),于是A=dg(A).因?yàn)?/p>

supA=supdg(A)≤dg(supA)≤supA,

3) 由Tg的定義和2)直接可得.

推論 2.3設(shè)K是Tg的冪等元之集.則下列各條等價(jià):

1)Tg=min;

2)Tg連續(xù);

3)Tg左連續(xù);

4)K=[0,1].

證明只需證明3)?4)?1).

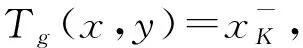
從而K=[0,1].

4)?1) 任給x,y<1,由定理2.2的3)可得

于是Tg=min.

由定理2.2知由G?del模和Galois聯(lián)絡(luò)生成的三角模的冪等元集包含1且關(guān)于上確界封閉,下面的定理表明反過(guò)來(lái)結(jié)論也成立.

定理 2.4設(shè)K是單位區(qū)間[0,1]關(guān)于上確界封閉的子集并且包含1,則存在Galois聯(lián)絡(luò)d┤g:[0,1]→[0,1]使得K是三角模Tg的冪等元集.

由引理2.1的4)可得任給x∈[0,1],g(x)=g(x-).下面說(shuō)明g有左伴,設(shè)為d:[0,1]→[0,1],并且Galois聯(lián)絡(luò)d┤g滿足條件.

第一步g單調(diào)遞增.說(shuō)明g在K上的限制嚴(yán)格遞增.設(shè)x,y∈K且x

第二步g右連續(xù),于是有左伴.任給0≤x<1,分2種情形討論.

情形 1x=x+.由g的定義易知此時(shí)g(x)=x.由x+的定義知存在K中嚴(yán)格遞減的序列{an}n收斂于x.因?yàn)閷?duì)任意n≥1都有

所以{g(an)}n收斂于x(=g(x)).利用g的單調(diào)性以及l(fā)img(an)=g(x)可得g在x處右連續(xù).

情形 2x

第三步K是Tg的冪等元之集,即K={dg(x)|x∈[0,1]}∪{1},其中d是g的左伴.由于K={x-|x∈[0,1]},說(shuō)明任給x∈[0,1],dg(x)=x-即可.

由定理1.2的3),dg(x)=min{t∈[0,1]|g(t)≥g(x)}.一方面,由g(x-)=g(x)可得dg(x)≤x-.另一方面,任給y

定理2.2的3)表明由G?del模和Galois聯(lián)絡(luò)生成的三角模可由它的冪等元集確定,因此這樣的三角模可以通過(guò)它們的冪等元集來(lái)分類,這就是下面的結(jié)論.

定理 2.5設(shè)di┤gi:[0,1]→[0,1]是Galois聯(lián)絡(luò),Ki是三角模Tgi的冪等元之集,i=1,2.則下列各條等價(jià):

1) 三角模Tg1與Tg2同構(gòu),這等價(jià)于存在保序的雙射h:[0,1]→[0,1]使得h°Tg1=Tg2°(h×h);

2) 幺半群([0,1],Tg1)與幺半群([0,1],Tg2)同構(gòu);

3) 存在K1到K2的保序同胚.

證明1)?2) 顯然.

2)?3) 設(shè)f:([0,1],Tg1)→([0,1],Tg2)是幺半群同構(gòu).下面說(shuō)明f在K1上的限制是K1到K2的保序的同胚.

首先,由于f:([0,1],Tg1)→([0,1],Tg2)是幺半群同構(gòu),K1和K2分別是兩個(gè)幺半群的冪等元之集,故f在K1上的限制f|K1是K1到K2的雙射.

其次說(shuō)明f|K1:K1→K2保序.若不然,則存在x,y∈K1滿足xf(y),于是

Tg2(f(x),f(y))≤f(y)

與f同構(gòu)矛盾.

同理可知f|K1的逆映射也連續(xù),于是f|K1:K1→K2是保序同胚映射.

h(x)=