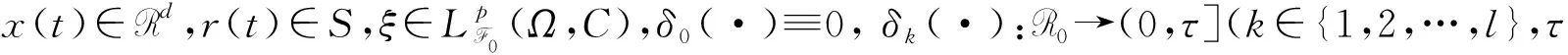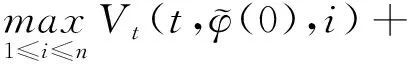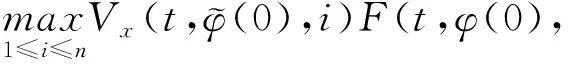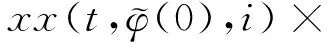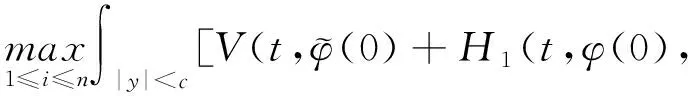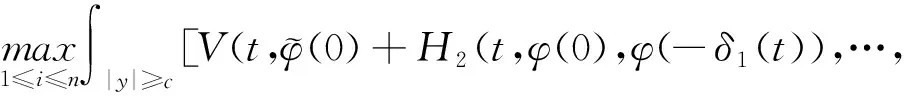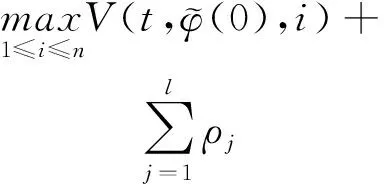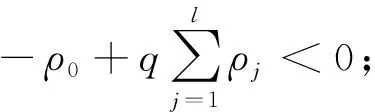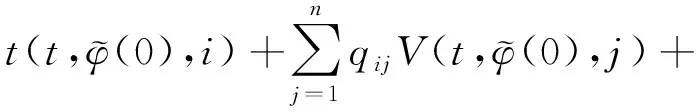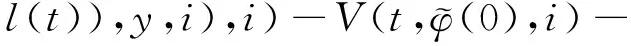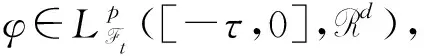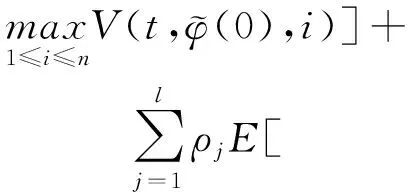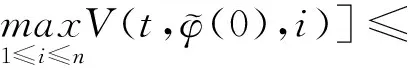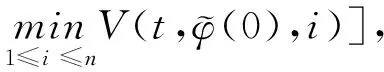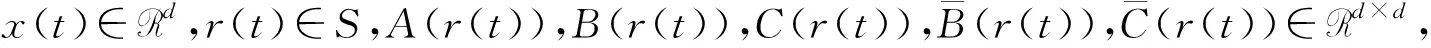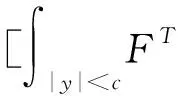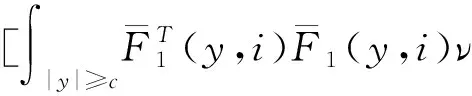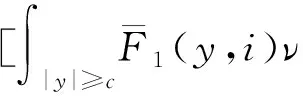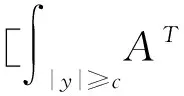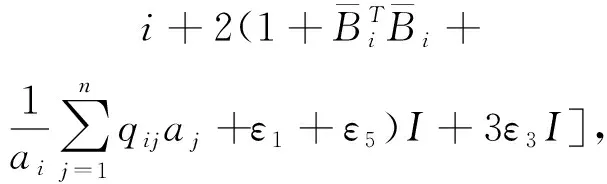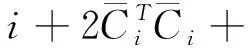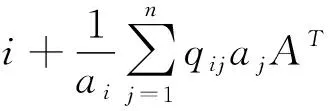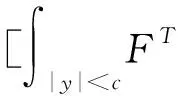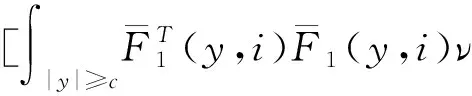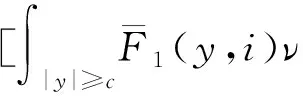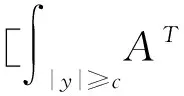具Markov切換和Lévy噪聲的中立型隨機泛函微分方程p階矩指數穩定性
肖 可, 李樹勇
(1. 四川輕化工大學 數學與統計學院, 四川 自貢 643000; 2. 綿陽師范學院, 四川 綿陽 621000)
近幾十年來,由于在自然科學、生物工程、醫學、金融等各個領域的應用,中立型隨機泛函微分方程穩定性被學者們廣泛關注,建立了一系列判別中立型隨機泛函微分方程解穩定性的結果[1-8]. 然而,一個實際的系統常不免有多種隨機因素的介入,Markov切換是一種常見的隨機干擾,由于其樣本路徑的不連續性,Markov切換對隨機微分系統有極大影響,往往會導致系統的不穩定.文獻[6]研究了一類具Markov切換的中立型隨機泛函微分方程解的指數穩定性,利用Razumikhin方法,建立該系統的Razumikhin型穩定性定理,分析了Markov切換對該系統穩定性影響;文獻[7]研究了一類具Markov切換的中立型隨機泛函微分方程解的指數穩定性,通過構造恰當的Lyapunov泛函,并結合隨機分析理論及不等式技巧,建立了該系統解p階矩指數穩定與幾乎處處指數穩定的充分條件,克服了樣本路徑不連續性對穩定性的影響.此外,Brownian運動作為一種連續的隨機過程不能較好地表述那些服從隨機突變的實際系統,而對于隨機突變造成的不連續現象,Lévy噪聲可以更好地刻畫這種隨機突變.因而,具Lévy噪聲的中立型隨機泛函微分方程解的穩定性問題受到學者們重視,文獻[8]研究了一類具Lévy噪聲的中立型隨機泛函微分方程解的穩定性,通過構造恰當的Lyapunov泛函,并結合隨機分析理論與不等式技巧,得到該系統解p階矩漸近穩定與幾乎處處漸近穩定的充分條件.在實際應用中,Markov切換與隨機突變往往同時存在,具Markov切換和Lévy噪聲的隨機泛函微分方程反映了這種現象.但由于樣本軌道不連續,且Markov切換和Lévy噪聲同時存在,穩定性分析面臨更多困難,據我們所知,相關問題研究尚不多見.最近,文獻[9]將Razumikhin方法應用到具Markov切換和Lévy噪聲的隨機泛函微分方程解的穩定性研究上,克服了這一困難,建立了具Markov切換和Lévy噪聲的隨機泛函微分方程解的p階矩指數穩定性判別定理.受此啟發,本文將研究具Markov切換與Lévy噪聲的中立型隨機泛函微分方程解的穩定性,通過使用Razumikhin方法,并結合隨機分析理論以及不等式技巧,建立該系統解p階矩指數穩定的充分條件,進而得到具Markov切換和Lévy噪聲的中立型隨機時滯微分方程解的p階矩指數穩定性判別定理.
1 預備知識
本文|x|表示向量x∈d的歐式范數,w=(w1(t),w2(t)…,wm(t))T(t≥0)是一個m維標準Brownian運動.對非負常數τ,記
τ=[-τ,+∞), CC([-τ,0),d),
C依范數
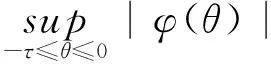
成為一個Banach空間.對每一個C值隨機變量φ(θ,ω),約定
Lpt(Ω,C)={φ:φ是t可測的C值隨機變量,
E‖φ‖p<∞},
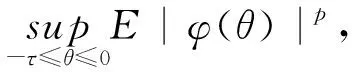
這里E表示關于所給概率測度P的期望.
設{r(t),t≥0}是在完備概率空間(Ω,,P)上的一個右連續Markov鏈,并且取值于有限狀態空間S={1,2,…,n}(n表示正整數),其中生成元Q=(qij)n×n滿足條件:
P{r(t+Δt)=j|r(t)=i}=
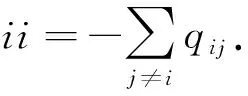
r(t)=r(τk), ?t∈[τk,τk+1),k∈N.
設N是定義在0×(d{0})上的一個泊松隨機測度,是N的補償泊松隨機測度,并且與Brownian運動w(·)相互獨立,這里ν是一個Lévy測度,并且有
考慮如下具Markov切換和Lévy噪聲的中立型隨機泛函微分方程:
d[x(t)-D(t,xt,r(t))]=f(t,xt,r(t))dt+
g(t,xt,r(t))dw(t)+
(1)
其中,x(t)∈d,xtxt(θ)={x(t+θ):-τ≤θ≤0}為一個C值隨機過程,xt-且xt-∈C,函數D:0×C×S→d,f:0×C×S→d,g:0×C×S →d,m和h1,h2:0×C×d×S →d,并滿足后面所需條件,常數c∈(0,+∞]為允許的最大跳躍高度,假定r(t)=i取遍S而不處處注明.
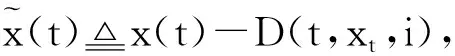
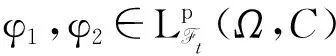
|D(t,φ1,i)-D(t,φ2,i)|≤κ‖φ1-φ2‖.(2)
(A2) 對任意的k=1,2,3,…,存在lk>0使得
|f(t,φ1,i)-f(t,φ2,i)|2∨
lk‖φ1-φ2‖2,
(3)
對任意的t≥0,以及φ1,φ2∈C,且‖φ1‖∨‖φ2‖≤k成立.
(A3) 存在一個常數l >0,使得
對任意的φ∈C以及t≥0成立.
(A4) 對任意的t≥0,有:D(t,0,i)≡0,f(t,0,i)≡0,g(t,0,i)≡0,且對|y| 記方程(1)滿足初值x0=ξ的解為x(t;ξ)(也記為x(t)).顯然,對任意的t≥0,方程(1)有零解x(t)=0. 記C1,2(τ×d×S)為定義在τ×d×S上的所有非負函數V(t,x,i)的集合,并且V對t為一階連續可微的函數,對x為二階連續可微的函數.對于任意的φ∈C以及t∈τ,約定對于任給的V ∈C1,2(τ×d×S)以及φ∈C,定義V:τ×d×S→如下. (5) 這里 E|x(t;ξ)|p≤α‖ξ‖p0e-βt, ?t≥-τ, 則稱方程(1)的解p階矩指數穩定. 證明不妨設T>0適當小,使得 其中D2=為正常數;L=(顯然L>0).固定初值ξ,定義Picard迭代序列如下: (6) 首先驗證{xn(t)}定義合理、連續,且xn(t)∈2([0,T];d). 這與文獻[5]定理3.1.2之證類似,從略. 接著證明{xn(t)}在空間2([0,T];d)中范數收斂.為此,只要歸納地證明以下不等式: bδn,n≥0, (7) b=bδ0. 今設Mn-1≤bδn-1(n≥1),則 h2(s,xn-1s-,y,r(s))]N(ds,dy)|2}≤ h1(s,xn-1s-,y,r(s))|2ν(dy)ds]+ h2(s,xn-1s-,y,r(s))|2ν(dy)ds]≤ 故(7)式得證.由(7)式推出{xn(t)}是2([0,T];d)中的Cauchy序列,故其范數收斂于某個x(t)∈2([0,T];d). 于是由Borel-Cantelli引理推出,a.s.地,有 推出所要結論.從而如文獻[5]中定理3.1.2之證,可說明x(t)是方程(1)的具有初值ξ的解. H(T)E[ds. (8) 采用一個停時論證.令τn=T∧inf{t∈[0,T],‖xt‖≥n},只需以τn∧t代t證(8)式.但為記號簡便,仍記τn∧t為t.此外約定f(t)=f(t,xt,r(t)),g(t)=g(t,xt,r(t)),hi(t)=hi(t,xt-,y,r(t))(i=1,2),則 K(T)E( 故得 1+K(T)≤1+ 然后用Gronwall不等式,即得所證. 引理1.2給出了方程(1)局部解的存在唯一性.類似文獻[10]定理3.3存在性的證明與引理1.2唯一性的證明,可得如下全局解存在唯一性定理. 定理 2.1假設(A1)~(A4)成立且p>1.此外,假設存在一個函數V∈C1,2(τ×d×S)滿足(i) ~(iii) . (i) 存在正常數c1、c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ?(t,x,i)∈τ×d×S; (9) (ii) 存在常數l0∈(0,1),使得對任意的t∈0及有不等式 E|D(t,φ,i)|p≤lp0‖φ‖p0; (10) (11) 有 成立. 即方程(1)的零解p階矩指數穩定. 證明對于任意有界初值ξ,要證(12)式成立,只需證明當0<γ<μ∧τ-1ln時,不等式成立: m(t)eγtE|x(t)|p≤β(1-κ1)-p, ?t≥0, (13) 注意到,如果成立 (14) 則對t≥0時,利用條件(ii),有 M(t) κ1-p1E|D(s,xs,r(s))|p]≤ κ1-p1lp0eγs‖xs‖p0]≤ β(1-κ1)1-p+κ1M(t). (15) 于是M(t)≤β(1-κ1)-p<βq1e-γτ.因為m(t)≤M(t),因而只需要證明(14)式,即可得(13)式成立. 下面證明(14)式成立.為此需證 W(t)e ?t≥0. (16) 由條件(ii)得 c2(1+l0)p-1[E|ξ(0)|p+ l01-pE|D(0,ξ,r(0))|p]≤ c2(1+l0)p‖ξ‖p0=βc1, 下用反證法.假設(16)式不對所有的t≥0成立,則必有最小的t1∈0,及充分小的δ>0,使得 W(t)≤βc1, ?t∈[0,t1), W(t1)=βc1,W(t1+δ)>W(t1). 因為對任給的t∈[t1-τ,t1],當t≥0時,有 EV(t,x(t),r(t))≤c2E|x(t)|p= c2e-γtm(t)≤c2e-γtM(t) (17) 當t<0時,由γ與β的取值、W(t)的定義以及不等式(1-κ1)-p EV(t,x(t),r(t))≤ 從而有 E[V(t1,x(t1),r(t1))]< 因此,由r(t)的定義,對任意的t>0以及對充分小的δ′>0,有 EV(t,x ?t∈[t1,t1+δ′). (19) 另一方面,對任意充分小的δ″>0,由V的定義以及It公式,有 r(s))g(s,x(s),r(s))]ds+ h1(s-,x(s-),y,r(s-)),r(s-))- h1(s-,x(s-),y,r(s-)),r(s-))- h2(s-,x(s-),y,r(s-)),r(s-))- (20) 令 M(δ″) h1(s-,x(s-),y,r(s-)),r(s-))- 顯然M(δ″)是一個連續的局部鞅[11]. 對(20)式左右兩邊同時取期望,有 W(t1+δ″)-W(t1)= EV(t,xt,r(t))]dt≤0, 從而W(t1+δ″)≤W(t1),與t1的“最小性”相矛盾.因此,(16)式必對任何的的t≥0成立,于是(12)式成立.證畢. 在定理2.1的證明過程中,使用了如下事實: EV(t+θ,x(t+θ),r(t+θ))≤ 如果上述事實被 EV(t+θ,x(t+θ),r(t+θ))≤ 或者 EV(t+θ,x(t+θ),r(t+θ))≤ 所取代,則建立如下定理. 定理 2.2假設(A1)~(A4)成立且p>1.此外,假設存在一個函數V∈C1,2(τ×d×S)滿足(i)~(iii). (i) 存在正常數c1,c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ?(t,x,i)∈τ×d×S; (21) (ii) 存在常數l0∈(0,1),使得對任意的t∈0及有不等式 E|D(t,φ,i)|p≤lp0‖φ‖p0; (22) 對所有t≥0,有 定理 2.3假設(A1)~(A4)成立且p>1.此外,假設存在一個函數V∈C1,2(τ×d×S)滿足(i)~(iii). (i) 存在正常數c1,c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ?(t,x,i)∈τ×d×S; (23) (ii) 存在常數l0∈(0,1),使得對任意的t∈0及成立不等式: E|D(t,φ,i)|p≤lp0‖φ‖p0; (24) 對所有t≥0,有 考慮如下具Markov切換與Lévy噪聲的中立型隨機時滯微分方程 定理 3.1設p>1,且假設存在一個函數V∈C1,2(τ×d×S)滿足(i)~(iv). (i) 存在正常數c1、c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ?(t,x,i)∈τ×d×S; |D(t,x(t-δ0(t)),x(t-δ1(t)),…, x(t-δl(t)),r(t))|p≤ (26) φ(-δ1(t)),…,φ(-δl(t)),i)+ G(t,φ(0),φ(-δ1(t)),…,φ(-δl(t)),i)]+ φ(-δ1(t)),…,φ(-δl(t)),y,i),i)- φ(-δ1(t)),…,φ(-δl(t)), (27) 證明由(5)式函數V的定義可得: V(t,φ,i)= φ(-δl(t)),i)+ G(t,φ(0),φ(-δ1(t)),…,φ(-δl(t)),i)]+ H1(t,φ(0),φ(-δ1(t)),…,φ(-δl(t)),y,i) 成立,其中q是滿足條件(iv)的常數,則由條件(iii)可得: E|D(t,x(t-δ0(t)),x(t-δ1(t)),…, x(t-δl(t)),r(t))|p≤ 因此,定理2.1的條件(ii)成立.這樣,由定理2.1得方程(25)的零解p階矩指數穩定.證畢. 特別地,考慮如下具Markov切換與Lévy噪聲的中立型線性隨機時滯微分方程 (A5) 存在常數εi(i=1,2,…,6),使得: 推論 3.2假設條件(A5)成立外,若存在正常數q,ai(i=1,2,…,n)以致ρ0<0,ρ1>0,ρ0+qρ1<0,并且 其中 其中I為d×d的單位矩陣.則方程(28)的零解均方指數穩定. 證明取Lyapunov函數為V(t,x,i)=ai|x|2,其中ai(i=1,2,…,n)為正常數,易驗證定理3.1的條件成立,從而結論成立. 例 3.3考慮如下具Markov切換與Lévy噪聲的中立型隨機時滯微分方程 其中,x(t)=(x1(t),x2(t))T,w(t)是一個二維的布朗運動,{r(t),t≥0}是取值于有限狀態S={1,2}的右連續Markov鏈,生成算子sint+0.3. 此外 并假設: 取Lyapunov函數為V(t,x,i)=ai|x|2,其中a1=0.6,a2=0.7.于是p=2,q的取值范圍為:q>1.168 9. 不妨取q=2,經計算得ρ0=-4.249 4<0,ρ1=0.908 1>0且ρ0+qρ1=-2.433 2<0. 因此,由推論3.2得方程(29)的零解均方指數穩定.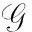

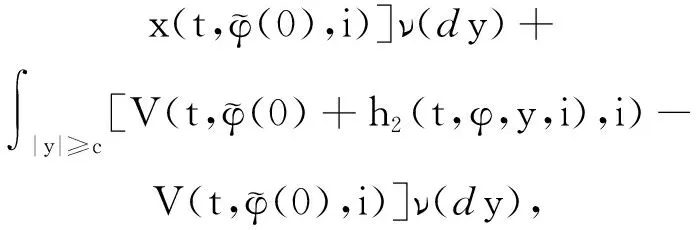
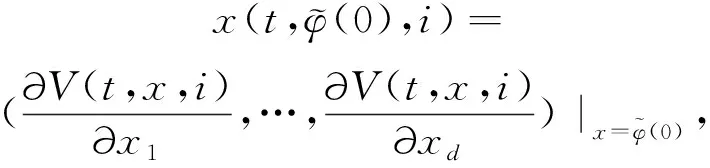

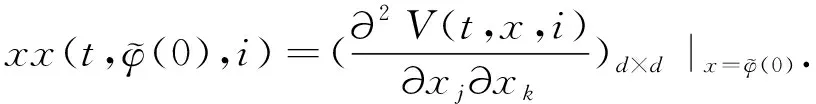
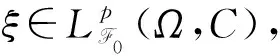
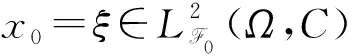
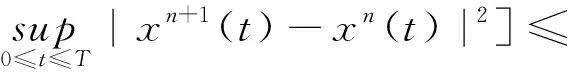
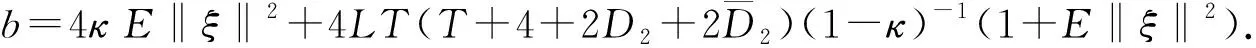

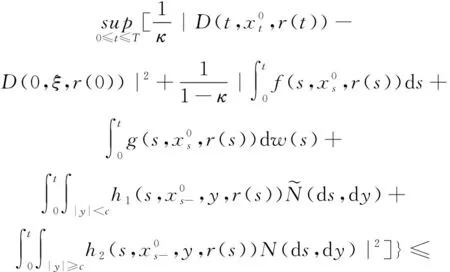
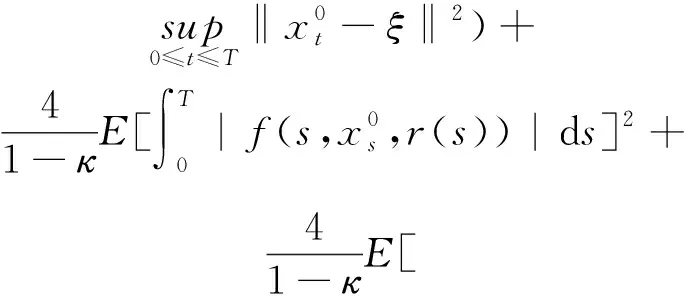
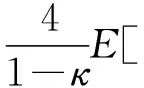
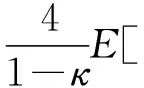
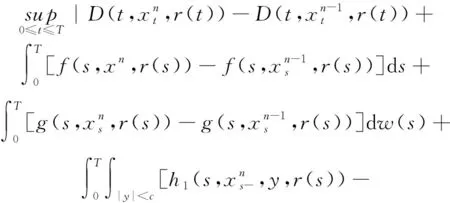
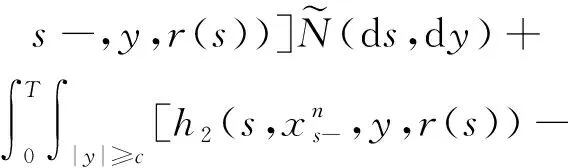
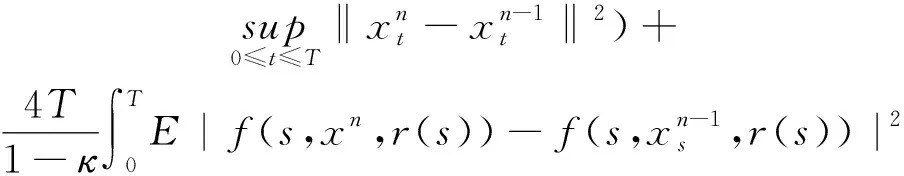
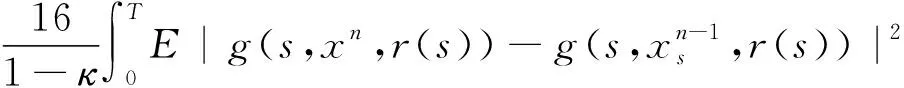
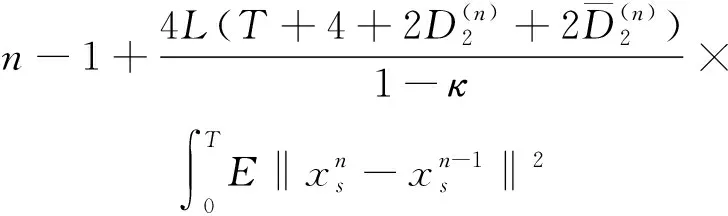
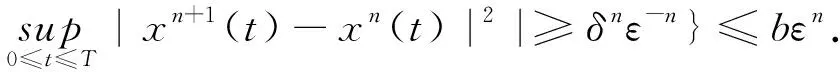




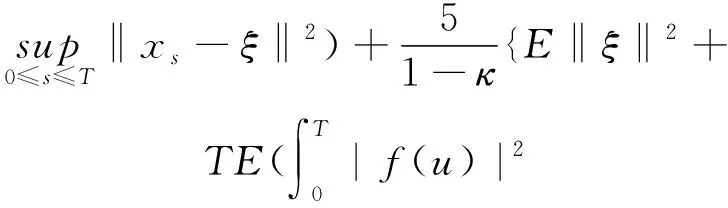
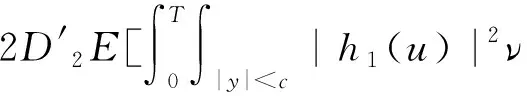
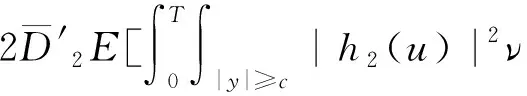
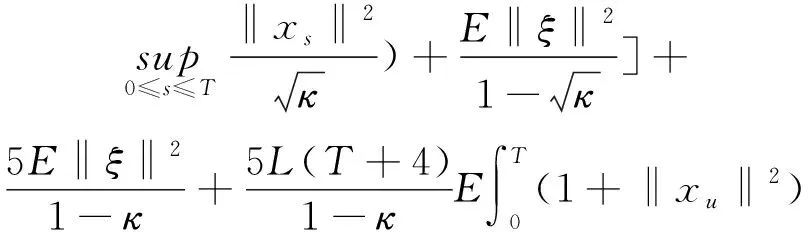


2 主要結果
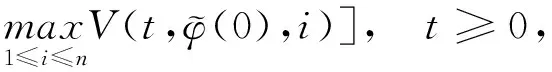
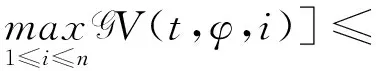
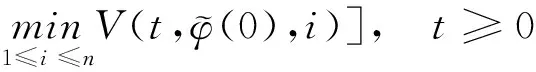
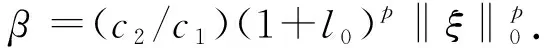

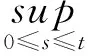
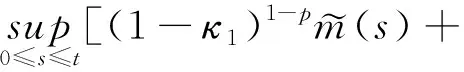

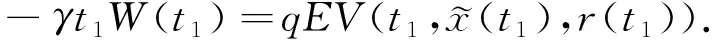
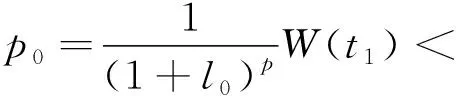
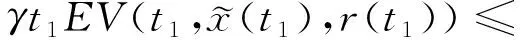

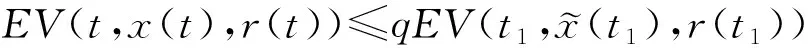
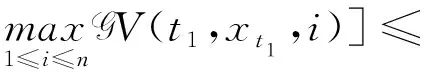
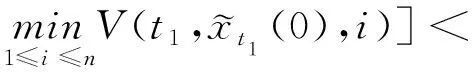
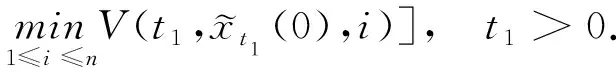
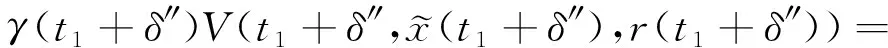
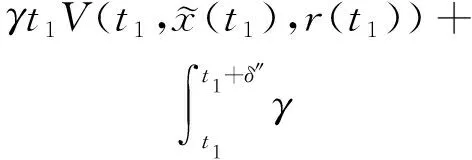
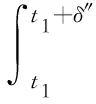
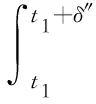
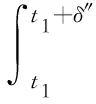
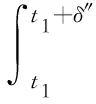
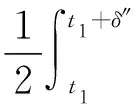

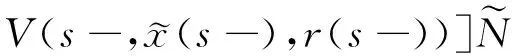

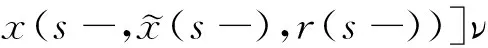
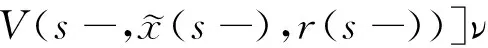
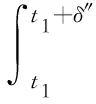

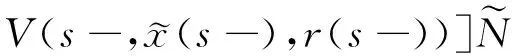
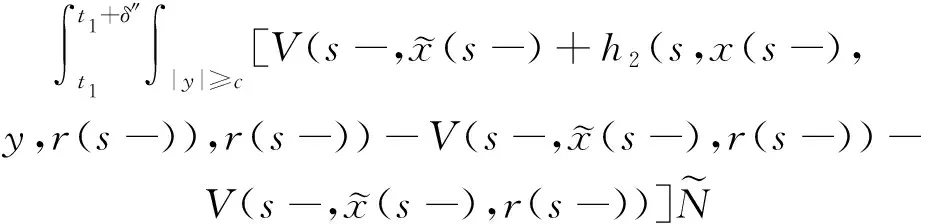
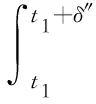
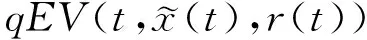
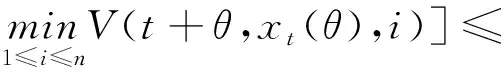

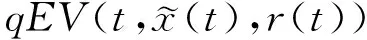
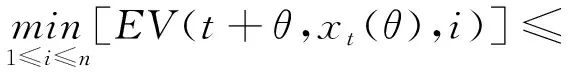

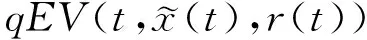
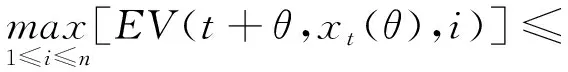
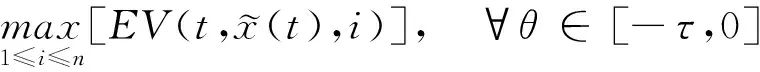
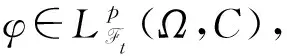
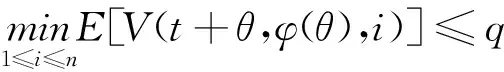
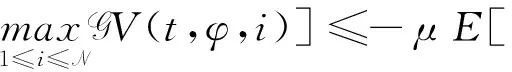
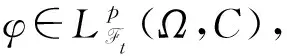
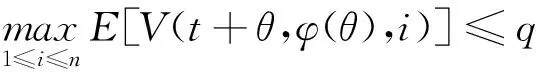
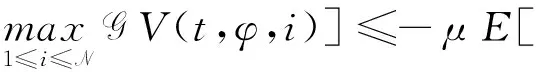
3 應用