數(shù)學(xué)運(yùn)算核心素養(yǎng)視角下的“三角函數(shù)”試題分析

許雅楠 黃在堂 孫艷雷 陳美賢

[摘 ?要] 數(shù)學(xué)運(yùn)算素養(yǎng)是影響學(xué)生高中數(shù)學(xué)學(xué)習(xí)的一個(gè)重要因素，所以選擇恰當(dāng)?shù)姆椒▽?duì)學(xué)生現(xiàn)階段數(shù)學(xué)運(yùn)算素養(yǎng)落實(shí)情況進(jìn)行考查是很有必要的. 在此基礎(chǔ)上，以SOLO分類理論為指導(dǎo)，根據(jù)2016—2020年五年天津高考理科數(shù)學(xué)試卷所考查的“三角函數(shù)”知識(shí)點(diǎn)對(duì)數(shù)學(xué)運(yùn)算素養(yǎng)水平進(jìn)行劃分，得到這五年天津高考對(duì)學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)水平的要求，并由此給出提高學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)的一些教學(xué)建議.

[關(guān)鍵詞] 數(shù)學(xué)運(yùn)算;三角函數(shù);試題分析;SOLO分類理論

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》中提出了高中數(shù)學(xué)六大核心素養(yǎng)，分別是數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運(yùn)算和數(shù)據(jù)分析，并強(qiáng)調(diào)學(xué)科核心素養(yǎng)是育人價(jià)值的集中體現(xiàn)，是學(xué)生通過高中數(shù)學(xué)學(xué)習(xí)而逐步形成的正確價(jià)值觀、必備品格和關(guān)鍵能力[1]. 其中數(shù)學(xué)運(yùn)算能力的提高不但可以幫助學(xué)生提升數(shù)學(xué)學(xué)習(xí)的邏輯思維能力和空間想象能力，還是提高學(xué)生數(shù)學(xué)建模能力的有效途徑，所以對(duì)學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)落實(shí)情況的考查是很有必要的. 考查學(xué)生核心素養(yǎng)落實(shí)情況最有效的途徑就是高考. 三角函數(shù)作為高考的必考內(nèi)容，它是高中學(xué)習(xí)的一類重要的函數(shù)，涉及內(nèi)容偏多，形式抽象，需要學(xué)生具有較強(qiáng)的抽象能力和概括能力. 同時(shí)，三角函數(shù)的學(xué)習(xí)內(nèi)容與之前函數(shù)的學(xué)習(xí)內(nèi)容共同形成了龐大的函數(shù)知識(shí)體系，所以三角函數(shù)一直在高考中占有重要的地位. 因此考查學(xué)生的數(shù)學(xué)運(yùn)算這一核心素養(yǎng)的落實(shí)情況可以借助于2016—2020年五年天津高考理科數(shù)學(xué)試卷（下文簡(jiǎn)稱為“2016—2020年天津高考卷”）中與三角函數(shù)相關(guān)的試題進(jìn)行分析，根據(jù)SOLO分類理論所劃分的單一結(jié)構(gòu)層次、多元結(jié)構(gòu)層次、關(guān)聯(lián)結(jié)構(gòu)層次和抽象拓展結(jié)構(gòu)層次等四個(gè)層次來分析相關(guān)試題中表現(xiàn)的數(shù)學(xué)運(yùn)算素養(yǎng)處于哪個(gè)水平，并給出提高學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)的一些教學(xué)建議.

相關(guān)概念界定

1. 數(shù)學(xué)運(yùn)算素養(yǎng)

數(shù)學(xué)運(yùn)算主要表現(xiàn)為理解運(yùn)算對(duì)象、掌握運(yùn)算法則、探究運(yùn)算思路和求得運(yùn)算結(jié)果這四個(gè)方面，它是學(xué)生在明確運(yùn)算對(duì)象的基礎(chǔ)上，依據(jù)運(yùn)算法則解決數(shù)學(xué)問題的一種數(shù)學(xué)素養(yǎng)，是解決數(shù)學(xué)問題的基本手段[1]. 通過高中的數(shù)學(xué)課程學(xué)習(xí)，學(xué)生能夠根據(jù)具體的數(shù)學(xué)問題采用適當(dāng)?shù)臄?shù)學(xué)運(yùn)算方法，并在借助于數(shù)學(xué)運(yùn)算能力解決實(shí)際問題的過程中進(jìn)一步提高自身數(shù)學(xué)運(yùn)算能力和數(shù)學(xué)思維的發(fā)展. 數(shù)學(xué)運(yùn)算在一定程度上反映了學(xué)生的數(shù)學(xué)素養(yǎng)，數(shù)學(xué)運(yùn)算的過程滲透著其他五個(gè)核心素養(yǎng)，數(shù)學(xué)運(yùn)算貫穿中學(xué)生整個(gè)學(xué)生時(shí)代，是學(xué)生學(xué)習(xí)和未來社會(huì)發(fā)展的必備能力及品質(zhì)[2].

2.SOLO分類理論

SOLO分類理論又稱為“可觀察的學(xué)習(xí)成果結(jié)構(gòu)”，它是基于皮亞杰的認(rèn)知發(fā)展理論建立起來的，并將皮亞杰有關(guān)認(rèn)知發(fā)展水平具有階段性的思想轉(zhuǎn)換到了具體的學(xué)習(xí)任務(wù)中，使得SOLO分類理論中的思維操作模式、學(xué)習(xí)周期和階段等概念均能得到合理的解釋，并由原來的“學(xué)習(xí)者的行為”的評(píng)價(jià)目標(biāo)轉(zhuǎn)化為“學(xué)習(xí)行為的結(jié)果”的評(píng)價(jià)目標(biāo)，從學(xué)習(xí)結(jié)果在結(jié)構(gòu)上的復(fù)雜程度來評(píng)價(jià)學(xué)生的學(xué)習(xí)質(zhì)量，從能力、思維操作、一致性與閉合、應(yīng)答結(jié)構(gòu)四個(gè)方面將學(xué)習(xí)行為的結(jié)果分成五個(gè)不同的層次，分別是前結(jié)構(gòu)層次、單一結(jié)構(gòu)層次、多元結(jié)構(gòu)層次、關(guān)聯(lián)結(jié)構(gòu)層次和抽象拓展結(jié)構(gòu)層次[3]. 這種方法使得評(píng)價(jià)目標(biāo)的界定更加清晰、準(zhǔn)確，從而提高了評(píng)價(jià)的信度與效度. 因此可以按照SOLO分類理論對(duì)2016—2020年天津高考卷中三角函數(shù)考點(diǎn)的相關(guān)試題進(jìn)行劃分. 由于思維水平處于前結(jié)構(gòu)層次的學(xué)生的作答通常表現(xiàn)為空白或者偏離到一些毫不相關(guān)的問題上，所以對(duì)于這一層次的相關(guān)試題的分析可以舍去，并將其他四個(gè)層次分別用U，M，R，E來表示，由此給出了對(duì)應(yīng)的數(shù)學(xué)運(yùn)算素養(yǎng)水平（如表1所示）：

試題分析

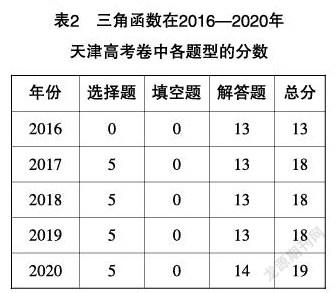
三角函數(shù)在2016—2020年天津高考卷中的題型分布情況——各題型的分?jǐn)?shù)（如表2所示）：

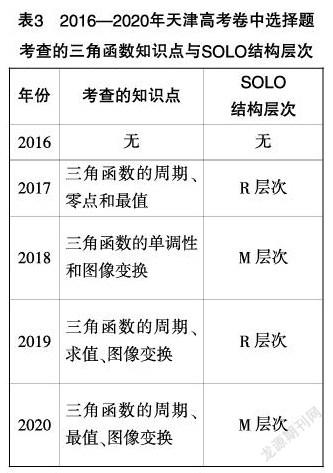
分析：這道題同樣考查了三個(gè)知識(shí)點(diǎn)：結(jié)論①是對(duì)三角函數(shù)周期的考查;結(jié)論②是對(duì)三角函數(shù)最值的考查;結(jié)論③是通過函數(shù)圖像上所有點(diǎn)的平移對(duì)三角函數(shù)圖像變換的考查. 由此可以看出，該題僅僅是對(duì)知識(shí)點(diǎn)應(yīng)用的簡(jiǎn)單考查，不要求學(xué)生將這些知識(shí)點(diǎn)聯(lián)系起來綜合應(yīng)用而解決問題.因此這個(gè)問題屬于多元結(jié)構(gòu)層次，數(shù)學(xué)運(yùn)算素養(yǎng)水平達(dá)到中等以上的學(xué)生能夠解答.

2. 解答題的分析

表4展示了2016—2020年天津高考卷中解答題考查的三角函數(shù)知識(shí)點(diǎn)以及對(duì)應(yīng)的SOLO結(jié)構(gòu)層次，通過每個(gè)層次結(jié)構(gòu)試題考查的知識(shí)點(diǎn)之間的關(guān)系來確定學(xué)生的數(shù)學(xué)運(yùn)算素養(yǎng)水平.

從解答題考查的三角函數(shù)知識(shí)點(diǎn)來看，近五年的天津高考卷主要考查的是正弦定理、余弦定理，同角三角函數(shù)的基本關(guān)系式，二倍角公式和兩角和與差的正弦、余弦公式. 根據(jù)每年天津高考卷對(duì)應(yīng)的SOLO結(jié)構(gòu)層次可以看出，解答題對(duì)三角函數(shù)的考查都處于關(guān)聯(lián)結(jié)構(gòu)層次（R層次），以中等難度的問題為主，對(duì)學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)水平的要求較高.

從表4中還可以看出，2020年天津高考卷考查了正弦定理、余弦定理，同角三角函數(shù)的基本關(guān)系式，二倍角公式，兩角和的正弦公式，需要學(xué)生熟練掌握這些知識(shí)點(diǎn)，并整體把握、綜合應(yīng)用，解決一些較為復(fù)雜的三角函數(shù)問題，處于SOLO結(jié)構(gòu)層次的關(guān)聯(lián)結(jié)構(gòu)層次，對(duì)數(shù)學(xué)運(yùn)算素養(yǎng)的要求較高. 同樣，2016—2019年三角函數(shù)解答題也屬于關(guān)聯(lián)結(jié)構(gòu)層次，需要學(xué)生具有較高的數(shù)學(xué)運(yùn)算素養(yǎng). 下面對(duì)2018年與2020年的關(guān)于三角函數(shù)的解答題進(jìn)行分析：

2018年天津高考卷（第15題，13分）：在△ABC中，內(nèi)角A，B，C所對(duì)的邊分別為a，b，c，已知bsinA=acosB-.

（1）求角B的大小;

（2）設(shè)a=2，c=3，求b和sin（2A-B）的值.

分析：該題主要考查的是正弦定理、余弦定理，兩角和與差的正弦公式，同角三角函數(shù)的基本關(guān)系式和二倍角公式. 由正弦定理可得bsinA=asinB，將其與bsinA=acosB-聯(lián)立，求出問題（1）中角B的值. 結(jié)合問題（1）的結(jié)果與余弦定理得到b的值，根據(jù)題目的條件與同角三角函數(shù)的基本關(guān)系式可以得到sinA和cosA的值，再利用二倍角公式得到sin2A和cos2A的值，最后根據(jù)兩角差的正弦公式得到sin（2A-B）的值. 所以將該題納入SOLO結(jié)構(gòu)層次的關(guān)聯(lián)結(jié)構(gòu)層次，對(duì)學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)水平的要求較高.

2020年天津高考卷（第16題，14分）：在△ABC中，角A，B，C所對(duì)的邊分別為a，b，c. 已知a=2，b=5，c=.

（1）求角C的大小;

（2）求sinA的值;

（3）求sin2A+的值.

分析：該題主要考查的是正弦定理、余弦定理，同角三角函數(shù)的基本關(guān)系式，二倍角公式以及兩角和的正弦公式. 先利用余弦定理求出問題（1）中角C的值，然后根據(jù)正弦定理=與角C的值求得sinA的值再利用問題（2）的結(jié)果與同角三角函數(shù)的基本關(guān)系式和二倍角公式得到sin2A與cos2A的值，最后由兩角和的正弦公式求得sin2A+的值. 由此可以看出，問題（2）和問題（3）都需要在前一小題的基礎(chǔ)上進(jìn)行解答，需要學(xué)生整體把握條件與問題得到最終的結(jié)果，因此該題同樣屬于關(guān)聯(lián)結(jié)構(gòu)層次.

總結(jié)

根據(jù)上述分析，我們不難發(fā)現(xiàn)2016—2020年天津高考卷中三角函數(shù)選擇題對(duì)于數(shù)學(xué)運(yùn)算素養(yǎng)的考查處于中等或較高水平，而這五年的天津高考卷中三角函數(shù)解答題從知識(shí)點(diǎn)、題型上看沒有太大變化，對(duì)數(shù)學(xué)運(yùn)算素養(yǎng)的考查一直處于較高水平. 因此，天津高考卷對(duì)三角函數(shù)的數(shù)學(xué)運(yùn)算素養(yǎng)的考查基本處于較高水平并將一直處于該水平. 同時(shí)，這五年天津高考卷注重考查學(xué)生對(duì)三角函數(shù)性質(zhì)、圖像、恒等變換以及解三角形需要的一些重點(diǎn)知識(shí)的運(yùn)用;重點(diǎn)考查學(xué)生對(duì)三角函數(shù)基本公式的靈活應(yīng)用，包括誘導(dǎo)公式，兩角和與差的正弦、余弦公式，正弦定理和余弦定理等;考查學(xué)生對(duì)三角函數(shù)知識(shí)的綜合運(yùn)用能力，全方面體現(xiàn)核心素養(yǎng)落實(shí)的情況. 如運(yùn)用基本公式對(duì)三角函數(shù)式進(jìn)行化簡(jiǎn)，注重學(xué)生對(duì)基本公式的靈活應(yīng)用以及準(zhǔn)確求解的能力，著重考查學(xué)生的數(shù)學(xué)運(yùn)算能力;如解三角形，要求學(xué)生能夠熟練掌握并靈活應(yīng)用基本公式或定理，根據(jù)題目中的已知條件進(jìn)行求解，需要學(xué)生具有較高的運(yùn)算能力. 三角函數(shù)不僅是一種特殊的函數(shù)，還是考查學(xué)生數(shù)學(xué)運(yùn)算能力的重要載體. 天津高考通過多樣化的三角函數(shù)知識(shí)相融合的方式命題，體現(xiàn)了試題的綜合性，有效地落實(shí)了學(xué)生的數(shù)學(xué)核心素養(yǎng).

教學(xué)建議

1. 理解相關(guān)概念，明確運(yùn)算對(duì)象

概念的深入理解可以幫助學(xué)生快速準(zhǔn)確地明確運(yùn)算對(duì)象，從而根據(jù)不同的運(yùn)算對(duì)象找到對(duì)應(yīng)的公式解決問題[4]. 如果學(xué)生沒有掌握所學(xué)對(duì)象的概念，那么數(shù)學(xué)核心素養(yǎng)也很難得到提升. 比如，若學(xué)生對(duì)于三角函數(shù)的基本概念不明確，就會(huì)導(dǎo)致三角函數(shù)的公式和定理學(xué)不好，面對(duì)問題時(shí)不能準(zhǔn)確地運(yùn)用相應(yīng)的公式、定理或法則進(jìn)行運(yùn)算，從而運(yùn)算素養(yǎng)很難提升. 因此，教師在課堂中要注重?cái)?shù)學(xué)概念的教學(xué). 首先教學(xué)開始要注意讓學(xué)生掌握概念的外延和適用的范圍，適當(dāng)給出一些比較容易混淆的相關(guān)概念讓學(xué)生能夠辨析;其次可以設(shè)定適合的情境，引導(dǎo)學(xué)生主動(dòng)探究概念，從多個(gè)角度理解概念并建立起相關(guān)概念之間的聯(lián)系，形成知識(shí)圖式，加深學(xué)生對(duì)概念的理解，從而提高學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng).

2. 準(zhǔn)確記憶公式，靈活應(yīng)用變式

數(shù)學(xué)公式是人們研究某個(gè)對(duì)象與其他對(duì)象間所得到的某種規(guī)律，數(shù)學(xué)公式產(chǎn)生的過程中包含著大量的數(shù)學(xué)思想、豐富的數(shù)學(xué)方法[5]. 高中學(xué)習(xí)的數(shù)學(xué)公式數(shù)量多且煩瑣，學(xué)生容易出現(xiàn)記不清公式或運(yùn)用不恰當(dāng)?shù)那闆r，對(duì)學(xué)生的數(shù)學(xué)運(yùn)算會(huì)產(chǎn)生很大的影響，甚至?xí)绊憣W(xué)生的數(shù)學(xué)學(xué)習(xí). 高考不是對(duì)數(shù)學(xué)公式簡(jiǎn)單的考查，而是通過變式的方式考查學(xué)生是否真正理解了數(shù)學(xué)公式的內(nèi)涵. 因此，在數(shù)學(xué)公式的新授課上，教師不能一味地采用灌輸式教學(xué)，而是要引導(dǎo)學(xué)生經(jīng)歷并理解公式的推導(dǎo)過程，這樣學(xué)生才能更好地學(xué)會(huì)公式的正向、逆向或變式使用，促進(jìn)學(xué)生數(shù)學(xué)思維的發(fā)展，加深對(duì)公式的記憶，提高數(shù)學(xué)運(yùn)算素養(yǎng)水平. 比如，在三角函數(shù)教學(xué)時(shí)，教師可以通過單位圓的對(duì)稱性引導(dǎo)學(xué)生推導(dǎo)出誘導(dǎo)公式，讓學(xué)生通過推導(dǎo)的過程熟記公式并能夠靈活應(yīng)用.

3. 提高學(xué)生興趣，培養(yǎng)探究能力

高中數(shù)學(xué)內(nèi)容比起初中更加抽象、不容易理解，這就需要學(xué)生增強(qiáng)自身獨(dú)立思考和探究的能力，而學(xué)生思考和探究的動(dòng)力往往源于他們對(duì)知識(shí)的好奇心和興趣. 只有當(dāng)學(xué)生愿意學(xué)數(shù)學(xué)，才會(huì)對(duì)數(shù)學(xué)問題獨(dú)立思考，在運(yùn)算的過程中探究更多簡(jiǎn)便的運(yùn)算途徑，提高自身數(shù)學(xué)運(yùn)算素養(yǎng)水平. 因此，教師在數(shù)學(xué)教學(xué)的過程中可以將數(shù)學(xué)與生活相結(jié)合，讓學(xué)生感受到數(shù)學(xué)的實(shí)用性，從而培養(yǎng)他們的思考能力與探究能力，同時(shí)也能夠幫助學(xué)生更好地學(xué)習(xí)其他科目[6]. 比如在講解三角函數(shù)時(shí)可以聯(lián)系數(shù)學(xué)史，通過講述三角函數(shù)的發(fā)展歷史，幫助學(xué)生深入理解三角函數(shù)的概念，引起學(xué)生的數(shù)學(xué)學(xué)習(xí)興趣.

4. 聚焦數(shù)學(xué)知識(shí)，提升學(xué)科素養(yǎng)

數(shù)學(xué)知識(shí)是學(xué)生解決實(shí)際問題的工具，而數(shù)學(xué)學(xué)科核心素養(yǎng)的形成和發(fā)展是在學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)和內(nèi)化數(shù)學(xué)知識(shí)的過程中進(jìn)行的. 作為一名數(shù)學(xué)教師，要以發(fā)展學(xué)生的學(xué)科核心素養(yǎng)為教學(xué)目標(biāo)，這就要求教師在理解高中數(shù)學(xué)核心素養(yǎng)內(nèi)涵的基礎(chǔ)上，了解學(xué)科知識(shí)的要求和學(xué)生的認(rèn)知發(fā)展水平，根據(jù)教材合理地安排教學(xué)內(nèi)容，創(chuàng)設(shè)問題情境，引導(dǎo)學(xué)生自主探究，從而幫助學(xué)生充分理解數(shù)學(xué)知識(shí). 在數(shù)學(xué)知識(shí)的學(xué)習(xí)中提高學(xué)生的理性思維和解決問題的能力，將學(xué)科核心素養(yǎng)的培養(yǎng)落實(shí)到每堂數(shù)學(xué)課中，提高學(xué)生的數(shù)學(xué)思維水平，使學(xué)生學(xué)會(huì)用數(shù)學(xué)的眼光看世界.

參考文獻(xiàn)：

[1] ?中華人民共和國(guó)教育部. 普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）[S]. 北京：人民教育出版社，2018.

[2] ?陳秋嬋. 基于SOLO理論的高中生數(shù)學(xué)運(yùn)算素養(yǎng)的發(fā)展研究[D]. 閩南師范大學(xué)，2020.

[3] ?彼格斯. 學(xué)習(xí)質(zhì)量評(píng)價(jià)[M]. 人民教育出版社，2010.

[4] ?王雪嬌. 深度學(xué)習(xí)視域下高中生數(shù)學(xué)運(yùn)算素養(yǎng)提升的策略研究[D]. 哈爾濱師范大學(xué)，2020.

[5] ?閆惠澤. 基于波利亞解題思想的高中數(shù)學(xué)公式的教學(xué)研究[D]. 遼寧師范大學(xué)，2020.

[6] ?崔妮娜. 高中生三角函數(shù)學(xué)習(xí)障礙調(diào)查與教學(xué)策略的研究[D]. 陜西師范大學(xué)，2019.