『扶』『放』內化自主建構
——《正比例的意義》教學設計

文 張煒

【教學內容】

蘇教版六年級下冊第56、57頁。

【教學過程】

一、“引”——激趣感知，認識概念

1.感受“相關聯”。

出示資料一：小丑魚又稱海葵魚，它與海葵有著密不可分的共生關系。帶毒刺的海葵保護小丑魚，小丑魚消化后的殘渣則為海葵提供了食物。因此，海葵越多的地方，小丑魚也就越多；小丑魚減少，海葵也會受到影響而減少。

出示資料二：在草原上，狼以羊為食，狼的數量增多，會造成羊的數量減少；反之，狼的數量減少，羊的數量會隨之增加，兩者互為因果，此消彼漲，此漲彼消，維持著生態的平衡。

師：從這兩個有趣的現象中，你發現了什么？

預設：第一個現象中，海葵的數量變化會導致小丑魚的數量變化。第二個現象中，狼的數量變化會導致羊的數量變化。

師：你能具體說說，兩者數量是如何變化的嗎？

預設：海葵的數量增加，小丑魚的數量也增加；海葵的數量減少，小丑魚的數量也減少。狼的數量增加，羊的數量減少；狼的數量減少，羊的數量會增加。

師：也就是說，這兩個量是相互影響的，一個量變化，另一個量也會隨著變化。在數學上，把這樣兩個互相影響的量叫作兩個“相關聯的量”。比如，海葵的數量和小丑魚的數量就是兩個相關聯的量。

2.體會正向、反向變化。

對比：上面兩個現象中，它們的變化有區別嗎？

預設：海葵的數量增加，小丑魚的數量也增加，是跟著一起變的；而狼的數量增加，羊的數量卻減少，是反過來變的。

師：海葵和小丑魚的數量變化是相同的，叫作正向變化；而狼和羊的數量變化是相反的，叫作反向變化。

二、“扶”——引導建構，理解概念

1.認知規律。

師：除了自然界，在科技發達的人類社會里也存在這樣的現象：一輛汽車在公路上行駛，行駛時間和路程如下表：

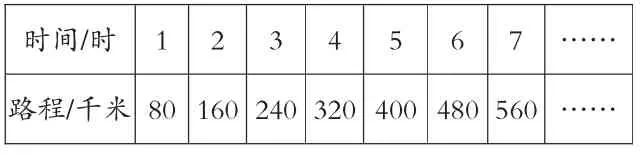
時間/時 1 234567 ……路程/千米80 160 240 320 400 480 560 ……

師：觀察表格，你有什么發現？

預設：時間增加，路程也隨著增加。

師：你能具體說說嗎？

預設：時間從1 小時、2 小時、3 小時……增加，路程也從80 千米、160 千米、240 千米……增加。

明確：時間和路程是兩個相關聯的量，行駛時間增加，路程也隨著增加；反過來，時間減少，路程也隨著減少。兩個量是正向變化的。

師：在這樣的變化中，有不變的嗎？

預設：相對應的路程除以時間的商不變。80÷1=80、160÷2=80、240÷3=80、320÷4=80、400÷5=80、480÷6=80、560÷7=80。

師：我們學過比的內容了，你能把路程除以時間用比的形式描述并求比值嗎？

師：這里路程和時間比的比值都是80，比值80 是什么呢？

明確：路程與對應時間的比的比值是速度。

師：現在你能完整說說路程、時間、速度的變化情況了嗎？

明確：時間和路程是兩個相關聯的量，時間變化，路程也隨之變化，但路程和時間的比值即速度不變。

2.理解概念。

師：你能用一個式子來表示路程、時間、速度這三個量的關系嗎？先想一想，再和同桌交流。

對比優化：這三個式子都清晰地反映了路程、時間、速度的關系，對比第（1）個式子，第（2）個式子針對表格數據更具體，第（3）個式子更具有一般性，能夠反映所有速度不變的情況。

談話：第（3）個式子揭示了路程、時間、速度三個量的本質關系，也非常接近數學上相關概念的定義。數學上，用來表示，“一定”即不變的意思。請看教材第56 頁最下面一段話。

預設：路程和時間成正比例關系。

明確：路程和時間是兩種相關聯的量，時間變化，路程也隨著變化。當路程和相對應時間的比的比值總是一定（即速度一定）時，行駛的路程和時間成正比例關系，行駛的路程和時間是成正比例的量。

師：現在你知道正比例關系的意思了吧，這就是今天要學習的內容——“正比例的意義”（揭題）。

三、“放”——遷移對比，深化概念

1.自主探究，深化理解。

師：其實在我們的生活中就有這種關系。比如：你在購買一種鉛筆時，數量和總價的情況如下表：

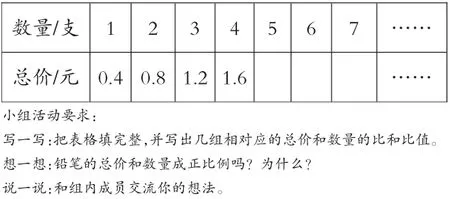
師：誰來說說你們組的想法？

預設：鉛筆的總價和數量成正比例關系，因為總價和數量的比值不變，都是0.4。

提問：這個0.4 表示什么？

預設：鉛筆的單價。

追問：能用一個式子表示嗎？

師：那總價和數量相關聯嗎？

預設：（1）總價和數量是兩個相關聯的量，數量變化，總價也隨著變化；（2）總價和數量是兩個相關聯的量，總價變化，數量也隨著變化。

師：這兩個說法你認可哪一個？為什么？

預設：第一個，因為總價是隨著數量的變化而改變的，數量變化才導致總價的變化。

明確：總價和數量是兩個相關聯的量，數量變化，總價也隨著變化。當總價和相對應數量的比值一定（也就是單價一定）時，總價和數量成正比例關系，總價和數量是成正比例的量。

2.辨別區分，提煉模型。

（1）判斷分析。

師：你能像老師這樣，舉幾個生活中成正比例關系的例子嗎？

預設：①單價8 元一本，訂雜志的總價和數量；②人的身高和體重；③一本書120 頁，已讀頁數和剩余頁數；④生產衣服的總數和工作時間；⑤年齡相差25 歲，我的年齡和爸爸的年齡；⑥全班48 人分組做游戲，分組時每組人數和組數。

師：他們舉的例子都是正比例關系嗎？

小組活動要求：想一想：你舉的例子中兩個量成正比例關系嗎？為什么？寫一寫：利用空表格和組內成員創造幾組數據，寫出相對應的比，并求出比值。說一說：交流你的想法。

分層交流:

第一層：“真”正比例關系。

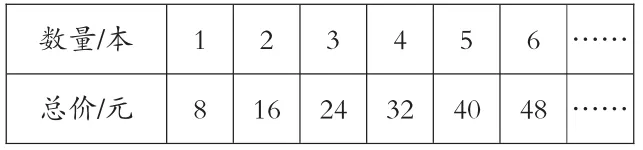
數量/本123456 ……總價/元816 24 32 40 48 ……

明確：總價和數量是兩個相關聯的量，數量變化，總價也隨著變化，。所以是兩個相關聯的量，且比值一定。

第二層：“假”正比例關系。

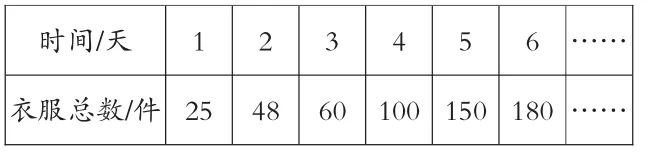
?時間/天123456 ……衣服總數/件 25 48 60 100 150 180 ……

明確：時間和總數是兩個相關聯的量，時間變化，總數也隨著變化，但是，總數和時間的比值是變化的，不是正比例關系。

第三層：“像”正比例關系。

錯例①。

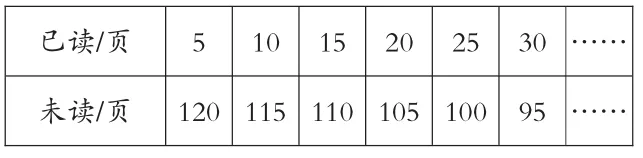
?已讀/頁510 15 20 25 30 ……未讀/頁120 115 110 105 100 95 ……

已讀頁數+剩余頁數=總頁數（一定），和一定，不是正比例關系。

錯例②。

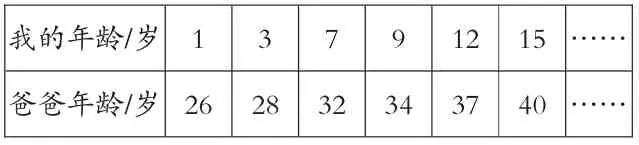
我的年齡/歲 137912 15 ……爸爸年齡/歲 26 28 32 34 37 40 ……?

爸爸年齡-我的年齡=年齡差（一定），差一定，不是正比例關系。

錯例③。

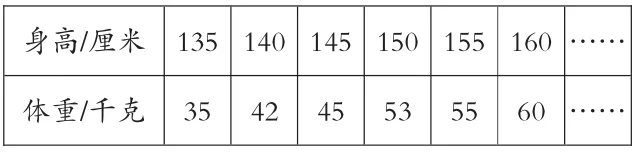
images/BZ_62_986_726_1098_778.png身高/厘米 135 140 145 150 155 160 ……體重/千克 35 42 45 53 55 60 ……

身高和體重不是相關聯的量，不是正比例關系。

錯例④。

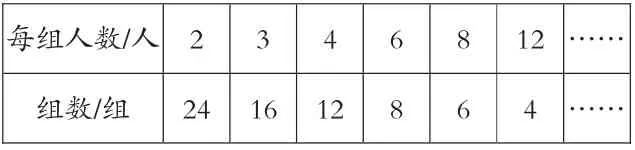
?每組人數/人 2346812 ……組數/組24 16 12864 ……

每組人數和組數是相關聯的量，但每組人數×組數=總人數，積一定，不是正比例關系。

談話：其實這是我們后面要學到的反比例關系。

對比：與“真”正比例關系相比，其他幾個例子有什么區別？

提問：是否為正比例關系，只要存在“一定”不變的量的式子就可以判斷了嗎？

預設：要先判斷兩個量是不是相關聯的。

明確：必須滿足①兩個量是相關聯的量，一個量變化，另一個量也隨之變化；②兩個量的比的比值一定不變。

小結：在判斷是否為正比例關系時，判斷的依據需要首先看是否為相關聯的兩個量，其次再判斷這兩個量的比的比值是否一定，才能斷定。

（2）概括模型。

觀察這幾個式子：

師：這幾個式子有什么相同點嗎？

預設：①都是比的形式；②都是相關聯的量；③比值都是一定的。

師：如果用x 和y 表示兩種相關聯的量，用k 表示它們的比值，你能用一個式子表示正比例關系嗎？

四、“結”——回顧反思，延伸概念

談話：今天我們學習了正比例的意義，誰能說說成正比例的量具有怎樣的關系？回顧研究的過程你有哪些體會？

（用PPT 呈現思維流程圖，帶領學生回顧整節課）

師：在我國古代就發現相關聯量的聯系，比如水漲船高、唇亡齒寒、舟隨潮起、泥多佛大等。當這兩個相關聯的量成正比例關系時，就可以產生解決實際問題的方法。（視頻播放“測量金字塔高度”的故事）

延伸：看了古希臘的哲學家泰勒斯測金字塔的故事后，如果要測一棵大樹的高度你會解決嗎？課后與組員一起研究。