理解：從“發現”到“遷移”的腳手架
——例談促進學生理解的教學設計策略

周曉萍

在日常教學中，我們經常會有這樣的體驗，課堂上學生似乎對所學知識已經掌握得比較好了，但課后練習效果卻并不理想。這一現象說明課堂上“掌握得較好”是個假象，那只是一種淺層的“發現”和模仿而已，學生對所學知識并未真正理解、內化。教學中教師要努力為學生搭建“理解”的腳手架，引導他們將所學知識技能遷移到新的問題情境中，從而解決實際問題。

一、優化方式，舉一反三

一次單元測試中，有這樣一道題：“一支籃球隊三場比賽的平均得分為105分，要使平均分達到120分，第四場應得（ ）分。”班上47名學生，僅有28名學生解答正確，正確率僅59.6%。這類題型在測試前學生已經練習過，已總結出這類題的數量關系是“第四場得分=四場總分－三場總分”。單元測試中正確率依然偏低意味著有相當一部分學生對這一數量關系的理解不到位或者根本沒理解。于是筆者及時調整了教學策略，優化了講評方式——

第一層次：讓解答正確的學生闡釋“120×4－105×3”這一算式的每一步分別表示什么，喚起大部分學生對解答該題基本數量關系的記憶。

第二層次：引導學生用畫圖的形式換個角度去理解（如圖1）。

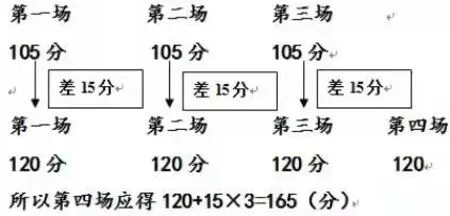
圖1

第三層次：改變該題的應用情境，編題：“吳××（班上的一名學生）若在最近的單元測試中語文和數學兩門平均分是70分，如果他想讓語數英三門的平均成績達到75分，那么他在接下來的英語測試中需要獲得（ ）分？”包括吳同學在內的全班絕大部分學生都正確解答出了這道題，并且大部分學生用的是第二種解題思路。

第四層次：你能編一道類似的考題嗎？

針對該教學環節進行的三個方面的優化，有效促進了學生對知識點的理解，提高了他們的舉一反三的能力。

一是轉換角色，以學生能理解的方式解析

此類題中的數量關系對于大部分學生而言是比較難理解的，于是，當教師站在學生的角度去思考問題，以邊畫圖邊解析的比較直觀的方式去引導學生分析數量關系時，他們一下子就明白了。理解了解法二的思路，又促進他們進一步去理解解法一的思路，于是數量與數量之間的關系就明晰了，理解也就真正達成了。

二是改變應用情境，用學生能理解的內容鋪陳

第三層次以學生身邊的實際例子即吳姓同學作為題材引入題目，則一下子打開了學生思維的閘門，他們很容易地把數學模型從題目的細節中抽取出來，從而利用平均數的知識順利地解答該題。這也再次表明，緊密聯系學生的生活實際優選教學內容，是促進學生理解的重要策略之一。

三是鼓勵參與，將學生卷入深度理解的場域

在解決問題的教學中，為幫助學生正確理解數量關系，改編數據、情節、問題結構等，以題組形式呈現是常用的方法，本環節也是通過改編不斷強化學生對一類題的基本數量關系的理解。特別重要的是，改編的主體由教師的示范引領轉入學生的全員參與，在那一刻，會編題、能解答出同學所出的題既是對學生知識掌握程度的再度考查，也是一次學法指導的良機。這一形式本身也是促進他們深度理解的又一手段，“舉一反三”“變中求不變”等數學思想方法得以無痕滲透。

二、深化內容，凸顯本質

有這樣一道找規律填數題：

用左邊的“十”字框在表中框出5個數，先算算這5個數的和，再想想算出的和與中間這個數有什么關系。如果5個數的和為105，請在“十”字框中寫出這5個數（如圖2）。

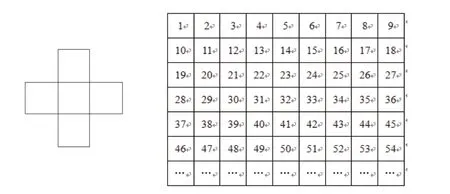
圖2

初次教學該內容時，分兩步走——

第一步，舉例→發現規律。引導學生用“十”字框任意框選一組數，通過幾組數的計算反饋，組織交流時發現“十”字框中五個數的和總是中間那個數的5倍，并且未發現任何反例。因此，如果5個數的和為105，則可以用105÷5求出中間的數為21，繼而從表中可以找出另外四個數分別是20、22、12、30。

第二步，鞏固→初步建模。在學生初步發現規律后，給出了兩道模仿練習題：如果5個數的和為120，這5個數分別是多少？如果5個數的和為65呢？由于這兩題的答案都可以從表中找到，此時的鞏固還未對學生的思維形成挑戰。事實上，絕大部分學生都是先用總和除以5求出中間的數之后，再到表中去框出其他四個數的。于是出示如下的題：如果框出的5個數的和是375呢？你還能在“十”字框中填出這5個數嗎？該題的答案是無法直接從表中簡單找到的，此時學生不得不丟開表格，進一步探究“十”字框中5個數之間的本質關系。通過深入探究和思考，他們發現“十”字框中橫向排列的三個數每兩數之間相差1，而縱向排列的三個數每兩數之間相差9。至此，5個數的相互關系基本理清。

然而，當學生在家庭作業中遇到下題時（如圖3），卻有75%的學生出現了錯誤，他們在“十”字框中是這樣填寫的：

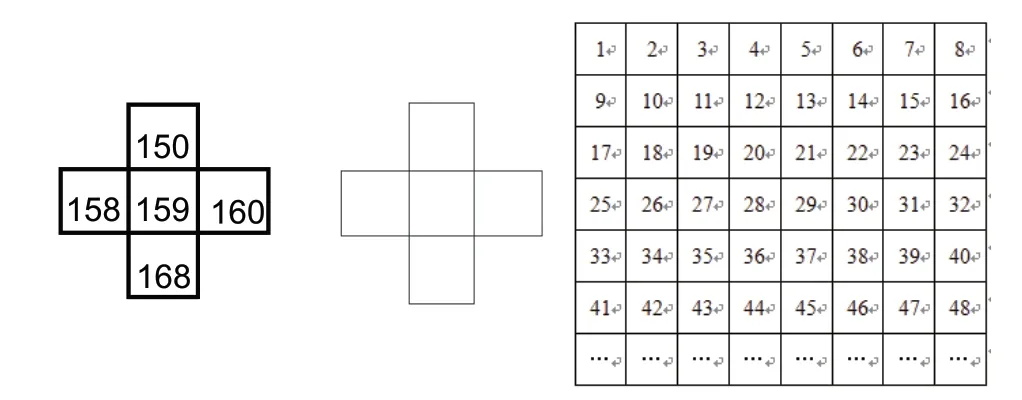
圖3

用左邊的“十”字框在表中框出5個數，先算算這5個數的和，再想想算出的和與中間一個數有什么關系。如果5個數的和為795，你能在左邊的“十”字框中寫出這5個數嗎？

換了一個數表就頻頻出錯，意味著學生對規律的認識不深刻，一旦情境發生變化，遷移便無法順利完成。能否將知識遷移到新的情境中去，是 “理解” 是否真正達成的表征。基于“理解”來思考本題的教學，又該如何來設計呢？

在原有的兩個環節基礎上再增加兩個環節：

第三步：變式→凸顯本質。出示家庭作業中的那道題，引導學生發現，每行9個數變為每行8個數后，上下兩行間相對應的兩個數的差也隨之發生了改變，因此，“十”字框中的5個數不僅會隨著中間那個數的變動而變動，也會隨著數表中數的排列特征而改變。

第四步：理解→遷移應用。再次聚焦問題，追問：從前面的兩例中我們發現，“十”字框中縱向排列的三個數之間的關系會隨著每行數的個數的變化而變化，而橫向排列的三個數每兩數之間的差卻都是1，那么，橫向排列的數差只能是1嗎？你能自己設計一個數表，給大家提供一個繼續深入探究的素材嗎？

增加的環節三通過聚焦問題、反饋、診斷性評價等，把學生的潛在誤解揭示出來，“逼”著他們提前暴露出認知上的問題。環節四則幫助學生揭示了他們的問題、疑問、假設，引導他們深入地探究該題基本框架之外的未知領域，逼近所研究問題的本質屬性，從而幫助學生搭建起從“發現”到“遷移”的“腳手架”，賦予他們一種高階思維，提高他們在靈活變化中解決實際問題的能力。