無抗沖切鋼筋的RC板柱節點受沖切承載力計算

夏成亮，史慶軒，王 震

(1.結構工程與抗震教育部重點實驗室(西安建筑科技大學)，西安 710055；2.西安建筑科技大學 土木工程學院，西安 710055)

板柱結構是一種以板和柱作為主要承重構件的結構體系，又稱為無梁樓蓋結構體系。該結構具有空間布置靈活，傳力路徑明確，結構層高較低，施工速度快等特點。以往的研究表明，板柱結構具有相對較低的抗彎剛度，在節點區域容易發生沖切破壞。由于在沖切破壞前板柱節點處于復雜的三維受力狀態，剪力傳遞機制不明確，國內外對板柱節點沖切破壞的機理一直沒有得出統一的結論，板柱節點的受沖切承載力計算方法大多都是基于簡支板沖切試驗提出的經驗公式。

為完善無抗沖切鋼筋的RC板柱節點的受沖切承載力計算方法，國內外學者進行了大量試驗研究及理論分析。文獻[1]對高強混凝土板柱節點的試驗研究表明混凝土強度與節點受沖切承載力存在非線性關系。文獻[2]考慮混凝土強度、鋼筋的銷栓作用影響對錐殼模型進行修正，通過對節點脫離扇形體建立平衡條件，推導了無抗沖切鋼筋的RC板柱節點受沖切承載力計算式。文獻[3]通過試驗證明沖切破壞是節點區塑性轉動使臨界裂縫寬度增加導致，考慮截面高度，縱筋配筋率，骨料粒徑、沖跨比等影響因素，推導出基于臨界斜裂縫理論的無抗沖切鋼筋的RC板柱節點受沖切承載力計算式。

本文認為板柱節點沖切破壞是由于板上部剪壓區混凝土受壓破壞和臨界斜裂縫區域鋼筋混凝土剪切失效共同導致。剪壓區是臨界斜裂縫未穿過的區域，其抗剪承載力由混凝土的抗壓強度提供。臨界斜裂縫區域的抗剪貢獻則由混凝土間的骨料咬合力以及鋼筋的銷栓作用提供。本文使用修正壓力場理論(MCFT)[4]計算無抗沖切鋼筋的RC板柱節點臨界斜裂縫區域的抗剪承載力，剪壓區混凝土的抗剪承載力則在確定的剪壓區范圍內建立其計算表達式。通過對板柱節點沖切試驗結果的驗算,驗證了本計算方法的正確性，為板柱節點受沖切承載力的計算提供理論依據。

1 沖切破壞機理及破壞模型

對以往無抗沖切鋼筋的RC板柱節點沖切試驗的破壞面觀察發現，在板和柱相交的位置存在混凝土局部壓碎的情況。因此本文認為無抗沖切鋼筋的RC板柱節點沖切破壞類似于梁剪壓破壞，臨界斜裂縫發展到一定程度后，將被剪壓區混凝土阻斷，存在明顯的受壓區與受拉區。由于板柱節點沖切破壞屬于三維剪切破壞，假定沖切荷載由剪壓區未開裂混凝土和臨界斜裂縫區域(包括斜拉區和受拉區)的骨料咬合力及銷栓作用共同承擔。

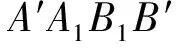
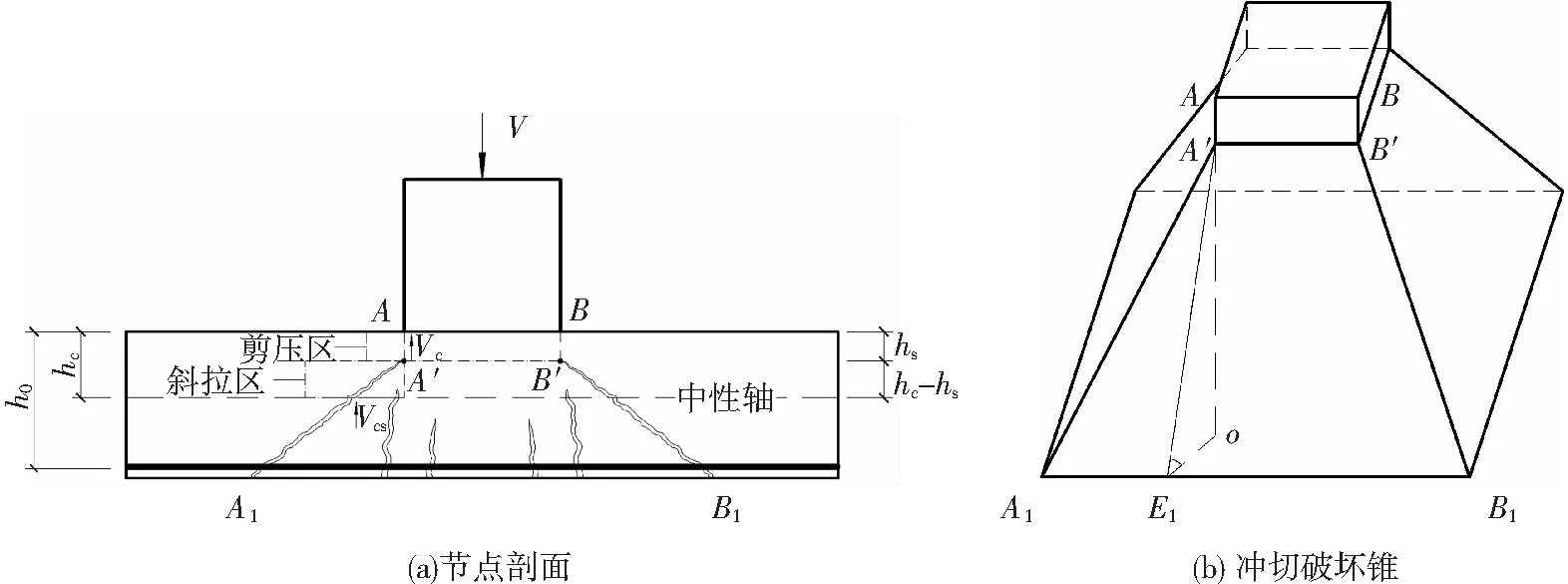
圖1 沖切破壞模型

無抗沖切鋼筋的RC板柱節點的極限沖切承載力由受壓區的承載力垂直分量和臨界斜裂縫區域骨料咬合力組成：

Vu=Vc+Vcs

(1)

本文中剪壓區混凝土提供的抗剪承載力Vc由文獻[5]提出的分析方法建立計算表達式。臨界斜裂縫區域混凝土提供的抗剪承載力Vcs基于修正壓力場理論(MCFT)，不考慮抗彎鋼筋的銷栓力，通過迭代計算得到。

2 剪壓區混凝土受沖切承載力計算

參考文獻[5]研究梁剪切失效的方法，本文將節點區分割成臨界斜裂縫隔離體I和與柱面接觸的棱柱體II，不考慮柱面對直接接觸的棱柱體II的影響，分別建立隔離體平衡條件，如圖2所示，得到剪壓區高度表達式：

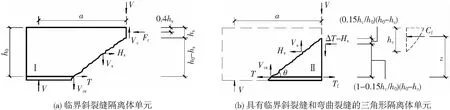
圖2 作用在節點單元上的力

(2)

式中：hs為剪壓區高度，hc為受壓區高度，h0為板有效高度，θ為臨界斜裂縫傾角。

受壓區高度由下式確定，取正根[5]：

(3)

式中：f′c為混凝土圓柱體抗壓強度，ρ為板受彎鋼筋配筋率。

在極限狀態下，假定受壓區混凝土壓應力σz符合拋物線分布規律且應變分布為倒三角形，并且壓應力σz在混凝土受壓區最外邊緣處達到混凝土抗壓強度f′c，則從受拉鋼筋中心至中性軸z處的混凝土縱向正應力σz可按式(4)計算[6]：

(4)

在剪壓區高度hs范圍內對混凝土壓應力σz積分，得到剪壓區混凝土的受剪承載力Vc貢獻表達式：

(5)

式中c為柱截面尺寸。

3 修正壓力場理論(MCFT)

修正壓力場理論(MCFT)[4]是由加拿大學者Vecchio和Collins采用非線性混凝土本構，通過對開裂混凝土單元建立平衡方程和相容方程，提出的一種計算正交雙向承受薄膜應力的鋼筋混凝土平面單元受剪承載力的方法。隨著荷載持續增大，節點區形成臨界斜裂縫并發展到受壓區，在裂縫處正應力與剪應力的共同作用下節點發生沖切破壞。本文在修正壓力場理論的基礎上推導無抗沖切鋼筋的RC板柱節點臨界斜裂縫區域的受沖切承載力。

3.1 MCFT應變協調條件

根據修正壓力場理論(MCFT)[4]中鋼筋與混凝土完全黏結的假定及應變莫爾圓理論，可得到開裂混凝土單元的應變協調條件：

εx=εcx=εsx

(6)

εy=εcy=εsy

(7)

εx+εy=ε1+ε2

(8)

(9)

式中：ε1、ε2分別為垂直于裂縫的平均主拉應變和平均主壓應變，εx、εy分別為平均橫向應變和平均縱向應變，εcx、εcy分別為混凝土橫向應變和縱向應變，εsx、εsy為分別為橫向鋼筋應變和縱向鋼筋應變。

3.2 MCFT平衡條件

將修正壓力場理論(MCFT)[4]中的鋼筋單元和開裂混凝土單元疊加得到圖3(a)所示的開裂鋼筋混凝土單元的應力狀態。根據圖3(a)所示的開裂鋼筋混凝土單元的應力狀態和圖3(b)所示的混凝土平均應力莫爾圓，可得到平衡條件：

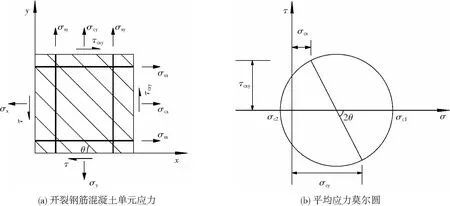
圖3 開裂鋼筋混凝土應力狀態與混凝土平均應力莫爾圓

τ=τcxy

(10)

σcx=σc1-τcxy/tanθ

(11)

σcy=σc1-τcxytanθ

(12)

σc2=σc1-τcxy(tanθ+cotθ)

(13)

式中：σc1、σc2分別為開裂混凝土的主拉應力和主壓應力，σcx、σcy分別為混凝土在x和y方向上的平均應力，τ為開裂鋼筋混凝土單元的剪應力，τcxy為開裂混凝土單元的平均剪應力。

修正壓力場理論(MCFT)[4]認為裂縫引起的局部應力對開裂混凝土單元的極限承載力有重要影響。考慮裂縫之間的局部應力可得到混凝土單元在裂縫處及裂縫間的平衡方程：

σsxcr=(σc1+τcicotθ+σsx)ρsx

(14)

σsycr=(σc1-τcitanθ+σsy)ρsy

(15)

式中：τci為裂縫表面的剪應力，σsxcr、σsycr分別為裂縫處的橫向鋼筋和縱向鋼筋的應力，σsx、σsy分別為裂縫間橫向鋼筋和縱向鋼筋的平均拉應力，ρsx、ρsy分別為橫向鋼筋和縱向鋼筋的配筋率。

3.3 開裂混凝土本構關系

3.3.1 混凝土本構

由于在拉-壓雙軸應力狀態下的混凝土比標準圓柱體混凝土強度更低、更脆，因此修正壓力場理論(MCFT)[4]采用考慮混凝土軟化現象的混凝土受壓應力-應變關系：

(16)

(17)

受拉應力-應變關系為：

當ε1≤εcr時：

σc1=Ecε1

(18)

當ε1>εcr時：

(19)

式中：Ec為混凝土彈性模量，ε′c為混凝土峰值壓應變，εcr為混凝土開裂應變，fc2max為混凝土受壓方向上的極限壓應力。

3.3.2 鋼筋本構

修正壓力場理論(MCFT)[4]假定鋼筋軸向應力僅取決于軸向應變參數，并假定垂直于鋼筋截面的剪應力為零，其應力-應變關系采用理想彈塑性模型：

σsx=Esεsx≤fsy

(20)

式中：Es為板內縱筋彈性模量，εsx為鋼筋應變，fsy為板內縱筋屈服強度。

4 無抗沖切鋼筋RC板沖切承載力計算

4.1 計算方法與步驟

修正壓力場理論(MCFT)[4]假定混凝土開裂后拉應力仍參與抗剪，由圖4所示的無抗沖切鋼筋的RC板開裂后的內力平衡可知，在兩條裂縫間的混凝土拉應力達到最大值。選取臨界斜裂縫與豎向平面截取的棱柱體作為分析對象，棱柱體應力分布與開裂RC板相同，通過對柱面與棱柱體相互接觸的平面上的應力積分來計算板的極限承載力。假定柱面與棱柱體相互接觸的平面上的剪應力均勻分布，則單塊棱柱體的沖切破壞截面的剪應力τ為：

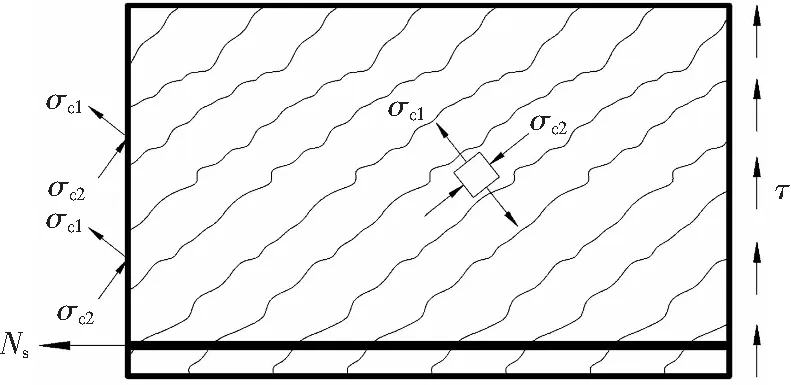
圖4 受剪混凝土的主應力

(21)

式中：h為板厚，Vcs1為單塊棱柱體承受的剪力。

通過建立棱柱體在水平方向上的力的平衡條件可得:

εx=(σc2cos2θ-σc1sin2θ)/(ρsxEs)

(22)

根據修正壓力場理論，當板未布置抗沖切鋼筋時,裂縫處的平均應力平衡關系見圖5(a)，臨界斜裂縫上存在鋼筋拉應力σsx和混凝土主拉應力σc1；兩條裂縫間的應力平衡關系見圖5(b)，存在局部剪應力τci和局部壓應力σci，其中局部壓應力σci很小，可以忽略不計。在給定外力作用下，這兩組應力狀態應該是應力等效的。因此可得到：

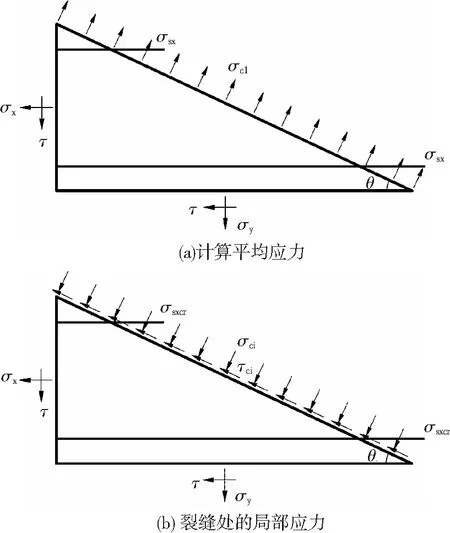
圖5 計算平均應力與裂縫處的局部應力

σc1sinθ+ρsxσsxsinθ=ρsxσsxcrsinθ-τcicosθ

(23)

σc1cosθ=τcisinθ

(24)

由式(23)可得，未配置抗沖切鋼筋的RC板柱節點沖切破壞時的最大主拉應力:

σc1max=τcitanθ

(25)

對于無抗沖切鋼筋的RC板柱節點，聯立式(10)、式(12)和式(25)可得:

τ=τci

(26)

基于文獻[4]對混凝土裂縫截面骨料咬合力的研究，當局部壓應力σci很小時，可得到局部剪應力表達式:

(27)

式中：ag為混凝土材料的最大骨料粒徑，ag通常可取為20 mm，w為鋼筋混凝土開裂單元的平均裂縫寬度，當不配置抗沖切鋼筋時，可由下式計算:

(28)

式中：Smx為垂直于x方向的裂縫間距，當鋼筋混凝土板在板頂、板底布置雙層鋼筋網時，Smx為抗彎鋼筋在垂直方向上的間距；根據文獻[7]的研究，Smx可近似取0.9h0。

臨界斜裂縫傾角θ是確定沖切錐幾何形狀和沖切承載力的重要參數，文獻[8]通過線性擬合得到了傾角θ與抗彎鋼筋配筋特征值ρsfy/fc的相關性表達式。本文通過對以往試驗數據的統計分析，發現傾角θ和柱截面周長與板有效厚度之比Cc/h0及ρsfy/fc顯著相關。因此，本文認為影響節點臨界斜裂縫傾角θ的因素主要為Cc/h0和ρsfy/fc，假定θ由以下方程式表達：

θ=a(Cc/h0)α(ρsfy/fc)β

(29)

為了確定待定系數α和β，采用文獻[9]中的分析方法，分別檢驗單一變量對臨界斜裂縫傾角θ的影響，可以得到單一變量影響系數(α和β)變化過程中對臨界斜裂縫傾角平均偏差ē的變化規律，如圖6所示。由圖可知，α和β與臨界斜裂縫傾角平均偏差ē呈明顯非線性關系，存在某一極值點使ē達到最小值。由分析結果確定待定系數后，可得到傾角θ的最終表達式：

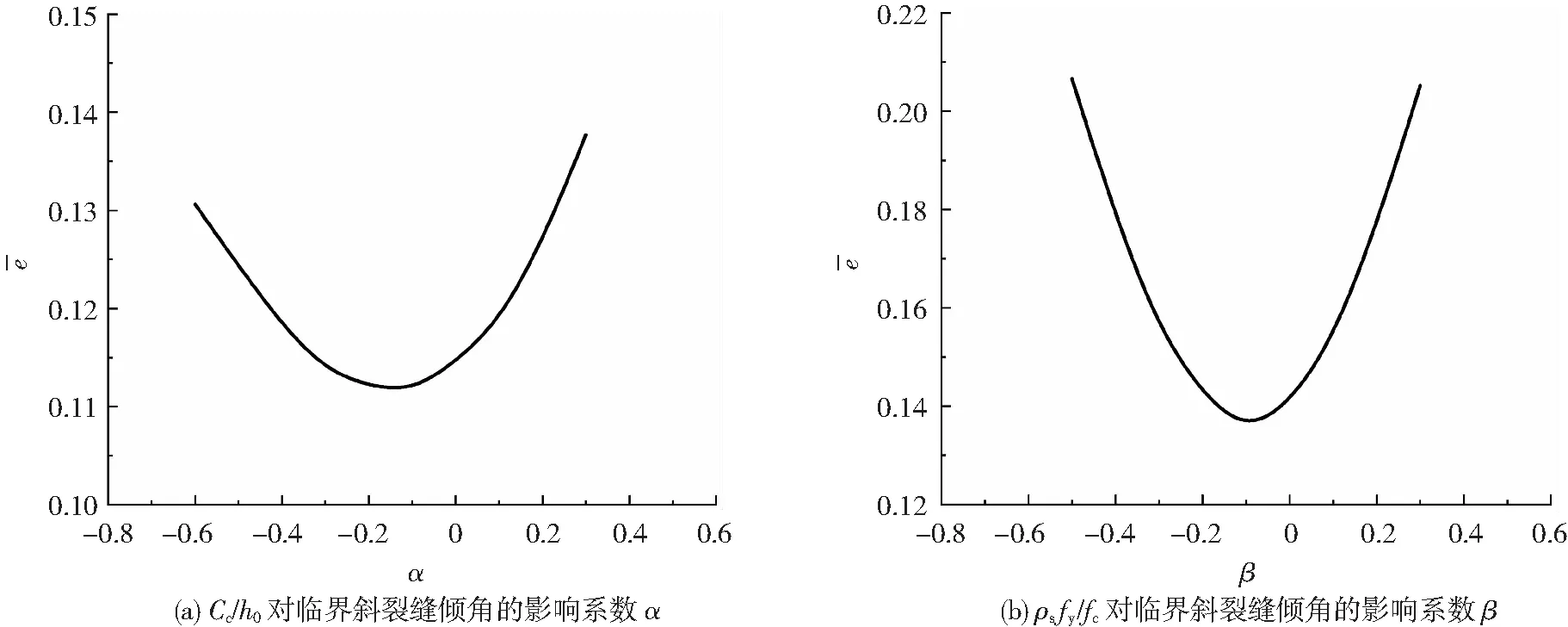
圖6 樣本平均偏差-影響因數曲線

θ=32(Cc/h0)-0.12(ρsfy/fc)-0.08

(30)

將上述公式計算的傾角與試驗值對比，本文擬合公式均值為1.09，變異系數為0.20；文獻[8]擬合公式均值為1.13，變異系數為0.20。通過表1中試驗值與計算值對比可知，本文擬合的公式不受文獻[8]中35°上限角的限制，且對除方形柱以外的其他柱截面形狀的節點預測結果較好。因此，本文擬合的角度計算公式能較好預測沖切斜裂縫傾角。

表1 沖切裂縫傾角試驗值與計算值對比

由式(20)、(26)、(27)可得，無抗沖切鋼筋的RC板柱節點在x方向上的抗沖切承載力為

[2c+2(h-hs)cotθ](h-hs)

(31)

將式(5)和式(31)代入式(1)得到節點抗沖切承載力

[2c+2(h-hs)cotθ](h-hs)

(32)

節點受沖切承載力計算流程見圖7。

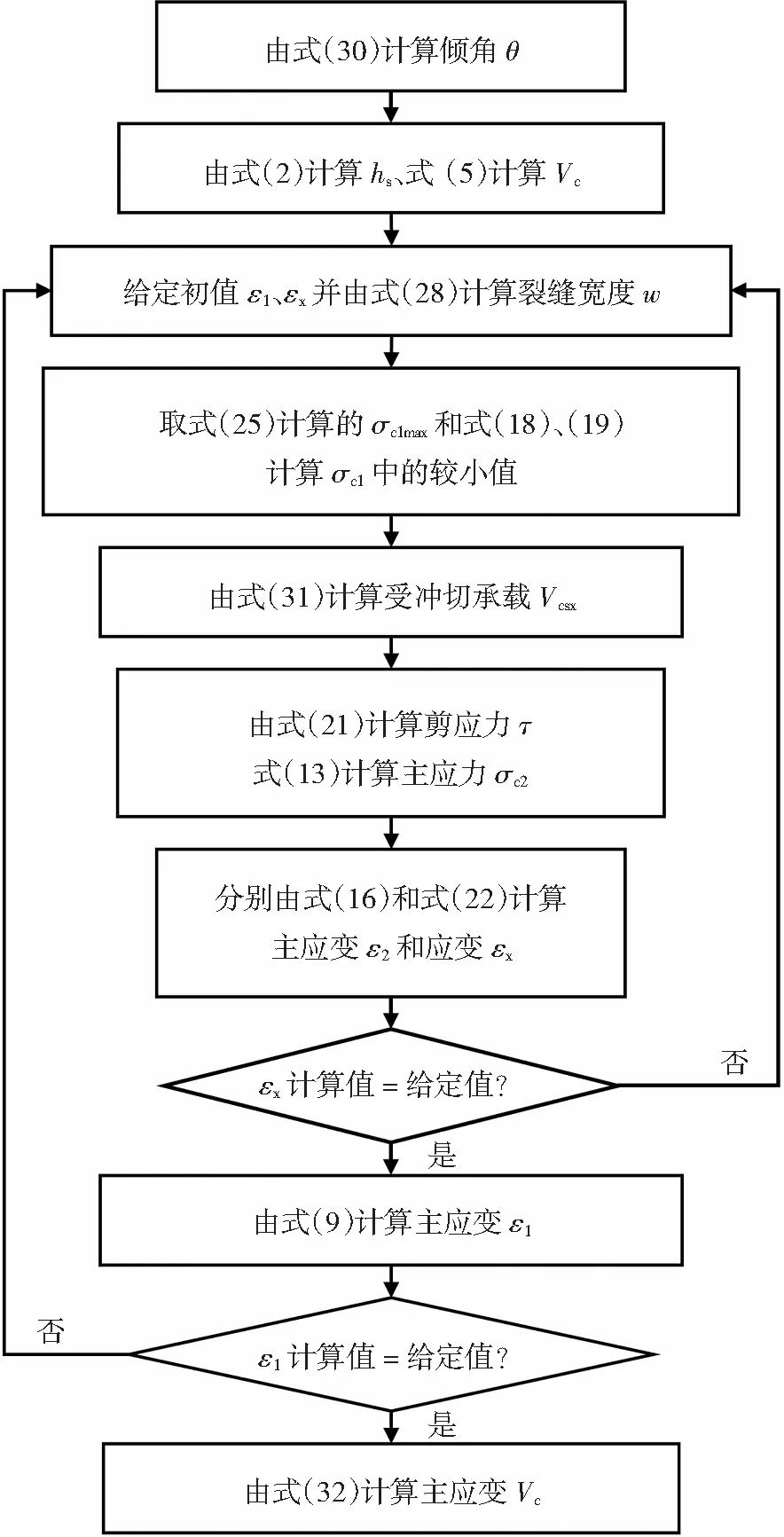
圖7 節點受沖切承載力計算流程

4.2 計算結果與試驗值對比

為驗證本文提出的沖切承載力計算方法的準確性與適用性，采用式(32)對相關文獻中54個[1-2,8,10-21]無抗沖切鋼筋的RC板柱節點在豎向荷載作用下的抗沖切試驗結果進行驗算。節點試驗的混凝土立方體抗壓強度變化范圍為27.5～124.87 MPa，柱截面尺寸變化范圍為130～520 mm, 沖跨比λ變化范圍為2.83～7.13，縱筋配筋率ρs變化范圍為0.33%～1.73%，節點支承方式均為板四邊簡支，收集的試驗數據具有一定的代表性。圖8(a)為文獻[21]的理論公式計算結果與試驗值對比。圖8(b)為本文公式(32)的計算結果與試驗值對比。由圖可知，文獻[21]的計算值與試驗值比值的平均值、標準差、變異系數分別為0.771、0.147、0.191；本文提出的計算方法的計算值與試驗值比值的平均值、標準差、變異系數分別為1.005、0.163、0.162。通過對比可知，采用本文提出的方法計算出的節點抗沖切承載力與試驗值較為接近，并且具有較小的標準差和變異系數，表明本文提出的無抗沖切鋼筋的RC板柱節點沖切承載力計算方法較為合理。

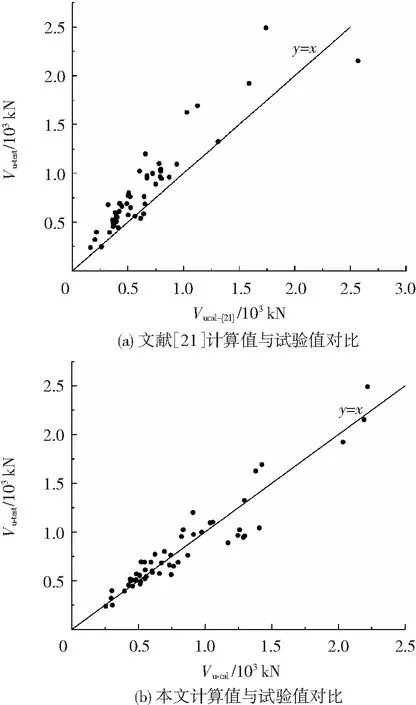
圖8 計算值與試驗值對比

5 結 論

1)本文通過對大量板柱節點沖切裂縫傾角試驗數據的總結，對影響沖切裂縫傾角的因素進行統計分析，得到臨界斜裂縫傾角θ和柱截面周長與板有效厚度之比Cc/h0及抗彎鋼筋配筋率特征值ρsfy/fc之間的相關性表達式。通過對文獻中沖切斜裂縫傾角的驗算，證明該關系式能較準確的預測無抗沖切鋼筋的RC板柱節點的沖切斜裂縫傾角。

2)將無抗沖切鋼筋的RC板柱節點的沖切破壞模式類比梁的剪壓破壞，結合修正壓力場理論(MCFT)，分析板柱節點剪壓區與臨界斜裂縫區域(包括斜拉區和受拉區)不同的受力狀態，推導無抗沖切鋼筋的RC板柱節點的受沖切承載力計算式，分別計算剪壓區與臨界斜裂縫區域的沖切承載力貢獻。通過對文獻中大量試驗結果的驗算，以及與文獻中沖切承載力計算值的比較，驗證了本文提出的計算方法的準確性及適用性。