基于圓形塊匹配的無人機航向角解算算法*

李天松， 張浩強， 楊溢凡， 連 濤

(桂林電子科技大學 信息與通信學院, 廣西 桂林 541000)

0 引 言

無人機(unmanned aerial vehicle,UAV)由于其成本低、功耗低、靈活性高等優點已經越來越多地應用于生產生活當中。由于捷聯式慣性導航技術的快速發展與微機電系統(MEMS)慣性器件的日趨成熟，無人機的實時姿態解算與控制問題已經成功解決。但是，使用傳統的六軸傳感器，只能將加速度計與陀螺儀所得數據進行卡爾曼濾波[1]或者互補濾波[2]來修正橫滾角與俯仰角，無法對無人機的航向角漂移進行補償修正，航向角精度會隨著時間的增長而不斷降低[3]。目前，比較常用的航向角檢測方法是使用地磁檢測傳感器，這種方式有效解決了航向角漂移問題，但地球磁場是極其微弱的，無人機的地磁傳感器又工作在復雜電流、電機旋轉等因素引起的電磁場復雜的環境中，極易對地磁傳感器的檢測造成干擾。目前，視覺運動感知系統，即光流傳感器已經成功應用于無人機的懸停定點[4]。光流是由相機和場景相對運動產生的，光流場是指圖像灰度模式的表面運動。Horn和Schunck在灰度圖像分析中引入了二維速度場的概念[5]，并建立了光流基本約束方程，為早期的光流計算發展起到了奠基性作用。由Lucas與Kanade發明的Lucas-Kanade算法[6]可以計算出連續拍攝序列圖像序列上的光流信息，得到了廣泛的應用。

塊匹配算法是最通用的光流計算方法，本文將塊匹配光流算法進行了改進，通過圓形塊匹配方式改善了匹配效果，并將其應用于無人機的航向角檢測。經過對連續的拍攝畫面進行逐幀檢測，證明該方法可以準確地解算出無人機的航向角，并且相較于陀螺儀有效抑制了漂移，相較磁力計沒有電磁干擾帶來的影響。

1 塊匹配光流算法原理

1.1 匹配過程

在攝像頭與被拍攝物體存在相對運動時，所拍攝的不同幀之間會有邊界遮擋的現象，所以難以檢測整幅圖像的運動狀態。而且，在連續的視頻中檢測全局圖像運動情況會有極大的運算量。在此情況下提出了塊匹配光流算法。塊匹配技術的前提是：所拍攝的畫面在運動量很小、時間間隔很小的情況下默認兩幅圖像中物體在畫面中所呈現的灰度沒有引起變化；在足夠小的區域內，物體的運動情況是相同的[7]。在此前提下，將視頻圖像序列分為很多不重疊的小塊，假設塊內的所有像素點的運動狀態相同，且只發生平移運動，然后在目標圖像中按照一定的匹配準則、通過一定的搜索算法尋找與此小塊最相似的塊，計算出該小塊在目標圖像中相對位置的變化即為運動矢量。如圖1所示。

圖1 塊匹配光流法示意

圖1為第k-1幀圖像與k第幀圖像進行匹配的示意圖。圖1中M，N分別為所設置匹配塊的長和寬，一般取M與N相等。這里，當M與N的取值過大時，則上述塊內所有像素運動狀態相同的前提條件就會不成立，而M與N的取值過小會使塊內包含的信息量過小導致匹配精度下降。在目前的H.26x與MPEG[8]等視頻壓縮標準中，均按式(1)取

M=N=16

(1)

這個取值已經被實踐證明過能取得較好的匹配效果。um與vm為匹配塊的最大橫向位移與縱向位移，則長寬分別為M+2um,N+2vm的矩形區域則為在第k幀圖像中搜索范圍的大小。經過一定的搜索算法得到最佳匹配塊，則向量w為匹配塊在k-1幀到k幀間的運動矢量。

1.2 匹配準則

光流的塊匹配準則主要有均方差準則(MSE)、歸一化相關函數(NCCF)、平均絕對誤差準則(MAD)、絕對誤差和準則(SAD)等。其中,MAD與SAD容易實現，是比較常用的兩種匹配準則，這里對其進行介紹。

平均絕對誤差準則是指待匹配塊與搜索塊對應像素點灰度值之差的絕對值的平均值

(2)

式中M與N為所選取塊的長寬，fk與fk-1為第k幀與第k-1幀的像素點灰度值，(i,j)為像素點在匹配塊中的坐標，u與v為搜索塊相對于待匹配塊的橫向與縱向位置偏移。當MAD最小時，則認為向量(u,v)為第k-1幀待匹配塊在第k幀的運動位移。由于平均絕對誤差準則不需要進行平方運算，運算的復雜度較低，所以經常被使用。

為了進一步降低運算的時間復雜度與空間復雜度，提出了絕對誤差和準則。由于M與N的值在匹配過程中是確定的，所以,對上述所得的像素灰度絕對值不取平均值則為絕對誤差和準則

(3)

同樣的，當SAD最小時，向量 (u,v)為第k-1幀待匹配塊在第k幀的運動位移。

2 圓形塊匹配法

2.1 方形匹配塊存在的問題

現有的塊匹配光流算法中，選取16×16的正方形匹配塊，并且默認匹配塊只做平移運動而沒有旋轉、縮放等運動。但是，搭載光流傳感器的設備尤其是無人機，做航向調整、拉升及降落是常用到的動作。例如，飛機在旋轉速度很快時，相鄰的兩幀圖像就會有過大的相對旋轉角度，后面一幀搜索到的匹配塊與待匹配塊的相似性就會大打折扣。圖2(a)為在某圖片中選取的16×16的方形待匹配塊灰度的平面分布圖，圖2(b)為此圖片旋轉過一定角度后對待匹配塊進行匹配所得塊的灰度平面分布圖。

圖2 正方形塊灰度平面分布

如圖2所示，匹配結果灰度值分布中，“黑影”部分相對于整塊的位置相較待匹配塊“黑影”部分相對于整塊的位置有了一定的變化。由于圖像轉過了一定的角度，而匹配塊依然使用相對于原圖像沒有旋轉的正方形塊，所以導致了匹配質量一定程度的下降。

2.2 圓形匹配塊匹配法

由2.1節知，方形匹配塊在圖像發生旋轉時會有一定的缺陷。由此本文提出一種新的匹配塊：圓形匹配塊。圓形是沒有方向的，所以如果使用圓形塊作為匹配塊，即使圖形發生旋轉，理論上也可以準確地得到匹配結果。圓形匹配塊的生成如圖3所示。

圖3 圓形匹配塊的生成

邊長為16，具有256個像素點的方形匹配塊已經被證明具有較好的匹配效果，所以，此圓形匹配塊依然保留256個像素點。以9個像素點的長度為半徑畫圓，圓的邊界處大于1/2的像素點保留，小于1/2的像素點去掉，得到的匹配塊即為包含256個像素點的圓形匹配塊。

圖4(a)為與圖2(a)同一位置選取的圓形待匹配塊灰度的二維分布圖，圖4(b)為在圖像旋轉過后對圓形待匹配塊匹配所得塊的灰度二維分布，圖4(c)為將匹配所得塊逆時針旋轉一定角度所得塊的灰度二維分布圖。

圖4 圓形匹配塊灰度分布

如4圖(a),(b)所示，在相鄰兩幀圖像旋轉過一定角度后，匹配所得塊中的“黑影”確實發生了旋轉，但由于圓形匹配塊的方向性表現不強，如圖4(c)將匹配所得塊再逆時針旋轉一定角度后，依然可以得到與待匹配塊較相似的塊。

設圓形匹配塊偏移矩陣為block，偏移矩陣block為256行2列的矩陣，每一行為以18×18方塊左上角像素點為起點的偏移坐標。用block(i)表示block矩陣中第i行所表示的坐標，則

(4)

式中L為圓形匹配塊包含的像素點數，即L=256。同樣的，當SAD最小時，(u+v)為當前匹配塊的位移向量。

2.3 圓形塊匹配光流算法實驗

為了檢驗用圓形匹配塊的匹配效果，分別用傳統的方形塊匹配與圓形塊匹配光流算法檢測如圖5兩幅畫面的光流情況，其中圖5(b)圖像相對于圖5(a)發生了一定角度的旋轉，兩幅均為同一相機采集的像素為300×400 的圖像。為了方便展示與計算快捷，均采用稀疏光流檢測[9]，且為了消除光流檢測的邊界遮擋帶來的影響，只取圖像中心位置7×7的方陣，共49塊匹配塊來進行匹配，且兩次檢測的匹配塊偏移的起點均相同。

圖5 光流檢測圖片樣例

首先采用方形匹配塊進行匹配檢測，匹配效果如圖6(a)，然后采用圓形匹配塊進行匹配檢測，匹配效果如圖6(b)。在圖6(a)與圖6(b)中，用白色的線條表示所檢測到的匹配塊的位移向量。觀察圖6(a)與圖6(b)可以發現，在圖像發生一定角度旋轉后，采用正方形匹配塊檢測得出的光流信息已經發生了失真的情況，而采用圓形匹配塊檢測的光流信息則沒有出現失真情況。在這里，提出用兩次檢測所有匹配塊匹配的SAD值之差來定量比較匹配效果

圖6 光流檢測效果

(5)

式中SADD為兩次檢測所有匹配SAD之差，SAD(i)為對第i塊圓形匹配塊進行檢測的SAD值，SAD2(j)為對第j塊方形匹配塊進行檢測的SAD值，p為選取的匹配塊個數，即p=49。

由于SAD值越小，認為搜索到的匹配塊與待匹配塊越相似，那么可以得出當SADD值小于0時，則可以認為圓形匹配塊的匹配效果總體上優于方形匹配塊的匹配效果，對以上兩次檢測計算SADD，得出結果為-1 120。

光流檢測經常是一個連續的過程，接下來連續的畫面進行基于圓形匹配塊與方形匹配塊的光流檢測，對比其檢測效果。截取分辨率為300×400 的30幀的視頻進行連續的光流檢測，并對兩次檢測逐幀計算 ，得出結果如圖7所示。

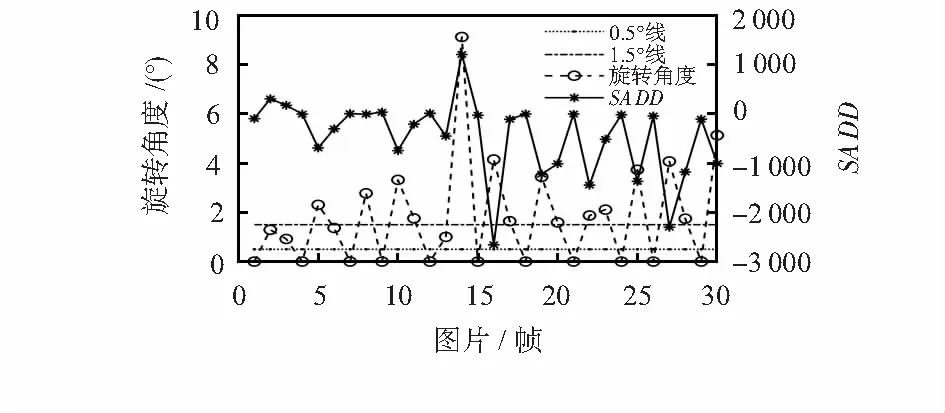
圖7 連續光流檢測SADD對比

如圖7，實線表示兩次檢測的SADD值，虛線表示圖像旋轉過的角度。圖7顯示：有73.3%的SADD檢測結果小于0；關鍵的，那些大于0的SADD值除去個別點外幾乎都處于0的附近，此時對應的旋轉角度也幾乎為0；旋轉角度超過0.5°的19個點中有16個點的SADD小于0，占84.2%；旋轉超過1.5°的15個點中，有14個點的SADD小于0，占93.3 %。因此可以得出結論，當畫面發生一定旋轉時，圓形匹配塊的匹配效果總體上優于方形匹配塊的匹配效果。

3 基于圓形塊匹配的航向角檢測

3.1 光流航向角檢測算法

通過第2章得出結論，由于圓形匹配塊的方向性較弱，當圖像發生旋轉時，圓形塊的匹配效果優于方形塊，所以本小節針對搭載光流傳感器的無人機，提出基于圓形塊匹配的航向角檢測算法。

首先，如圖8(a)所示，以原圖像第一個像素點為原點，水平像素點方向為x軸，豎直像素點方向為y軸，在原圖像中選取兩塊相距一定距離的圓形待匹配塊A和待匹配塊B，在原圖像中的坐標分別為(xa0,ya0),(xb0,yb0)計算塊A與塊B的連線與X軸的夾角α0。則有

(6)

圖8 圓形匹配塊航向角檢測示意

其次，如圖8(b)在旋轉后的圖像中搜索塊A與塊B，得到目標塊A1，B1，其坐標分別為(xa1,ya1),(xb1,yb1) ，則A1與B1的連線與x軸的夾角為α1

(7)

則搭載此光流傳感器的無人機在這一幀的航向角變化量Δyaw1為

Δyaw1=α1-α0

(8)

連續進行航向角檢測，無人機的航向角即為Δyaw的累加

(9)

將式(8)代入式(9)得

(10)

3.2 航向角檢測實驗驗證

拍攝一段對著固定物體在夾角60°內左右搖晃的視頻，截取其中5 s，視頻幀速率為28.08幀/s，幀寬度為300 P，幀高度為400 P。對此視頻的前130幀圖像逐幀進行基于圓形塊匹配的航向角檢測，輸出結果如圖9所示。

圖9 連續視頻航向角檢測結果

如圖9所示，3.1節中提出的基于圓形塊匹配的航向角解算算法可以有效地檢測出攝像頭正對的畫面旋轉情況，即無人機的航向角。

傳統的航向角檢測方法中，對于陀螺儀檢測，由于重力加速度與無人機z軸共線，所以加速度計無法修正航向角的漂移，致使檢測結果會有積分累積誤差；對于磁力計檢測，雖然可以解決漂移的問題，但由于地球磁場極其微弱，一般情況下只有微弱的0.5 Gs，而一個普通的手機喇叭當相距2 cm時仍會有大約4 Gs的磁場，所以磁力計檢測所得的航向角極易受到干擾。圖10為分別使用陀螺儀采用四元數法[10]、磁力計、圓形塊匹配光流法進行30 s的靜態檢測結果。

圖10 陀螺儀、磁力計、光流所得航向角對比

由圖10可以看出，陀螺儀積分所得的航向角在30 s產生了5°左右的漂移，磁力計數據沒有漂移但是噪聲很大。使用圓形塊匹配光流法解算所得的的航向角靜態數據既沒有產生漂移，也幾乎沒有受到干擾。因此可以得出結論，采用圓形塊匹配航向角解算算法所得的航向角靜態數據具有幾乎無漂移、不易受干擾的優點。

但是，值得提出的是：實際上上文所提出的圓形塊匹配光流航向角解算算法也是采取了累積的方法，在進行長時間動態檢測時，同樣會產生累積誤差。此外，圖像處理算法的空間與時間復雜度較高，圖像數據采集周期較長，所以，基于光流法的航向角檢測數據輸出頻率以及所需要的硬件資源遠遠高于陀螺儀與磁力計。因此，基于圓形塊匹配光流檢測所得的航向角可以用來定期修正航向角，而不可以用來直接進行姿態控制。

4 結束語

本文分析了傳統塊匹配光流算法的位置解算思路，并發現在檢測畫面發生旋轉時傳統正方形塊匹配算法存在的缺陷，在此基礎上，提出了圓形塊匹配光流算法。通過實驗計算兩次檢測所有匹配塊匹配的SAD值之差得出：圓形塊匹配算法在檢測畫面發生旋轉時相較于方形塊匹配算法有較好的檢測效果。由于圓形塊對方向的不敏感性，本文基于圓形塊匹配光流法進一步提出基于圓形塊匹配的航向角解算算法。實驗證明：此算法可以有效檢測所拍攝畫面旋轉角度的變化，并相較于陀螺儀、磁力計檢測具有靜態無漂移、不易受環境干擾的優點。