基于虛擬阻抗和模糊PID的微電網下垂控制策略*

王福忠， 李潤宇， 張 麗

(河南理工大學 電氣工程與自動化學院，河南 焦作 454000)

0 引 言

近年來，由于光伏、風電、儲能系統和燃料電池等分布式電源的快速發展，微電網的控制研究也在不斷進行[1，2]。在各等級微電網中，低壓微電網更趨向于用戶側，規模小，且多為電力或能源用戶使用。作為主要控制方式的下垂控制可以更好地去協調微網中各微源的功率輸出，且不依賴通信以及“即插即用”的特點[3～5]。在低壓微電網中線路阻抗主要呈阻性[6],通常P-V/Q-f下垂控制更加適用于低壓微電網[7,8]。但在低壓微電網中，由于線路阻抗中依然存在感性成分以及線路阻抗的不同[9]，會出現功率耦合的問題。當負荷產生波動時，P-V/Q-f下垂控制并不能進行功率的合理分配，系統的頻率和電壓也會受到影響，無法保證系統的整體穩定性。

文獻[10]提出了一種基于虛擬阻抗的改進下垂控制策略，旨在低壓微電網中引入虛擬阻抗，線路阻抗中的阻性部分發生改變，從而削弱了功率耦合以及達到無功精確分配和抑制無功環流的目的。但均需要加入很大的虛擬電感來使逆變器的輸出阻抗改變，因低壓微電網呈阻性較多，不如構造其本身的輸出阻抗，這樣更易控制。文獻[11]引入動態虛擬阻抗，使得低壓微電網下可呈現阻性，從而進行合理功率分配。但未考慮在系統產生波動時的影響，且由于下垂系數固定，很難良好地進行調節。文獻[12]提出了一種粒子群算法改進下垂系數的方法，通過改善控制參數來合理分配負荷功率，實現無差控制來保證系統的穩定。文獻[13]中將連接線路的阻抗角作為一個變量引入到下垂控制中, 并添加了一個微分控制環節，從而減小系統在暫態過程中的振蕩。但只考慮了功率的穩定性輸出問題，并未考慮到系統電壓和頻率。

對于上述問題，本文提出了基于虛擬阻抗的低壓微電網下垂控制策略，在P-V/Q-f下垂控制上引入虛擬阻抗，使系統的阻感比發生改變，使得低壓微電網呈現阻性，更好地解決功率耦合的問題。在此基礎上，又引入模糊比例—積分—微分(proportional integral differential,PID)控制器，來解決引入虛擬阻抗后以及負荷波動時，功率分配以及電壓和頻率產生波動的問題，使得P-V/Q-f下垂控制可更好適用于低壓微電網。最后通過仿真驗證此策略的合理性與有效性。

1 P-V/Q-f下垂控制

當逆變器工作在低電壓系統環境下，這時的線路阻抗特性多呈現為阻性，線路中的阻抗比為7.7[14]，并且功率角θiL也非常小，故當線路電感X忽略不計時，由此推導出的P-V/Q-f下垂控制的方程式為

(1)

但實際低壓微電網中雖然線路阻抗以阻性為主，由于不同逆變器上的線路阻抗不同，會出現功率耦合問題，所以依然不能忽略感性成分。從式(1)可以看出，P-V/Q-f下垂控制是在忽略感性的情況下得到的，所以,需要將系統的總阻抗設計為純阻性。故需引入虛擬阻抗來滿足式(1)條件，且由于下垂系數固定，在引入虛擬阻抗后,P-V/Q-f也并不能良好控制系統的功率分配以及電壓和頻率。

2 低壓微電網下垂控制策略

對于上述問題，本文提出低壓微電網下垂控制策略，總框圖如圖1所示。在引入虛擬阻抗解決系統阻感性的基礎上，加入模糊PID控制器[15，16]，代替原本的固定下垂系數，使得整個下垂控制可以進行自適應調節。

圖1 低壓微電網下垂控制的總框圖

2.1 虛擬阻抗的引入

圖2 引入虛擬阻抗后的電壓電流雙環控制框圖

在引入虛擬阻抗后，系統的等效阻抗[17]為

(2)

圖3 輸出阻抗矢量圖

從圖3中可以看出系統的輸出阻抗，在加入虛擬阻抗后，基本上呈純阻性，此時逆變器的功率可進行良好的解耦，P-V/Q-f下垂控制能夠適用于低壓微電網。

2.2 自適應模糊PID控制

在P-V/Q-f下垂控制方程式(1)的基礎上加入積分和微分環節，構成改進下垂控制方程為

(3)

式中mPi和nPi在穩態負荷中起核心作用，加快響應速度，提高系統調節精度；mIi和nIi起到消除穩態誤差的作用；mDi和nDi用來調節系統的動態性能。

但由于傳統的PID參數值也是固定的，當負荷多次變化時，可能無法對下垂控制進行精確地調節。故本文在傳統PID的基礎上加入模糊算法，使得PID參數可根據負荷變化實時進行在線調節下垂系數，構成自適應下垂系數。

對于模糊PID控制器的設計分為以下步驟：

1)模糊變量與隸屬度函數

模糊PID控制器將ep(t),ecp(t),eQ(t)和ecQ(t)作為輸入量，輸出量為KP,KI,KD。輸入、輸出量在模糊集上的論域和模糊子集[15]分別表示為

論域：輸入量和輸出量=[-3,-2,-1,0,1,2,3]

模糊子集：{NB,NM,NS,ZO,PS,PM,PB}

具體控制器參數設定為：輸入量ep(t)和ecp(t)的基本論域均為[-2 000,2 000]，量化因子為1.5×10-3；eQ(t)，ecQ(t)的基本論域均為[-3,3]，量化因子為1。輸出量KP,KI,KD的基本論域分別為[-3×10-4,3×10-4]，[-3×10-3,3×10-3]，[-6×10-7,6×10-7]量化因子為104,103,5×106。控制器輸入量和輸出量的隸屬度函數如圖4所示。

圖4 輸入和輸出的隸屬度函數

2)制定模糊規則

通過專家知識以及經驗法，采用“If e(t) is A and ec(t) is B thenKPiis C”的控制規則語句，KIi,KDi同理。通過仿真得到圖5所示的KPi,KIi,KDi的具體變化情況以及表1所示的模糊控制規則。

圖5 KPi,KIi,KDi觀測曲面

表1 模糊控制規則

3 仿真驗證與分析

本文將通過MATLAB/Simulink仿真去建立仿真模型。分別搭建P-V/Q-f下垂控制仿真和本文所提出的下垂控制策略仿真，考慮在負荷波動/投切時的情況下，對系統功率均分以及電壓和頻率變化進行對比并分析，驗證低壓微電網下垂控制策略的優勢和有效性。

此次仿真將采用兩個微源DG1和DG2作為并聯運行，由于此次仿真重點在于對逆變器的控制，故微源采用直流電源等效模型，且兩臺逆變器的容量相同。同時系統接入兩個可變負荷Load1和Load2。具體仿真參數:直流電源Vdc為800 V，濾波器電容C為1 500 μF，濾波器電感L為0.6 mH，額定有功功率Pn為20 kW，額定無功功率Qn為0 kW，虛擬阻抗Rv-jLv為(1.114 5-j0.004 85)Ω，DG1線路阻抗Z1為(0.2+j0.002 6)Ω，DG2線路阻抗Z2為(0.9+j0.117)Ω，負荷Load1為(5+j3)kW，負荷Load2為(4+j2)kW。

仿真設定：在初始時，DG1和DG2以及Load1最初投入運行，在0.3 s時Load2投入運行，0.6 s時Load1退出運行。

從圖6中可以看出，在P-V/Q-f下垂控制策略下，DG1和DG2的無功功率在0.6 s時Load1退出時有明顯突然波動，但基本達到合理分配，而有功功率沒有實現合理分配，DG1和DG2均出現了輸出偏差，這是由于線路阻抗不相同的影響。

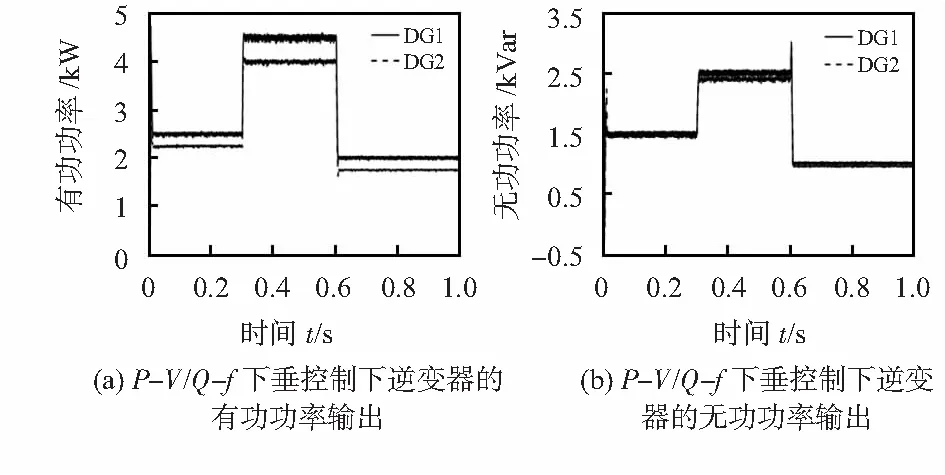
圖6 P-V/Q-f下垂控制的仿真波形

在采用本文所提出的下垂控制策略后，從圖7中可以看出，在虛擬阻抗和模糊PID的作用下DG1,DG2的有功功率各輸出4 500 W，無功功率各輸出2 500 Var，均達到了合理均分的目的。

圖7 本文所提下垂控制仿真波形

圖8將三種不同控制下的電壓進行對比，可以看出，在圖8(a)中系統的母線電壓因受到負荷投切/波動的影響，電壓在0.3 s時出現下降至375 V，穩定后一直保持，并沒有恢復至380 V，在0.6 s時，由于負荷切出，產生短暫的升高。圖8(b)中，加入PID控制后，系統電壓在0.3 s時，并沒受到負荷投入的影響，系統電壓保持在380 V，但在0.6 s還是受到了負荷切出的影響，未能良好的調節。圖8(c)中為本文所提下垂控制，能夠良好且快速地調節電壓，使得系統電壓幾乎不受負荷投切的影響，始終保持在380 V。

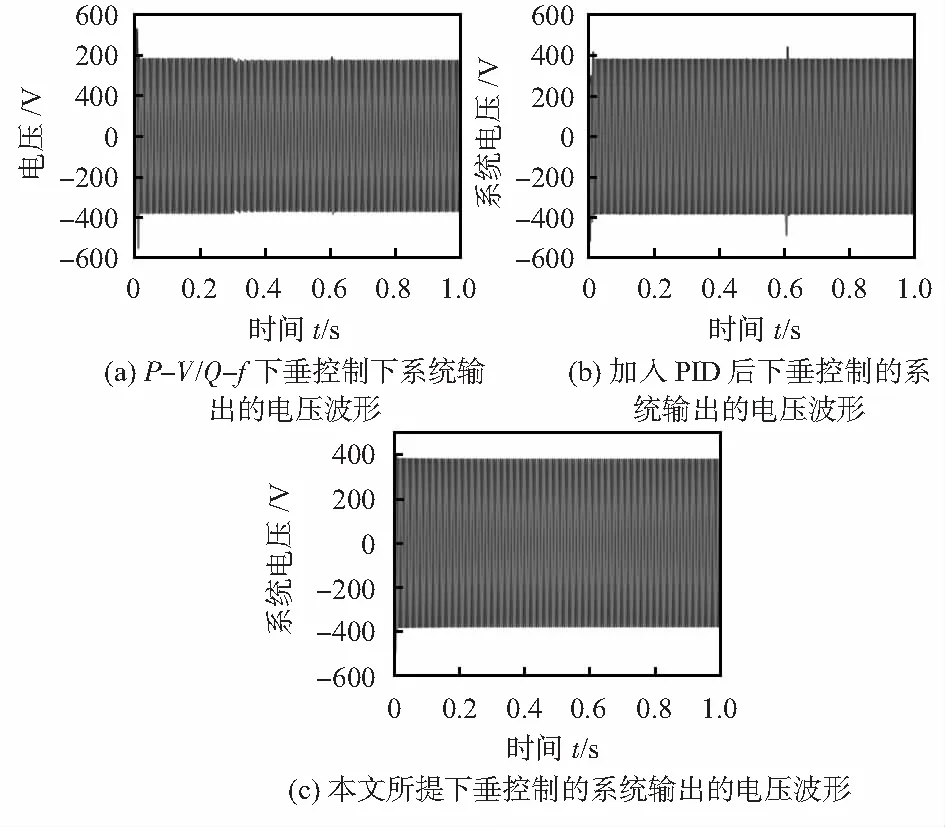
圖8 三種控制下的系統電壓對比

圖9將三種下垂控制方式下的頻率進行對比，可以看出，傳統的下垂控制在0.3 s時，由于負荷投入，頻率出現下降，降到49.97 Hz，并穩定在49.99 Hz，沒有恢復到工頻，在0.6 s負荷切出后，頻率出現上升達到50.012 Hz，并穩定在50.01 Hz，也沒有在恢復至工頻。

圖9 三種控制方式下的系統頻率對比

而在引入PID控制后，頻率在0.3 s時，下降到了49.985 Hz，在經過0.1 s后，恢復至工頻，在0.6 s時，頻率再次上升至50.01 Hz，在經過0.1s后，恢復至工頻，從分析來看，加入PID控制后，頻率的波動比傳統下垂控制要小，并能夠恢復至工頻，但由于PID調節參數固定，所以,頻率還是會因負荷的投切產生波動，且恢復至工頻時間較慢。

在本文所提方法下，由于下垂系數自適應調節，故系統頻率幾乎不受負荷波動/投切的影響，且始終保持在工頻50 Hz左右，從而保證整個系統可以更加穩定的運行。

4 結 論

P-V/Q-f下垂控制在低壓微電網中受線路阻抗和負荷波動的影響，從而無法良好地進行控制。對此，本文提出了基于虛擬阻抗的低壓微電網下垂控制策略，通過引入虛擬阻抗，來解決系統中出現的功率耦合問題以及改變線路阻抗，使得P-V/Q-f下垂控制更好地適用于低壓微電網。同時，在P-V/Q-f下垂控制的基礎上引入模糊PID，能夠自適應調節下垂系數。通過仿真對三種控制方式進行比較，證明了基于虛擬阻抗和模糊PID的微電網下垂控制策略可以有效地應用于獨立低壓微電網，提高系統中有功功率和無功功率的分配精度，并且在系統出現擾動時，很好地抑制電壓和頻率的波動，整體提高了系統的運行穩定性。