支柱沉降作用下球形儲罐的屈曲研究

黃 思，易天坤，歐晨希，林冠堂

(1.華南理工大學 機械與汽車工程學院， 廣州 510641；2.廣東省特種設備檢測研究院珠海檢測院，廣東 珠海 519002)

球形儲罐被廣泛應用于石油、化工、冶金、輕紡、城建、市政等工業領域中，主要用于儲存液態丙烷、丁烷、丙烯、丁烯及其混合物等[1]。當結構在微小擾動(載荷變化)使結構發生較大的形態變化，則稱為結構發生屈曲或失穩，通常結構屈曲的發生表現為變形的突然增大。由于受到基礎質量、安裝施工、地理環境等因素的影響[2]，很難使球罐支柱保持在同一水平面上，支柱一旦沉降，球罐受力不再均勻，球罐局部受力過大可能會屈曲或破損。

國內外學者相繼開展了儲罐在沉降下的靜力學研究和屈曲研究。靜力學研究方面，Dorazio等[3]通過實驗對圓柱儲罐在不均勻沉降下的變形和應力進行了簡單的測量；Yang等[4]采用有限元法計算了支柱不均勻沉降下的球罐應力和支柱位移；高紅利等[5-6]研究了基礎不均勻沉降對直徑為9.2 m的球罐應力的影響；房江祥[7]以1.5 m3球罐為研究對象，運用ABAQUS軟件來模擬球罐支柱沉降對其拉桿應力和極限載荷的影響。Chen等[8]通過ANSYS軟件建立了圓柱儲罐的有限元模型，研究了圓柱儲罐在不均勻沉降下的變形行為。屈曲研究方面，Jonaidi等[9-10]采用有限元和實驗驗證的方法，研究了圓柱儲罐在理想諧波沉降下的屈曲響應；Godoy等[11-12]采用實驗方法研究了局部沉降下圓柱鋼儲罐的屈曲響應；范海貴[13]采用現場實測、理論推導和有限元數值模擬相結合的方法，研究了圓柱儲罐在沉降和軸向載荷聯合作用下的屈曲響應；蘇文強[14]建立了大型圓柱儲罐在不均勻沉降和風載荷聯合作用下的屈曲數值模擬方法。

綜上所述，大多數學者已對圓柱儲罐在沉降下的靜力學和屈曲變形進行了大量的研究。但針對球罐的研究主要集中于沉降下的靜力學研究，缺乏對沉降下的球罐的屈曲變形研究。球罐支柱的沉降量達到一定程度時，球罐可能因局部受力不均而發生屈曲變形和破壞。因此，選取1臺5 000 m3的在役丙烷球罐為研究對象，對其支柱在3種不均勻沉降形式下進行屈曲響應研究，為球罐設備的管理和維護及穩定運行具有重要工程意義。

1 計算模型

研究對象為1臺5 000 m3的在役丙烷球罐，球罐的結構示意圖如圖1所示，其結構尺寸的基本參數和主要結構的材料特性參數如表1、2所示。

圖1 球罐結構示意圖

表1 丙烷球形儲罐設計參數

表2 球罐主要結構的材料特性參數

2 屈曲響應分析

2.1 網格劃分

采用Workbench平臺中的Mesh對球罐進行結構網格劃分，為避免網格單元數目對計算結果的影響，需要考察計算域在幾種不同網格數量下的計算結果。同時考慮到本文僅對球罐進行屈曲變形的研究，因此以單根支柱沉降1 mm為例，圖2給出了通過Workbench平臺計算得到的球罐的最大總位移xmax隨計算網格數的變化情況。

圖2 網格無關性檢驗曲線

由圖2可知，當球罐的網格數達到75萬之后，球罐最大總位移xmax值基本穩定。考慮到計算的精度和成本，選用767 830為球罐計算域的網格數量，模型網格劃分結果如圖3所示。

圖3 網格劃分結果示意圖

2.2 載荷與約束條件

考慮球罐充裝率φ為90%的工況[16]，該工況下，球罐的載荷有重力G、內壁承受均布的壓力p。其中壓力載荷p(Pa)隨液面高度h(m)呈線性變化，其變化規律為：

p=po+(R-h)ρlg

(1)

式中：po為球罐的工作壓力，為1.42 MPa；R為球罐的半徑；ρl為液態丙烷密度，為474.04 kg/m3；g為重力加速度，取9.81 m/s2。

圖4給出了支柱編號的示意圖，對于球罐的支柱不均勻沉降的模型，考慮了3種沉降形式：單根沉降、蝶形沉降和兩根沉降。表3給出了3種沉降方式下每根支柱的沉降量(Sd)。在設置支柱的沉降量時，通過對沉降支柱的底板設置沿著軸向向下的位移，從而實現對球罐不均勻沉降的有限元模擬。

圖4 支柱編號示意圖

表3 3種沉降方式的沉降量(Sd)

2.3 屈曲分析原理

當加載到結構上的載荷達到某一值時，若增加微小的載荷，而結構的位移卻發生很大的改變，通常將這種情況叫做結構屈曲，對應的載荷稱為屈曲載荷，這時的狀態稱為臨界狀態。根據臨界狀態的特性，屈曲可分為分支屈曲、極值屈曲和跳躍屈曲3種，分別對應圖5中的(a)、(b)和(c)所示的載荷-位移曲線[17]。

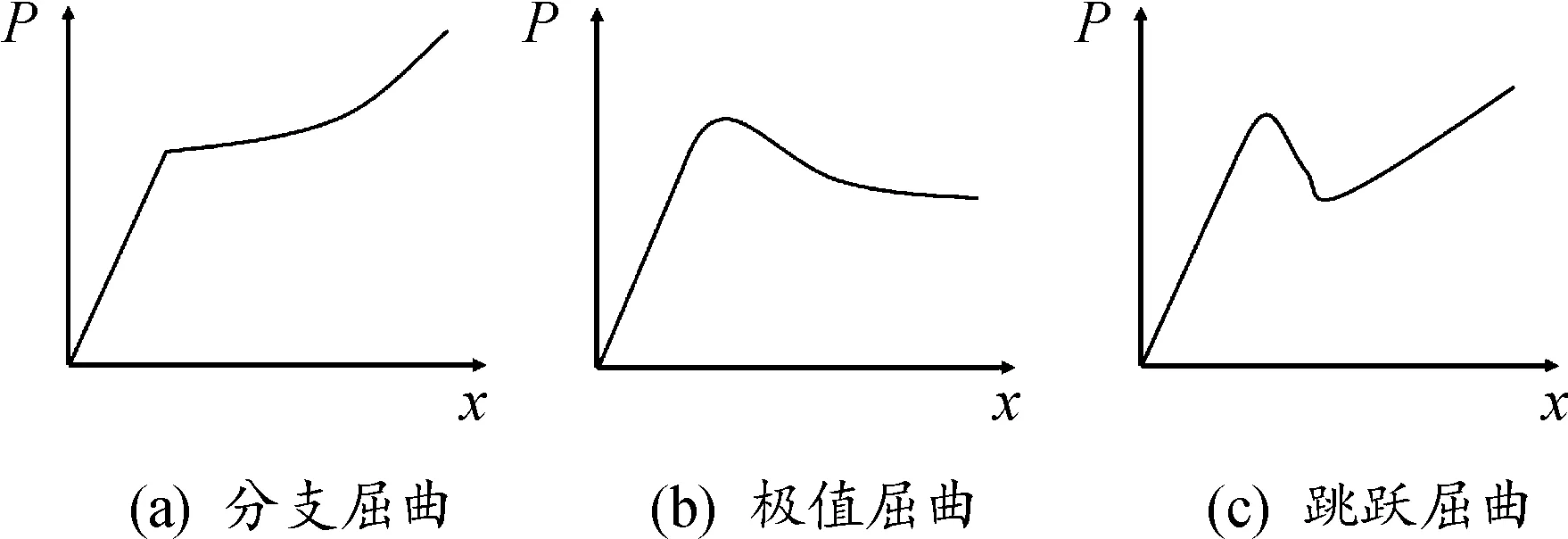
圖5 3種屈曲特性下的載荷-位移曲線

當球罐支柱的不均勻沉降量達到一定水平時，球罐在自重G、液體壓力p和支柱位移沉降量Sd等共同作用下，將發生整體或局部彎曲變形，導致結構屈曲。因此，需要對球罐開展屈曲分析，確定其不均勻沉降量的極限值。針對球罐的屈曲分析可采用“弧長法”。“弧長法”最初由Riks[18]提出，后經Crisfield[19]改進并逐漸得到完善，是目前結構屈曲分析中效率較高的方法。

非線性平衡方程組一般可以表示為：

K·x=F

(2)

其中矩陣K為切向剛度矩陣；向量x為節點位移；向量F為外載荷。現在將方程寫成增量形式，并引入一個載荷因子λ，平衡方程可以改寫成：

K·Δx=ΔλF

(3)

此時平衡方程共有n+1個未知量：Δx1，Δx1，…，Δxn，λ，而方程數量只有n個，因此需要補充一個約束條件：

Δλ2FTF+ΔxTΔx=Δl2

(4)

弧長法的求解流程如圖6所示，通過該流程的求解得到完整的沉降-位移關系曲線。弧長法是利用平衡方程和弧長約束條件尋找平衡點的過程，如圖7所示，表3中的球罐支柱的沉降量是逐步加載的，在加載過程中，前期OC段是屬于小變形的彈性階段，CD段及以后為大幅的屈曲變形階段。當沉降量超過C點所對應的沉降值時，球罐局部將會突然喪失原有的幾何形狀，發生大幅的屈曲變形，因此，可認為C點后球罐發生了屈曲。本文基于弧長法的數值模擬方法，分別研究球罐在3種沉降方式下的屈曲響應過程，以此來分析球罐變形與不均勻沉降之間的關系。

圖6 弧長法迭代求解過程框圖

圖7 弧長法迭代求解過程示意圖

3 結果分析

在應用Workbench平臺模擬球罐的屈曲響應過程中，表3中的球罐支柱的沉降量Sd是逐步加載的。載荷因子λ表示球罐屈曲響應過程中支柱不均勻沉降的加載比例，如λ=0.5時，球罐支柱加載的不均勻沉降為0.5Sd。當λ從0增大到1時，意味著球罐支柱的不均勻沉降全部加載完成。

圖8是通過Workbench求解得到的在單根沉降下的λ-xmax曲線，其中xmax為最大總位移，λ為載荷因子。圖9為該情形下的曲線中A、B、C和D點處的變形云圖，其中A、B、C和D點對應的λ值分別為0.15、0.3、0.45、0.55。

圖8 單根沉降下的λ-xmax曲線

圖9 單根沉降下球罐屈曲響應的變形云圖(變形縮放系數=20)

對照圖8、5可知，該球罐在單根沉降下的屈曲響應符合典型的分支屈曲的特點，在C點前球罐的變形隨支柱沉降的增大呈線性變化，且變形量較小，C點之前并未出現位移突變現象。說明在C點之前，球罐處于平衡狀態并未發生屈曲。C點時，球罐的變形云圖如圖9(c)所示，C點對應的最大總位移為13.5 mm(在支柱1的底部)。當支柱沉降量超過C點時(即λ>0.45)，球罐局部發生屈曲，如圖9(d)所示，此時最大位移為36.4 mm，屈曲主要發生在支柱1與支柱2之間的拉桿處。

圖10是通過Workbench求解得到的在蝶形沉降下的λ-xmax曲線。圖11給出了該情形下的曲線中A、B、C和D點處的變形云圖，其中A、B、C和D點對應的λ值分別為0.1、0.2、0.3和0.45。

圖10 蝶形沉降下的λ-xmax曲線

圖11 蝶形沉降下球罐屈曲響應的變形云圖(變形縮放系數=20)

對照圖10、5可知，該球罐在蝶形沉降下的屈曲響應也符合典型的分支屈曲的特點，在C點前球罐的變形隨支柱沉降的增大呈線性變化，且變形量較小，C點之前并未出現位移突變現象。說明在C點之前，球罐處于平衡狀態并未發生屈曲。C點時球罐的變形的云圖如圖11(c)所示，C點對應的最大總位移為7.5 mm(在支柱4的底部)。當支柱沉降超過C點時(即λ>0.3)，球罐局部發生了屈曲，如圖11(d)所示，此時最大總位移為55.8 mm，屈曲主要發生在支柱1與支柱12之間的拉桿處。

圖12是通過Workbench求解得到的在兩根沉降下的λ-xmax曲線。圖13給出了該情形下的曲線中A、B、C和D點處的變形云圖，其中A、B、C和D點對應的λ值分別為0.15、0.3、0.45和0.6。

圖12 兩根沉降下的λ-xmax曲線

圖13 兩根沉降下球罐屈曲響應的變形云圖(變形縮放系數=20)

對照圖12、5可知，該球罐在兩根沉降下的屈曲響應同樣也符合典型的分支屈曲的特點，在C點前，球罐的變形隨支柱沉降的增大呈線性變化，且變形量較小，C點之前并未出現位移突變現象。說明在C點之前，球罐處于平衡狀態并未發生屈曲。C點時球罐的變形的云圖如圖13(c)所示，C點對應的最大總位移為10.6 mm(在支柱1與球罐連接處)。當支柱沉降超過C點時(λ>0.45)，球罐局部發生了屈曲，如圖13(d)所示，此時最大總位移為44.1 mm，屈曲主要發生在支柱11與支柱12之間的拉桿處。

4 結論

1) 單根沉降的沉降極限值最大，蝶形沉降的沉降極限最小，說明球罐在單根沉降下比蝶形沉降更不易屈曲；球罐在單根沉降時屈曲變形最小，在蝶形沉降時屈曲變形最大，說明球罐在蝶形沉降下最危險，屈曲變形更嚴重。

2) 在球罐屈曲分析的前期階段，隨著沉降量不斷加載，球罐主要是發生小幅度的彈性變形，當沉降量超過沉降的極限值時(C點)，球罐將發生較大幅的屈曲變形，該球罐在3種不均勻沉降下的屈曲響應均符合典型的分支屈曲的特點。

3) 球罐的屈曲變形最大的位置位于拉桿處，合理選用剛度適宜的拉桿材料可以有效避免拉桿屈曲；其次，屈曲變形較大的位置是沉降的支柱與球殼連接的位置。