基于注意力機制的CNN-GCN模型及其應用
李繼龍,霍緯綱+,李 勤
(1.中國民航大學 計算機科學與技術學院,天津 300300; 2.京北方信息技術股份有限公司 IT服務交付中心部北京平臺,北京 100032)
0 引 言
多變量時間序列預測在經濟學、金融[1]、生物信息學和交通[2,3]等領域有著巨大的應用。多變量時間序列預測方法內在地假定變量之間有相互依賴關系。換句話說,每個變量不僅取決于其歷史值,而且還取決于其它變量。然而,現有的方法并沒有有效地利用變量之間潛在的相互依賴關系。首先考慮多變量時間序列(multivariate time series,MTS)的統計方法。如自回歸(autoregressive,AR)模型和高斯過程(Gaussian process,GP)模型是經常用到的基線方法。二者均假設變量之間存在線性依賴關系。為了建立非線性關系,采用了AR的一些變體,如向量自回歸多層感知器(vector autoregressive multi-layer perceptron,VARMLP)模型。最近基于深度學習的MTS預測方法得到了快速發展,依次提出了卷積神經網絡(convolutional neural network,CNN)模型[4]、門控循環單元循環神經網絡(gated recurrent unit recurrent neural networks,RNN-GRU)模型[5]、長短期時間序列網絡(long-and short-term time-series network,LSTNet)模型[6]、雙自注意力網絡(dual self-attention network,DSANet)模型[7]和用圖神經網絡進行多變量時間序列預測模型(multivariate time series forecasting with graph neural networks,MTGNN)[8]。
上述方法大多從提取MTS時序特征角度建立了預測模型,DSANet和MTGNN預測模型同時考慮MTS的時間和空間特性,但是DSANet中采用的自注意力機制無法很好表達MTS各變量間的依賴關系,MTGNN采用圖卷積網絡提取了MTS的變量之間的空間依賴關系,但其捕獲時序特征的子模塊較復雜。為了實現對多變量時間序列準確和穩健的預測,本文提出了一種融入圖卷積網絡、注意力機制和卷積神經網絡的三通道網絡框架模型,實驗結果表明了本文中所提出的模型方法有較好的MTS預測效果。
1 背景知識
1.1 GNN和GCN
圖神經網絡[9](graph neural network,GNN)在處理網絡中實體之間的空間依賴關系方面取得了巨大成功。圖神經網絡假設節點的狀態取決于其鄰居的狀態。為了捕捉這種類型的空間依賴,通過消息傳遞[10]、信息傳播[11]和圖卷積[12]開發了各種圖神經網絡。Marco Gori等發表論文,提出了圖神經網絡的概念。隨后,其在兩篇論文中又進一步闡述了圖神經網絡,并提出了一種監督學習的方法來訓練GNN。圖卷積網絡(graph convolutional network,GCN)是GNN的一種,采用卷積算子進行信息匯聚。卷積神經網絡在視覺領域取得令人矚目的成績,于是人們開始考慮如何將卷積應用到圖神經網絡中。Kipf等[12]將頻域圖卷積的定義進行簡化,使得圖卷積的操作能夠在空域進行,這極大地提升了圖卷積模型的計算效率,同時,得益于卷積濾波的高效性,圖卷積模型在多種圖數據相關的任務上取得了令人矚目的成績。近幾年,更多的基于空域圖卷積的神經網絡模型的變體[13,14,10]被開發出來。
1.2 注意力機制
注意力機制[15]就是讓神經網絡具備有選擇的去關注輸入中的某一部分的細節信息的能力。注意力機制允許對依賴關系進行建模,而不考慮它們在輸入或輸出序列中的距離。注意力機制自從被提出以來就受到了人們的關注和追捧。因其良好的性能效果,已成功的在多個領域的多個任務上得到了應用。
自注意力(又稱內部注意力),是注意力機制的一種形式,它涉及單個序列的不同位置,用以計算序列的表示。自注意力機制已成功地應用于多種任務,比如閱讀理解、文本摘要、文本蘊涵和與任務無關的句子表示學習[16]等。多頭注意力就是根據多個查詢來計算和選取多個信息的。多頭注意力能夠很好模擬人類視覺注意力機制的原理過程。在很多任務中的序列建模和構建轉導模型時,多頭注意力機制成為可供選擇的一個很好的組成部分。
2 問題描述
時間序列X(i)=〈x1(i),x2(i),…,xT(i)〉 是一個一維時序測量序列,其中數量XT(i)是在時間戳T的記錄。通常,兩個連續測量之間的時間間隔是恒定的。多變量時間序列表示為X=〈X(1),X(2),…,X(D)〉, 其中X中的時間序列相互關聯,向量XT∈D是在時間戳T的記錄。
給定一組多變量時間序列X=〈X(1),X(2),…,X(D)〉, 其中D是單變量時間序列的數目,X(D)∈T,T是輸入窗口的長度,本文以滾動預測的方式進行多變量時間序列的預測。也就是說,基于已知的 〈X1,X2,…,XT〉 來預測XT+h,其中h是當前時間戳前面可取的時間間隔范圍(Horizon)。同樣,基于 〈X1+k,X2+k,…,XT+k〉,k∈+預測未來XT+h+k的值,假設窗口內的信息足以滿足預測需求,窗口大小是固定的。因此,設定預測目標XT+h∈D, 在時間戳T的輸入矩陣為X=〈X(1),X(2),…,X(D)〉∈D×T。
3 基于注意力機制和圖卷積的神經網絡模型
3.1 時間序列預測模型的整體架構
基于圖卷積網絡和注意力機制,構建一種多變量時間序列預測模型簡記為DSAGCN(dual self-attention graph convolutional network),本文稱之為“基于注意力機制的CNN-GCN”,其整體的框架結構如圖1所示。
基于注意力機制的CNN-GCN模型由圖學習層模塊、圖卷積層模塊、局部時間卷積模塊、全局時間卷積模塊、自注意力模塊和輸出模塊6部分構成,詳細介紹如下。
圖學習層模塊自適應地學習圖的鄰接矩陣,以捕獲MTS各序列之間的空間依賴關系。M(本文中M取的是5)個圖卷積模塊間加入了殘差連接跳躍連接,以圖的鄰接矩陣和MTS數據樣本為輸入,聚合MTS各序列與其鄰接序列的特征。局部卷積模塊通過卷積單元、池化單元、自注意力單元和前饋神經網絡單元4部分,提取MTS數據樣本的局部時態特征。類似地,全局時間卷積模塊通過卷積單元、自注意力單元和前饋神經網絡單元三部分,提取MTS數據樣本的整體時態特征。自注意力模塊分別捕獲全局時間卷積和局部時間卷積結果的時態空間依賴關系,并將結果同時輸入進全連接層。最終將全連接層的輸出與圖卷積模塊的輸出相加得到整個模型方法的預測值。
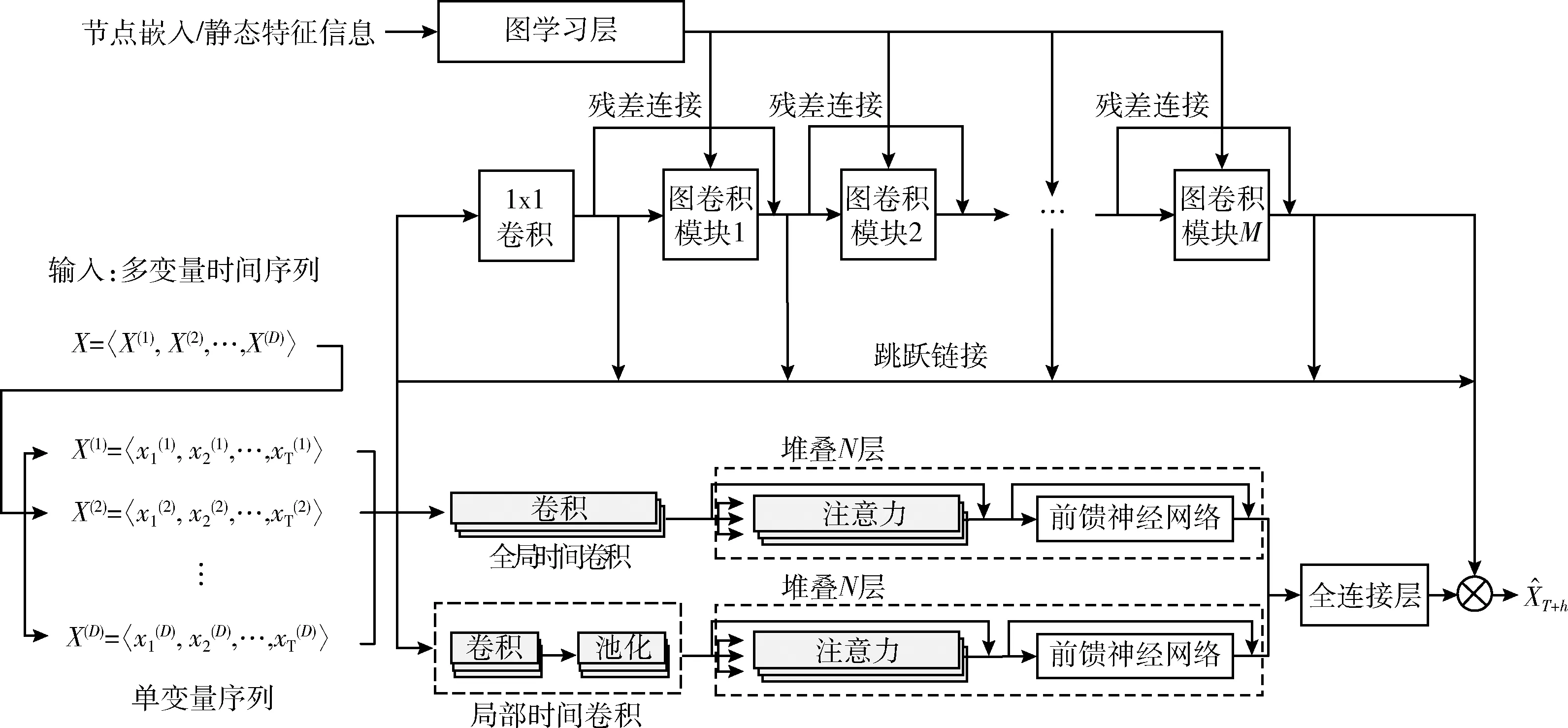
圖1 基于注意力機制的CNN-GCN模型的整體框架結構
3.2 圖學習層模塊
DSAGCN采用圖學習層自適應地學習對應于MTS樣本的鄰接矩陣[8],以圖的形式學習MTS各變量時間序列之間隱藏的空間依賴關系。該模塊可以學習MTS各變量之間的單向依賴關系,能更好適用于MTS的預測任務。具體學習方法如式(4)~式(6)所示
M1=tanh(αE1Θ1)
(1)
M2=tanh(αE2Θ2)
(2)
A=ReLU(tanh(α(M1M2T-M2M1T)))
(3)
fori=1,2,…,D
(4)

(5)
A[i,-idx]=0
(6)
其中,E1、E2表示隨機初始化的節點嵌入,Θ1、Θ2為全連接網絡的參數,用于隨機初始化節點嵌入之間的依賴權重大小,Θ1、Θ2會隨著訓練的進行而學習到適合的權重以擬合MTS變量之間的空間依賴關系,α是控制激活函數飽和率的超參數。式(3)通過每個節點對之間正向依賴與反向依賴相減,將依賴關系轉化為非對稱性依賴,最終通過ReLU激活函數對鄰接矩陣進行正則化。最后對于每個節點,選擇它的top-k最近的節點作為它的鄰居,在保留連接節點的權重的同時,將非連接節點的權重設置為零。
3.3 圖卷積模塊
圖卷積模塊按3.2節圖學習模塊生成的鄰接矩陣,以卷積的方式實現多維時間序列中具有空間依賴性的變量之間的特征聚合。圖卷積模塊由兩個混合跳傳播層組成,分別處理通過每個節點的流入和流出信息。通過添加兩個混合跳傳播層的輸出來獲得單向流入信息。圖2顯示了圖卷積模塊和混合跳傳播層的網絡結構[8]。圖2(a)中的T′表示鄰接矩陣A轉置。
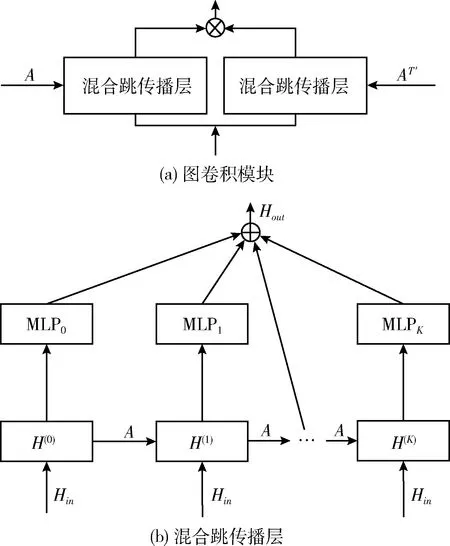
圖2 圖卷積和混合跳傳播層
圖2(b)為混合跳傳播層的網絡結構。圖中A表示圖學習模塊學習得到的鄰接矩陣,Hin為圖卷積網絡模塊上一層的輸出,混合跳圖卷積的信息傳播和選擇過程按式(7)、式(8)進行
(7)
(8)
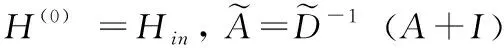
3.4 全局時間卷積模塊
相比于RNN的迭代性和順序性,卷積結構已經被證明在捕獲特征和并行計算方面的能力,可以提升對于長序列的計算速度和預測效果,DSAGCN采用全局時間卷積模塊用于提取MTS單變量時間序列所有時間步的時序特征[7]。具體卷積計算方式如式(9)所示
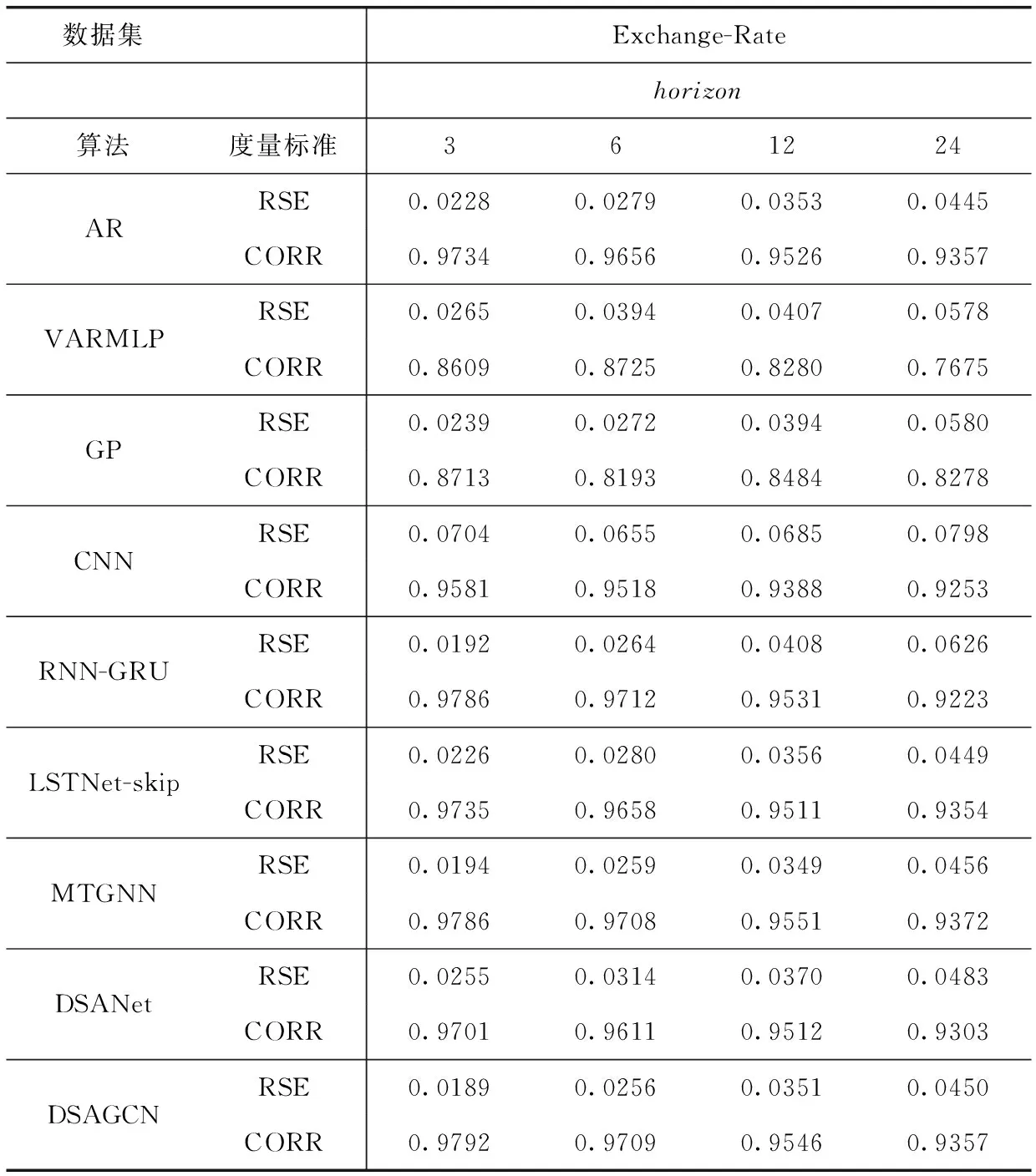
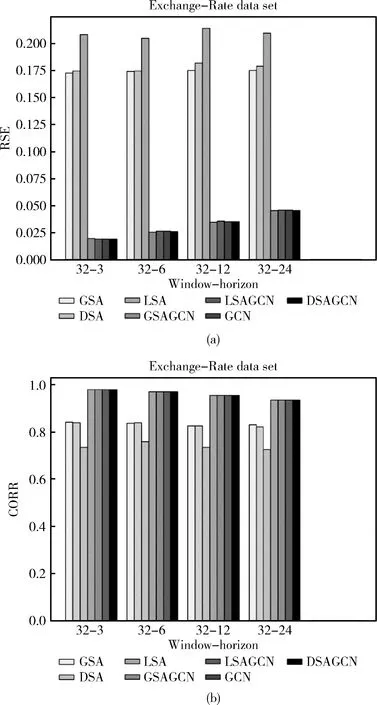
HG=RELU(Wk*X+bk) (0 (9) 式中:*表示卷積運算,Wk為第k個卷積核,文中用nG個T*1大小的卷積核對輸入時間序列樣本X∈RD*T進行全局卷積。那么D維的時間序列樣本X由卷積運算生成一個D*1的向量。輸入樣本X由nG個卷積核得到一個大小為D*nG的輸出矩陣HG。HG中每行中的元素表示不同權重的卷積核提取的不同屬性的特征。 與全局時間卷積提取MTS各序列的固定時態特征,局部卷積側重于建模MTS序列內部的局部時態模式[7]。文中局部時間卷積模塊使用長度為l的卷積核進行卷積運算,以提取MTS序列內部局部上下文信息。對MTS樣本X的第i維序列X(i)進行一次步長為s的類似式(9)的卷積操作,生成長度為Out=(T-L)/s+1嵌入向量。X的局部時間卷積結果生成矩陣MkL∈RD*o ut, 然后使用最大池化操作捕獲MkL中最突出的特征。X的最終局部時間卷積運算結果為D維向量。和全局卷積模塊相同,每個樣本X由nL個卷積核生成表達局部時態信息的特征矩陣HL∈RD*nL。 文中還采用了自注意力機制進一步捕獲MTS樣本中各序列間的空間依賴關系[7]。該模塊計算了3.4節和3.5節中全局時間卷積模塊和局部時間卷積模塊的輸出矩陣HG和HL各行之間的注意力大小。下面具體說明全局時間卷積模塊輸出矩陣HG的各行之間注意力計算過程。 HG中的每一行記為X′,由式(10)~式(12)生成X′的查詢、鍵和值矩陣QG、KG和VG。由式(13)計算HG各行之間的注意力得分。dκ是鍵的維數 QG=WQ*X′ (10) KG=WK*X′ (11) VG=WV*X′ (12) (13) (14) 位置前饋層由兩個線性變換組成,在其間有一個ReLU作為激活函數,可以表示為 (15) 類似的,對于局部時間卷積后的自注意力模塊與上述計算過程相同,HL經文中自注意力模塊后的輸出記為FL。 (16) (17) 模型的評估指標采用文獻[6]使用的相對平方根誤差(toot telative squared error,RSE、RRSE)和經驗相關系數(empirical correlation coefficient,CORR)兩個傳統評估指標。這兩個評估指標可以用公式如下表示 (18) (19) 匯率(Exchange-Rate)數據集:收集澳大利亞、英國、加拿大、瑞士、中國、日本、新西蘭和新加坡等8個國家從1990年到2016年不等的每日匯率數據。 在本文進行的實驗中,數據集按時間順序分為訓練集(60%)、驗證集(20%)和測試集(20%)。在每一組中,使用滑動窗口將數據進一步分割成多個情況,這意味著在每一段中,使用T長度的多變量時間序列作為模型的輸入數據,并使用在T+h時間戳的數據作為真實數據。 實驗主要考慮了8個基線模型方法:AR、VARMLP、GP、CNN、RNN-GRU、DSANet、MTGNN、LSTNet-skip。而這些方法在引言中均已涉及提到。LSTNet-skip是文獻[6]提出的一種融合了循環跳躍連接模塊的LSTNet模型。 本文涉及的神經網絡模型都是通過使用Adam優化器[17]執行小批量隨機梯度下降(mini-batch SGD)來優化的。根據文獻[8]設置進行實驗的窗體大小(window size)為32,學習率為0.0001,梯度裁剪(clip gradient)為5,權重衰減率為0.000 01,訓練步長為100,圖學習層模塊中的超參數α=3,圖卷積模塊數M=5,每個圖卷積模塊的層數為2,圖卷積層模塊中的超參數β=0.05,全局時間卷積的卷積核為(32,1),局部時間卷積的卷積核為(3,1),池化為最大池化,自注意力堆疊層數N=6,回歸損失函數采用L1Loss即平均絕對誤差L1損失。其它基線模型的參數設置依據原論文的參數設置。 本文涉及的模型方法均是在python3.7.6中實現的,其中深度學習方法是在Py-Torch1.2.0版本上實現的,所有實驗均是使用配置英特爾i7-7700CPU、8核、16 GB RAM、NVIDIA Quadro P2000的機器運行的。 表1概括總結了在國際匯率數據集上實驗涉及到的所有9個模型方法在RSE和CORR兩個評價標準上的評估結果。分別設置horizon={3,6,12,24}, 即設置horizon從3天到24天不等用于預測。從進行的實驗情況可以看出horizon越大,對任務進行預測就越難。在horizon=3、6時本文提出的DSAGCN模型的預測效果最好,說明預測步長較小時,DSAGCN模型能夠較好提取和利用時空依賴關系特征來提高預測效果。當horizon=12、24時AR模型和MTGNN模型預測效果較好,表明預測步長較大時,DSAGCN模型就不如AR模型和MTGNN模型的預測效果了,但預測精度差別不大。從總體性能上來說本文提出的DSAGCN模型在所用實驗數據集上的預測性能是優于其它基線模型的。 圖3展示了消融實驗各模型情況。GSA(global self-attention network)表示只有全局時間自注意力一個通道的模型,LSA(local self-attention network)表示只有局部時間自注意力一個通道的模型,GCN表示只有一個圖卷積通道的模型(當然也有圖學習模塊),DSA(dual self-attention network without AR)表示有全局時間自注意力和局部時間自注意力兩個通道的模型,GSAGCN(global self-attention and graph convolutional network)表示有全局時間自注意力和圖卷積兩個通道的模型,LSAGCN(local self-attention and graph convolutional network)表示有局部時間自注意力和圖卷積兩個通道的模型,DSAGCN表示本文提出的三通道模型。 從圖3(a)可以看出LSA模型的RSE值最大;DSA和GSA兩模型的RSE值依次較大;GSAGCN、LSAGCN、GCN和DSAGCN這4個模型的RSE值較小,而這4個模型是都含有GCN模塊或者說GCN通道的。 表1 不同模型在數據集上的單步預測實驗情況 圖3 消融實驗情況 從圖3(b)可以看出LSA模型的CORR值最小;DSA和GSA兩模型的CORR值較小;GSAGCN、LSAGCN、GCN和DSAGCN這4個含有GCN模塊的模型的CORR值較大。RSE值越小,CORR越大,則說明模型越好。從消融實驗的結果圖3(a)、圖3(b)可以分析出:含有GCN模塊的4個模型均較好,所以說GCN通道對模型預測精度的貢獻較大,能夠很大程度上影響模型的好壞。說明GCN通道所采用的圖學習層模塊能夠通過很好地自適應地學習圖數據的鄰接矩陣,來捕獲時間序列數據之間隱藏的空間依賴關系,圖卷積層模塊通過圖卷積操作很好地處理了圖學習層模塊學習到的圖中的空間依賴關系。在GCN通道上再加入另外兩個通道,模型性能又有了一定程度提高,說明全局自注意力通道和局部自注意力通道提取到的特征信息可以在一定程度上提高本文提出的DSAGCN模型方法的預測精度。所以說3個通道對模型的預測精度均有貢獻,均能一定程度上提高模型的預測精度。 本文提出了基于深度學習的一種多變量時間序列預測模型DSAGCN。DSAGCN利用圖卷積神經網絡GCN提取多變量時間序列變量之間的空間依賴關系特征,利用卷積神經網絡CNN和注意力機制提取多變量時間序列的前后長短期時間片段的時間依賴關系特征,然后融合多變量時間序列的時間和空間依賴關系特征進行預測。在國際匯率(Exchange-Rate)數據集上進行應用的實驗結果表明本文提出的模型在各方面的綜合性能是優于本文提及的基于深度學習的其它基線模型的。DSAGCN模型可以在交通流預測、農業勞動力供給預測、網絡輿情預測、商品銷售量預測等等具體的領域中做進一步應用。3.5 局部時間卷積模塊
3.6 自注意力模塊

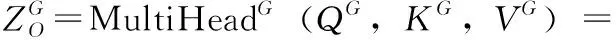
3.7 預測結果的輸出
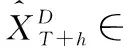
4 實驗及結果
4.1 評價標準
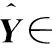
4.2 實驗數據介紹
4.3 實驗詳述
4.4 實驗結果及分析
5 結束語

