微慣性接電開關載荷識別機構設計中的能量分析法

黃 巍，聶偉榮，席占穩，曹 云

(南京理工大學機械工程學院，江蘇 南京 210094)

0 引言

微機電系統(micro electro mechanical systems，MEMS)因其功耗低、尺寸小、易集成、可批量生產等優點在工業生產中得到了迅速發展，在汽車、消費電子、航天航空、生物醫療、智能通信等行業領域得到了廣泛的應用[1-2]。微慣性開關又被稱作微加速度開關、微閾值加速度計，是基于MEMS工藝技術加工、集傳感器與執行器于一體的微慣性器件，通常情況下其處于斷開狀態，只有在外部施加的加速度載荷超過特定值(閾值)時才會閉合并接通電路[3]。發展日益完善的微慣性開關，因MEMS技術的獨特優勢而逐漸應用在汽車安全、智能穿戴和武器準備等領域中[4-6]。

針對某些特定應用場景使用的微慣性開關，如應用于引信電源系統的微慣性接電開關(以下簡稱為接電開關)，除了要能夠穩定導通以外，為防止運輸或其他勤務處理時因意外跌落導致出現安全問題，還應具備發射載荷和勤務跌落載荷的載荷識別功能，保證在勤務跌落環境下接電開關不會閉合而在發射環境下可以正常閉合。為實現這一功能，研究者們在接電開關中加入了載荷識別機構。文獻[7]基于曲折槽式后坐保險機構分析并設計了相應的環境識別機構，然而該種類型的機構由于層間結合力較小，導致其在高過載下容易出現分層脫離現象。文獻[8—9]設計了抗高過載性能更為優秀的齒形結構。文獻[8]僅從位移響應上對機構的特征參數進行了分析與設計，沒有從工作原理上進行闡述和分析；文獻[9]將載荷識別機構等效為一阻尼常數，結果表明整體位移響應曲線更加匹配，然而這一等效阻尼模型無法描述單次碰撞過程，亦無法描述機構特征參數的影響。本文在文獻[9]的基礎上，針對原有設計方法中存在的局限性，提出一種能量分析法，這種方法從載荷識別機構的工作原理進行分析，并且能夠更好地描述單次碰撞過程，從而描述特征參數對機構的影響，可以作為輔助設計方法。

1 載荷識別機構工作原理

1.1 接電開關工作原理

載荷識別機構為接電開關的一部分，要想解釋機構的工作原理需要先分析接電開關的工作原理。開關物理模型如圖1所示，為兩個質量-彈簧-阻尼系統的串聯系統。質量塊m1、彈簧k1和阻尼c1組成環境響應模塊，用以感受外部加速度并產生質量塊m1的位移響應y(t)；鎖頭m2、彈簧k2、阻尼c2和閉鎖梁則組成接電模塊，這一部分為開關的電極部分，用以和外部電路連接。質量塊m1在慣性力作用下運動到與鎖頭m2相碰后，推動鎖頭m2一起運動，鎖頭m2撐開閉鎖梁并繼續向前運動一段位移后，發生彈性回落并在閉鎖梁限制下形成閉鎖，實現電路的穩定接通。

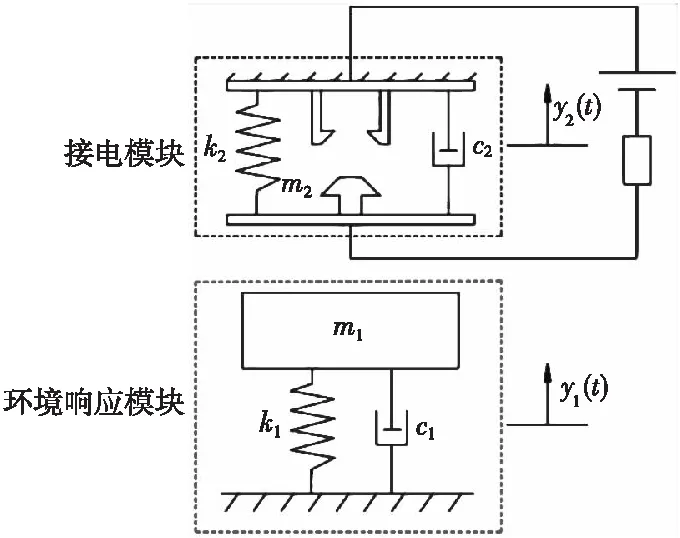
圖1 微慣性接電開關物理模型示意圖Fig.1 Schematic diagram of physical model of micro-inertial power switch

1.2 載荷識別機構結構分析

載荷識別機構為圖2所示的齒形機構，作用于環境響應機構。單齒的特征參數包括齒形角β、齒高H和重合度γ，其決定了單齒的結構。該機構包括多組齒對，其中附加在質量塊m1上的齒作為主動齒對，附加在兩側固定桿上的齒為被動齒對。質量塊m1在外部載荷的作用下向敏感方向運動，在運動過程期間主動齒與被動齒發生碰撞，從而發生能量損失，在不同類型載荷下能量損失存在差異，進而實現載荷的識別。

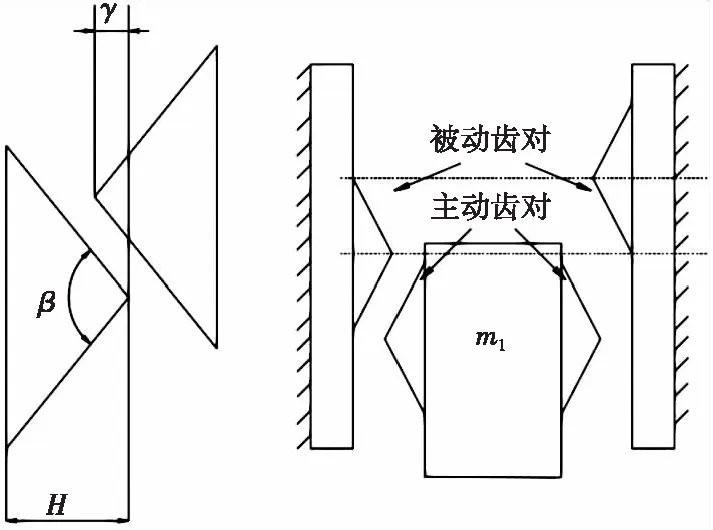
圖2 齒形載荷識別機構示意圖Fig.2 Schematic diagram of teeth damping mechanism

2 能量分析法

能量分析法從系統能量得失角度去研究問題。在環境響應系統的運動過程中，能量來源為慣性力所做的正功，而能量損耗主要為齒與齒之間的碰撞(與接電模塊接觸前)。以下分別從慣性力正功和碰撞動能損失兩方面介紹能量分析法。為便于分析，以兩種典型載荷：幅值8 000g、脈寬2 ms的發射載荷(以下簡稱載荷1)和幅值15 000g、脈寬100 μs的勤務跌落載荷(以下簡稱載荷2)為研究對象。

2.1 慣性力正功

環境響應模塊的能量來源是慣性力所做正功，即慣性力在質量塊m1達到最大位移前做的功，可由式(1)求得：

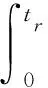
(1)

式(1)中，tr為環境響應模塊達到最大位移的時間，F是慣性力，v是環境響應模塊的速度。以上值均可通過以下各式求得[9]：

F(t)=ma0sinω0t

(2)

(3)

(4)

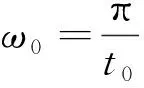
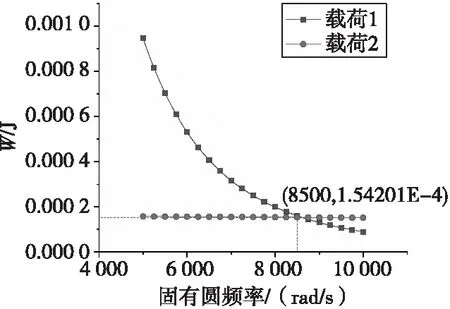
圖3 慣性力對環境響應模塊所做正功Fig.3 Positive work done by inertia force to environmental response module

2.2 碰撞動能損失

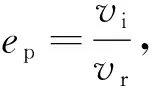
(5)

式(5)中，vy為碰撞物體的屈服臨界速度，是一個與物體材料屬性、表面形貌等相關的參數。由式(5)可以得到物體的動能變化：

(6)

由式(6)可知，當碰撞物體結構和材料屬性確定時，其動能變化量只與碰撞初速度vi相關，其變化曲線如圖4所示，動能損失隨碰撞初速度vi增大而增大。故而可以通過分析質量塊m1在兩種載荷下的碰撞初速度來判斷其產生的動能損失差異。

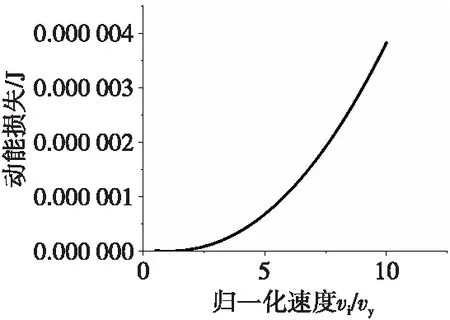
圖4 動能損失與初速度之間的關系Fig.4 The relationship between kinetic energy loss and initial velocity

設載荷1作用下質量塊m1的速度為v1，碰撞動能損失為ΔE1；載荷2作用下質量塊m1的速度為v2，碰撞動能損失為ΔE2。由式(3)、式(4)計算得到的不同位移和固有頻率下的v1和v2如圖5所示。可以看出，相同位移、相同固有頻率下v1始終小于v2，即ΔE1<ΔE2。

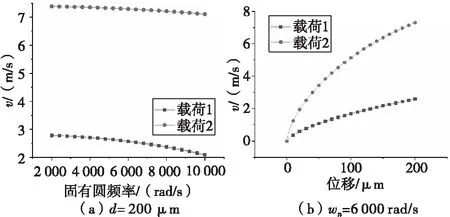
圖5 質量塊m1速度的變化曲線Fig.5 The variation curve of m1 velocity of mass block

綜上所述，對于環境響應模塊固有圓頻率小于8 500 rad/s的接電開關，均滿足ΔE1<ΔE2(相同位移下)和W1>W2的條件，通過設計合理的齒形載荷識別機構特征參數，即可實現對載荷1和載荷2的識別，且應可以實現對具有不同幅值、脈寬的兩種載荷的識別，即具有普適性。

3 仿真分析

3.1 基于能量分析法的齒形特征參數分析

應用能量分析法，對載荷識別機構特征參數進行能量分析，并結合工藝要求提出對特征參數選取的要求。載荷識別機構通過影響環境響應模塊運動過程中的動能損失工作，對慣性力正功影響較小，故以下只分析各特征參數對動能損失的影響。表1列出了接電開關的相關參數，作為仿真計算的基礎數據。

表1 微慣性接電開關相關參數Tab.1 Parameters of micro inertia power switch

齒形角對動能損失的影響如圖6(a)所示。系統的動能損失量和動能損失變化率均隨著齒形角的增大而減小。齒形角是比較敏感的結構參數，應盡量減小加工誤差帶來的影響，因此齒形角應優先選擇鈍角；并且考慮到過大的齒形角參數會導致整體機構在敏感方向上的尺寸較大，因此應綜合考慮影響后選擇一個折中值。

動能損失與齒高的關系如圖6(b)所示。齒高對動能損失的影響不大，只有非常小的波動。這是由于齒高的改變并沒有改變碰撞的接觸面積，整體上看對動能損失幾乎沒有影響。齒高決定了齒形的基本大小，齒高過大會導致整體尺寸過大，而齒高過小則不宜于加工。因此在這一參數對性能影響較小的情況下，應取一個中間數值。

重合度γ是指一組齒之間齒頂的相對間隙。通過計算得到的不同速度下動能損失與重合度的關系如圖6(c)所示。由圖所示，重合度對系統動能損失的影響整體上是線性的。這是由于重合度對齒與齒之間的接觸面積的影響是線性的，而接觸面積對摩擦力做功的影響也是線性的，所以重合度對動能損失的影響也是線性的。重合度是一組齒對之間的重要參數，在工藝加工中也是最容易出現較大加工誤差的參數。由于過大的重合度會增大加工誤差的影響，所以重合度應控制在較小的數值。

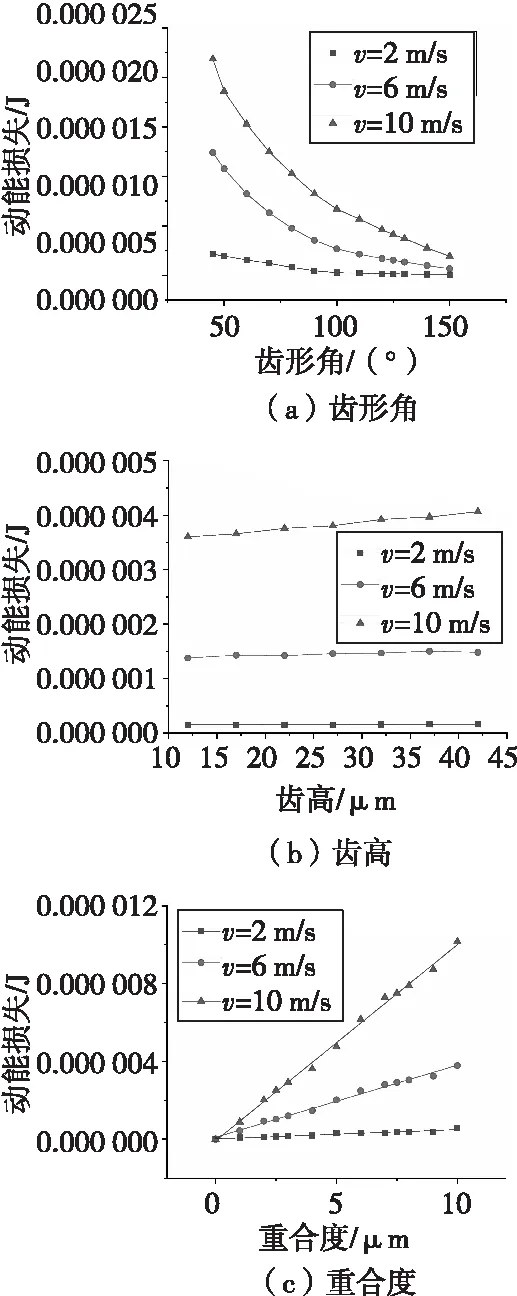
圖6 各齒形結構參數對動能損失的影響Fig.6 Effect of tooth structural parameters on kinetic energy loss

通過上述單齒特征參數能量分析，結合工藝要求，確定單齒特征參數為：齒形角125°，齒高32 μm，重合度4 μm。由于多次碰撞是一個連續過程，因此需要對整體過程的能量得失進行分析。以下針對幅值8 000g、脈寬2 ms的發射載荷(載荷1)和幅值15 000g、脈寬100 μs的勤務跌落載荷(載荷2)，對載荷識別機構的齒數比進行能量分析。同理，主要對碰撞動能損失進行分析。

通過仿真計算得到在不同齒數比的齒形載荷識別機構作用下的質量塊m1的動能損失曲線如圖7所示。設載荷1下的動能損失為ΔE1m，載荷2下的動能損失為ΔE2m。圖7(a)表示了不同齒數比下ΔE1m和ΔE2m的變化情況，在同一齒數比下，ΔE1m始終小于ΔE2m，這與之前的分析是一致的。圖7(b)顯示了不同齒數比下動能損失比ΔE1m/ΔE2m的變化，理論上這一值越小，質量塊m1在兩種典型載荷下由于齒形載荷識別機構產生的碰撞動能損失差異越大，載荷識別效果越好。然而這一數值來看，1∶2的齒數比應該具有最好的載荷識別效果，但是無法說明載荷識別的可靠性，故要結合位移響應分析進一步分析。

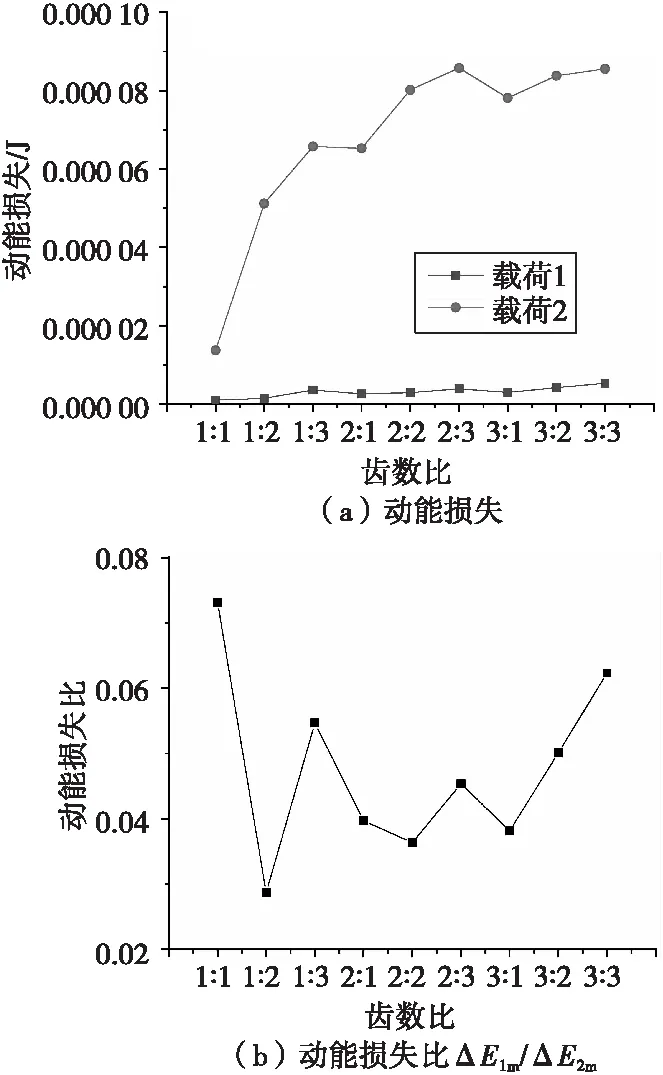
圖7 不同齒數比下質量塊m1的動能損失Fig.7 Kinetic energy loss of massm1 under different teeth number ratio

設質量塊m1與齒形載荷識別機構作用后的最大位移分別為y1max(載荷1作用)和y2max(載荷2作用)。圖8為不同齒數比下y1max和y2max比較的柱狀圖，其中各基準線為在各個齒數比下質量塊m1上主動齒全部通過固定桿被動齒的最小位移，為實現可靠區分，y1max應大于這一值而y2max應小于這一值。(由于固定桿本身體積對質量塊存在阻擋作用，使其后續運動受到限制，所以其最大位移只有1.26 mm。)由圖8可知，當齒數比為1∶2時未能實現可靠載荷識別，故單從能量方面無法驗證載荷識別的可靠性，需要結合位移響應進行分析。而單從位移響應方面無法得到最優的特征參數，當齒數比為2∶3、3∶2、3∶3時均可實現可靠的載荷識別，而通過能量分析，即可從這些備選參數中選擇最優值，即動能損失比最小的2∶3。

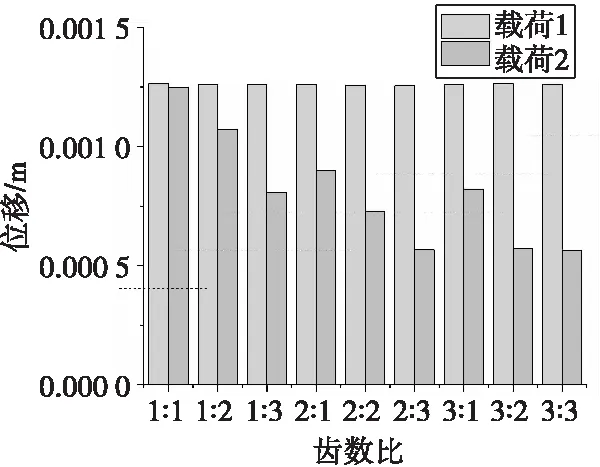
圖8 不同齒數比下質量塊m1的最大位移Fig.8 The maximum displacement of mass m1 under different teeth number ratio

3.2 基于能量分析法的載荷識別普適性分析

設發射載荷的幅值為A1，脈寬為T1；勤務跌落載荷的幅值為A2，脈寬為T2。通常情況下，A1在1 000～30 000g之間，T1在2～8 ms之間；A2在8 000～15 000g之間，T2在100～300 μs之間[12-13]。以下基于能量設計法，對載荷識別機構的適用性進行計算分析，驗證其能否適用于不同幅值、脈寬的發射載荷和勤務跌落載荷的載荷識別。設定基礎參數初始碰撞距離為200 μm，環境響應模塊的固有圓頻率為1 000 rad/s。

圖9為慣性力所做正功W1和W2分別隨T1和T2變化的關系曲線。由圖9可知，W1隨T1增大基本呈上升趨勢，當T1≈5 ms時達到最高點，之后又減小；W2隨T2增大而增大，當T2=300 μs時達到最大值。除A1=1 000g外，W1的曲線基本均在W2的上方，對于大部分載荷均滿足W1>W2。

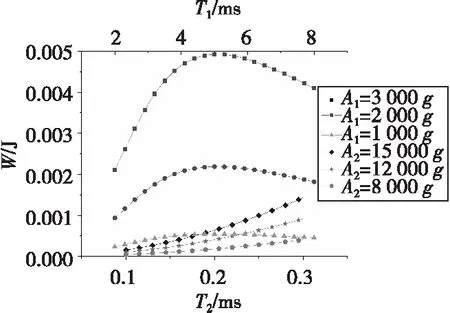
圖9 不同載荷下慣性力所做正功Fig.9 Positive work done by inertia force under different loads

圖10為相同位移下質量塊m1的速度v1和v2分別隨T1和T2變化的關系曲線。圖10中，v1隨T1增大先短暫增大，當T1≈3 ms時達到最高點，之后則減小；v2隨T2增大而減小，當T2=300 μs時達到最小值。可以看出，v1始終小于v2，即碰撞動能損失ΔE1始終小于ΔE2。

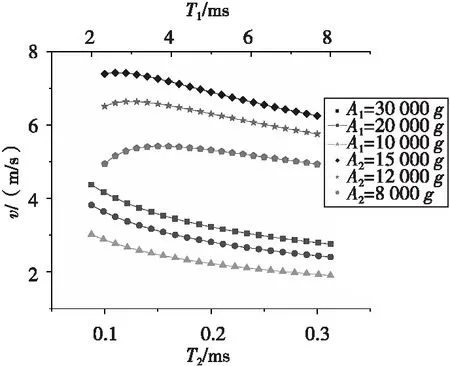
圖10 不同載荷下質量塊m1碰撞初速度Fig.10 Collision velocity of mass m1 under different loads

綜上所述，通過設計不同的齒形載荷識別機構的特征參數(齒形角、尺高、重合度、齒數比等)，可實現對不同幅值、脈寬的兩種類型載荷的載荷識別，即齒形載荷識別機構對于載荷識別具有普適性。

4 結論

本文提出微慣性接電開關載荷識別機構設計的能量分析法，該方法基于載荷識別機構的工作原理，通過不同類型載荷下碰撞的能量損失的差異來實現載荷識別，從開關系統的能量得失角度，即慣性力正功和碰撞動能損失兩方面對開關對于發射載荷和勤務跌落載荷的識別能力進行分析。仿真驗證結果表明，可以更好地描述單次碰撞過程并且在載荷識別機構的設計中，該方法可以作為輔助設計方法以得到設計參數的優選值，并且基于此方法對載荷識別機構的適用性進行了分析，結果表明該機構具有普適性。