轉動驅動圓角立方體顆粒有序堆積的離散元模擬1)

張 祺 喬 婷 季順迎 厚美瑛

* (中國科學院物理研究所,北京 100080)

? (太原理工大學機械與運載工程學院,太原 030024)

** (大連理工大學工業裝備結構分析國家重點實驗室,遼寧大連 116023)

引言

熱系統中無序的粒子在熱驅動下進行重新排列,自發形成有序的結構,稱為自組裝過程[1-2].作為非熱學流,盡管熱運動對顆粒物質的影響可以忽略(mgd?kBT),但容器的振動[3-5]、旋轉[6]、敲擊[7]、剪切[8-9]以及重力驅動下自身流動[10]也可以發揮熱漲落的驅動作用,改變顆粒體系的構型,達到整體或者部分顆粒有序堆積的效果.宏觀顆粒有序堆積過程為研究微觀粒子系統自組裝問題提供了很好的借鑒.

顆粒的有序堆積必然伴隨顆粒系統的密實化過程,這不僅涉及拓撲結構、對稱性等顆粒系統結構優化問題,而且對提高交通運輸、包裝工業、工農業生產中顆粒材料的空間利用率具有重要現實意義[11].研究發現三維單分散球體的最密隨機堆積(random close packing,RCP)體積分數約為0.64[12-13],更高體積分數尤其是最密規則堆積的三維單分散球體結構則需要一些繁復的方法才能實現.Carvente等[14]利用一種類似退火的方式(振動強度逐漸降低)實現了三維方形容器中的等大鋼球從初始的顆粒氣體狀態逐漸形成體心四方或者面心立方結構.Yu 等[15]通過一個類似晶體外延生長的方式向振動顆粒床中逐步添加球體最終實現了三維的最密規則堆積結構.Shinde 等[16]使用混合蒙特卡羅算法模擬等大球在振動下的自發結晶化過程,發現較低振動強度下結晶化只會在局部區域出現而不能實現全局結晶化,而高振動強度時結晶化過程表現為六方最密堆積結構和面心立方結構的競爭.然而現實世界中真實顆粒多是非球形的,非球形顆粒與球體顆粒的堆積性質存在較大的差異.其中一個主要原因是非球形顆粒接觸形式遠比球形顆粒接觸更加復雜,包括面-面、邊-面、邊-邊和頂點-面4 種基本接觸形式[17].這促使人們開始進行關于非球形顆粒堆積性質的研究.

Baker 等[18]通過沉降實驗研究了正四面體、正六面體、正八面體、正十二面體和正二十面體共五種柏拉圖實體的最密隨機堆積(RCP)和最松隨機堆積(random loose packing,RLP)的體積分數,發現除了立方體可以實現無空隙的全空間密堆積外,其他四種實體的RCP 和RLP 體積分數均隨邊數的增加而逐漸下降,實體的摩擦系數越大其RCP 和RLP 的體積分數越低.Donev 等[19]發現不同長短軸的橢球顆粒最密隨機堆積體積分數不盡相同,最高可達0.74,此時橢球平均配位數遠高于球體.Torquato等[20]通過ASC (adaptive shrinking cell)數值模擬算法指出正八面體最密規則堆積的體積分數約為0.947,正十二面體約為0.904,而正二十面體約為0.836,遠高于實驗發現的隨機堆積體積分數.B?rzs?nyi 等[21]通過環剪實驗發現細長棒狀顆粒會自發形成一定取向的規則排列,且同流線之間存在一個特定夾角,該夾角與剪切速率無關.Hidalgo 等[22]通過筒倉中棒狀顆粒沉降實驗發現,顆粒傾向于以不同的傾角在筒倉中形成有序排列,最可幾傾角的大小與顆粒的長徑比有關,其中方形顆粒最易以對角線沿重力方向排列.Asencio 等[23]通過容器往復水平旋轉的方式而不是傳統的振動或者敲擊的方式對圓筒容器中的立方體骰子進行旋轉剪切,實現了立方體顆粒最密規則堆積,為非球形顆粒的堆積研究提供了新思路.

盡管實驗上已經對旋轉圓筒中立方體顆粒的有序堆積的研究取得了重要進展,然而由于所研究顆粒體系的復雜性和控制參數的多樣性,目前對非球形顆粒有序堆積的細致過程和力學機制的理解還不夠深入,需要進一步研究討論.三維顆粒系統內部結構的實驗觀測通常是困難的,其力學行為的問題也難以通過實驗得到完全解決.離散元方法能夠跟蹤到每一個顆粒的空間位置,從而可以記錄內部結構在介觀尺度的細節信息,是對顆粒體系動力學行為實驗研究的有力補充[24-26].因此,本文利用離散元方法對旋轉圓筒容器內立方體顆粒有序堆積過程進行數值模擬以獲取立方體顆粒有序化過程中的結構演變特征,分析了容器運動方式對立方體顆粒有序堆積過程的影響規律,有助于深入理解復雜顆粒系統的結構演化的微觀機理.

1 圓角立方體顆粒有序堆積過程的離散元數值方法

1.1 基于超二次曲面的圓角立方體顆粒

超二次曲面形狀是二次曲面的延伸,80%的常見非球形顆粒幾何形狀可由超二次曲面方程描述[27-28].本文所模擬的立方體顆粒具有高度的對稱性,因此選用超二次曲面連續函數表示.超二次曲面顆粒的形狀表示為

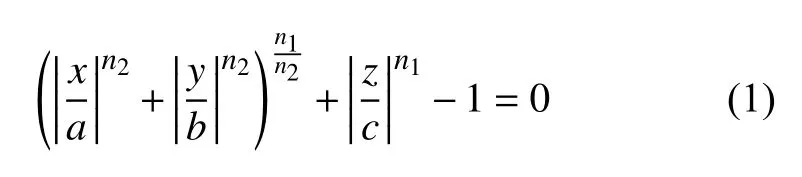
其中,a,b,c分別為顆粒沿主軸方向的半軸長,n1和n2是表征顆粒尖銳度的塊效應參數.通過改變式(1)中表征顆粒形狀的五個形狀參數(a,b,c,n1,n2),可以靈活地獲得不同形狀的顆粒.當 n1=n2=8,a=b=c 時,即可構造帶有較小圓角的立方體顆粒單元.

1.2 圓角立方體顆粒單元間的接觸檢測

顆粒接觸檢測的主要內容是檢測顆粒是否接觸以及確定接觸點和接觸法向.超二次曲面單元間的接觸檢測問題可以考慮為一個定義在全局坐標系下連續且二階可導形狀函數的超二次曲面顆粒間最小距離的最優化問題[25,29-30].最優化問題通過設立拉式算子 λ,由下面的拉式函數給出

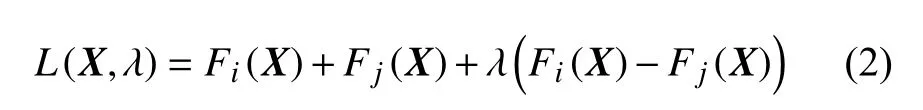
其中 X=(x,y,z)T,最優化問題的解由?X,λL(X,λ)=0確定,引入 μ2=(1-λ)/(1+λ),最終簡化為四元非線性方程組

確定法向重疊量的牛頓迭代公式可寫為

式中,X=X+dX,μ=μ+dμ .計算結果 X0滿足Fi(X0)＜0 且 Fj(X0)＜0 則表明兩個單元間發生接觸.接觸法向 n 可表示為n=?Fi(X0)/||?Fi(X0)|| .進一步考慮Xi=X0+αn 和 Xj=X0+βn,這里未知參數 α 和β 可通過一元非線性牛頓迭代得到:因此,法向重疊量可表述為 δn=Xi-Xj.

1.3 接觸模型及接觸力的計算

基于球體的赫茲接觸模型和橢球體的表面曲率接觸模型,超二次曲面單元的非線性接觸力可按照考慮等效曲率的接觸模型計算[31].在超二次曲面顆粒的相互作用中,顆粒間的相互作用力可認為是法向接觸力和切向接觸力的疊加.法向接觸力主要包括彈性力和黏滯力,此外非球形不規則顆粒的接觸力可能不通過顆粒形心,因此引起的附加彎矩也應被考慮[32].

法向作用力可以表示為

其中,Kn為兩個接觸顆粒間法向有效剛度,δn為兩個接觸顆粒間的法向重疊量,Cn為兩個接觸顆粒間的法向黏性系數,B 為兩個接觸顆粒間的黏滯系數,vn為兩個接觸顆粒間的法向相對速度.

法向有效剛度 Kn和黏滯系數 B 可由顆粒材料的彈性模量 E、泊松比 ν 和接觸點處的平均曲率半徑R 通過下式得到

其中,Ri和 Rj分別表示顆粒 i 和顆粒 j 的等體積球半徑,mi和mj分別表示顆粒 i 和顆粒j 的質量.

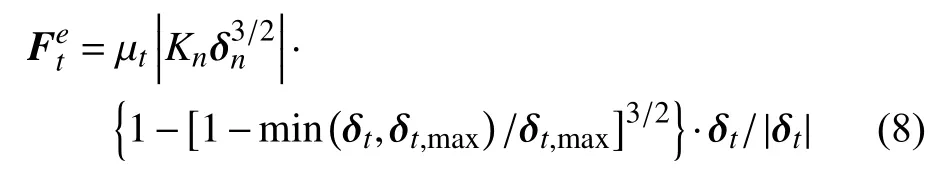
其中,μt為滑動摩擦系數,δt為切向重疊量,

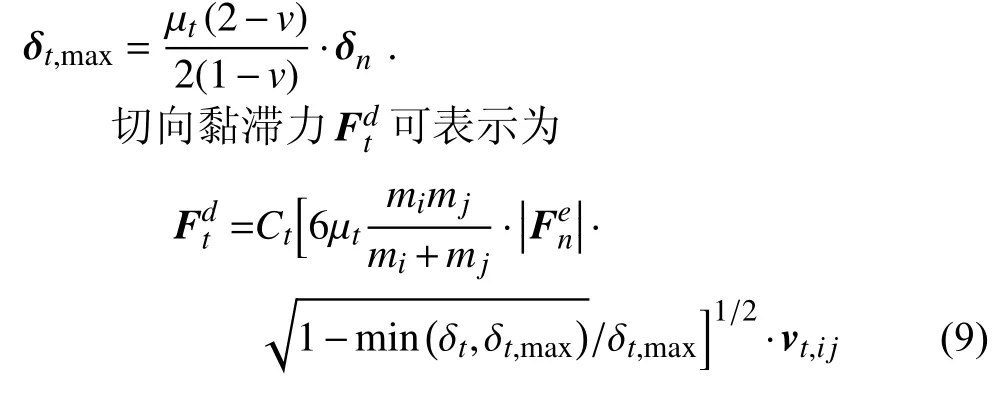
其中,Ct為切向黏滯系數,vt,ij為單元間的切向相對速度.

當顆粒間發生相對轉動時,由滾動摩擦引起的力矩可表示為

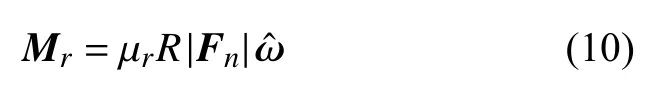
其中,μr為滾動摩擦系數,=ω/|ω| 為接觸顆粒間的單位相對角速度.

1.4 圓角立方體顆粒的運動控制方程

顆粒的運動包括平動和轉動,其平動的控制方程為

其中,mi和 Xci是顆粒i 的質量和顆粒質心的坐標,Fi是作用在顆粒 i 上的合外力.

而顆粒的轉動遵循動量矩定理為

其中,Ii和 ωi分別是顆粒 i 全局坐標下的慣性矩和角速度,Li是顆粒 i 的角動量,Ti是作用在顆粒 i 上對顆粒質心的總轉動力矩.對于非球形顆粒,其慣性矩與顆粒的位向有關,在全局坐標系下,非球形顆粒的慣性矩是一個各個分量都可能不為零的二階張量,運動的描述十分復雜,而在固定于顆粒本身的局部坐標系中,非球形顆粒的主慣性矩是一個僅對角線元素不為零的二階張量,運動描述簡便.因此,引入可以實現局部坐標系和全局坐標系相互轉化的四元數 q 表示顆粒的位向

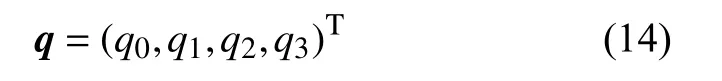
非球形顆粒的位向通常由全局坐標系 eG向固定于顆粒本身的局部坐標系 eL的轉換表示,而四元數q 可以通過轉換矩陣 A 實現這種坐標系之間的相互轉換

這里轉換矩陣滿足 A-1=AT,且由四元數確定

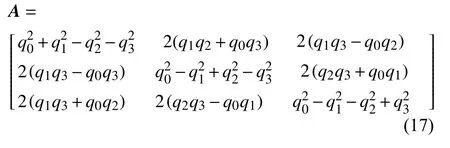
根據建立在角動量定理上的歐拉運動定律可以得到局部坐標系下的顆粒轉動方程

1.5 圓角立方體顆粒有序堆積過程的實施方案

程序中顆粒所處容器為圓柱形轉筒,半徑r=0.067 m,高度h=0.17 m.初始時,800 個邊長為0.01 m 的立方體顆粒在圓筒上方空間生成,之后以一定速度掉落至容器中并等待直至形成位置和取向均隨機的堆積體.通過邊界的“往復旋轉”向立方體顆粒堆積體傳遞邊界轉動產生的剪切作用,如圖1所示.離散元模擬中所需的主要計算參數如表1 所示,模擬環境重力加速度為g=9.81 m/s2.轉筒邊界以一個選定的峰值角速度 ω0進行正反向的循環旋轉,邊界的切向加速度a 為

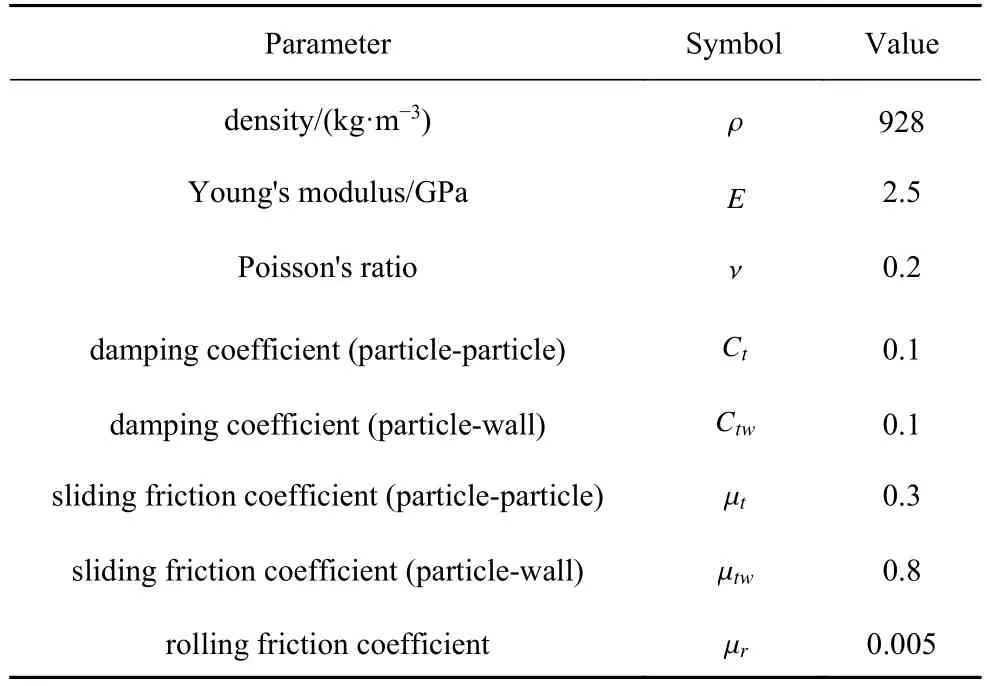
表1 轉動驅動立方體顆粒有序堆積過程的主要計算參數Table 1 DEM simulation parameters of ordering of cubes

圖1 裝置示意圖以及邊界旋轉方式Fig.1 Schematic diagram of simulation and boundary rotation mode

其中R 為圓柱形邊界的半徑,v 是邊界的切向速度,Δt是反轉過程需要的時間.使用重力加速度無量綱化后的扭轉加速度 γ 為

旋轉過程中單向轉動的角位移 β 為

在上述模型和計算條件的基礎上,借助自主開發的GPU 并行離散元計算程序針對立方體顆粒受轉動驅動有序堆積過程進行模擬計算.計算平臺為配備英特爾xeon 4210 CPU 和Nvidia Tesla K40 顯卡的工作站.由于與球體顆粒相比,超二次曲面單元間的接觸判斷更加復雜,其采用非線性牛頓迭代算法經多次迭代才可計算出單元間的重疊量.因此,對于非球形顆粒系統,超二次曲面單元比球形單元具有更低的計算效率和更長的計算時間.由于本文研究所模擬的實驗過程歷時較長,且Asencio 等[23]的實驗系統中顆粒數目(25 000 個)對于模擬而言計算耗費較大,因此選取立方體顆粒總數為800 以觀察其有序堆積現象.

2 結果與討論

2.1 立方體顆粒有序堆積的對比驗證

Asencio 等[23]的實驗證實當圓筒扭轉加速度大于一定值時,圓筒內的立方體顆粒會形成密實有序的堆積體.本文的模擬中也觀察到了類似的結果,如圖1 所示.這里引入兩個統計量表征立方體的有序堆積過程.體積分數 φ (填充率)可以描述顆粒體系的密實狀態.有序度參量 S4通過立方體顆粒的朝向計算得到,用于定量描述立方體顆粒體系的有序化堆積程度.

體積分數 φ 的一般定義為總顆粒的實際體積除以顆粒堆積體占據的空間體積,即

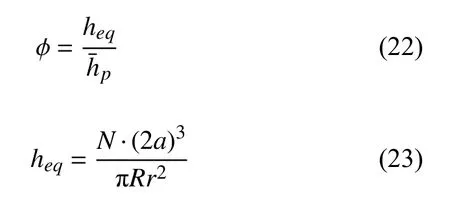
其中,heq是顆粒總體積除以容器底面積得到的等效圓柱體高度,是立方體顆粒堆積體上表面的平均高度.上表面的平均高度的計算方法是將顆粒域劃分為一系列適當大小的網格,標記每列網格中(沿容器高度方向的若干網格稱為一列)位置最高的顆粒的z 坐標,再對所有列位置最高顆粒的z 坐標求平均值并加上顆粒的半邊長修正得到上表面的平均高度式(23)中,N 為顆粒總數,單一顆粒體積按照標準立方體體積計算.其圓角缺失的部分體積根據高斯-勒讓德積分公式計算為標準立方體體積的6%,因此式(23)計算得到的體積分數會略大于真實的體積分數.本文選用式(23)計算體積分數是為了與文獻[23]的體積分數計算方法保持一致,以便于數值模擬結果和實驗結果相對比.

有序度參量 S4[33]為

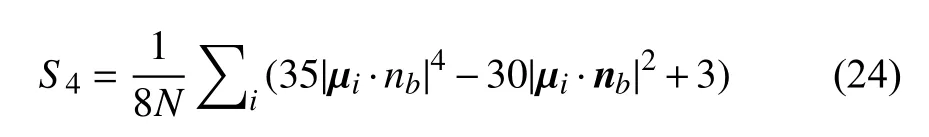
其中 μi為立方體顆粒i 的表面外法線方向,nb=(0,0,1)T為轉筒的轉軸方向.一般的超二次曲面顆粒有三個顆粒主軸,而對于具有良好對稱性的立方體顆粒,三個顆粒主軸無需進行區分.因此,在數值計算模型中,改進的 S4計算公式為

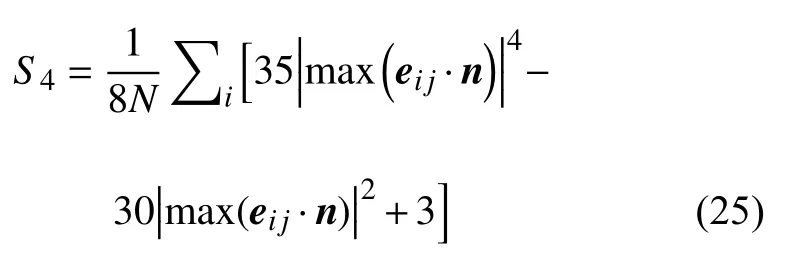
其方中向 向j=量1,.2m,3a;xe(ieji表j·n示b)顆表粒示i的3 個3顆個粒顆主粒軸主的軸單的單位位方向向量分別與 nb點乘的最大值.數值計算模型中,顆粒各主軸方向由四元數確定,因此,顆粒主軸在全局坐標系下的方向向量為

圖2 為 γ=1.01,ω0=5 rad/s 時,φ 和 S4隨旋轉次數的變化.其中圖2(a)為文獻[23]的實驗結果.如圖所示,數值模擬得到的 φ 隨旋轉次數增加的變化趨勢同實驗結果所展示的變化趨勢基本一致,呈現隨著旋轉次數對數值的增加逐漸增大直至穩定的特點.這種變化趨勢與Nowak 等[34]通過敲擊實現球形顆粒隨機堆積體系密實化所發現的 φ 的變化規律完全一致.這意味著對于立方體顆粒,容器的旋轉剪切扮演了敲擊的作用,通過這種簡單的人為設計擾動方案可以得到接近立方體顆粒最密規則堆積的結構.本文所得到的體積分數達到最終穩定狀態時的數值同實驗結果略有差異.本文不同邊界運動條件下的數值模擬最終結果均為一個7 層的立方體顆粒堆積體,最上層內的顆粒約為69～72 個,設置這些顆粒是為了保證下部6 層的顆粒數量達到飽和,其他各層顆粒約為119～123 個.若去掉最上層顆粒,φ 的值約為0.88.由于正方體邊長去貼合容器邊壁時難免有空隙且模擬計算的顆粒數小于實驗體系,這也使模擬所得到的 φ 略低于實驗值0.96.此外模擬得到的 φ 達到穩定狀態后漲落相較實驗結果更為明顯.這是因為當第六層顆粒填滿后,下面六層的排布結構就不再顯著地變化,但是最上層的顆粒還會伴隨下層顆粒的整體轉動產生移動和翻轉,對于體積分數的計算結果帶來一定的漲落.如果去掉第七層顆粒,體積分數的漲落是非常小的.

圖2 體積分數及有序度隨旋轉次數的變化Fig.2 Packing fraction Φ and cubatic order parameter S4 versus number of rotation

有序度參量 S4隨旋轉次數增加而呈現的變化趨勢與 φ 的變化趨勢相同.S4最終穩定在0.95 左右,標志著體系完成了從無序向有序的轉變.圖中 S4的變化存在一個比較明顯的轉折點,可以定義一個特征旋轉次數 Nr,用于標記體系何時完成有序堆積.相較于實驗結果,模擬計算得到的 Nr小一到兩個量級,可以認為這是由于離散元模擬所用的顆粒數遠小于實驗顆粒數目所導致的.數值模擬選取的容器底面直徑和顆粒邊長比為13.4,而實驗中容器底面直徑和顆粒邊長比約為35.下一小節中,可以清楚地看到,邊壁的旋轉剪切作用所導致的顆粒體系的密實有序化過程是逐漸的從外側向內側演化發展的.模擬僅需要完成4～5 層的顆粒同心圓排列就基本完成有序化過程,而實驗則需要完成15 層左右的同心圓排列.考慮到往復旋轉邊界的擾動影響必然是通過最靠近筒壁的顆粒逐漸向內部傳遞,因此模擬結果得到的Nr小于實驗結果是可以理解的.盡管如此,模擬得到的 φ 和 S4的變化趨勢,可以很好地反映立方體顆粒在邊界往復旋轉作用下的密實化效果和有序化過程,這表明基于超二次曲面顆粒單元的DEM 數值模型的有效性.

2.2 立方體顆粒有序堆積過程的結構演化

圖3 給出了 γ=4.04,ω0=10 rad/s 時,立方體顆粒堆積體在側面、半剖面以及底面視角下的有序化過程.如圖所示,初始時刻體系處于隨機堆積的狀態有序度較低,底面上顆粒分布相對松散.隨著旋轉剪切次數的增加,幾十轉內位于頂層的顆粒(藍色)會不斷的通過縫隙掉落至下層顆粒(紅色)中,體系將迅速完成主要的密實化過程.同時,靠近底面和容器邊壁的顆粒呈現某一面平行容器底面的有序狀態,而靠近轉軸的內部顆粒則依然處于無序的狀態.之后的幾百轉內,最低的6 層顆粒逐漸填滿并全部實現某一面平行容器底面的有序排列,最上一層顆粒則依然會出現移動和翻轉.從底面層顆粒的速度分布(彩圖)可以看出,最靠近容器邊壁的一圈顆粒速度最大,越靠近轉軸的顆粒速度越小,顆粒間的速度差會造成顆粒間的切向滑動摩擦力.這證明邊壁擾動確實是以摩擦力的形式促使顆粒的有序堆積從靠近筒壁的顆粒逐漸向內演化.

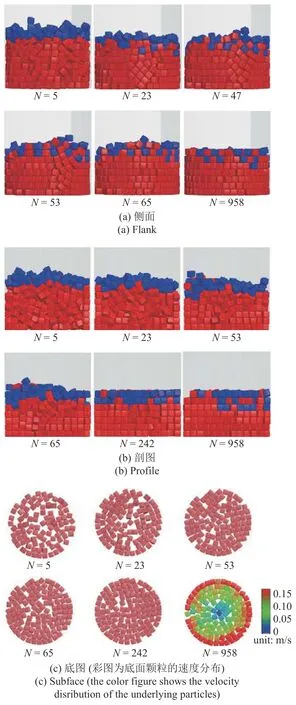
圖3 立方體顆粒的有序化過程Fig.3 The ordering process of cubic particles

進一步地細致觀察發現初始時刻立方體顆粒完成沉降堆積后,雖然整體的有序度比較低,但是單一顆粒和其相鄰顆粒間并不會存在巨大的取向差異.Boton 等[35]研究結果表明,具有平面的非球形顆粒相互接觸時,面與面的接觸方式最大程度阻礙顆粒的轉動且最容易滿足顆粒堆積體的穩定性要求,因此具有平面的規則非球形顆粒很容易形成特定方向的排列,對于具有高度對稱性的立方體顆粒更是如此.Bautista-Carbajal[36]給出了二維狹縫中方形顆粒的團簇相圖,結果表明狹縫中的方形顆粒有三種穩定的狀態,分別是邊長平行狹縫邊界,對角線垂直狹縫邊界以及兩者的混合狀態.對于三維立方體顆粒,Zuriguel 和Maza 等[22,37-38]系列工作表明方形顆粒在容器中的沉降極易形成面對角線沿重力方向(邊與水平面夾角45°)的團簇.這一特性可以通過平均場近似解釋.力鏈穿過給定粒子的概率應與其側面在水平方向上的相對投影成正比,方形顆粒在這一角度下力鏈的穿透概率取極大值,此時顆粒體系內部的沿重力方向的力鏈分布最接近高斯分布狀態,顆粒間具有最大的接觸面積.從側視圖可以看出,在圓筒邊壁最初的幾十轉內,重力誘導顆粒迅速的掉落,容易形成由幾個或者幾十個顆粒組成的面對角線沿重力方向的團簇.后續邊壁的往復旋轉則是誘導這些團簇整體轉動形成立方體顆粒某一面平行容器底面的團簇.文獻[23]認為重力因素和邊壁旋轉因素對顆粒團簇的最終形態構成競爭關系.當旋轉擾動強度足夠劇烈時,團簇會以整體旋轉的形式完成排列取向的轉變.當旋轉擾動強度較低時,體系最終為面對角線沿重力方向的顆粒團簇和某一面平行容器底面的顆粒團簇共存的狀態,例如圖4 內插圖所示結構,此時 S4穩定在0.82 左右.

圖4 γ 一定,不同峰值角速度 ω0 下,填充率 Φ 和有序度參量 S 4 的變化Fig.4 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for γ=1.01 and differentω0

2.3 立方體顆粒有序堆積的影響因素

Asencio 等[23]認為每次旋轉時,對顆粒體系施加的 γ 對立方體顆粒的有序堆積起決定性的作用.如果 γ 大于0.5,那么立方體骰子必然能在容器約10 萬次的往復旋轉后達到有序堆積狀態.此時每一層的立方體顆粒都排列成幾乎完美的同心環.相反,如果 γ 低于0.5,那么有序堆積的速度就會變得非常緩慢,以至于很難判斷顆粒是否最終能達到最密堆積狀態.即使經過10 萬次的旋轉,靠近圓柱體中心的顆粒仍然處于高度混亂的狀態.本文的模擬方案中,容器 γ 由 ω0和反轉時間 Δt 決定.不同的 ω0和Δt可能對應相同的γ .因此設計了一組 γ 相同但 ω0不同的容器運動條件,考察立方體顆粒的有序堆積過程,如圖4 所示.如果 γ 是立方體顆粒有序堆積的控制變量,那么可以預期只要 γ相同,盡管 ω0不同,容器各運動條件下顆粒有序堆積過程應該是幾乎相同的.但是模擬結果顯示 γ 一定時,隨著 ω0的增大(相應的反轉時間 Δt 增加),顆粒體系只需更少的往復旋轉次數就可達到最密實狀態并完成顆粒的有序排列.應當指出,ω0=2.50 rad/s的這組模擬,當往復旋轉次數達到4000 次時仍未完成完全的有序化轉變(有序度參數 S4約為0.82),這是因為靠近容器邊壁的部分顆粒形成面對角線沿重力方向的團簇,如圖4 內插圖所示.無法確定更多的往復旋轉次數是否一定能實現所有顆粒均為某一面平行水平面的有序排列.這種情況與文獻[23]報道的低于0.5 時的旋轉剪切結果類似,容器內兩種取向的團簇顆粒共存.這意味著立方體顆粒通過邊界的剪切作用完成有序堆積確實需要外界給予的擾動強度達到一定的值,但將作為衡量擾動強弱的指標并不完備,模擬結果顯示這個強度指標與 ω0和Δt 有關.

為了進一步研究 ω0和 Δt 對立方體顆粒有序堆積過程的影響,首先設計了一組 ω0相同但 γ 不同的容器運動條件,模擬結果如圖5 所示.ω0一定時,隨著的 γ 增大,立方體顆粒需要更多的往復旋轉次數才能達到最密實狀態并完成顆粒的有序化轉變.γ 對顆粒的密實化和有序化呈現消極影響,這一結果與文獻[23]矛盾.同時設計了一組 Δt 相同但 ω0不同的運動方案,此時隨ω0的增加 γ等比例增大,如圖6 所示.結果顯示更高的 γ 下立方體顆粒確實僅需要更少的往復旋轉次數就可以完成顆粒的密實化和有序排列,這一結果與文獻[23]一致.文獻[23]并未給出轉筒詳細的工作條件,但提及到實驗采用的轉筒僅在反轉時對顆粒有剪切作用.可以認為實驗中容器的運動模式接近為方波形式,角速度反向所需要的時間可能為定值,如此 γ 的增大完全由峰值角速度的增大所導致,類似圖6 結果所對應的運動方案.

圖5 角速度 ω0 一定,不同 γ 下,填充率 Φ 和有序度參量 S 4 的變化Fig.5 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for ω0=5.0 rad/s and differentγ

圖6 反轉時間一定,不同 γ 下,填充率 Φ 和有序度參量 S 4 的變化Fig.6 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for the constant inversion time and differentγ

綜合以上結果,本文提出用容器的旋轉角位移β作為衡量擾動強弱的指標更為合理.圖7 給出了旋轉角位移 β 和特征旋轉次數 Nr的關系,圖中所有模擬組的 S4最終的穩定值均大于0.94,可認為體系完成了有序堆積.對 β 與 Nr繪制雙對數散點圖并進行線性回歸,得到 β 與 Nr之間的關系為

圖7 特征旋轉次數與旋轉角位移的關系Fig.7 Characteristics rotation number versus angular displacement

考慮到實驗誤差,可以認為 Nr和 β 之間為簡單的反比例關系即

其中 Nr0為系數取決于顆粒體系的數量,容器能容納的單層顆粒越多則 Nr0越大.利用這種反比例關系,很容易理解模擬中發現的S4曲線重合的現象.比如邊界 γ=1.01,ω0=5 rad/s 和 γ=4.04,ω0=10 rad/s 的兩個邊界運動方案,對應的旋轉角位移均為0.338 rad,因此兩者的 Nr幾乎完全相同,如圖8 所示.

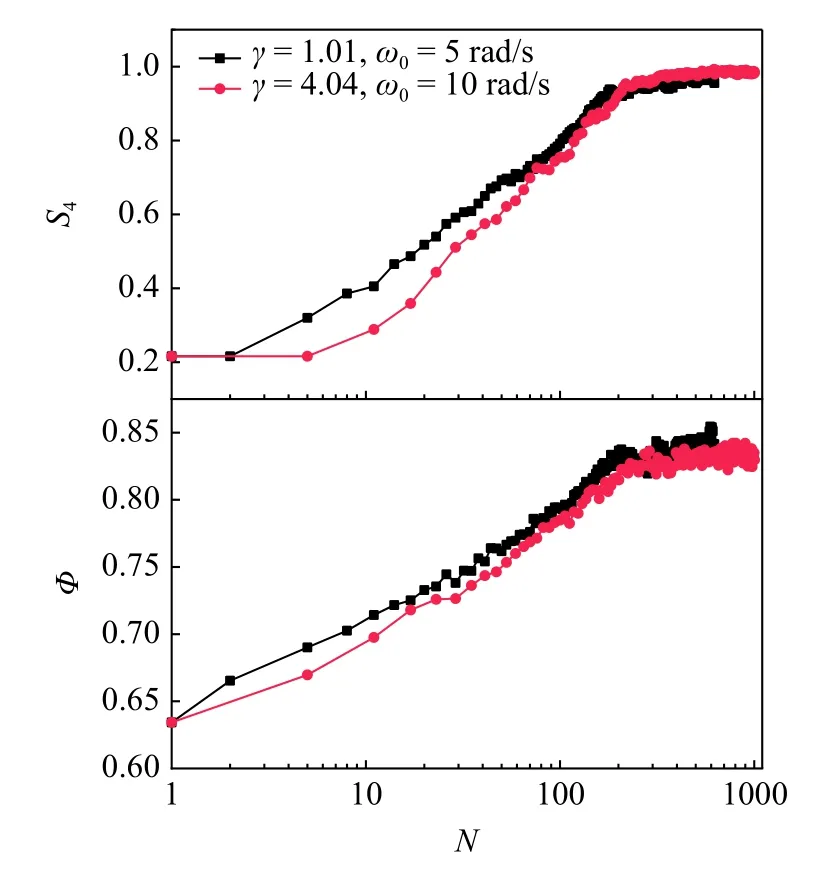
圖8 相同 β 值下,填充率 Φ 和有序度參量 S 4 的變化曲線.Fig.8 Volume fraction Φ and cubatic order parameter S4 versus number of rotation N for the constantβ

這種反比例關系是因為,容器旋轉擾動作為類似熱漲落的驅動力,提供了立方體顆粒有序堆積的能量.考慮圓形底面的對稱性,可以近似將所有顆粒受到的來自邊界的摩擦力簡化為對全體顆粒的力偶,單次旋轉時邊界對顆粒體系做功等于力偶矩乘以旋轉角位移.旋轉角位移越大,容器邊界輸入能量越多,顆粒越容易產生運動,直至完成有序排列,此時體系的勢能最低,顆粒單元與相鄰顆粒間的面-面接觸約束最強烈.當然式(28)的適用范圍一定存在上下限.對于適用上限可以合理想象即使旋轉角位移非常大,但是完成有序堆積依然需要一定次數的往復旋轉而不僅僅是一兩次的旋轉.對于適用下限上文已經闡述當旋轉角位移小于某一臨界值時,體系最終會形成兩種形式的團簇顆粒共存的結構,只是下限的臨界值所對應的力學機理有待進一步研究.

2.4 不同重力加速度下的立方體顆粒剪切排序

深空環境中,固體星球表面聚集著大量的顆粒物質.人類對于深空環境下顆粒物質的物理規律和操控方式的認知仍比較淺顯.比如太陽系中大行星表面的風化層典型顆粒粒徑小于小行星表面風化層的典型顆粒粒徑,即使是這樣簡單的現象,人們對于其物理機制的認知尚未完全統一.深空環境的顆粒堆積問題亦是如此.為研究重力加速度對立方體顆粒受轉動驅動實現有序堆積的影響,設計了三種不同重力加速度下(地球、火星和月球的重力加速度)的邊界運動條件.鑒于顆粒物質具有非線性和對微小作用力敏感的特性,初始堆積狀態將影響后續堆積演變特征,所以本文三種重力加速度下的顆粒堆積結構保持不變.且同時保持 γ=4.04,ω0=10 rad/s 不變,模擬結果如圖9 所示.地球和火星的重力加速度下,立方體顆粒都實現了無序向有序的轉變并達到了最密堆積和完全有序狀態,但火星重力加速度下達到有序狀態需要的往復旋轉次數更多.而月球重力加速度下顆粒體系雖然 φ 和 S4也隨著邊界不斷旋轉而變大,但無法達到完全有序和最密實狀態.上述結果表明,亞重力加速度條件下,容器的往復旋轉依然是實現立方體顆粒有序堆積的有效方式,但重力加速度的減少會對立方體顆粒的有序堆積過程產生抑制效果.這是因為隨著重力加速度的減小,顆粒間的摩擦力相應減小,不利于顆粒受到擾動后尋找下沉路徑.本文也曾嘗試過模擬十分之一地球重力加速度以及更低重力加速度條件下的立方體顆粒有序堆積過程,但上層顆粒極容易形成類似顆粒氣體的漂浮狀態,無法再將其視為一個類似固體的堆積體.

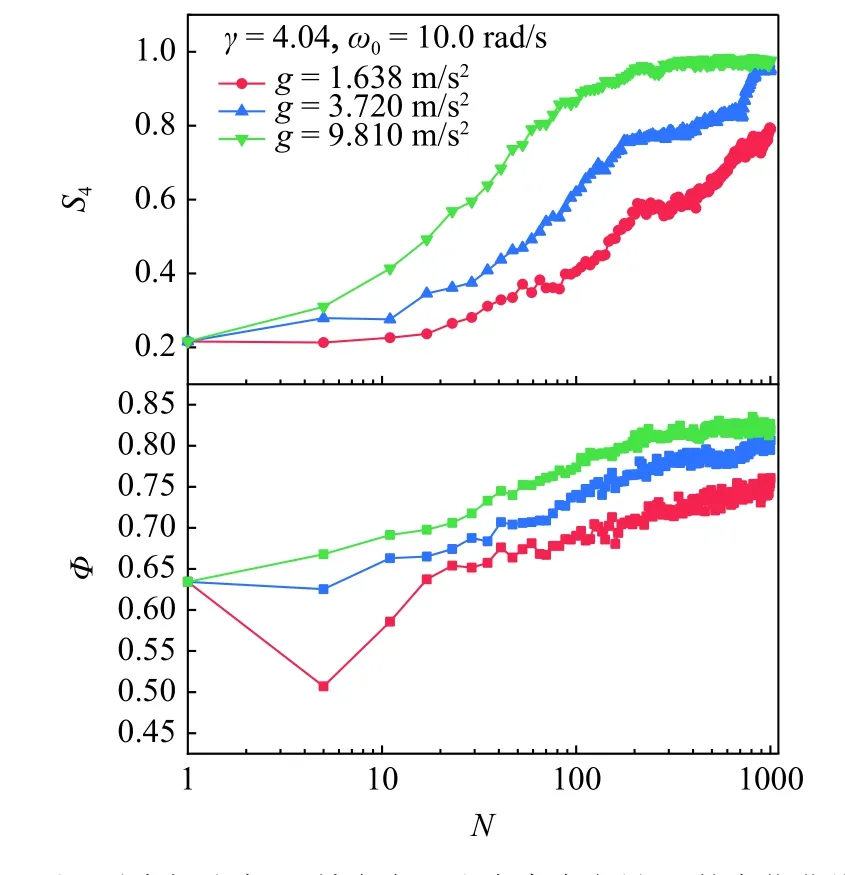
圖9 不同重力加速度下,填充率 Φ 和有序度參量 S4 的變化曲線(模擬參數:邊界 γ=4.04,峰值角速度 ω0=10.0 rad/s)Fig.9 Volume fraction Φ and order parameter S4 versus number of rotation N for different acceleration of gravity (γ=4.04,ω0=10.0 rad/s)

3 結論

基于超二次曲面方程構建立方體顆粒形態,采用離散元方法針對圓筒內隨機堆積立方體顆粒在容器邊界往復旋轉作用下的有序化堆積行為開展數值模擬研究,復現了實驗中觀察到的立方體顆粒實現最密規則堆積的過程.通過本文研究,得到如下結論.

(1)立方體顆粒系統的體積分數和有序度隨著容器往復旋轉次數增加而逐漸增大直至穩定.顆粒系統的有序堆積過程表現為由外層顆粒向內部顆粒逐漸擴展的演化趨勢.

(2)容器旋轉角位移是立方體顆粒實現有序堆積過程的控制變量.顆粒完成有序堆積過程所需的特征旋轉次數與容器旋轉角位移呈現反比例關系.旋轉角位移過低,體系只會形成某一面平行水平面的顆粒團簇與面對角線平行重力的顆粒團簇共存的結構.

(3)在亞重力環境下立方體顆粒同樣可以通過容器的往復旋轉實現最密規則堆積.重力加速度的減少會抑制立方體顆粒從無序堆積向有序堆積的轉變.

致謝

本項目承蒙中國載人航天工程國際合作項目支持.