宏觀交通流模型的余維2 分岔分析1)

范爽爽 劉丹陽 段利霞,

* (北方工業大學電氣與控制工程學院,北京 100144)

? (北京理工大學自動化學院,北京 100081)

** (北方工業大學理學院,北京 100144)

引言

交通擁堵問題一直以來都是學者關注的主要問題.現有的解決方案仍有不足,原因之一是運輸系統的復雜性,所有方面都很難集成到一個解決方案中.目前,人們從不同角度建立了各種交通模型來解釋交通擁堵的復雜結構[1-6].一般而言,現有的交通流模型可分為4 類:元胞自動機模型[7]、氣體動力學模型[8]、水動力學模型[9]和最優速度模型(OVM)[10].OVM 是最著名的跟車模型之一,受OVM 的啟發,提出了許多考慮其他交通因素的跟車模型[11-13].Jiang 等[14]提出了一個全速差模型(FVDM),它描述了擁擠流和均勻流,對于低密度實現均勻流,在一定臨界密度上變得不穩定,出現擁擠流.在臨界密度下,該模型預測了汽車密度和交通流量之間存在不連續性.駕駛員記憶在駕駛中不可缺少,考慮記憶效應的跟車模型表明,歷史信息將有助于提高交通流的穩定性[15-18].一些學者研究了交通流模型中速度和車頭時距隨記憶的變化[19].數值模擬表明,駕駛員的記憶對交通行為和穩定性有顯著的積極影響[20].在實際交通環境中,最優速度隨記憶的變化可以預測下一時刻加速度的變化.與那些不熟練的駕駛員相比.熟練的駕駛員對最優速度的預期和最優速度變化的記憶能力會有更快的反應.然而,對連續模型上的駕駛員記憶的調查是罕見的.為了克服這一局限性,并受到記憶效應的啟發,本文將提出一個改進的連續模型來研究交通流的最優速度隨記憶變化.

相平面分析已經被證明是分析復雜交通流現象的一種合適工具[21].Kuhne 等[22]在黏性高階模型中預測了Hopf 分岔、孤立波和周期振蕩解,提出了雙穩定性情況,并解釋了擁擠流的時滯現象.Lee 等[23]解釋了在所謂的慣性跟車模型中極限環機制.最近,Saavedra 和Velasco[24]采用了數值方法,結果與Lee 的理論分析結果一致.

現有的交通流理論及其求解方法存在一定的缺陷.例如,目前的建模研究大多集中在均勻交通流上,分析范圍僅限于平衡狀態的小范圍擾動,缺乏對交通流的全局分析[25-26].因此,反映實際交通流特征的交通流理論值得進一步研究.分岔是指由于非線性動態系統的參數跨越一定的閾值,系統的拓撲結構發生明顯變化的現象.大多數交通流模型都是具有參數的非線性方程,當模型中的某些參數發生變化時,交通流量系統的穩定性發生了顯著的變化,這與分岔的定義一致.Kuhne 等[27]將混沌動力學理論應用到Payne 模型中,其結果表明,通過改變瓶頸處的密度和通行能力兩個控制參數,可以改變交通流的狀態,產生亞臨界或超臨界分岔.Li[28]推導出Payne 模型的離散形式,研究了該模型的倍周期分岔現象,發現分岔點的出現會導致交通流模式從自由流改為同步流,混沌現象會導致交通擁堵.一些學者總結了國內外分岔理論的發展[29-30].周偉等[31]通過跟車模型分析了交通流中存在的倍周期分岔和混沌現象.凌代儉和肖鵬等[32]通過非線性時滯跟車模型,證明了系統的穩定性和Hopf 分岔,描述了跟車模型中復雜的非線性現象.Carrillo 等[33]通過嚴格的數學推導發,在一定條件下Bogdanov-Takens (BT) 分岔出現在雙參數動力系統(即二階Kerner-Konhauser(K-K) 模型[34]).Delgado 等[35]證明了K-K 模型中存在退化的BT 分岔,從而解釋了Hopf 分岔和Bautin分岔的存在性.Delgado 等[35]從理論角度證明了宏觀交通流模型分岔的存在性,但分岔引起的具體交通現象不足.為了詳細描述由分岔引起的交通流現象,艾文歡等[36]推導了速度梯度模型中Hopf 分岔和鞍結分岔的存在條件,并繪制了以分岔點為起點的密度演化圖,根據Hopf 分岔理論解釋了交通流的啟停現象.Ren 等[37-39]都做了Hopf 分岔研究,并通過行波參數找到Hopf 分岔范圍,解釋了走走停停現象.但是其他參數的改變也會出現啟停現象,目前很少有人研究其他參數對啟停現象的影響.因此,本文從雙參數分岔的角度分析交通流的Hopf 分岔機制以及相應的交通現象.

本文基于宏觀交通流模型,采用雙參數分岔方法,從全局的角度來分析交通現象.該模型重現高速公路上觀測到的許多復雜的非線性動力學現象,如走走停停波和局部簇.首先,利用變量代換將模型轉換為一個適合于分岔分析的新模型.然后,推導了模型中鞍結分岔存在的條件,得到不同兩參數間的雙參數分岔結構,并對分岔曲線進行分析.最后,利用雙參數分岔區域得到不同單參數分岔結構,通過相平面分析描述和預測高速公路上的非線性交通現象.

1 跟車模型的提出及改進

1.1 宏觀交通流模型

提出了一種考慮最優速度隨記憶變化的跟車模型[40]

其中,xn(t) 是在時間 t 時刻第 n 輛車的位置,?νn表示兩個相鄰車輛的速度差,?xn=xn+1-xn是車頭間距,V(?xn(t))為優化速度函數.V(?xn(t))-V(?xn(t-δ)) 是駕駛員將當前最優速度調整到記憶為 t-δ 時的最優速度,其中,δ 表示記憶步長.a 是敏感系數,λ 為速度差響應系數,γ 是駕駛員最優速度差的靈敏系數.當γ=0或者 δ=0,系統 (1) 就是FVDM 模型.

通過簡單的Taylor 展開,優化速度函數可以寫為

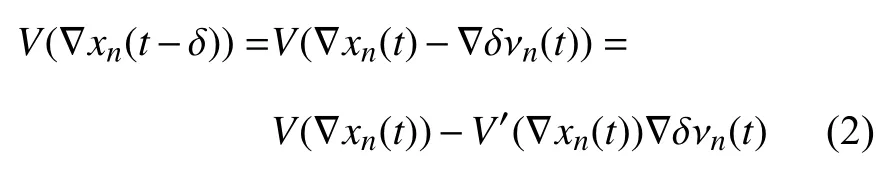
把式(2) 代入式(1),可以推導出

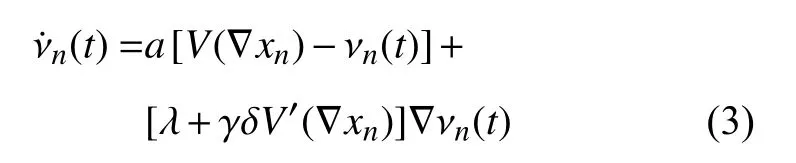
微觀變量轉化為宏觀變量的方法如下

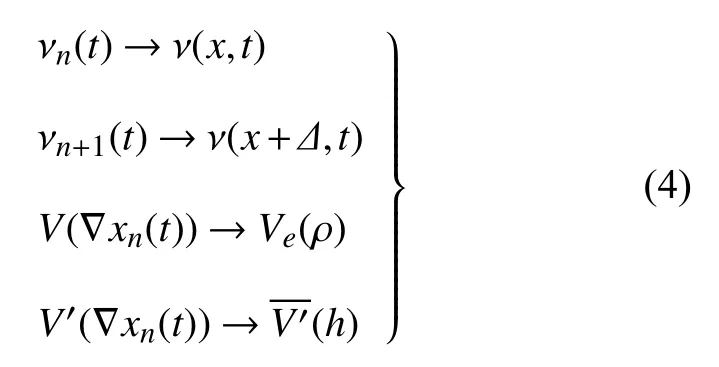
其中 Δ 表示相鄰兩車之間的距離,ρ(x,t) 和 ν(x,t) 分別表示宏觀密度和速度.密度與位置的關系為Ve(ρ) 表示最優速度,

最優速度函數 Ve(ρ) 選擇如下形式[34]

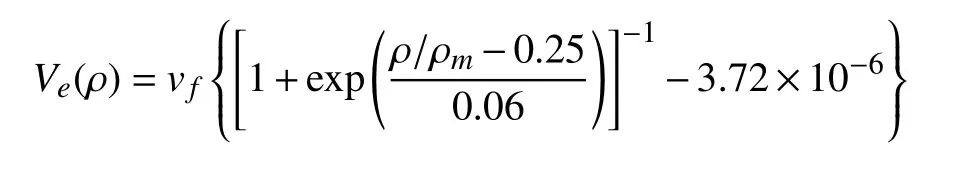
對 ν(x+Δ,t) Taylor 級數展開且忽略高階項,可以推導為

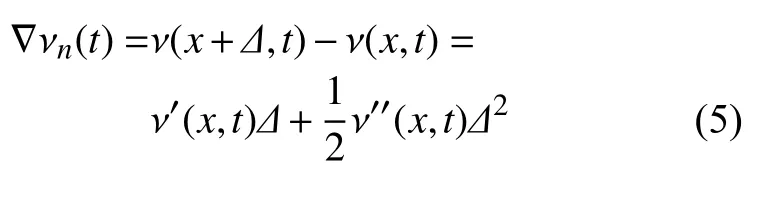
將式(4)和式(5)代入式(3),跟車模型中微觀變量轉成宏觀變量如下

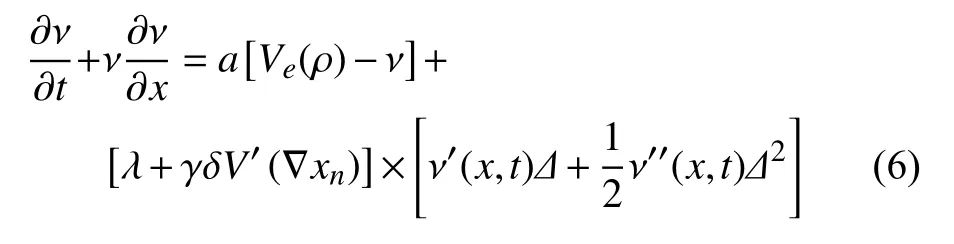
式(6)可以整理為

將流量守恒方程與式(7)結合,將推導出最優速度隨記憶變化的宏觀交通流模型

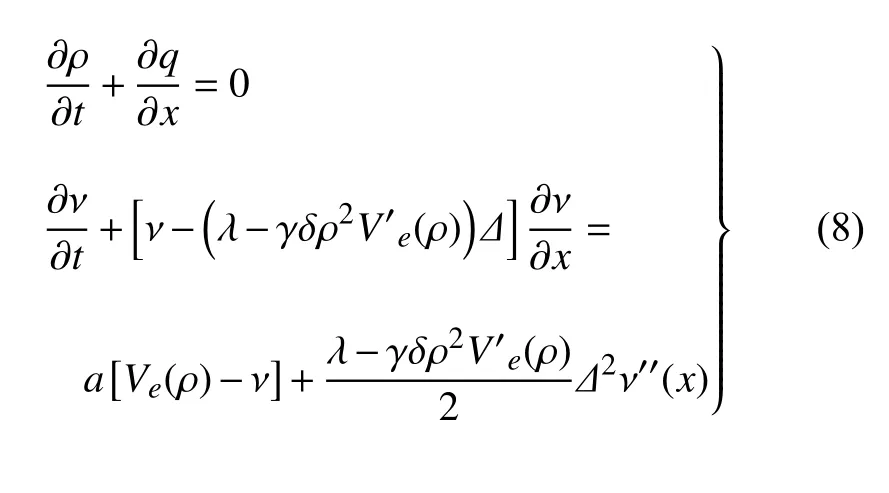
1.2 交通流的行波解

為了研究系統的穩定性,引入了行波解 z=x-ct,將其代入式(8),可以推導出

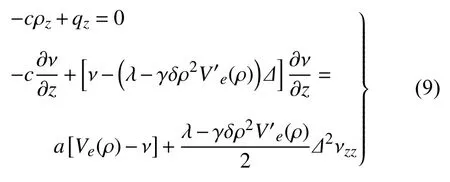
其中交通流是密度與速度的乘積,為 q=ρν .根據式(9)的流量守恒方程,可以得出

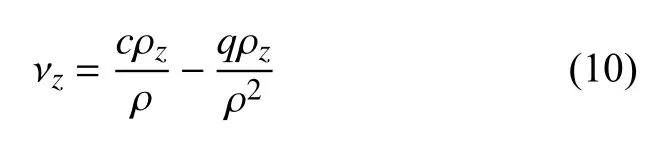
對式(10)等號兩邊分別求導有

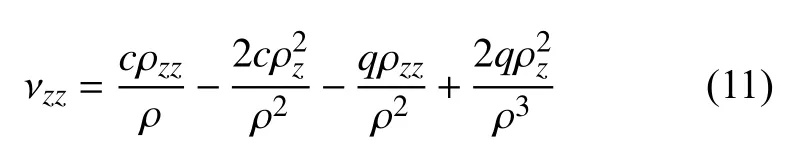
對式(9)的流量守恒方程積分有

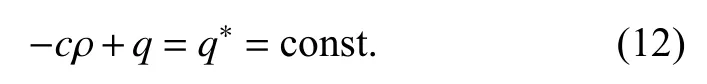
式(9)的動力方程展開為

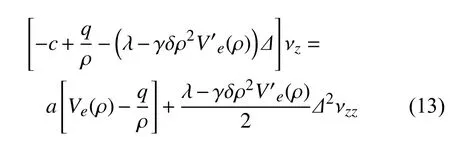
將式(10)和式(11)代入式(13)有

簡化式(15),可以重寫為

在式(18)中,η 和ρ 具有相同的單調性.密度ρ越接近擁擠密度 ρm,則變量 η 趨于無窮,且 y 是 η 的變化率.因此,可以用 η 的軌跡清晰地描述交通擁堵與系統不穩定性之間的關系,從而可將交通流問題轉化為系統的穩定性問題.

2 余維2 分岔分析

系統式(18)的穩定性,即交通流的穩定性,與道路中的小擾動對交通流狀態的影響密切相關.如若系統穩定,那么小擾動在傳播中會逐漸減小,此時車輛暢行;而若系統不穩定,那么小擾動會向上游傳播,此時將逐漸演化為交通擁堵.雙參數分岔能整體分析參數變化和車輛穩定范圍.本文主要研究記憶參數 γ 和行波參數 q*變化時,交通流狀態的轉變.

2.1 鞍結分岔存在條件

引理2.1 (文獻[36]) 考慮系統 x˙=f(x,λ),x ∈Rn,λ ∈R,其中 λ 是一個變量.如果 (x0,λ) 滿足平衡條件假設 ψ 和φ分別為 L 的左右特征向量,就有ψ L=0 和 Lφ=0 成立.當滿足以下條件時,系統在 λ=λ0處存在鞍結分岔

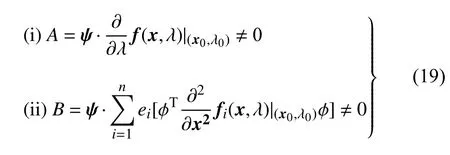
對系統 (18),令 q*作為可變參數,(η0,0) 表示平衡點.在此平衡點處的Jacobi 矩陣可表示為

因為平衡點滿足平衡條件 y=0 和 F(η,δ)=0,因此平衡點處的Jacobi 矩陣為

1-ρmη0=0成立當且僅當 ρ=0,但這是一個平凡平衡點,可以忽略不計.此外,變量 η 永遠不能等于0,所以有 A ≠0 成立.

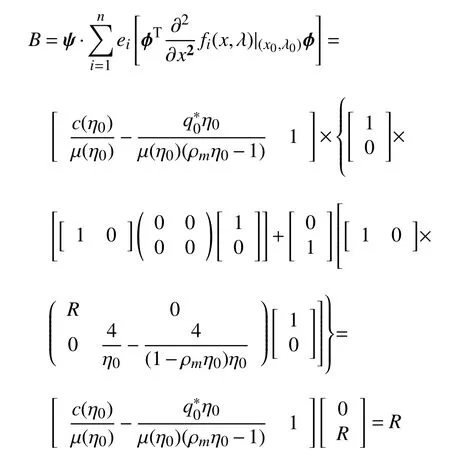
其中

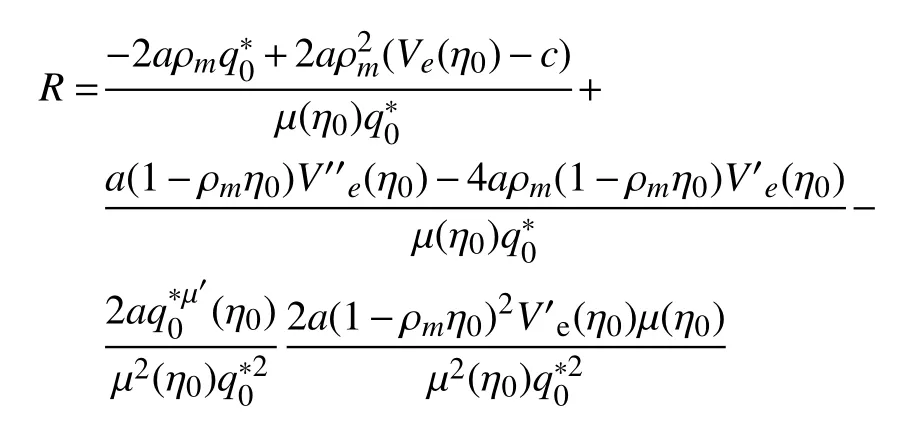
2.2 γ 和 q* 雙參數分岔

當行波參數 q*和記憶系數γ 變化時,交通流會出現穩定、擁堵、走走停停和幽靈擁堵等復雜的交通現象.交通狀態的轉變可能由分岔的類型,以及分岔曲線的相對位置等因素變化引起.下文通過雙參數分岔來研究交通狀態在不同分岔結構下的特征.將行波參數 q*作為第一個分岔參數,即當 q*變化時交通狀態發生變化.將記憶敏感系數 γ 作為次要控制參數,并研究不同 γ 值對交通流的影響.取行波參數 q*＞0,記憶系數 γ ＞0 .當 c=-8.081 veh/s 時,其余參數不變,得到 γ 和 q*雙參數分岔結構如圖1 所示.

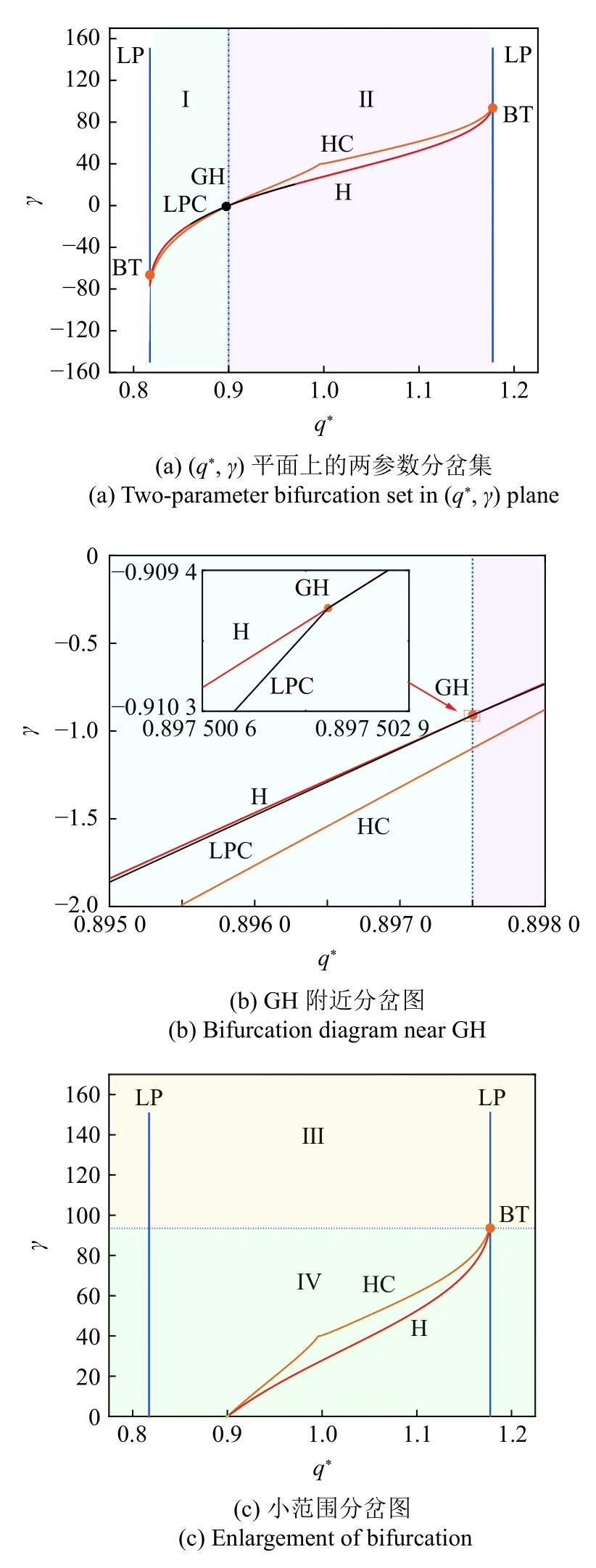
圖1 q* 和 γ 的雙參數分岔Fig.1 Two-parameter bifurcation of q* andγ

圖1(a) 和圖1(c) 中有兩條LP 表示平衡點的鞍結分岔曲線 (藍色實線),由鞍點和結點相遇產生.曲線HC 是同宿軌分岔,鞍點與極限環相遇產生 (橙色實線);H 曲線是Hopf 分岔,焦點的穩定性發生改變(紅色實線);LPC 曲線是極限環上的鞍結分岔,與Hopf 曲線幾乎重合(黑色實線);BT 點表示余維2 Bogdanov-Takens 分岔,是HC,H,LP 3 條曲線的交匯點;GH 點表示余維2 廣義Hopf 分岔,是超臨界和亞臨界Hopf 分岔的臨界點.GH 點附近的結構如圖1(b) 所示.由于 γ ＞0,則系統有效雙參數區域如圖1(c) 所示.GH 點的坐標為 (0.9,1.297 694 5×10-7),γ值幾乎趨于0,將雙參數分岔區域分為Ⅰ和Ⅱ兩部分,如圖1(a) 所示.BT 的坐標為 (1.177 465,97.492 181),將雙參分岔區域分為Ⅲ和Ⅳ兩部分,如圖1(c) 所示.顯然,在區域Ⅳ中分岔結構更豐富,第4 節中將分析參數在不同區域時系統表現的動力學行為對交通現象的影響.

2.3 c 和 q* 雙參數分岔

當行波參數 q*和行波速度 c 變化時,交通流會出現不同的狀態.將行波參數 q*作為第一個分岔參數,行波速度 c 作為次要控制參數,取行波參數 q*＞0,行波速度 c ＜0,克服了許多高階連續模型的反向傳播問題.當 γ=0.5 s-1,q*=0.901 veh/s 時,其余參數不變,得到 c 和 q*雙參數分岔結構如圖2 所示.

圖2(a) 中兩條LP 曲線 (紅色實線) 交于CP 點,產生尖點分岔;HC 是同宿軌分岔 (橙色實線),H 曲線是Hopf 分岔 (綠色實線),兩個余維2 Bogdanov-Takens 分岔點分別交于同宿軌分岔、Hopf 分岔、鞍結分岔交匯處,如圖2(b) 所示.根據BT 與CP 點,將圖2(a) 分成4 個區域.

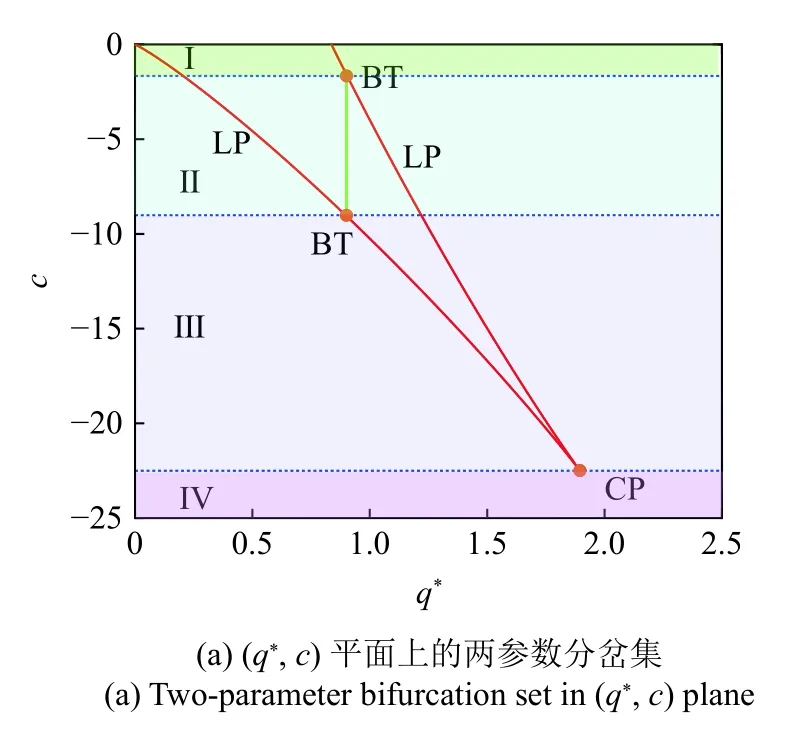
圖2 q* 和 c 的雙參數分岔Fig.2 Two-parameter bifurcation of q* andc

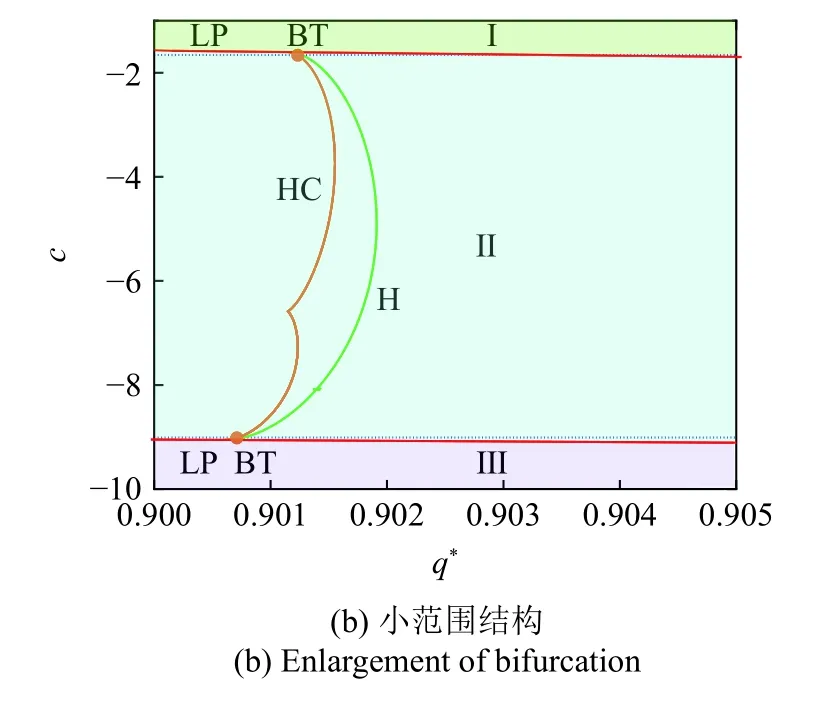
圖2 q* 和 c 的雙參數分岔(續)Fig.2 Two-parameter bifurcation of q* and c (continued)

本節參數取值與3.2 節相同.由于分岔參數不同,得到的分岔結構和分岔曲線完全不同,說明不同的參數對交通狀態可能會有很大的影響.因此本文研究其他參數對交通狀態的影響,是非常必要的.在同一組參數值下,任意兩參數可以兩兩組合,得到不同的雙參數分岔結構.各參數間相互影響,產生不同的交通現象.本文只將行波參數 q*和記憶系數 γ 對交通狀態的影響做詳細的分析.

3 非線性動力學分析

3.1 關于 q* 單參數分岔結構

根據不同分岔結構,圖1(b) 分成兩個分岔區域,分別在不同區域取值,研究關于 γ 的單參數分岔結構,如圖3 所示.

隨著 γ 值減少,q*的分岔結構也發生了變化.當γ=100時 (即在圖1(b) 的區域Ⅲ內) 有兩個鞍結分岔 (LP) 產生,如圖3(a) 所示.綠色實線代表穩定的焦點,當施加小擾動時,密度振蕩且振幅變得越來越小,最終穩定在焦點;紅色虛線表示鞍點,當施加小擾動時,密度有波動,最后穩定.當 γ=30 時 (即在圖1(c) 的區域Ⅳ內) 有兩個鞍結分岔和一個Hopf 分岔,因此有鞍點、穩定焦點、不穩定焦點存在,如圖3(b) 所示.H 與LP 之間的藍色虛線表示不穩定焦點,當施加小擾動時,密度振蕩且振幅變得越來越大,最終形成擁堵.H 與HC 之間的洋紅色虛線為極限環的最大值和最小值,當施加小擾動時,密度振蕩且振幅趨于極限環,最終形成等幅振蕩,即走走停停現象.從區域Ⅲ和Ⅳ的單參數分岔結構可以看出,穩定交通流出現在焦點處 (實線).圖3(b) 的Hopf 點Lyapunov 第一指數 3.969 532×10-3為正為亞臨界Hopf 分岔,該處產生不穩定極限環.接下來,分析不同的分岔點對交通狀態的影響.

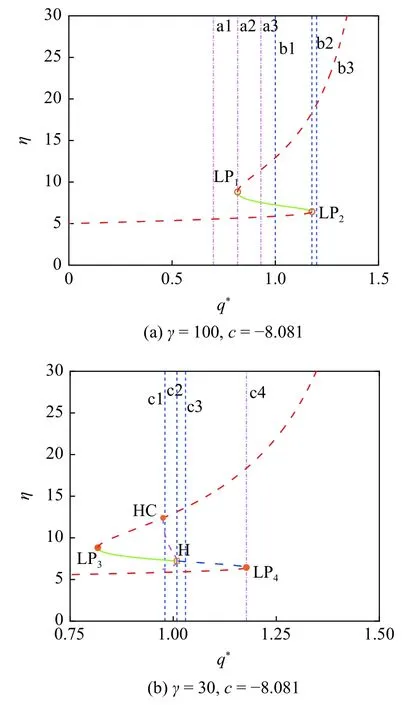
圖3 關于 q* 的單參數分岔結構Fig.3 The one-parameter bifurcation structure ofq*

3.2 關于 q* 的相平面分析

當 γ=100 時,交通流經歷了自由流狀態 (FT)-震蕩-擁堵 (J) 的過程,如圖3(a) 單參數分岔結構所示.當 (q*,η)=(1.177,6.432) 時,則=-14.348 3,-(1-ρmη)2=-0.082 024 96,因此 R=7.160 3×104,=1.176 918 133 57滿足q*=且R ≠0 條件,所以系統發生鞍結分岔 (LP),分析在 LP1附近交通流密度的變化,如圖4 所示.

在 q*=1 時,對應圖3(a) 的b1 曲線,系統存在鞍點 (5.883,0)、穩定焦點 (7.251,0) 和鞍點 (12.93,0),如圖4(a) 所示.從軌跡走向可以看出,從鞍點 (12.93,0) 出發的軌線吸引到焦點 (虛線);交通流為振蕩擁擠交通轉化為自由流 (FT).在 q*=1.177 時,對應圖3(a) 的b2 曲線,系統存在鞍結點 (6.432,0) 和鞍點 (18.34,0),如圖4(c) 所示.從軌跡形式可以看出,由于鞍結分岔,穩定焦點與鞍點相遇,部分曲線穩定,其余曲線不穩;交通流為自由流 (FT) 和振蕩流共存.在 q*=1.2 時,對應圖3(a) 的b1 曲線,系統存在鞍點(19.36,0),交通流為自有流.隨著 q*的增大,交通流發生了穩定到不穩定的轉變.當(q*,η)=(0.817 3,5.657)時,為系統的LP 分岔點,分析在 LP2附近交通流密度的變化,如圖5 所示.

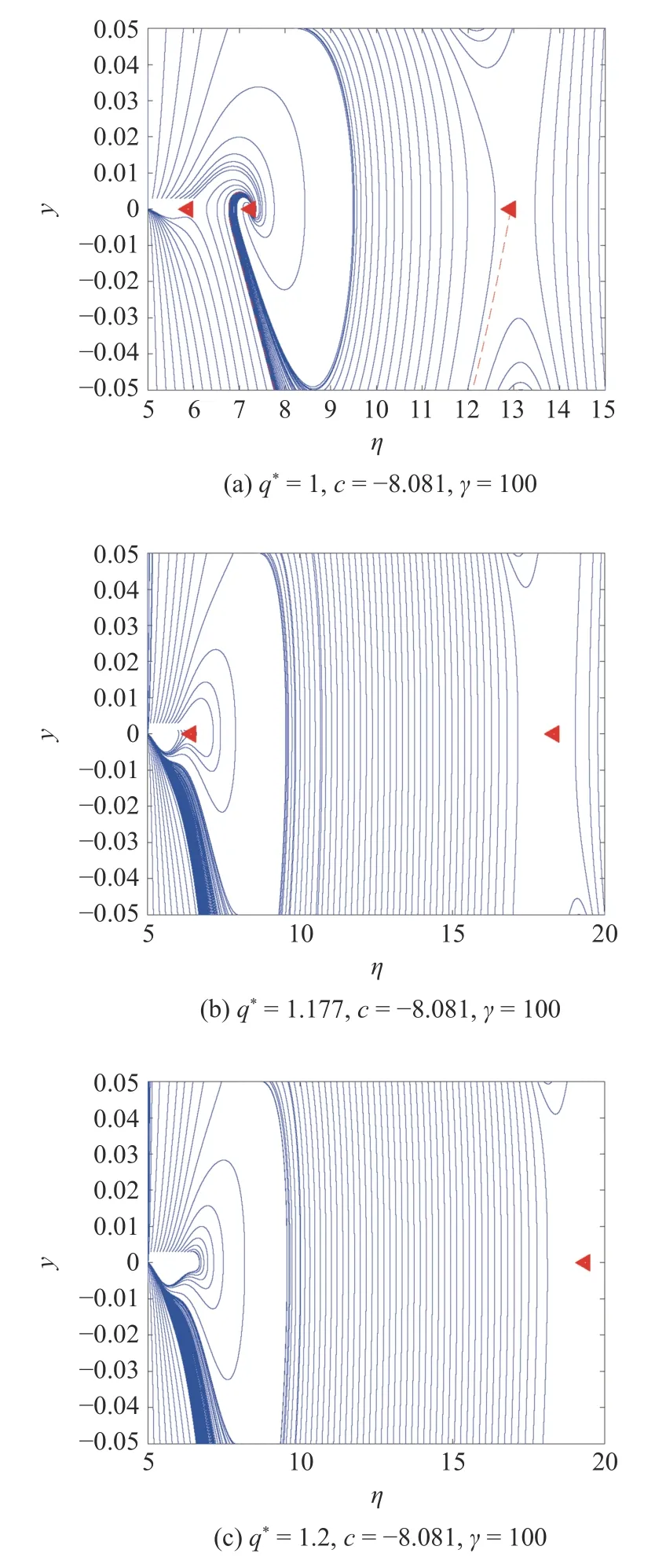
圖4 鞍結分岔 LP1 附近的相平面Fig.4 Phase plan near saddle-node bifurcation LP1

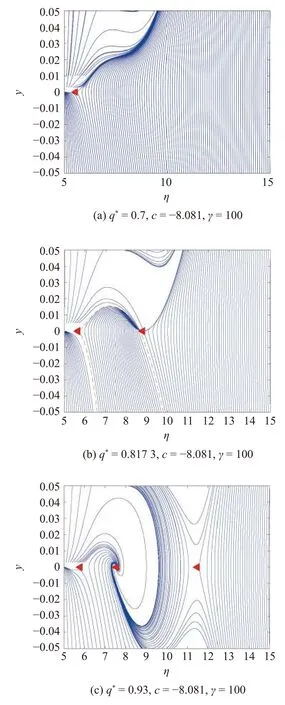
圖5 鞍結分岔 LP2 附近的相平面Fig.5 Phase plan near saddle-node bifurcation LP2

在 q*=0.7 時,對應圖3(a) 的a1 曲線,系統存在鞍點 (5.54,0),如圖5(a) 所示.交通流為自由流.在q*=0.817 3時,對應圖3(a) 的a2 曲線,系統存在鞍結點 (8.804,0) 和鞍點 (5.657,0),如圖5(b) 所示.從軌跡形式可以看出,由于鞍結分岔,穩定焦點與鞍點相遇,從另一個鞍點出發的曲線吸引到鞍結點,在虛線內曲線穩定,其余曲線為不穩;交通流為振蕩流和自由流 (FT) 共存.在 q*=0.93 時,對應圖3(a) 的a3 曲線,系統存在鞍點 (5.787,0)、穩定焦點 (7.536,0) 和鞍點 (11.48,0),如圖5(c) 所示.從軌跡形式可以看出,由于焦點的吸引部分曲線趨于焦點,兩邊的鞍點的作用使部分曲線不穩定;交通流為振蕩擁擠交通轉化為自由流 (FT).隨著 q*的增大,交通流出現不穩定到穩定的變化.根據圖4 和圖5 分析知,當0.873(LP)＜q*＜1.177(LP)時,系統有穩定交通流存在.當 γ=30 時,交通流經歷了自由流狀態 (FT)-時走時停態 (TSG)-振蕩態-擁擠態 (J) 的過程,單參數分岔結構如圖3(b) 所示.當 q*=0.817 3 時,為系統的LP 分岔點,分析在 LP3附近交通流密度的變化,如圖6 所示.

在 q*=0.6 時,系統存在鞍點 (5.45,0),如圖6(a)所示.交通流為自由流 (FT).在 q*=0.817 3 時,系統存在鞍結點 (8.804,0) 和鞍點 (5.657,0),如圖6(b) 所示.從軌跡形式可以看出,由于鞍結分岔,穩定焦點與鞍點相遇,在虛線內曲線為穩定,其余曲線為不穩定;交通流為自由流 (FT) 和振蕩態共存.在q*=0.93時,系統存在鞍點 (5.787,0)、穩定焦點 (7.536,0) 和鞍點 (11.478,0),如圖6(c) 所示.從軌跡形式可以看出,從鞍點 (10.9,0) 吸引到焦點,有穩定曲線產生;交通流為振蕩交通轉化為自由流 (FT).隨著 q*增大,交通流出現不穩定到穩定的變化.當(q*,η)=(1.009,7.218)時,為系統的Hopf 點.分析在Hopf 分岔附近交通流密度的變化,如圖7 所示.

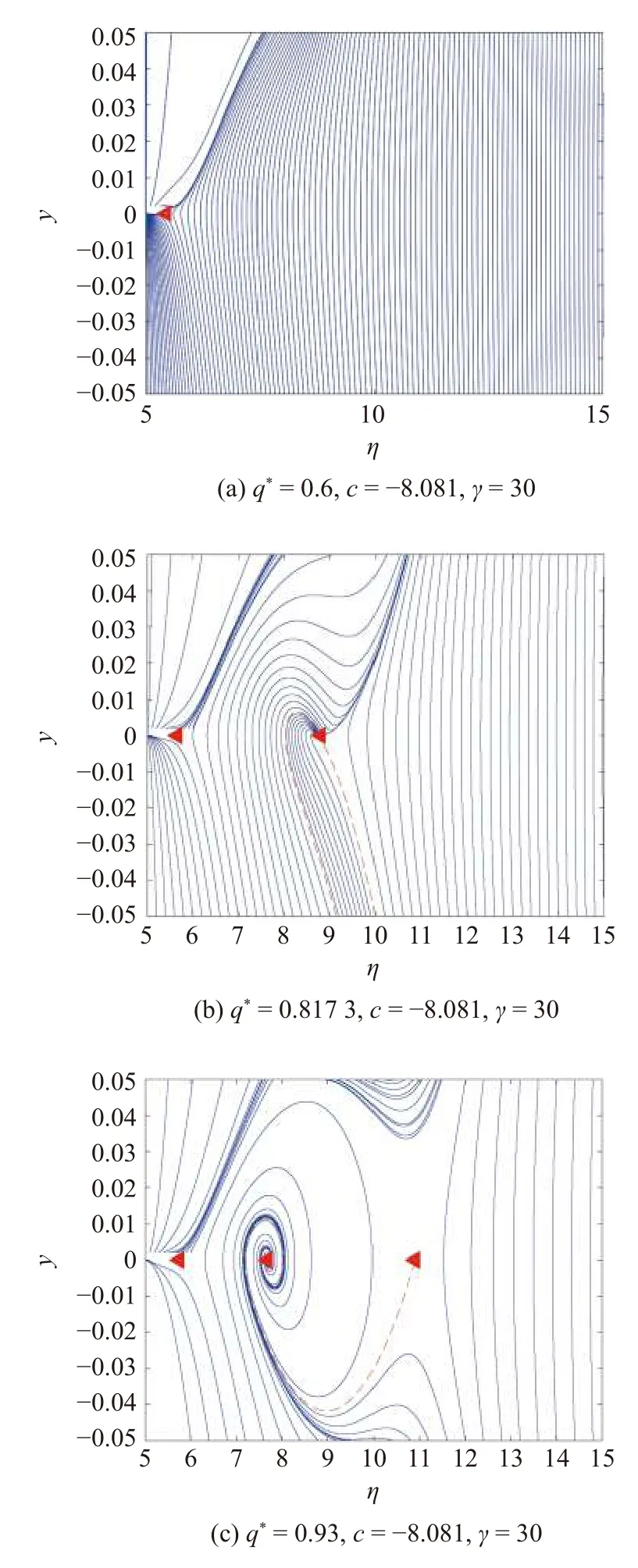
圖6 鞍結分岔 LP3 附近的相平面Fig.6 Phase plan near saddle-node bifurcation LP3

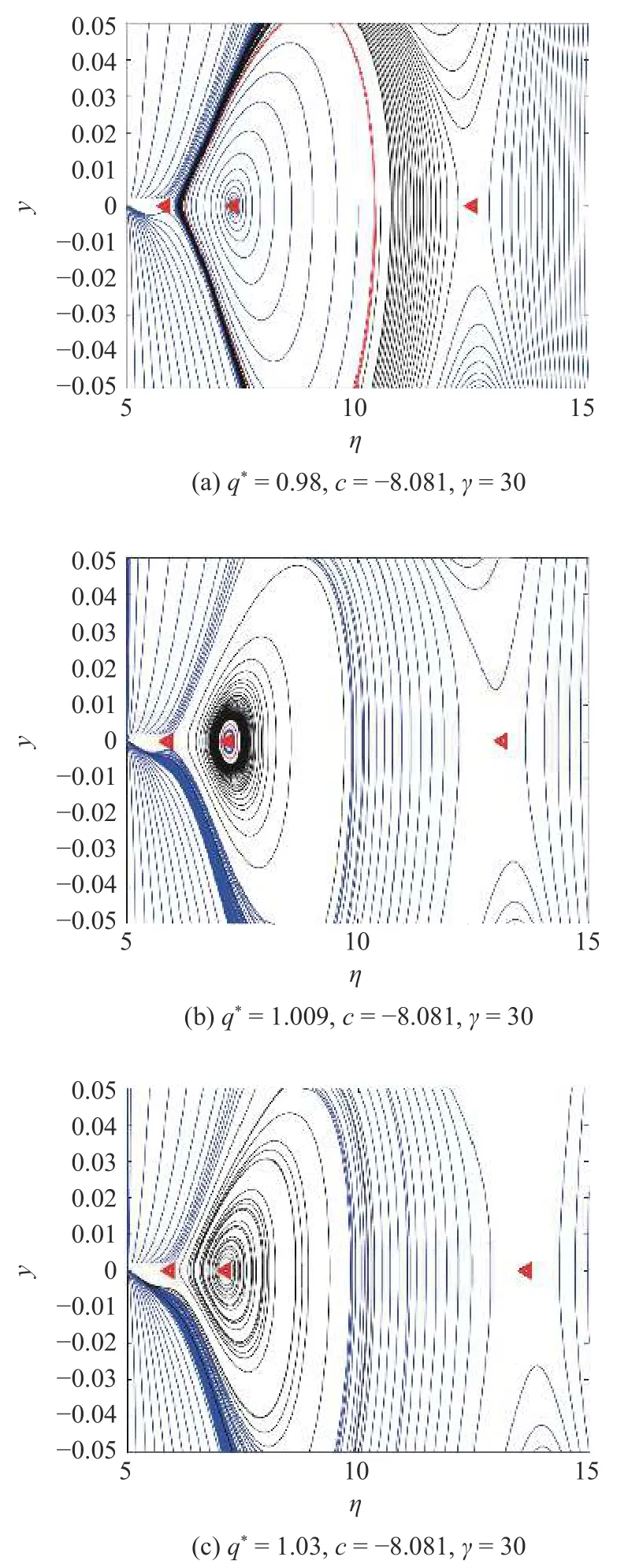
圖7 Hopf 分岔附近的相平面Fig.7 Phase plane near Hopf bifurcation

在 q*=0.98 時,對應圖3(b) 的c1 曲線,系統存在鞍點 (5.854,0)、穩定焦點 (7.326,0) 和鞍點 (12.5,0),如圖7(a) 所示.根據軌跡形式,它包含一個不穩定的極限環,環內和環外曲線在 z →-∞ 時趨于極限環,形成等幅振蕩;交通流有走走停停態 (TSG) 態,在右側鞍點處有自由流 (FT) 形式.在 q*=1.009 時,對應圖3(b) 的c2 曲線,系統存在鞍點 (5.897,0)、Hopf 點 (7.218,0) 和鞍點 (13.14,0),如圖7(b) 所示.從軌跡形式可以看出,紅色環內為穩定狀態,環外時不穩定振蕩;交通流為振蕩擁擠交通變為擁堵態 (J),但有一小部分振蕩是走走停停的現象.在q*=1.03時,對應圖3(b) 的c3 曲線,系統存在一個鞍點 (5.93,0),不穩定的焦點 (7.143,0) 和鞍點 (13.64,0),如圖7(c) 所示.從軌跡形式可以看出,由不穩定焦點處振蕩至不穩定;交通流為振蕩擁擠交通變為擁堵態(J).隨著 q*的增加,振蕩擁擠流變成振蕩流的一部分,然后演化為走走停停的現象.當(q*,η)=(1.177,6.432)時,為系統的LP 分岔點,分析在 LP4附近交通流密度的變化,如圖8 所示.

在 q*=1.1 時,系統存在鞍點 (6.063,0)、不穩定焦點 (6.897,0) 和鞍點 (15.56,0),如圖8(a) 所示.從軌跡形式可以看出,從焦點附近出發的軌線趨于最小密度;交通流為自由流態 (FT).在 q*=1.177 時,對應圖3(b) 的c4 曲線,系統存在鞍結點 (6.432,0) 和鞍點 (18.34,0),如圖8(b) 所示.從軌跡形式可以看出,由于鞍結分岔,穩定焦點與鞍點相遇,鞍結點附近曲線穩定,其余曲線不穩定;交通流為振蕩態與自由流 (FT) 共存.在 q*=1.3 時,系統存在鞍點 (25.52,0),如圖8(c) 所示.交通流為自由流 (FT).隨著 q*的增加,交通流出現自由流 (FT) 到擁擠態 (J) 的變化.由圖6～圖8 知,在 q*＜0.817 3(LP4) 產生自由流(FT),0.817 3(LP4)＜q*＜0.97(HC)為振蕩自由流(F T),0.97(HC)＜q*＜1.009(H)出現走走停停現象(TSG),1.009(H)＜q*為均勻擁擠態 (J).

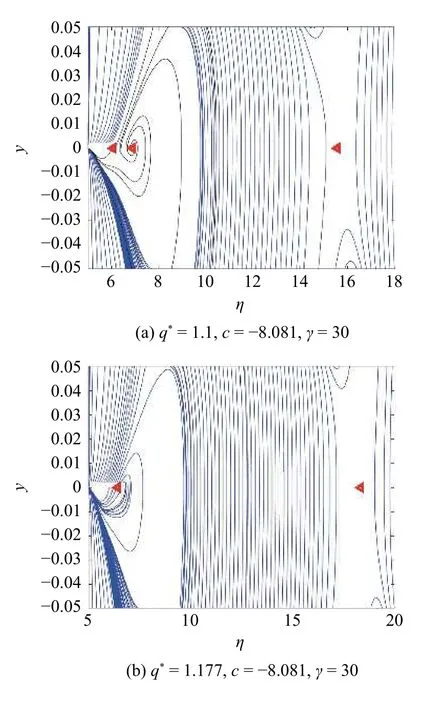
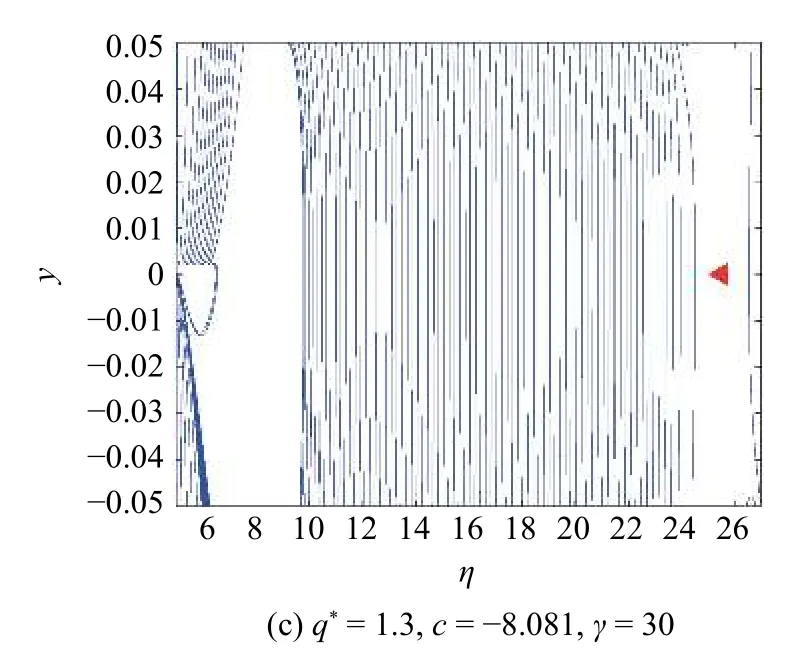
圖8 鞍結分岔 LP4 附近的相平面Fig.8 Phase plan near saddle-node bifurcation LP4

3.3 關于 γ 單參數分岔結構

隨著 q*值增大,γ 的分岔結構也發生了變化.根據不同分岔結構,圖1(a) 分成兩個分岔區域,分別在不同區域取值,研究關于 q*的單參數分岔結構,如圖9 所示.

當 q*=0.892 時 (即在圖1(a) 的區域Ⅰ內) 有Hopf 曲線和HC 曲線,因此系統存在穩定焦點和不穩定焦點.Hopf點處Lyapunov第一指數-2.918 477×10-4為負,Hopf 分岔為超臨界,H 上下的實線表示穩定極限環.如圖9(a) 所示,H 右邊實線代表穩定的焦點,當施加小擾動時,密度振蕩且振幅變得越來越小,最終穩定在焦點;H 左邊虛線表示不穩定焦點,在 z →+∞ 時,當施加小擾動時,密度越來越大,最終趨于穩定極限環.當 q*=0.901 時,即在圖1(a) 的區域Ⅱ內,如圖9(b) 所示,Hopf 點Lyapunov 第一指數 3.557 092×10-5為正,Hopf 分岔為亞臨界,H 上下之間的虛線表示不穩定極限環,z →-∞時,環內和環外的軌線趨于極限環.當存在小擾動時,密度振蕩并趨于不穩定極限環,形成等幅振蕩,最終形成走停現象.由于 γ ＞0 時,交通流系統有意義.在 γ ＞0 時,q*=0.892 系統只有穩定焦點,Hopf 點為 (-2.984 256,7.734 391) (如圖9(a) 所示);q*=0.892時,系統有不穩定焦點、穩定焦點、不穩定極限環存在,Hopf 點為 (0.358 938,7.682 751) (如圖9 (b) 所示).分析在Hopf 分岔附近交通流密度的變化,如圖10 所示.

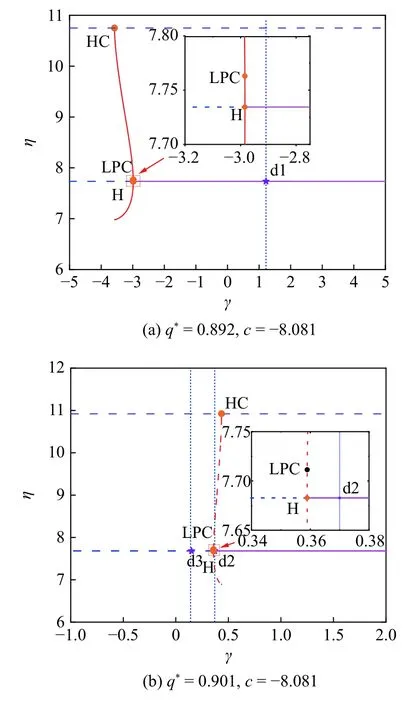
圖9 關于 γ 的單參數分岔結構Fig.9 The one-parameter bifurcation structure ofγ

當參數 q*=0.892 且γ ＞-2.984 (Hopf 分岔點)時,對應圖9(a) 的d1 曲線,系統存在穩定焦點(7.734,0),高密度鞍點 (10.749,0),如圖10(a) 所示.由于穩定焦點的吸引,軌線振蕩趨于焦點;交通流為振蕩交通轉化為自由流(FT),鞍點出形成擁堵(J).在 q*=0.901 和γ=0.14 ＜0.358 9 (Hopf 分岔點) 時,對應圖9(b) 的d2 曲線,系統存在不穩定焦點 (7.683,0),鞍點 (10.921,0),如圖10(b) 所示.由于不穩定焦點,軌線振蕩趨于不穩定;交通流為振蕩交通轉化為擁擠態 (J).在 q*=0.901 和q*=0.37 ＞0.358 9 (Hopf分岔點) 時,對應圖9(b) 的d3 曲線,系統存在穩定焦點 (7.683,0) 和不穩定極限環如圖10(c) 所示.從軌跡形式可以看出,它包含一個不穩定的極限環,環內和環外曲線在 z →-∞ 時趨于極限環,形成等幅振蕩;交通流為走走停停態 (TSG).

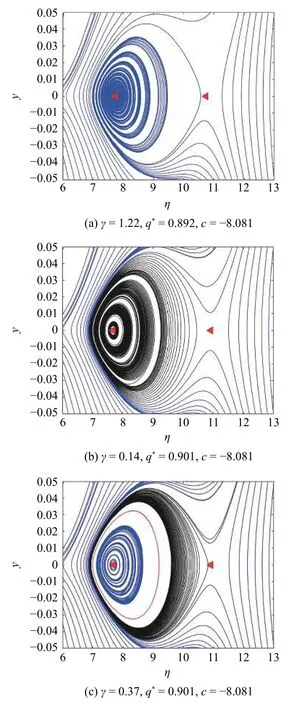
圖10 關于Hopf 分岔的相平面Fig.10 The phase plane of Hopf bifurcation

4 結論

本文提出了一個最優速度隨記憶變化的宏觀交通流模型.首先,原始模型狀態變量的最大值為0.2 veh/m,通過變量代換將問題轉化為系統穩定性問題;其次,通過余維2 分岔方法,改變了只能由行波參數發現走停現象的規律.然后,通過雙參數分岔,了解了參數之間的相互影響,并發現了系統存在Hopf 分岔、LP 分岔、BT 分岔和HC 分岔、CP 分岔、GH 分岔等各種分岔結構;再次,對雙參數分岔不同區域取值,得到不同單參數分岔結構,確定極限環、鞍結分岔和Hopf 分岔的值,給出相平面整體結構;最后,通過相位平面分析對模型的平衡點變化有了深刻的理解.數值模擬了相平面軌跡,通過對極限環、焦點和鞍點的動力學分析,解釋了不同動力學行為對擁堵交通中復雜現象的影響.通過不同分岔結構的相平面軌跡,分析對應的交通現象,提高高速公路觀測到的啟停波和局部簇的理解.

數值結果表明,駕駛員記憶的時間長度對交通流的穩定性有重要影響.總之,分析結果和數值模擬都表明,隨記憶變化的最優速度可以進一步提高交通流的穩定性.分岔分析方法可以描述和預測高速公路上的非線性交通現象,并有助于設計更好更合理的控制方案來改變交通擁堵現象.