高徑比對GaAs 熔體液橋熱毛細對流失穩的影響1)

周 游 曾 忠, 劉 浩 張良奇

* (重慶大學航空航天學院,重慶 400044)

? (重慶交通大學西南水運工程科學研究所,重慶 400016)

引言

熱毛細對流是沿流體-流體界面非均勻溫度導致的表面張力梯度驅動的對流,其廣泛存在于晶體生長[1-2]、液滴遷移[3-4]、3D 打印[5-6]等工業應用中,其中晶體生長是其重要的研究背景之一.浮區法是一種無坩堝高品質單晶生長技術,隨著航空航天技術的發展,空間微重力環境為浮區法生長更大尺寸和更高品質的單晶提供了可能.在空間微重力環境中,熱浮力對流極度衰減,熱毛細對流成為浮區法晶體生長中熔體物質與熱輸運的主要方式.由兩塊不同溫度同軸圓盤以及圓盤之間的液柱組成液橋模型,其可當成源于浮區法晶體生長技術的半浮區簡化模型.近40 年來,液橋模型已被廣泛運用于熱毛細對流研究.

熔體普朗特數對液橋熱毛細對流失穩機制和失穩模式有重要影響.Smith 和Davis[7]基于線性穩定性分析研究了不同普朗特數無限大平面液層中熱毛細對流的不穩定性,發現了2 種對流失穩類型.Levenstam等[8-9]通過三維數值模擬和實驗對低普朗特數熔體液橋熱毛細對流研究時發現,熱毛細對流第一次失穩是從二維軸對稱定常流動轉變為三維定常對流.Chen 等[10]采用微擾動法研究了低普朗特數液橋熱毛細對流失穩,研究表明:當Pr≤0.1 時,液橋熱毛細對流的第一次失穩為靜態失穩.Ichiro 等[11]通過實驗對高普朗特數熔體液橋熱毛細對流進行了研究,研究表明隨著溫差的增大,熱毛細對流第一次失穩是從二維軸對稱定常流動轉變為三維振蕩對流.Wanschura 等[12]通過線性穩定性分析研究了不同普朗特數對液橋熱毛細對流的影響,結果表明熱毛細對流失穩存在兩種失穩類型:當Pr≤0.05 時,液橋熱毛細流動失穩從二維軸對稱定常對流轉變為三維定常對流,當0.5≤Pr≤4.8 時,液橋熱毛細對流失穩從二維軸對稱定常對流轉變為三維振蕩對流,兩種失穩模式具有不同失穩機制.Chen 等[13]采用與Wanschura 等[12]同樣的液橋模型,通過線性穩定性分析研究了10-10≤Pr≤8.0 的熱毛細對流失穩,結果表明:當Pr≤0.06 時,熱毛細對流失穩是由水動力學慣性機制引起,并且其失穩模式為靜態失穩;當Pr≥0.1 時,失穩是由熱毛細機制引起,并且其失穩模式為振蕩失穩.2001 年,Levenstam 等[14]結合數值模擬和線性穩定性分析研究了0.001≤Pr≤7 范圍內液橋熱毛細流的失穩機制,他們的研究表明:當0.001≤Pr≤0.05 時,熱毛細對流失穩是由水動力學慣性機制引起,其失穩模式為靜態失穩,當0.057≤Pr≤0.068,熱毛細對流失穩主要是由水動力學慣性機制引起,但其失穩模式轉變為振蕩失穩.當0.07≤Pr≤1.80 時,熱毛細對流失穩是由水動力學慣性機制和熱毛細機制共同作用引起,其失穩模式為振蕩失穩,當0.183≤Pr≤7 時,熱毛細對流失穩是主要是由熱毛細機制引起,其失穩模式為振蕩失穩.上述文獻結果表明:液體普朗特數對液橋熱毛細對流的失穩機制和失穩模式具有重要影響.對高普朗特數液體,熱毛細對流第一次失穩是從二維軸對稱定常對流轉變為三維周期性振蕩對流,其失穩機制是熱毛細失穩機制;對低普朗特數液體,熱毛細對流第一次失穩是從二維軸對稱定常對流轉變為三維定常對流,失穩機制為水動力學慣性失穩機制.

針對錫熔體(Pr=0.009)的熱毛細對流,Li 等[15]數值模擬研究了液橋高徑比對熱毛細對流失穩的影響,結果顯示:當高徑比在0.6～2.2 之間時,熱毛細對流失穩臨界Marangoni 數(Mac)隨著高徑比的減小而單調增加,其熱毛細對流失穩模式均為靜態失穩.Rybicki 和Floryan[16]數值模擬研究了液橋的熱毛細對流,結果表明高徑比對液橋熱毛細流動有重要影響.Velten 等[17]通過地面實驗研究了高徑比對液橋熱毛細對流的影響,結果表明隨著高徑比的增加Mac逐漸減小.Chen 和Hu[18]通過線性穩定性分析研究了液橋的高徑比對半浮區液橋熱毛細對流的影響,隨著高徑比的增加Mac數和臨界頻率隨之減小.Nishino 等[19]結合空間實驗和線性穩定性分析方法,研究了高徑比對高普朗特數液橋熱毛細對流不穩定性的影響,其研究結果表明:當Pr=67 時,在高徑比As=1.25 左右,臨界頻率和Mac出現突降現象,其失穩模式為振蕩失穩.吳勇強等[20]通過地面實驗研究了液橋高徑比對液橋起振溫差的影響,研究表明隨著高徑比的增大液橋內的起振溫差逐漸呈減小趨勢.王佳等[21]對大尺寸液橋的浮力-熱毛細對流進行了地面實驗,實驗發現在高普朗特數情況下,在Mac附近,流場內會有行波現象出現,隨著高徑比的變化,其流動模式發生改變.Kang 等[22]在天宮二號上進行了高普朗特數液體橋熱毛細對流的實驗研究,以液橋高徑比和體積比為特征,研究了幾何參數對液橋熱毛細對流失穩臨界條件的影響,首次完整地得到了微重力條件下高徑比-體積比參數空間內熱毛細對流不穩定性的臨界條件和振蕩特性.Wang等[23]基于地面實驗,研究了存在重力場作用時,幾何參數(高徑比和體積比)對大普朗特數大尺寸液橋熱毛細對流失穩臨界條件的影響,在不同的幾何參數下出現了6 種不同的失穩狀態.Liu 等[24]通過線性穩定性分析研究了高徑比對環形液池熱毛細對流(Pr=0.011 和Pr=1.4)的影響,研究發現:當高徑比較小時,失穩模式為振蕩失穩;當高徑比較大時,失穩模式為靜態失穩,這表示高徑比對環形液池熱毛細對流的失穩模式轉變有影響,但是該現象尚未在液橋熱毛細對流研究的文獻中報道.

目前,雖然文獻已有很多高徑比對液橋熱毛細流失穩影響的研究,但研究主要聚焦于高普朗特數熔體和低普朗特數熔體的熱毛細對流失穩,而較少關注普朗特數在0.057≤Pr≤0.8[14]范圍液橋的熱毛細流失穩,特別缺乏這一范圍內高徑比對其熱毛細失穩影響的研究.本文針對GaAs 熔體(Pr=0.068),采用譜元法對基態解進行求解,然后基于線性穩定性分析確定失穩臨界參數Mac,最后結合能量分析方法研究對流失穩的物理機制,研究高徑比對液橋熱毛細對流失穩臨界參數、失穩模式和失穩機制的影響.

1 數學模型和數值方法

1.1 物理模型與基本控制方程

采用圖1 所示的液橋模型,液橋由中心軸線重合的圓盤和圓形液柱組成,圓柱形液橋高度為H,半徑為R,高徑比定義為As=H/R.液橋上端為低溫固壁(φc),下端為高溫固壁(φh),熔體當成不可壓縮牛頓流體.假設表面張力為溫度的線性函數,圓柱自由表面絕熱并且忽略自由表面變形.

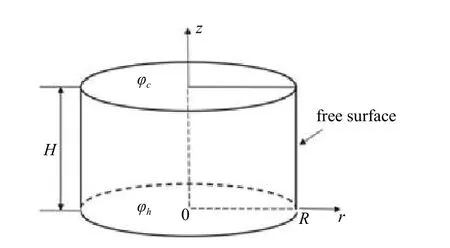
圖1 半浮區液橋模型Fig.1 Floating half-zone model

分別用H,υ/H,H2/υ 和 ρυ2/H2作為長度、速度、時間和壓力的特征物理量,對流體的控制方程進行無量綱化,其中 υ 是運動學黏性系數,ρ 是密度,無量綱溫度定義為 T=(φ-φc)/(φh-φc),其中φc為液橋低溫圓盤固壁溫度,φh為高溫圓盤固壁高溫,φ表示表示液橋內任意一點溫度.熱毛細對流失穩前是二維軸對稱定常流,失穩后變為三維對流.采用柱坐標(r,θ,z),r 為徑向坐標,θ 為周向坐標,z 為軸向坐標.無量綱控制方程為

無量綱邊界條件可以表示為:

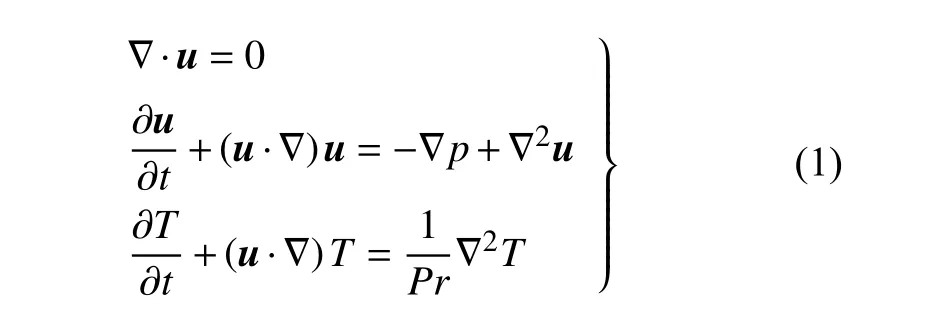
(1) 自由表面(r=1/As)

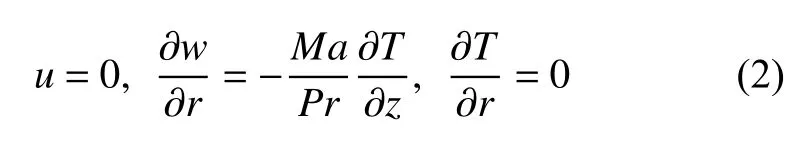
(2) 熱壁(z=0)

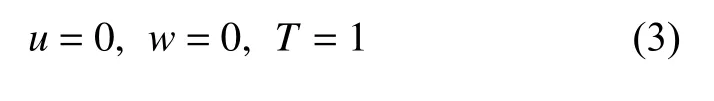
(3) 冷壁(z=1)

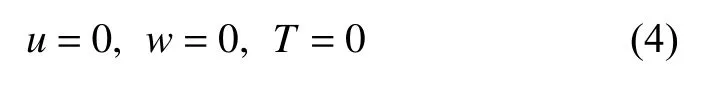
其中u 表示徑向速度,w 表示軸向速度,無量綱參數Pr 以及Ma 分別定義為

其中 κ 為熱擴散系數,γT為流體表面張力系數,Δφ=φh-φc.

1.2 線性穩定性分析

為了得到高精度的失穩臨界條件,采用基于時間分裂法的譜元法求解方程式(1)～式(4),得到定常軸對稱的基態解,然后在所得二維基態解上施加一個三維小擾動[25]

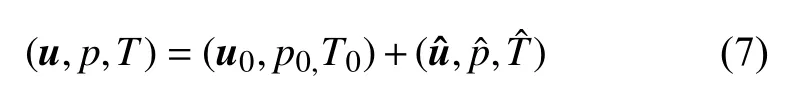
其中 u0,p0和 T0表示速度、壓力和溫度的基態解,表示擾動速度、擾動壓力和擾動溫度.將式(7)代入到方程式(1)～式(4)中,并忽略高階擾動項可導出擾動控制方程

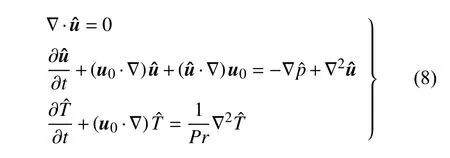
擾動邊界條件為:

(1) 自由表面(r=1/As)

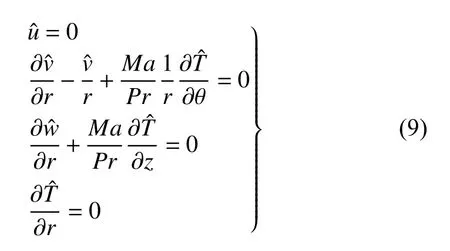
(2) 熱壁(z=0)

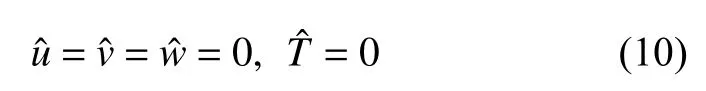
(3) 冷壁(z=1)

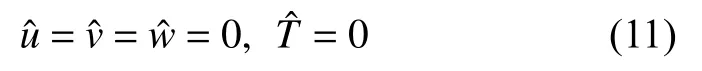
將擾動量表示為正則模形式

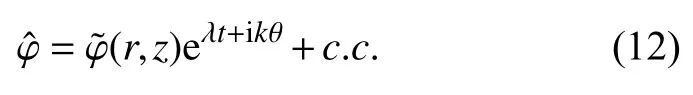
其中φ 表示u,v,w,T 和p,c.c.為復數虛部項的共軛.復數λ 可分為實部λr和虛部λi,其中實部λr表示為線性增長率,虛部λi表示為振蕩頻率?,k 表示為失穩波數.其中λr＜0 表示流動穩定,λr＞0 表示流動不穩定,而λr=0 則代表流動失穩的臨界狀態,線性穩定性分析正是要捕捉λr=0 時的臨界參數,在臨界條件下,λi=0 表示失穩是靜態失穩,λi≠0 表示失穩是振蕩失穩.在將表達式(12)代入式(8)～式(11),采用譜元法對擾動方程進行離散,得到一個廣義特征值問題,即

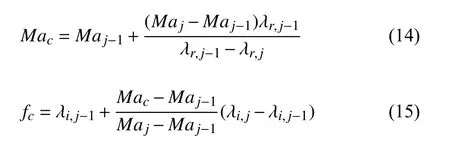
1.3 擾動能量分析

確定流動失穩臨界參數后,可通過擾動能量分析的方法來研究流動失穩機制.對擾動方程(8)中的動量方程乘以?并對求整個求解域進行積分,可得到擾動動能變化率表達式[12,30-31]

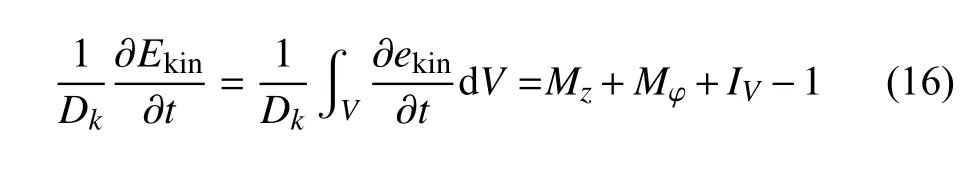
其中 ?ekin/?t 表示擾動動能的分布,Dk表示黏性耗散率,Mz和Mφ分別表示由擾動引起的熱毛細力沿液橋軸向和周向做功的功率,IV項表示從基態流場到擾動流場的動能傳遞率.則各個能量項的具體表達式為

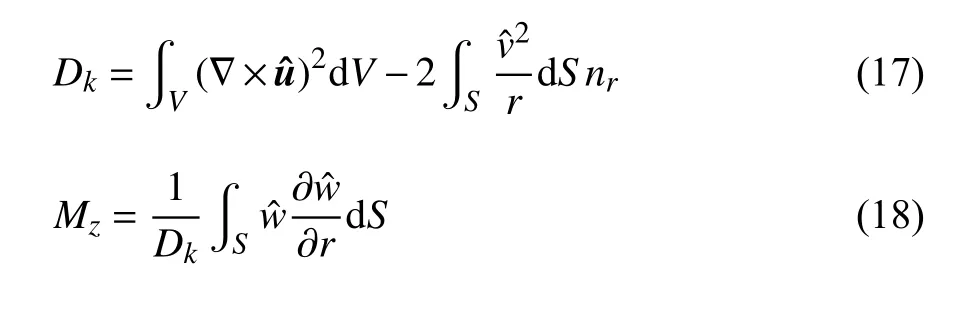
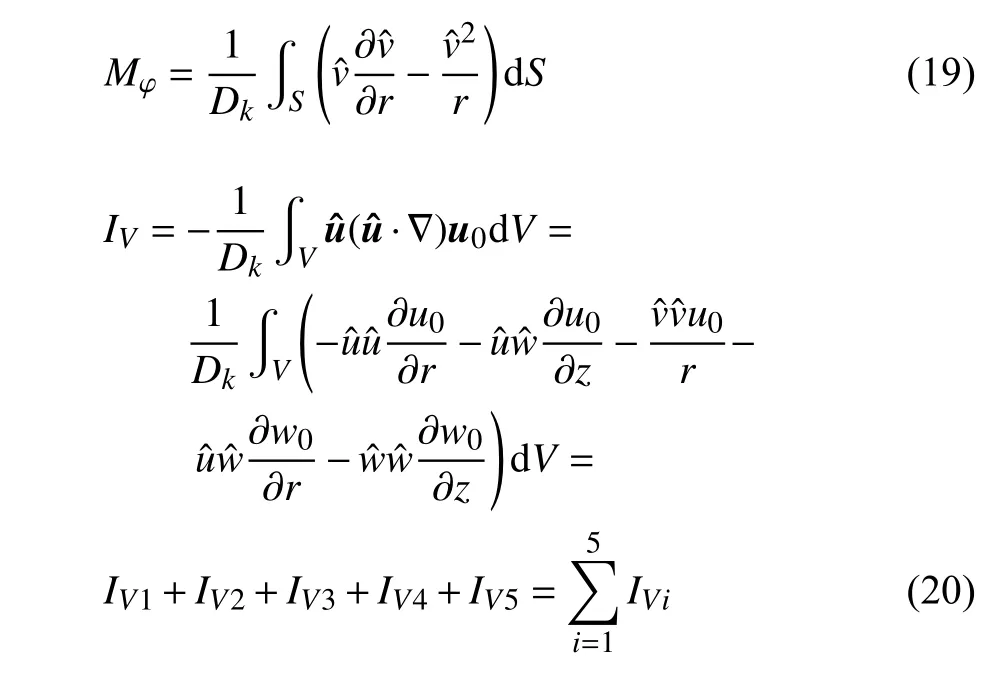
其中

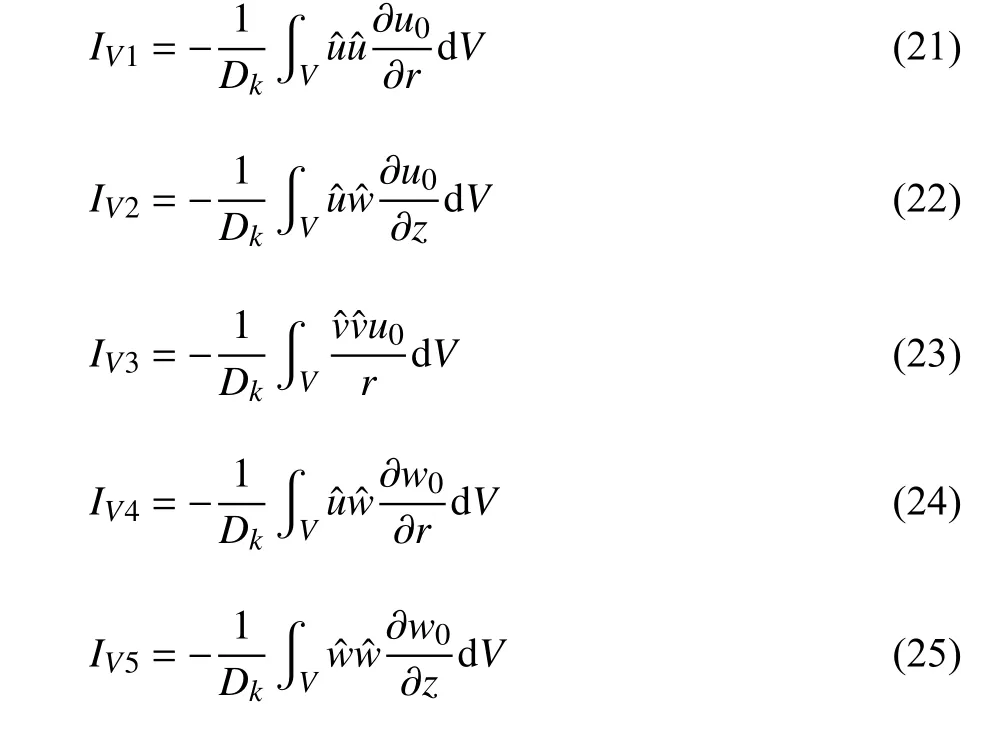
其中IV1,IV2和IV3表示基態徑向速度向擾動場的能量傳遞,而IV4和IV5則表示基態軸向速度向擾動場的能量傳遞.V 表示液橋的體積,S 表示自由表面.

2 結果與討論

2.1 網格依賴性和程序有效性驗證

選取Pr=0.068,液橋高徑比As=1,計算網格采用8r× 9z單元劃分,單元內分別采用5r× 5z,6r× 6z,7r× 7z階譜離散,對應網格節點為41 × 46,49 × 55,57 × 64.將不同網格的計算結果進行對比,如表1 所示,不同網格計算的波數吻合,Mac相對誤差較小.綜合考慮計算精度和計算效率,本文以下計算采用6r× 6z階譜離散.

表1 基于不同網格分辨率得到的熱毛細對流(Pr=0.068)失穩臨界Marangoni 數(Mac)和波數kcTable 1 The critical Marangoni number (Mac) and wave number kc for the instability of thermocapillary flow with Pr=0.068 under different mesh resolution conditions

選取液橋高徑比As=1 的熱毛細對流進行程序有效性驗證,計算網格采用8r× 9z單元劃分,6r×6z階譜離散,對應網格節點為49 × 55.將計算Mac轉化為Rec(Rec=Mac/Pr)與Levestam 等[14]的結果進行對比,如表2 所示.

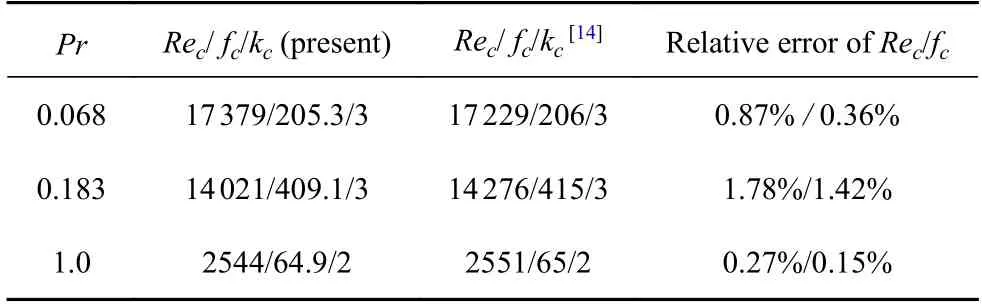
表2 計算失穩臨界參數(Rec,fc 和kc)與文獻[14]結果對比Table 2 The critical values (Rec,fc,kc) from the present computations against Ref.[14]

針對Pr=0.009 熔體熱毛細對流的失穩,基于我們自主開發譜元法程序計算結果與Li 等[15]的臨界參數(失穩臨界Marangoni 數(Mac)和波數kc)進行對比,如表3 所示.

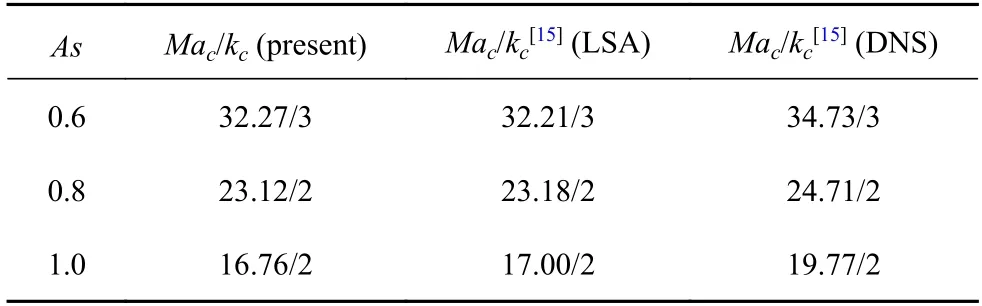
表3 計算失穩臨界參數(Mac 和kc)與文獻[15]結果對比Table 3 The critical values (Mac and kc) from the present computations against Ref.[15]

以上與Levestam 等[14]和Li 等[15]的結果對比表明:本文計算熱毛細對流失穩臨界參數與他們結果吻合,我們程序的有效性得到了驗證.

2.2 穩定性曲線與失穩模式

GaAs 熔體液橋熱毛細對流的基態是二維軸對稱定常對流.固定液橋的高度為1,液橋半徑的變化范圍為0.4≤R≤2.5,則對應液橋的高徑比變化范圍為2.5≥As≥0.4.離散采用6r× 6z階譜離散,計算網格采用(8r-14r) × 9z單元劃分,所以液橋軸向有54 個網格,徑向根據高徑比的不同有48～84 個網格.

如表4 所示,失穩波數隨著高徑比的增加而減小,失穩波數的變化符合Zeng 等[32]提出的高徑比和失穩波數之間的關系1.57≤kcAs≤3.14.如圖2 所示,臨界Mac數隨著高徑比增加,整體呈下降趨勢,Mac數在高徑比為0.67 和高徑比為1.18 處出現峰值點.表4 中的線性穩定性分析結果表明,在高徑比0.40≤As≤2.50 區間內,存在兩種失穩模式,當0.4≤As≤1.18 時,熱毛細對流從二維軸對稱定常對流轉捩為三維振蕩對流;當1.20≤As≤2.5 時,熱毛細對流從二維軸對稱定常對流轉捩為三維定常對流.

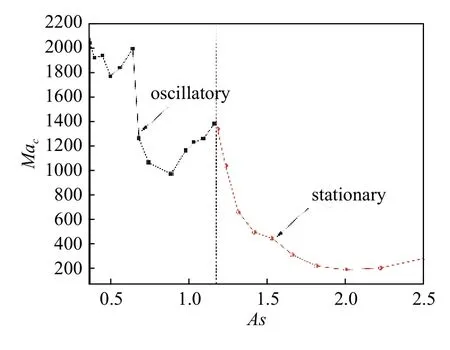
圖2 Mac 隨高徑比(As)的變化(Pr=0.068)Fig.2 The variation of Mac versus the aspect ratio As for Pr=0.068

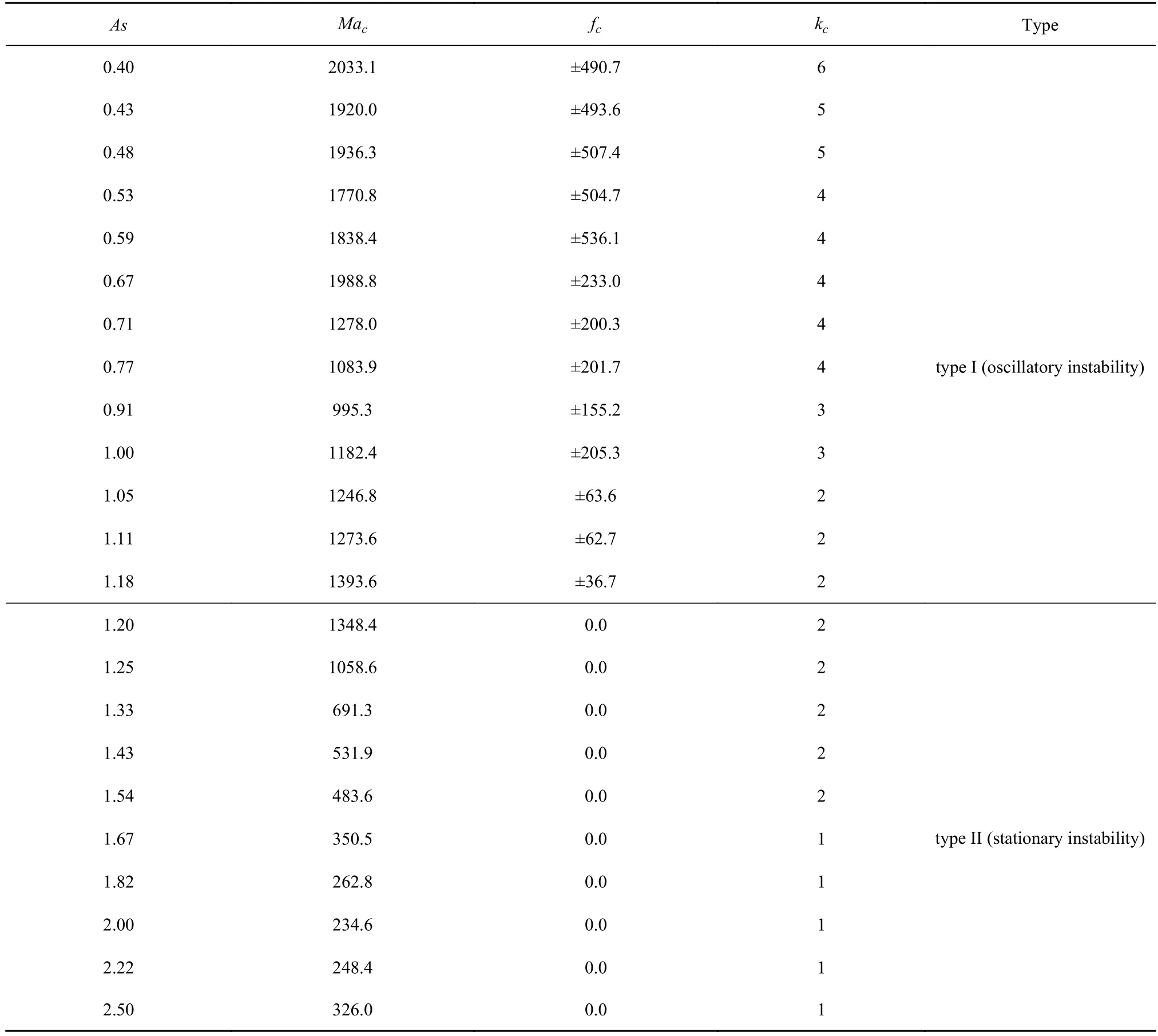
表4 Pr=0.068 時不同高徑比下的失穩臨界參數Table 4 The critical values at different aspect ratios for Pr=0.068

在圖3 中 IV項表示IV1項到IV5項的總和,M 項表示Mz和Mφ的總和.由圖3 可知,失穩主要是由水動力學慣性機制主導.結合表5 擾動能量平衡分析的結果可知,IV4和IV5是造成流動失穩的主要原因,且Mz和Mφ也占據一定比例,表明失穩是由水動力學慣性機制占主導,同時熱毛細機制對失穩有所貢獻.在高徑比As=1.82 處,由水動力學慣性機制主導的IV4+IV5的占比最大,而熱毛細機制引起的Mz+Mφ的占比最小,Levestam 等[14]針對高徑比As=1熔體液橋熱毛細對流失穩研究表明:當Pr=0.068時,液橋熱毛細對流是振蕩失穩,其失穩機制是水動力學的慣性失穩機制,這與本文的分析結果一致.下面具體介紹隨高徑比變化的兩種失穩模式.

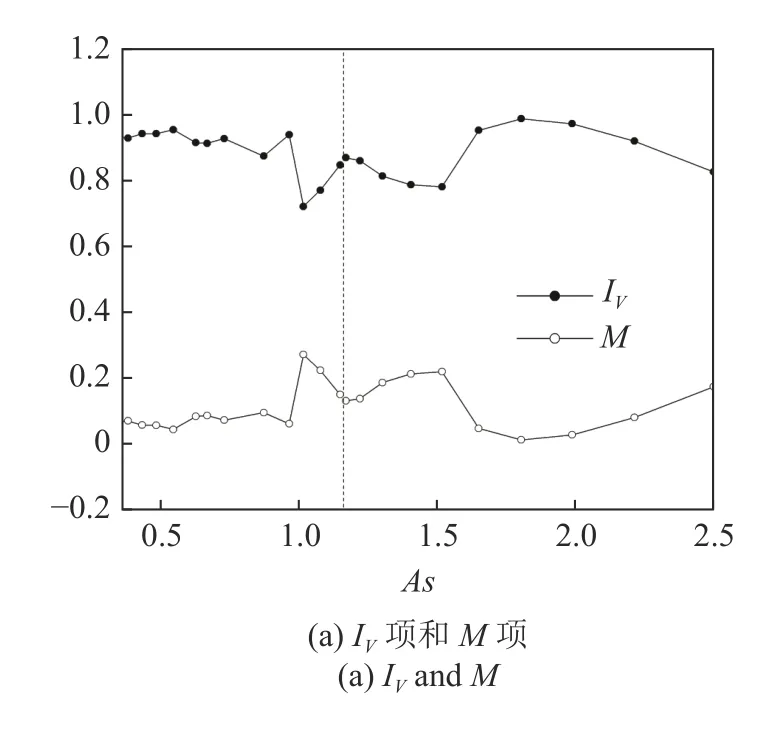
圖3 擾動能量隨高徑比As 變化Fig.3 The variation of the kinetic energy budgets with respect to the aspect ratio

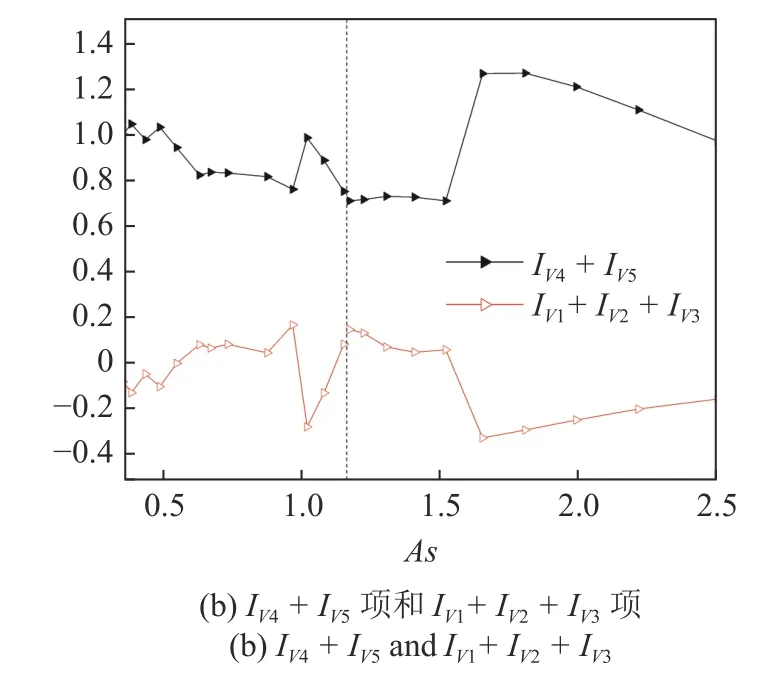
圖3 擾動能量隨高徑比As 變化(續)Fig.3 The variation of the kinetic energy budgets with respect to the aspect ratio (continued)

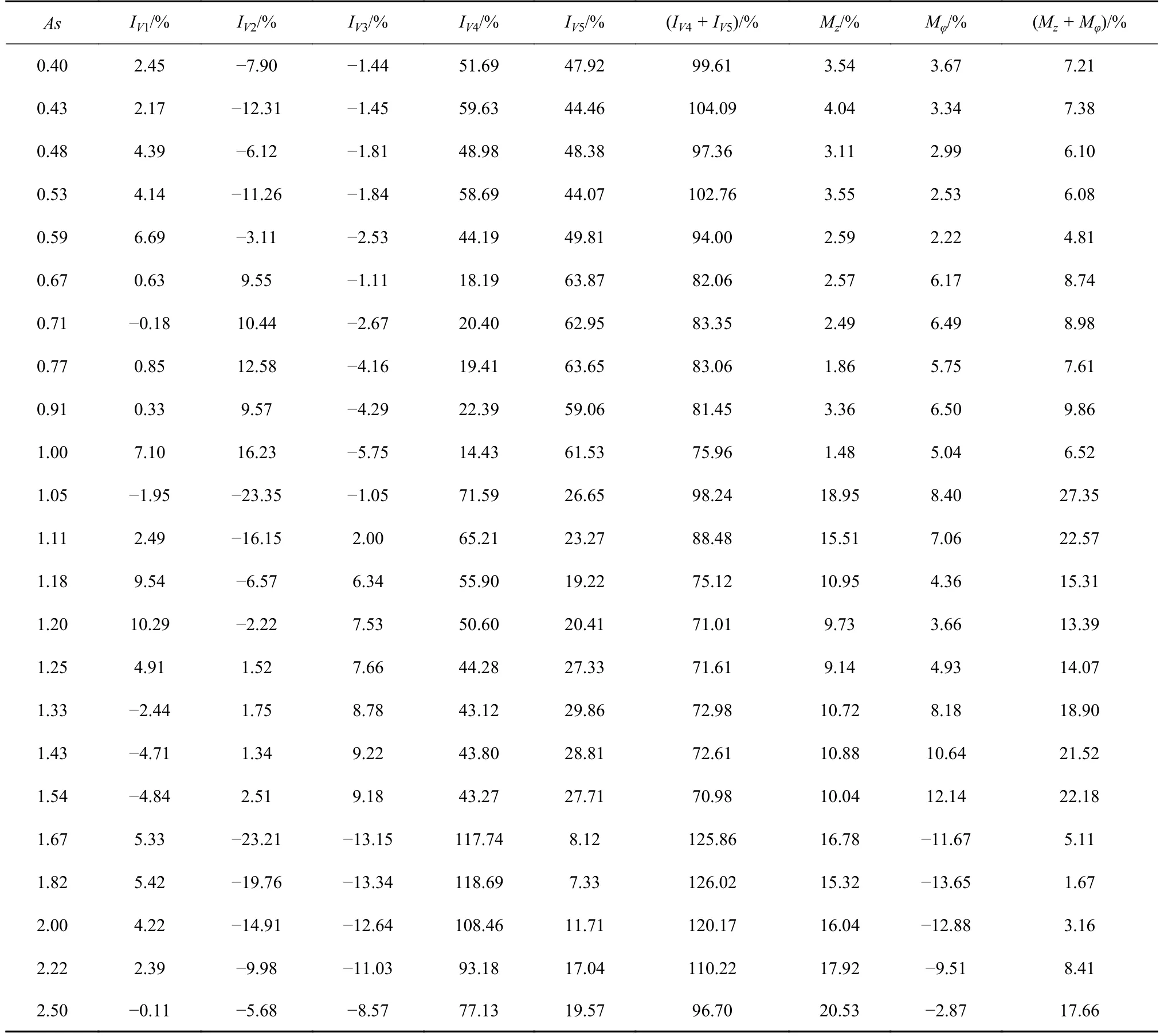
表5 Pr=0.068 時不同高徑比能量分析結果Table 5 The energy analysis results at different aspect ratios for Pr=0.068

2.3 失穩機制

2.3.1 失穩模式I (振蕩失穩)

由表4 可知,當0.40≤As≤1.18 時,失穩臨界頻率不等于零,即熱毛細對流從定常二維軸對稱流動失穩變為三維周期性振蕩對流.隨著高徑比的增加,失穩的臨界波數從kc=6 逐漸減少為kc=2.由表5和圖3 可知,在失穩模式I 中,失穩主要是由水動力學慣性機制作用,其中IV4和IV5是造成水動力學慣性失穩的主要原因;在這一失穩模式中,熱毛細機制對失穩也有一定貢獻.通過具體分析,失穩模式I 在不同高徑比范圍內,IV4項和IV5項對失穩的貢獻略微有所不同.當0.40≤As≤0.59 時,液橋流動失穩的能量主要是由IV4和IV5提供(約占100%),且二者比例相當;IV2和IV3為負值,代表其對對流具有穩定作用;同時擾動引起的熱毛細力做功(M 項)的貢獻占比小于8%(表5).當0.67≤As≤1.00 時,IV5項對液橋流動失穩的貢獻在60%左右,是造成流動失穩的主要原因;IV2已經為正值,IV3仍然為負值,熱毛細力做功的貢獻占比為6.52%～9.86%.當1.05≤As≤1.18 時,液橋流動失穩主要是由IV4項引起,其貢獻在65%左右,在這一高徑比區間Mz和Mφ的對失穩的貢獻有所增加,熱毛細力做功的貢獻占比為15.31%～27.35%,即熱毛細機制有所增強.下面將詳細分析上述3 個高徑比區間的失穩機制.

當0.40≤As≤0.59 時,由表5 可知,在這一高徑比區間中,Mz和Mφ對液橋的流動失穩貢獻較小,IV項(IV項表示IV1項到IV5項的總和)是造成流動失穩的主要原因.由圖4(a)擾動能量平衡圖可以直觀的看出,失穩主要由IV4和IV5造成,即基態的軸向速度徑向和軸向梯度為引起失穩的擾動動能傳遞了主要的能量.由局部擾動動能極值圖(圖4(b))可知,液橋熱毛細流動最危險的失穩區域出現在距液橋自由液面R/3 處并靠近熱壁附近.在液橋自由液面的擾動溫度圖(圖5(b))上分布了5 個熱極和5 個冷極,其中紅色表示熱極,藍色表示冷極,自由液面的擾動速度從熱極指向冷極,與擾動熱毛細力的方向相同.從圖5(a) 中可以看出,在靠近自由液面約R/3 處出現擾動溫度強斑,截面處的擾動速度從熱極指向冷極,并在冷極處形成擾動速度流胞.

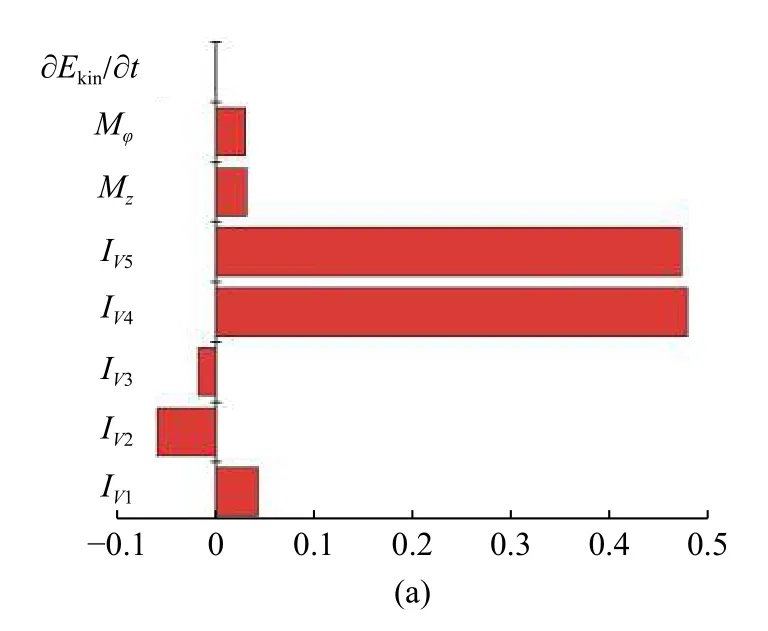
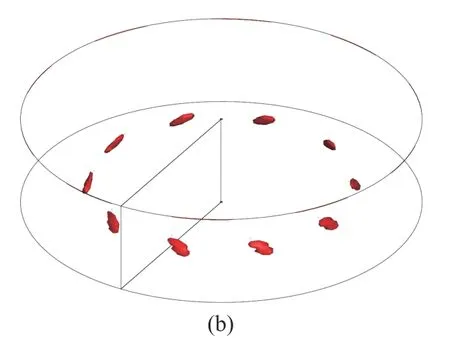
圖4 高徑比As=0.48,Pr=0.068 的臨界狀態(Mac=1936.3)下:(a)擾動能量平衡條狀圖,(b)局部擾動動能極值圖Fig.4 (a) The disturbance energy balance and (b) distribution of the local disturbance kinetic energy extreme value under critical condition(Mac=1936.3) at As=0.48,Pr=0.068

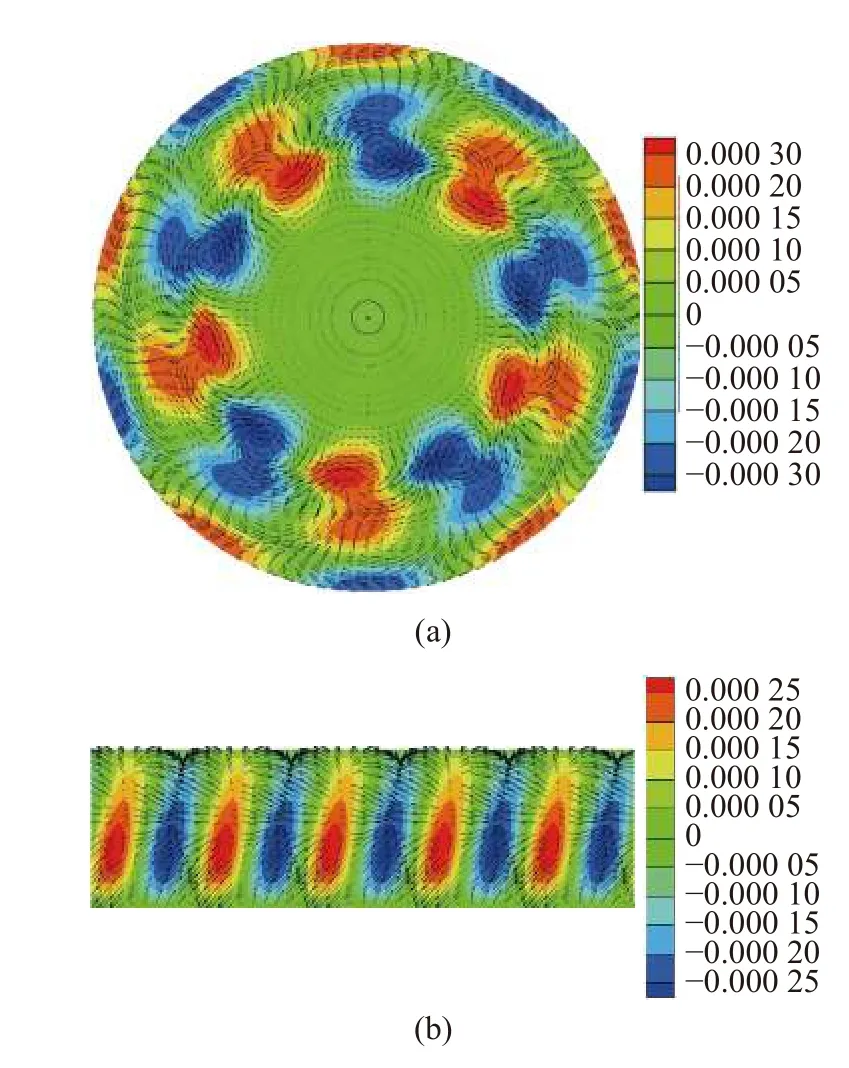
圖5 高徑比As=0.48,Pr=0.068 的臨界狀態 (Mac=1936.3) 下:(a) z=0.51 截面擾動溫度 (云圖) 和擾動速度矢量 (箭頭),(b)自由液面擾動溫度 (云圖) 和擾動速度矢量 (箭頭)Fig.5 The disturbance temperature (colored contour) and disturbance velocity vector (arrow):(a) the z=0.51 cross section,(b) the free surface under the critical condition (Mac=1936.3) at As=0.48,Pr=0.068

在0.67≤As≤1 區域內,由圖6 的擾動能量平衡圖可知,當高徑比在這一范圍內,失穩依然是由水動力學慣性機制占主導,但與0.40≤As≤0.59 這一高徑比范圍內失穩的具體擾動動能項存在一些差異,該高徑比范圍內液橋的流動失穩主要是由IV5項主導,即基態軸向速度的軸向梯度為流動失穩提供了主要能量.流動最危險的失穩位置出現在靠近熱壁處距離自由液面R/2 附近(圖6(b)).如圖7(a)中擾動溫度所示,該高徑比范圍內擾動溫度的特征與0.40≤As≤0.59 時不同,在這一高徑比范圍內,擾動溫度的特征是:在靠近對稱軸R/3 處和靠近自由液面附近出現強斑.在自由液面處擾動速度從熱極指向冷極,與擾動熱毛細力的方向相同(圖7(b)).

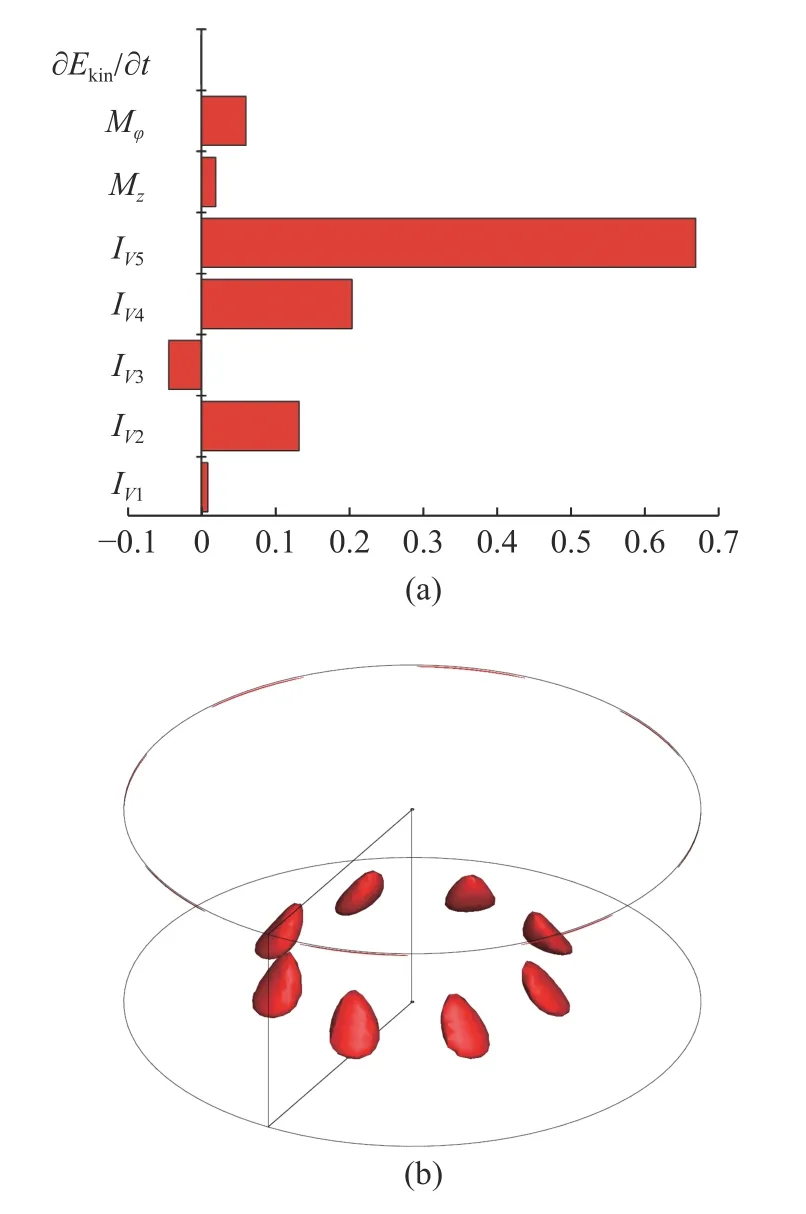
圖6 高徑比As=0.77,Pr=0.068 的臨界狀態 (Mac=1083.9) 下:(a)擾動能量平衡條狀圖,(b)局部擾動動能極值圖Fig.6 (a) The disturbance energy balance and (b) distribution of the local disturbance kinetic energy extreme value under critical condition(Mac=1083.9) at As=0.77,Pr=0.068

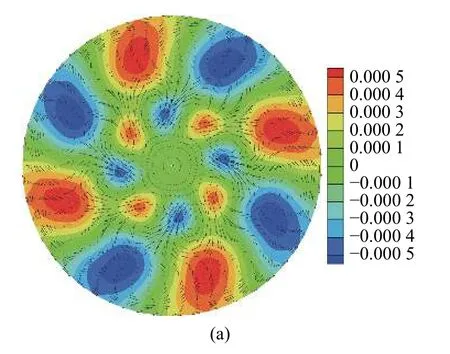
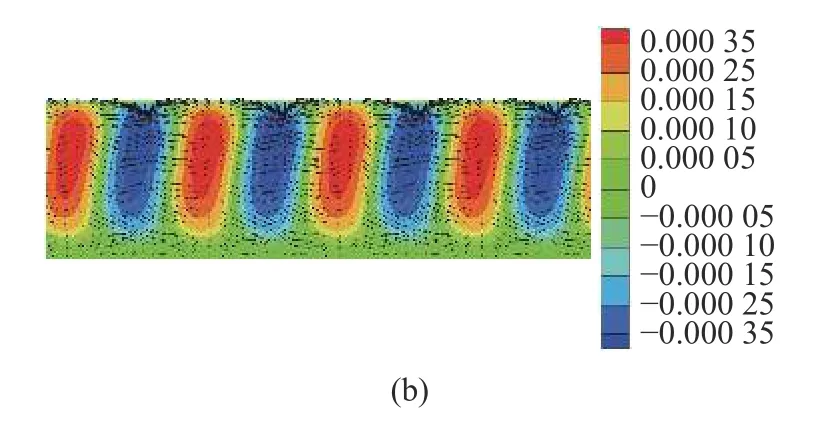
圖7 高徑比As=0.77,Pr=0.068 的臨界狀態 (Mac=1083.9) 下:(a) z=0.51 截面擾動溫度 (云圖) 和擾動速度矢量 (箭頭),(b)自由液面擾動溫度 (云圖) 和擾動速度矢量 (箭頭)Fig.7 The disturbance temperature (colored contour) and disturbance velocity vector (arrow):(a) the z=0.51 cross section,(b) the free surface under the critical condition (Mac=1083.9) at As=0.77,Pr=0.068

當1.05≤As≤1.18 時,由擾動能量平衡圖(圖8(a))可知,在這一高徑比范圍內,熱毛細機制對失穩的貢獻增大,但液橋熱毛細流動失穩仍是由水動力學的慣性機制主導.與上述兩種情況不同,在這一高徑比范圍內IV4項是造成失穩的主要原因,但 IV2項對流動失穩有較為明顯的抑制作用,即基態軸向速度的徑向梯度為流動失穩提供了主要能量,而基態徑向速度的軸向梯度有抑制流動失穩的作用.根據圖8(b)可知,最危險的失穩位置出現在熱壁附近,并距離對稱軸R/3 處.從自由液面展開圖(圖9(a))顯示:在靠近冷壁附近擾動速度從熱極指向冷極,而在靠近熱壁附近擾動速度從冷極指向熱極.根據z=0.20,z=0.51 和z=0.74 截面擾度溫度和擾動速度矢量圖(圖9(b)～圖9(d))可知,在z=0.20 截面處擾動速度從冷極指向熱極附近,擾動溫度模式的特征為輪輻狀強斑,并且布滿整個液橋橫截面;在z=0.51 截面處,擾動速度在靠近對稱軸附近是由熱熱極指向冷極,在靠近自由液面附近是由冷極指向熱極,從而擾動速度在熱極和冷極之間形成一個擾動流動循環,擾動溫度模式特征為:在靠近自由液面附近形成橢圓形強斑;在z=0.74 截面中擾動速度從熱極指向冷極,擾動溫度特征為:在自由液面附近和靠近自由液面R/3 處形成強斑.

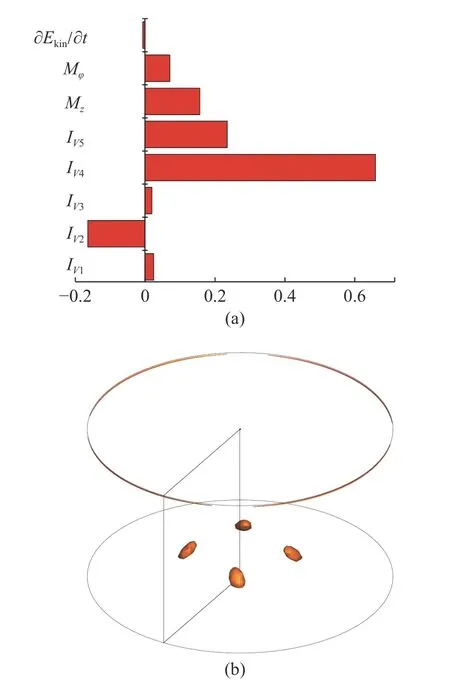
圖8 高徑比As=1.11,Pr=0.068 的臨界狀態 (Mac=1273.6) 下:(a)擾動能量平衡條狀圖,(b)局部擾動動能極值圖Fig.8 (a) The disturbance energy balance and (b) distribution of the local disturbance kinetic energy extreme value under critical condition(Mac=1273.6) at As=1.11,Pr=0.068

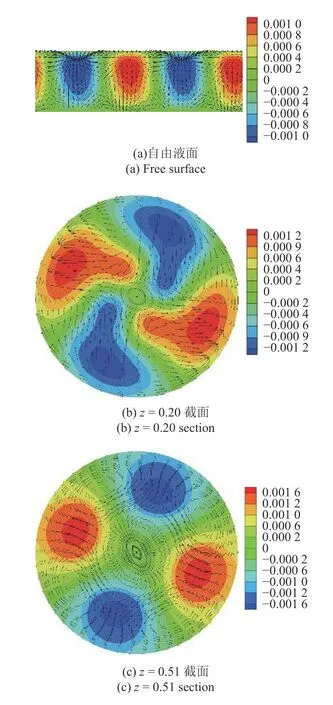
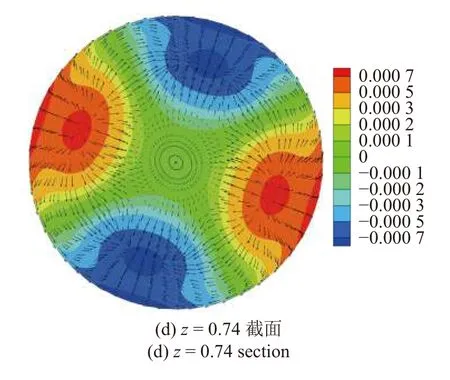
圖9 高徑比 As=1.11，Pr=0.068 的臨界狀態(Mac=1273.6)下擾動溫度(云圖)和擾動速度矢量(箭頭)Fig.9 The disturbance temperature (colored contour) and disturbance velocity vector (arrow) under the critical condition (Mac=1273.6) for the case of As=1.11 and Pr=0.068

2.3.2 失穩模式II (靜態失穩)

根據表4 可知,在1.20≤As≤2.50 區域內,失穩臨界頻率等于零,表示在這一高徑比范圍內,熱毛細對流從二維軸對稱定常對流失穩變為三維定常對流.隨著高徑比的增加,失穩的臨界波數kc=2 轉變為kc=1.由表5 和圖3 可知,液橋的流動失穩依然是由IV項主導,這表明失穩模式II 仍然是水動力學慣性失穩機制主導,其中M 項在失穩中的占比隨高徑比的增加先增大,再減小最后再增大(圖3(a)).在失穩模式II 中IV4和IV5是引起液橋流動失穩的主要原因,但在不同的高徑比下 IV4項和IV5項的占比存在差異.在1.20≤As≤1.54 范圍內,液橋的流動失穩是由IV4項主導(約占43%),但IV5項對失穩的貢獻同樣較大(約占28%),M 項的占比在13.39%～22.18%;在1.67≤As≤2.50,IV4項對失穩的貢獻增大,而IV5項和M 項的在失穩中的占比減小,同時IV2和IV3變為負值,所以IV4項是引起流動失穩的主要原因.下面對失穩模式II 進行具體分析.

在1.20≤As≤1.54 范圍,失穩臨界波數kc=2.根據圖10(a)所示,IV4和IV5是造成流動失穩的主原因,即基態軸向速度的徑向梯度和軸向梯度為引起失穩的擾動動能傳遞了主要的能量,其中IV4項比IV5項的貢獻更大,Mz和Mφ項在流動失穩中的占比也相對較大.流動失穩最危險的位置出現在液橋中部偏上附近并靠近自由液面處(圖10(b)).從自由液面展開圖(圖11(a))可知,擾動速度在靠近冷壁處是由熱極指向冷極,在熱壁附近則是由冷極指向熱極,這與圖12 所示的低普朗特數(Pr=0.009)液橋在自由液面處擾動速度的指向不同,在低普朗特數液橋中自由有液面的擾動速度都是從冷極指向熱極,且失穩都是水動力學慣性機制作用下的失穩,熱毛細機制對失穩沒有貢獻.由圖11(b)～圖11(d)可知,z=0.20 截面處擾動溫度的特征為:靠近自由液面R/3 形成強斑,截面處的擾動速度由冷極流向熱極;在z=0.51 截面處,擾動溫度特征為:在自由液面R/3 形成橢圓形強斑,并衍生出來的弱斑向自由液面靠近,截面處的擾動速度在靠近對稱軸處是由熱級指向冷極,在靠近自由液面附近是由冷極指向熱極;在z=0.74 截面處,擾動溫度特征為:擾動溫度強斑向自由液面靠近,截面處的擾動速度是由熱極流向冷極.

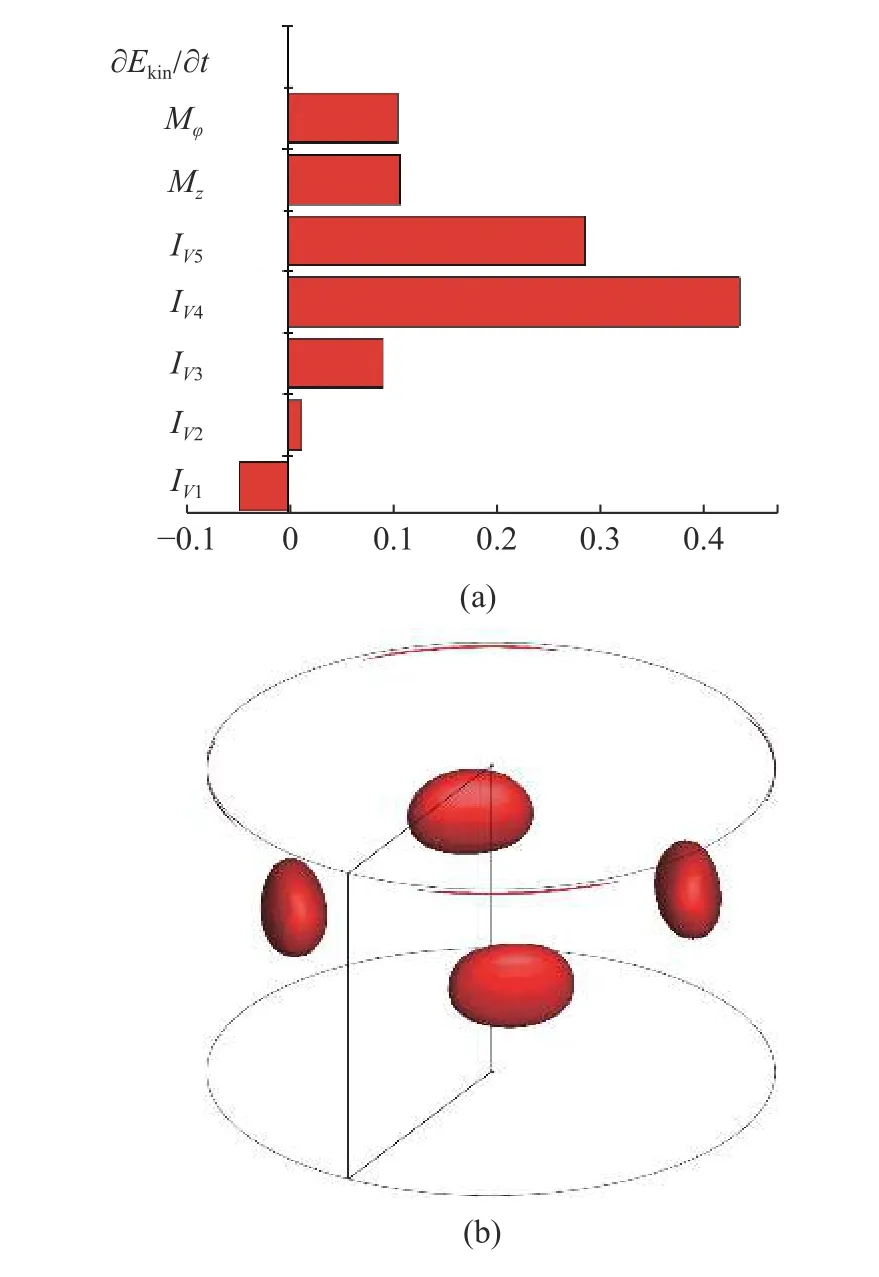
圖10 高徑比As=1.43,Pr=0.068 的臨界狀態 (Mac=531.9) 下:(a)擾動能量平衡條狀圖,(b) 局部擾動動能極值圖Fig.10 (a) The disturbance energy balance and (b) distribution of the local disturbance kinetic energy extreme value under critical condition(Mac=531.9) at As=1.43,Pr=0.068

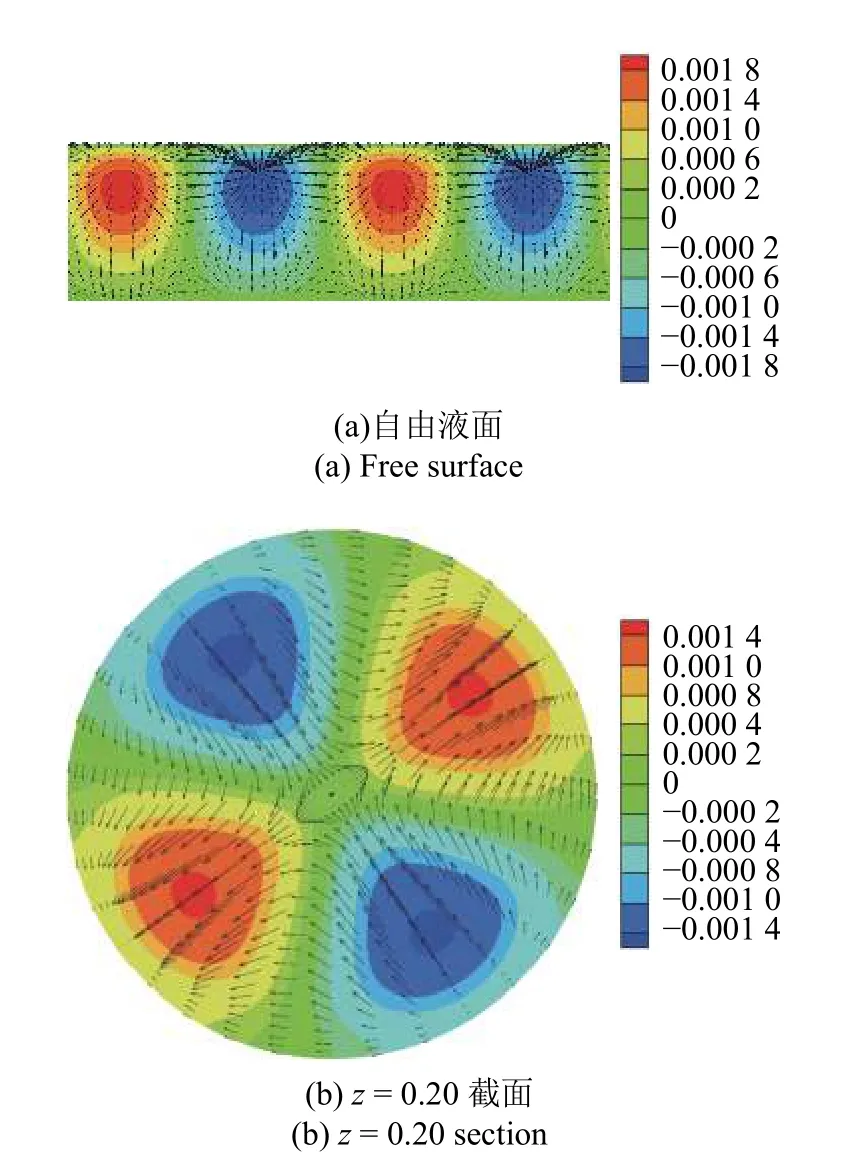
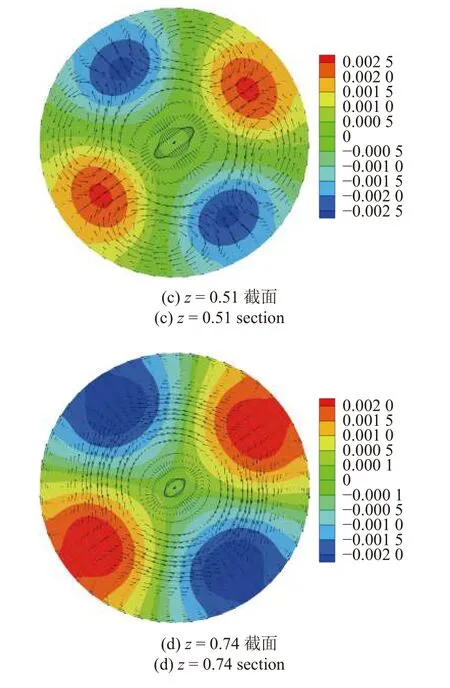
圖11 高徑比As=1.43,Pr=0.068 的臨界狀態(Mac=531.9)下擾動溫度(云圖)和擾動速度矢量(箭頭)Fig.11 The disturbance temperature (colored contour) and disturbance velocity vector (arrow) under the critical condition (Mac=531.9) for the case of As=1.43 and Pr=0.068

圖12 高徑比As=1.43,Pr=0.009 臨界狀態(Mac=531.9)下自由液面處擾動溫度(云圖)和擾動速度矢量(箭頭)Fig.12 The disturbance temperature (colored contour) and disturbance velocity vector (arrow) at the free surface under the critical condition(Mac=531.9) for the case of As=1.43 and Pr=0.009

在1.67≤As≤2.50 區間內,失穩臨界波數kc=1.由圖13(a)可知,IV4是造成流動失穩的主要原因,即基態軸向速度的徑向梯度為流動失穩提供了最主要能量,而Mz也對液橋的流動失穩有所影響,這表明失穩仍然是由水動力學慣性機制主導,同時熱毛細機制對失穩有所影響.與上述所有失穩機制不同的是,在該高徑比范圍內Mφ項起抑制流動失穩的作用.由圖13(b)可知,最危險的失穩位置出現在液橋中部并靠近自由液面.在圖14(a)中,擾動速度在靠近液橋冷壁處是由熱極指向冷極,在靠近液橋熱壁處擾動速度從冷極指向熱極,在1.05≤As≤1.18 和1.20≤As≤1.54 這兩個高徑比范圍內都曾出現這一現象,但在該高徑比范圍內這一現象更加明顯,擾動速度更多地從冷極指向熱極.由圖14(a)和圖15 對比分析可知,低普朗特數(Pr=0.009)液橋自由液面的擾動速度是從冷極指向熱極,這與GaAs 熔體液橋自由液面的擾動速度指向不同,由圖14(b)～圖14(d)可知,在z=0.20,z=0.51,z=0.74 的橫截面的邊緣處,擾動速度都是從冷極指向熱極,同樣驗證了自由液面處擾動速度更多的是從冷極指向熱極;這三處橫截面的擾動溫度特征為:隨著z 坐標的增大,擾動溫度強斑逐漸向自由液面靠近.

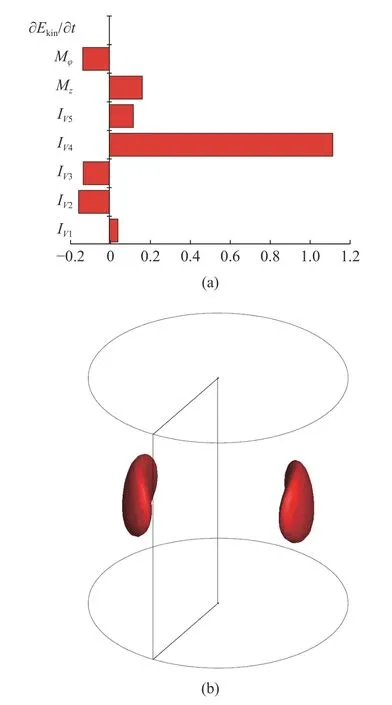
圖13 高徑比 As=2.00，Pr=0.068 的臨界狀態 (Mac=234.6) 下:(a)擾動能量平衡條狀圖,(b)局部擾動動能極值圖Fig.13 (a) The disturbance energy balance and (b) distribution of the local disturbance kinetic energy extreme value under critical condition(Mac=234.6) at As=2.00,Pr=0.068

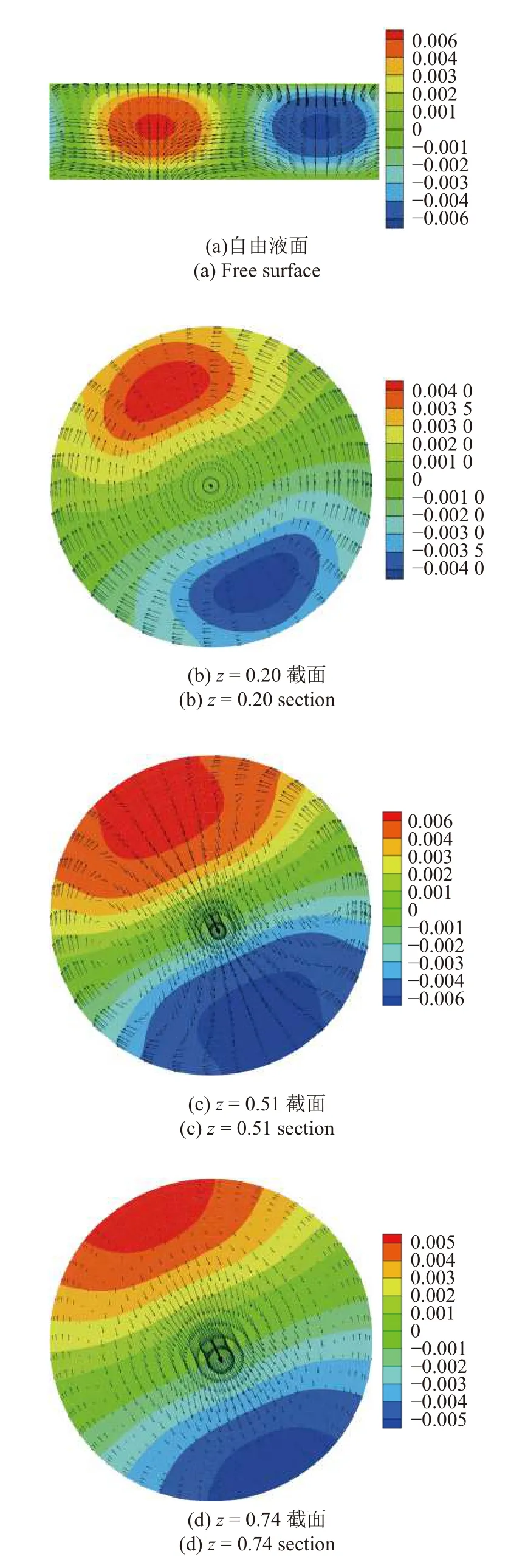
圖14 高徑比As=2.00,Pr=0.068 的臨界狀態(Mac=234.6)下擾動溫度(云圖)和擾動速度矢量(箭頭)Fig.14 The disturbance temperature (colored contour) and disturbance velocity vector (arrow) under the critical condition (Mac=234.6) for the case of As=2.00 and Pr=0.068

圖15 As=2.00 Pr=0.009 時臨界狀態(Mac=234.6)下自由液面處擾動溫度(云圖)和擾動速度矢量(箭頭)Fig.15 The disturbance temperature (colored contour) and disturbance velocity vector (arrow) at the free surface under the critical condition(Mac=234.6) for the case of As=2.00 and Pr=0.009

2.3.3 基態流函數和溫度分布

由圖16 和圖17 可知,在失穩模式I 和失穩模式II 中,隨著高徑比的增大基態渦胞的位置始終靠近自由液面附近.從圖16 和圖17 可以看出,當高徑比較小時,溫度場在靠近自由液面R/3 處向熱壁處擠壓,同時溫度場也在自由液面處向冷壁處擠壓,從而形成較大溫度梯度;但隨著高徑比增加,這種溫度場的擠壓相對減緩,從而隨著高徑比的增加溫度場沿軸向分布相對均勻.

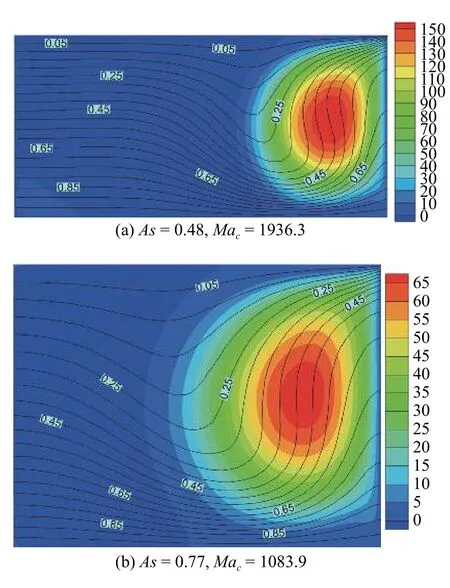
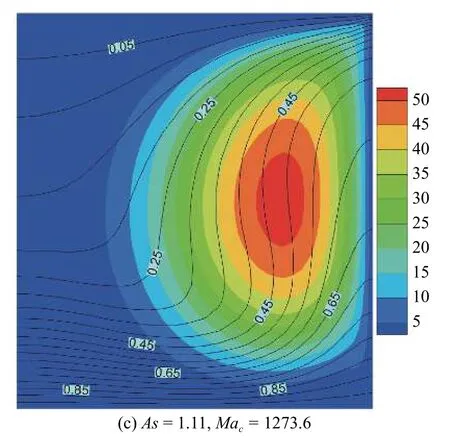
圖16 失穩模式I 在臨界狀態下的基態流函數(云圖)和基態溫度場(等值線)Fig.16 The basic flow (colored contour) and temperature (isotherm) of instability mode I under critical condition

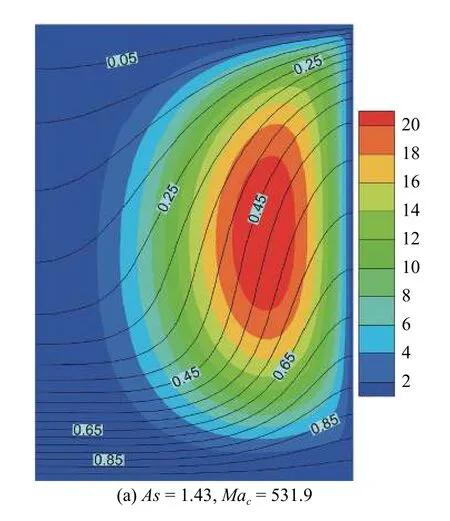
圖17 失穩模式II 在臨界狀態下的基態流函數(云圖)和基態溫度場(等值線)Fig.17 The basic flow (colored contour) and temperature (isotherm) of instability mode II under critical condition

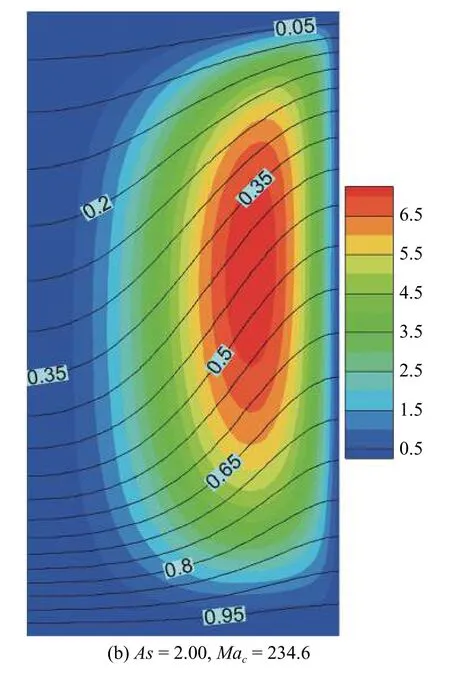
圖17 失穩模式II 在臨界狀態下的基態流函數(云圖)和基態溫度場(等值線) (續)Fig.17 The basic flow (colored contour) and temperature (isotherm) of instability mode II under critical condition (continued)

3 結論

基于已有文獻可知,液橋模型中熔體普朗特數對熱毛細對流失穩機制和失穩模式具有重要影響:對典型高普朗特數熔體(例如Pr＞1),熱毛細對流第一次失穩是從二維軸對稱定常對流轉變三維周期性振蕩對流,其失穩機制是熱毛細失穩機制;對典型低普朗特數熔體(例如Pr=0.011),熱毛細對流第一次失穩是從二維軸對稱定常對流轉變為三維定常對流,失穩機制是水動力學慣性失穩.同時文獻工作顯示液橋高徑比對熱毛細流對流的失穩臨界參數具有重要影響,但是未發現高徑比會影響熱毛細對流失穩機制和失穩模式(三維靜態失穩和三維振蕩失穩).

本文在基于譜元法線性穩定性分析對GaAs 熔體(Pr=0.068)液橋熱毛細對流研究發現,在同一普朗特數不同高徑比的情況下,隨著高徑比的改變液橋出現兩種失穩模式:當0.4≤As≤1.18 時,熱毛細對流是由二維軸對稱定常對流直接轉變為三維周期性振蕩對流(振蕩失穩);當1.20≤As≤2.5 時,熱毛細對流是由二維軸對稱定常對流轉變為三維定常流動(靜態失穩).基于能量分析我們發現,GaAs 熔體液橋的熱毛細對流失穩是由水動力學慣性機制占主導,兩種機制(水動力學慣性機制和熱毛細機制)共同作用造成.兩種機制對失穩的貢獻隨著高徑比的變化而變化,其失穩現象更加復雜,從而隨著高徑比的改變出現了兩種不同的失穩模式.由IV項各項的占比可知,IV4和IV5是造成流動失穩的主要原因,即基態軸向速度徑向梯度和軸向梯度為擾動場的失穩轉遞了主要的能量.在失穩模式I(振蕩失穩)中,最危險的失穩位置出現在熱壁附近,并隨著高徑比的增加逐漸向對稱軸靠近;在失穩模式II(靜態失穩)中,最危險的失穩位置液橋中部橫截面并靠近自由液面附近.