單元整合視角下數學教學內容的審視、梳理與設計

摘 要 “多邊形的面積”是人教版《數學》五年級上冊第六單元的內容，是在認識了基本平面圖形的特征，長方形、正方形的周長、面積，面積單位后學習的內容，是研究圓面積的基礎，也為研究長方體、正方體、圓柱圓錐體積提供策略依據。通過審視單元主題，梳理核心概念和單元目標，重組單元內容和練習，可以打破課時邊界，使知識學習系統化、知識內容結構化，方法遷移正向化，思維提升顯著化。

關? 鍵? 詞 單元整合 單元主題 核心概念

引用格式 宋健健.單元整合視角下數學教學內容的審視、梳理與設計[J].教學與管理，2022（08）：35-39.

小學數學知識內容往往具有關聯性和延續性，因此，現行小學數學教材的編排多是以單元為結構呈現的。根據不同的分類方式，可以將小學階段的數學單元分為內容單元、學科素養單元、項目單元等。而單元內部的各個組成部分都致力于說明某一方面的內容，或用相近的策略解決問題。因此，結合教材編排和學生特點，以整體化的視角縱觀單元內容，架構整體性、關聯性、層次性的單元整合教學，能幫助學生構建完整的知識體系，促進知識、策略方法的滾動式發展。然而，很多數學課堂上存在碎片化、淺顯化、無序化的單一課時教學，割裂了知識內容的起源，忽視了思維方式、策略方法之間的聯系，造成學生探究過程不到位、遷移轉化不明顯，思維提升不顯著等現象。那么，如何在單元整合視角下構建單元教學，筆者以人教版《數學》五年級上冊“多邊形的面積”為例，談談自己的若干思考。

一、審視單元主題，明確素養目標

單元是數學學習的內容和組織單位，單元主題是學習結構化的價值所在。而學生的學習過程離不開教師對教材的整體解讀，以及對單元素養目標的整體設計，因此，需要教師明確單元主題在整冊以及整套教材中的地位，對單元學習目標進行整體性規劃。從而幫助學生理解所學單元的本質，并在實現遷移的過程中理解知識內容、策略方法和思維方式之間的聯系。

1.著眼全局，分析溝通

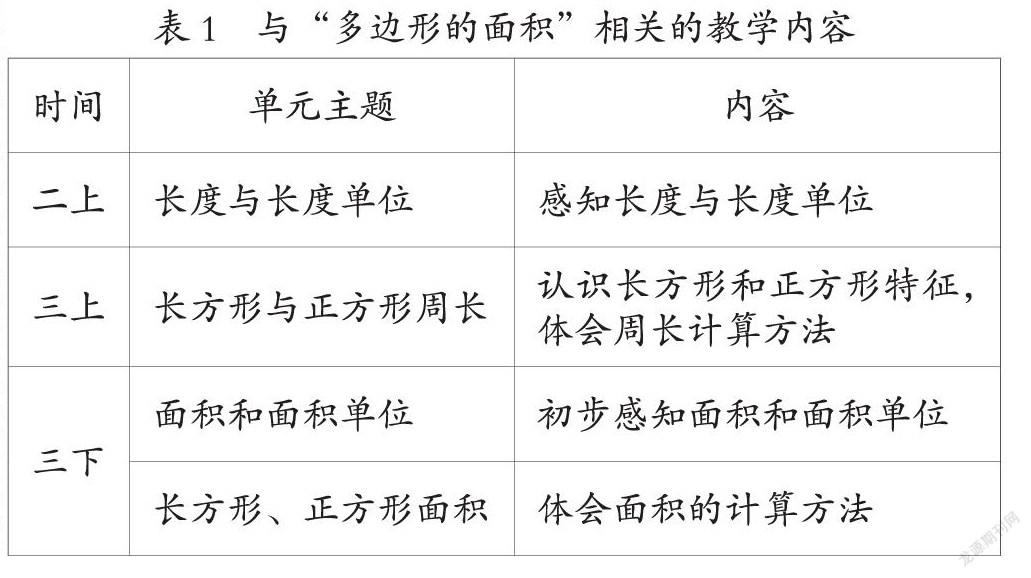
奧蘇伯爾認為：“學習的實質就是學生認知的組織和重新組織，組織和重新組織的過程就是新舊知識相互聯系、相互作用的過程。”由此可見，需要仔細研讀課程標準、教材，明確單元教學目標以及教材體系，分析“多邊形的面積”在教材體系中所處的位置，以及在核心素養培養活動中所處的地位，借助新舊知識之間的聯系，將新知嵌入原有知識體系。與“多邊形的面積”相關的內容在各冊教材中的編排見表1：

“多邊形的面積”是學生在生活與學習中積累了圖形認識、測量等經驗，理解了面積意義、面積單位，了解了長方形和正方形的周長和面積以及平移和旋轉等知識后編排的，是探究組合圖形面積的基礎[1]。同時，這一單元內容的結構化學習經驗，將為探究圓面積轉化為相似長方形提供方法指導，也將為圓柱、圓錐體積轉化成長方體和正方體提供策略轉化的經驗。

2整體架構，明確目標

本單元例題的探究始終圍繞“轉化—推導—應用”展開。通過整體設計單元目標，幫助學生積累平行四邊形轉化成長方形的經驗，并將這一經驗遷移到后續內容的學習中去，實現知識和策略方法的雙提升。因此，本單元的教學目標可以整體確定為[2]：

1.通過思考、合作交流，將所研究的平面圖形轉化成已經學過的圖形。

2.探究多邊形與已學圖形之間的聯系，理解面積的計算方法，并能用數學語言進行描述，達到思維與表述的一致性。

3.能用多種方法推導面積公式，嘗試從不同角度思考問題，并能通過觀察，認識簡單組合圖形并正確地計算。

4.反思評價單元學習過程，總結提煉方法，并能進行有效拓展，提升元認知能力。

二、關注單元內容，提煉核心概念

在整體設計單元目標后，需要關注單元內容，分析單元核心概念，從而圍繞其開展教學。以數學核心概念為中心的單元整合教學設計，能幫助教師聚焦單元核心和要點，助力學生的數學“大觀念”，從而促進他們對數學知識本質的理解，實現學科內部知識的融會貫通和正向遷移，構建完善的自我認知體系和策略體系[3][4]。

1.關注本質，突破難點

核心概念主要指在概念體系中某些處于核心、樞紐位置的概念，一般對其下行概念或相關概念起著同化性遷移作用，包括起始概念、關系概念等，它是知識內容與素養之間的橋梁。教師基于核心概念的高視角架構，在新舊知識的沖突點、增長點、勾連點、思維創新點發現問題，梳理總結，從而給予學生正確認識與策略方法的引導，有助于知識體系的構建和策略方法的遷移。

“轉化思想”是本單元的核心概念，將平行四邊形面積轉化成長方形是基礎，但轉化成長方形的緣由是便于“度量”。對五年級學生而言，平行四邊形面積的轉化與推導過程難度不大，還有部分學生已經通過其他途徑了解了三角形和梯形面積的計算方法，但對面積推導過程并不了解，特別是三角形、梯形面積推導方法比較多，學生理解有一定的難度。由此，通過實踐操作，讓學生感悟面積計算的本質是“單位面積”的度量，從而轉化成已學過的圖形——長方形或平行四邊形，不失為突破單元難點的途徑。

2.厘清主次，促進遷移

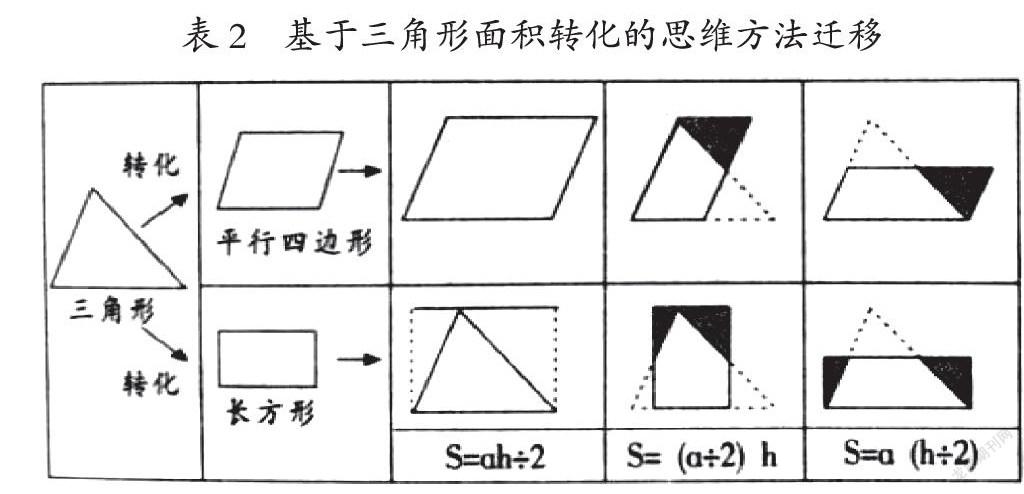
在關注單元核心概念的基礎上，厘清單元內容的主次，使學生實現無序認知到有序認知的過渡，將碎片化的知識內容學習策略串連成線、并聯成網，并實現立體化構體，形成清晰穩固的知識結構和策略體系，實現單元策略方法的正遷移。本單元中，平行四邊形面積的轉化是基礎，但三角形面積的轉化卻是關鍵。三角形面積可以轉化為等底等高的平行四邊形面積÷2，也可以轉化成一個長方形。不同學生采用的轉化方法并不相同，按照原來的課時編排，學生大都選擇用2個完全相同的三角形拼成平行四邊形，因為在學習三角形面積前已有豐富的轉化經驗，并且經歷了一堂練習課。但在單元整合設計后，學生的認知基礎是三年級的長方形、正方形面積，因此會有一部分學生選擇將三角形轉化成長方形。不管哪種方法最后都歸結到公式ah÷2。將基于三角形本質特征的轉化思想加以分類歸納，可以幫助學生將類似的思維方法遷移到梯形面積的公式推導中，實現結構化學習。

三、梳理單元結構，重組重點課例

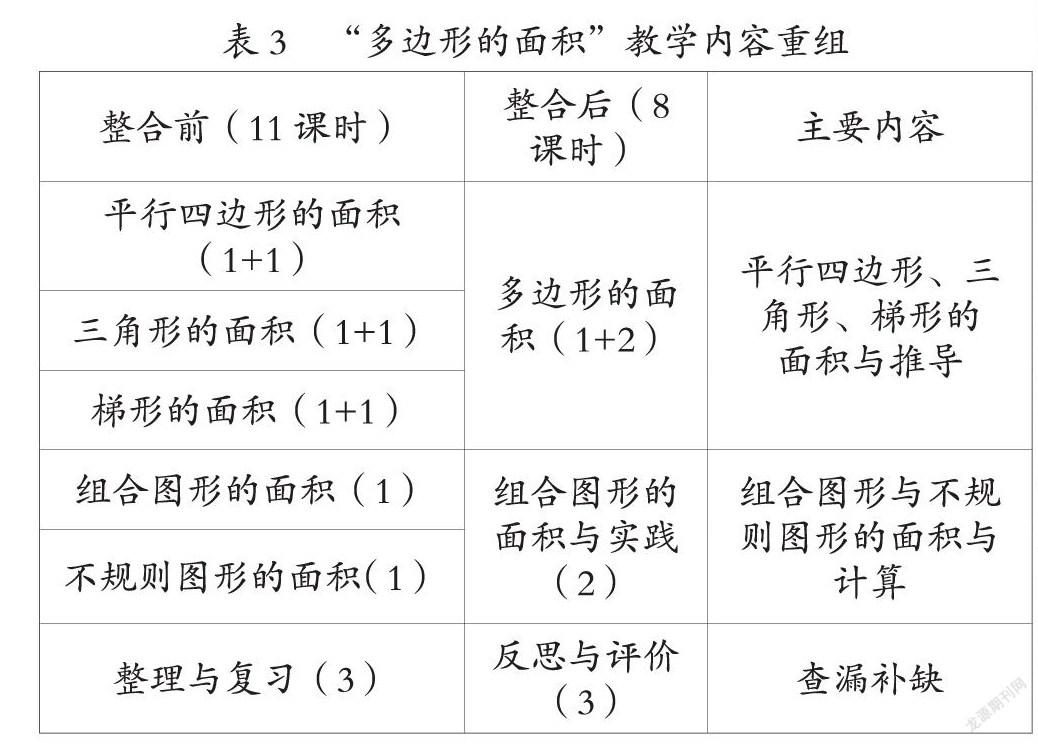
無論是以哪種單元核心概念，何種素養目標開展單元教學，其具體實施總是以“課”為主要時間單位展開的。因此，需要教師根據單元目標和單元核心概念準確把握知識間的聯系、精心梳理內容結構，將單元內容進行必要的重組與調整，特別是開發和重組重點課例，增補相關課時，需要進行連續的、有指向性的單元教學，從而創設真正適合學生研究的學習方式。因此，筆者從度量與轉化這兩個維度，對本單元進行了整合重組，將原來的11課時整合成8課時（見表3）。

1.設計重點課例

每個單元的起始課都將開啟單元學習的起點，起到提綱契領的作用。因此，需要教師俯瞰整個單元，從內容、策略方法兩方面對整個單元進行整體設計，形成統一、連續的方法指導。本節課將數面積單位作為核心，以方格紙為主要探究材料，將面積的推導過程作為主要探究活動，幫助學生理解轉化與度量的本質。

環節一：回憶度量，溝通舊知。

師：回憶一下，我們學過哪些關于度量的知識？（用尺量物體的長度，量角的度數，面積的度量……）

師：長方形的面積是怎么研究出結論的？（數格子，每行有幾個乘幾行）

師：就是數一數共有幾個1平方厘米的格子。

師：回憶一下長方形和正方形的面積公式（正方形的面積=邊長×邊長，長方形的面積=長×寬）。

環節二：任務驅動，自主探究。

師：請你想辦法求出下面圖形的面積，并表示出來。

反饋交流問題一： 你覺得求哪些圖形的面積最簡單？（長方形）

師：長方形的面積是怎么研究出結論的？（數格 子，每行有幾個乘幾行）

師：回憶一下長方形的面積公式。（長方形的面積 = 長 × 寬）

反饋交流問題二：你覺得求哪些圖形的面積最困難？（圓和葉子）

師：展示學生想法，誰看明白了？這樣能精確地數出來嗎？

師小結：看來面積的計算就是數一數有幾個面積單位。圓的面積將在六年級探討，今天我們重點研究平行四邊形、三角形和梯形的面積。

師：可以用什么辦法求出平行四邊形、三角形和梯形的面積？請你用數一數、畫一畫、剪一剪等方法求出這三個圖形的面積，并在小組內交流。

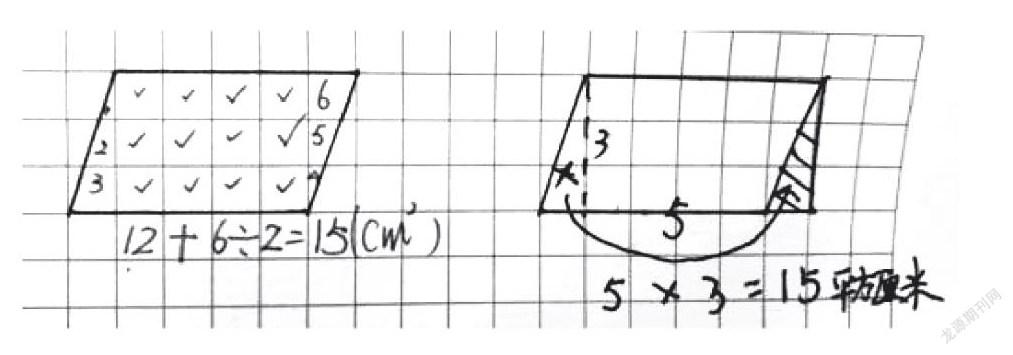
（1）平行四邊形的面積。

呈現學生的方法，并說說是怎么想的。

師：兩種方法都可以。對比一下，哪種方法更簡便，為什么？

生：右圖，因為移動后變長方形了，每行5格乘3行就是15m2。

師：你想到了長方形的面積計算方法，那么平行四邊形面積可以怎么算？

生：平行四邊形的面積=底×高

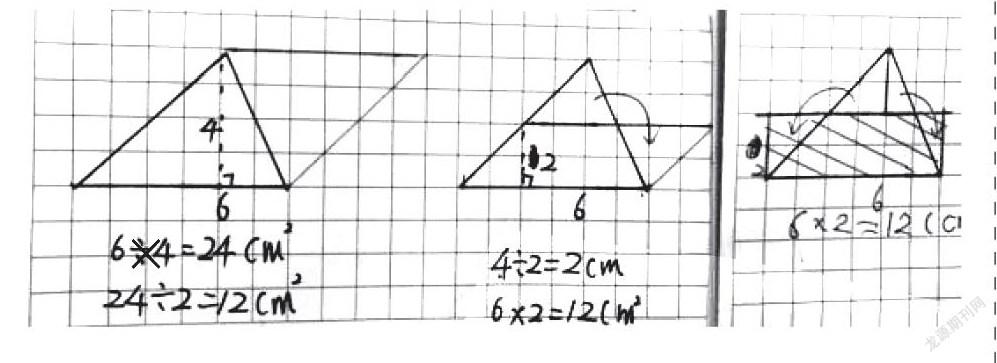
（2）三角形的面積。

展示學生的幾種想法。

師：你看懂了哪種想法？

生：第一種是用2個完全相同的三角形拼成平行四邊形，4×6÷2=12cm2;第二種也是變成平行四邊形，不過高是一半就用4÷2=2cm，6×2=12cm2;第三種是變成長方形，高4÷2=2cm，6×2=12cm2。

師：為什么都要÷2？

生：因為第一種想法中三角形面積是平行四邊形面積的一半;第二種和第三種想法在移動后，底不變，高是原來高的一半，所以也要除以2。

小結：三角形的面積 =? 底× 高 ÷2

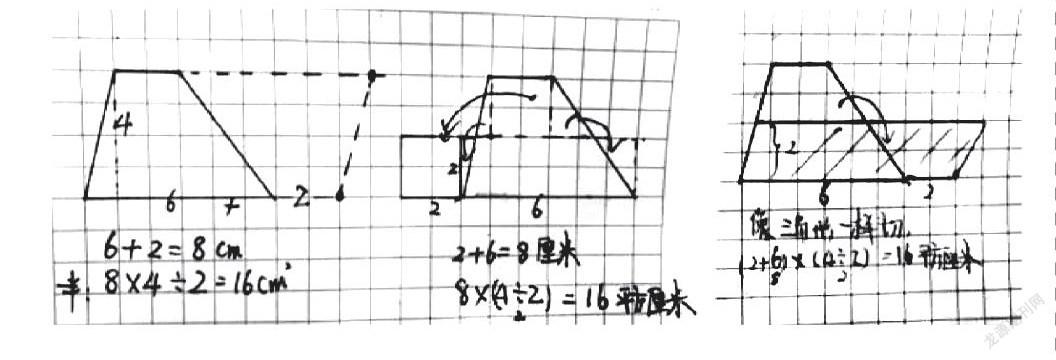
（3）梯形的面積。

呈現學生的幾種方法：

師：你看懂了哪種想法？是怎么想的？

生：第一種是用2個完全一樣的梯形拼成平行四邊形，底×高÷2;第二種是變成長方形，長就是上底+下底，但高是4÷2=2cm，8×2=16cm2;第三種有點像上面三角形的方法，高變成一半，所以也÷2。

師：對比三種方法，你更喜歡哪種？為什么？

生：第一種，因為看起來更清楚。

小結：梯形的面積=（上底+下底）×高÷2

環節三：對比小結，歸納公式。

師：觀察剛才的3個面積計算公式，大家有什么發現？

生：3個面積計算公式都包含底×高。

師：梯形的底是指什么？

生：上底+下底

師：底和高分別表示什么？

生：底表示每行有幾個，高表示有幾行。

師：為什么三角形和梯形的面積要除以2？

生：因為三角形、梯形的面積是由2個相同的圖形拼起來的。

師：回顧一下整個探究過程，有什么相同點？

生：平行四邊邊形、三角形和梯形的面積都可以轉化成長方形計算。

環節四：知識鏈接，促進勾連。

師：求面積就是求幾個面積單位的和，轉化成長方形或者平行四邊形是為了方便數，計算公式其實是簡單數法。除了面積、長度的疊加，還有其他的疊加情況嗎？（體積、角度、時間、重量、計數單位……）

從回憶學生熟悉的長度、周長的度量引入單元主題“度量”，喚醒學生的已有經驗，到不規則圖形“葉子”面積的度量就是數有幾個面積單位，初步感知求面積的方法，即計算面積就是數圖形里有幾個面積單位，從而便于學生將方法遷移到其他基本圖形中。教師將平行四邊形、三角形、梯形面積探究過程整合到一起，以大任務驅動學生自主探究方法，由于有了前面的數方格經驗，學生基本能想到轉化成長方形和平行四邊形去度量。

教師在整個探究過程中設計了4個層層遞進的問題：（1）教師在求每個圖形面積的最后提問“哪種方法更簡便？”使學生思考“零碎數”“整塊數”“轉化成已學過的圖形”哪種更簡便。（2）探究完三個圖形的面積后加入公式的提煉與提問：“觀察3個面積計算公式，你有什么發現？”使學生結合圖形從結構與形式上觀察它們的相同點，都是底×高，但三角形和梯形面積還要÷2，追問“為什么？”，促使學生思考面積的本質，即每行幾個×幾行。（3）再提問整個過程有什么相同點，注重面積推導過程之間的聯系與溝通，構建完整的面積計算方法和轉化策略的橫向脈絡。（4）“除了面積、長度的疊加，還有其他的疊加情況嗎？”通過回憶其他度量內容，啟發學生發現以度量為核心的縱向知識鏈接，構建縱橫交錯的完整體系。

2.增補知識內容

在數學學習過程中，單元整合教學與對應的練習設計是學生學習活動的重要保障。由于將原本3個課時的新授內容整合為一個課時，學生的策略方法遷移較深入，但難免使每個圖形面積的變式練習較為薄弱。因此，可以將節省出來的課時重新設計安排，比如結合關鍵課例增補相關知識內容，重新設計單元練習，促進思維的提升。

例如新授課后，針對平行四邊形、三角形和梯形的面積，可以設計以下幾個層次的練習：

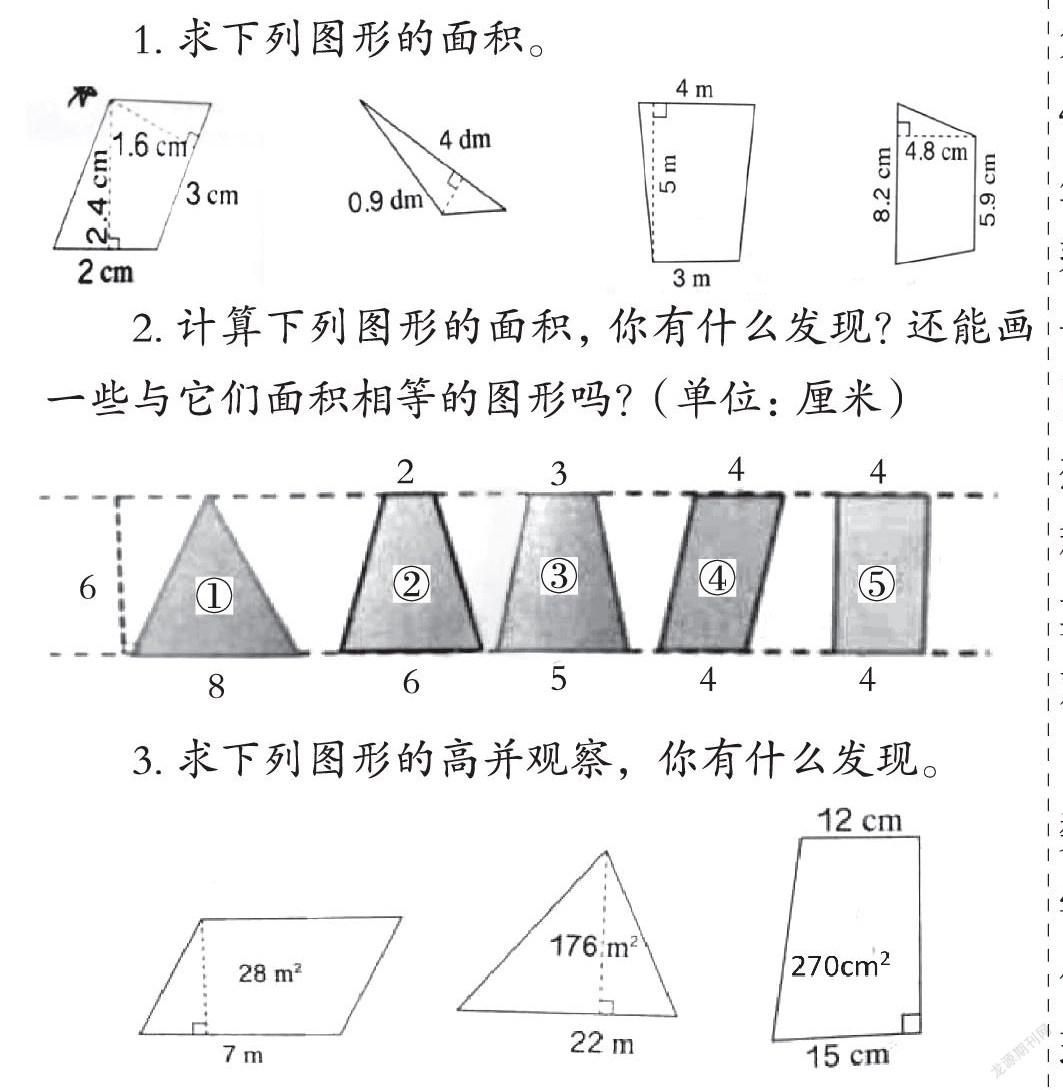
1.求下列圖形的面積。

2.計算下列圖形的面積，你有什么發現？還能畫一些與它們面積相等的圖形嗎？（單位：厘米）

3.求下列圖形的高并觀察，你有什么發現。

4.對比觀察，有什么發現？

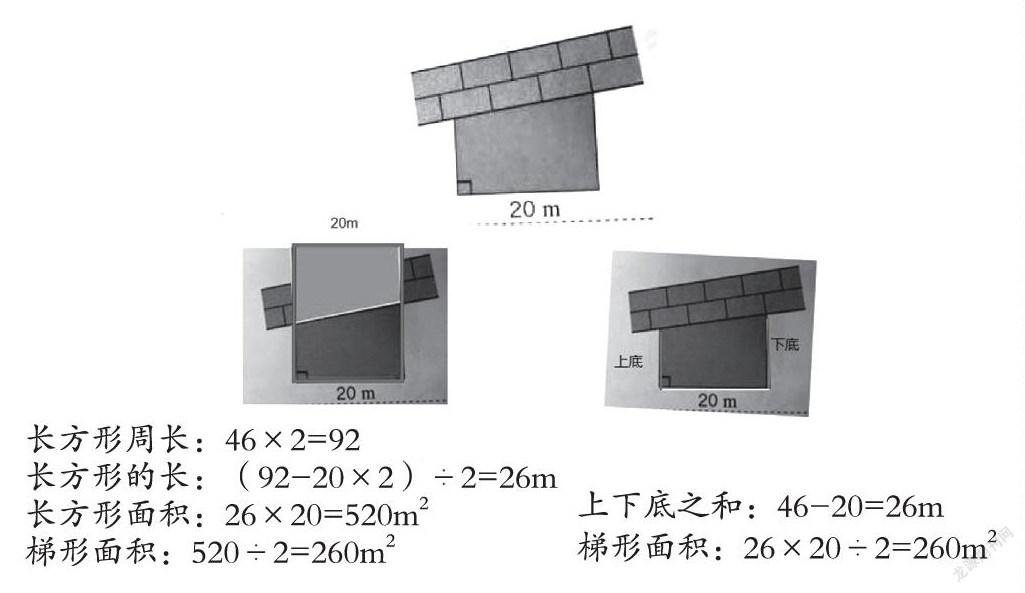
靠墻邊的一個梯形花壇，圍花壇的籬笆長46米，求這個花壇的面積。如果每盆花占地0.5平方米，這個花壇共放多少盆花？

教師呈現學生的方法，并出示圖片：

單元整合后的多邊形面積第二課時設計了四個層次的練習：練習1主要鞏固平行四邊形、三角形和梯形面積的基本計算方法，其中平行四邊形練習還滲透了底和高一一對應的內涵，梯形圖旨在先辨析上下底與高，再計算;第二個練習分兩個層次，先是通過計算發現圖中的長方形、平行四邊形、三角形、梯形的面積相等，即都可以轉化成底為4厘米，高為6厘米的長方形或平行四邊形，再讓學生畫一畫與它們面積相等的圖形，既能發散學生的思維，又滲透等積變形的思想;第三個練習是已知面積和底求高，通過類似的三題，使學生發現已知三角形或梯形高時，可以先×2轉化成平行四邊形面積，再÷底就是高，打通三角形、梯形面積與平行四邊形面積之間的壁壘;練習4是聯系生活實際的解決問題，通過數形結合促進學生理解上下底之和這一整體性概念，再用上下底之和乘高÷2求面積，突破梯形面積計算中上下底之和這一難點。這樣的單元整合式作業既復習了基本平面圖形的面積計算方法，又滲透了等積變形以及轉化思想，也為后續研究圓面積的推導，圓柱的體積推導過程提供了策略依據，為打通一維、二維、三維間的壁壘奠定基礎，從而構建學生的圖形結構框架，發展空間觀念。

總之，單元視角下的“多邊形的面積”教學，是以數學課程標準為指導，以整合思想為核心的課程與教學的結合，能幫助學生實現量的疊加到知識方法結構化的飛躍。以整體性、聯系性視角審視單元主題，梳理單元內容與結構，重組重點課例，建構起“聯系—循環”的教學方式，促進學生整體認知結構的發展，提高自主學習的能力，提升數學核心素養。

參考文獻

[1] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[2] 陳慧蓉.重組“四類”結構，提升大單元教學實效[J].福建教育，2021（27）：48-51.

[3] 陳云.深度學習觀下的小學數學單元整體教學——以蘇教版五上“多邊形的面積”單元教學為例[J].小學數學教師，2021（09）：56-59.

[4] 胡曉敏.單元“大概念”的提取策略[J].教學月刊·小學版：數學，2020（12）：30-32.

[5] 胡曉敏.大概念視角下的單元教學設計實踐與價值[J].小學教學參考，2021（29）：23-25.

[責任編輯：陳國慶]

3535501908210