“證據推理與模型認知”化學學科核心素養的建構
——以兩道化學“數形結合型試題”的教學為例
杜德祥
(昆明市第一中學,云南 昆明 650031)
《普通高中化學課程標準(2017年版2020年修訂)》中明確指出,學科核心素養是學科育人價值的集中體現,也是學生通過學科學習而逐步形成正確價值觀、必備品格和關鍵能力的目的。化學學科核心素養包括“宏觀辨識與微觀探析”“變化觀念與平衡思想”“證據推理與模型認知”“科學探究與創新意識”“科學態度與社會責任”5個方面[1]。本文就“證據推理與模型認知”作一些思考,探究在高中化學教學中,如何以數形結合型試題為載體,培養學生模型認知的能力。
1 數形結合思想概述
數形結合思想就是把抽象的數學語言、數量關系,跟直觀的圖形、位置關系,結合起來的思維方法。近年來的高考化學試題中數形結合型試題都有所涉及。教學中充分利用此類試題,培養學生“證據推理與模型認知”的核心素養具有重要意義。
2 數形結合型試題解題分析
“模型”包括實物模型和非實物的形式模型兩類。形式模型又包括數學模型、圖像模型和語義模型。圖像模型是用二維或三維坐標系中的數學圖像描述的模型。模型認知能力主要包括建立模型(建模)和運用模型(用模)兩個方面。建模是用模的前提,用模是建模的目的。
本文以兩道各具特色的“數形結合型試題”的教學為例,探究在實際教學活動中,如何培養學生的模型認知能力。
2.1 2021年全國理科綜合甲卷(第12題)
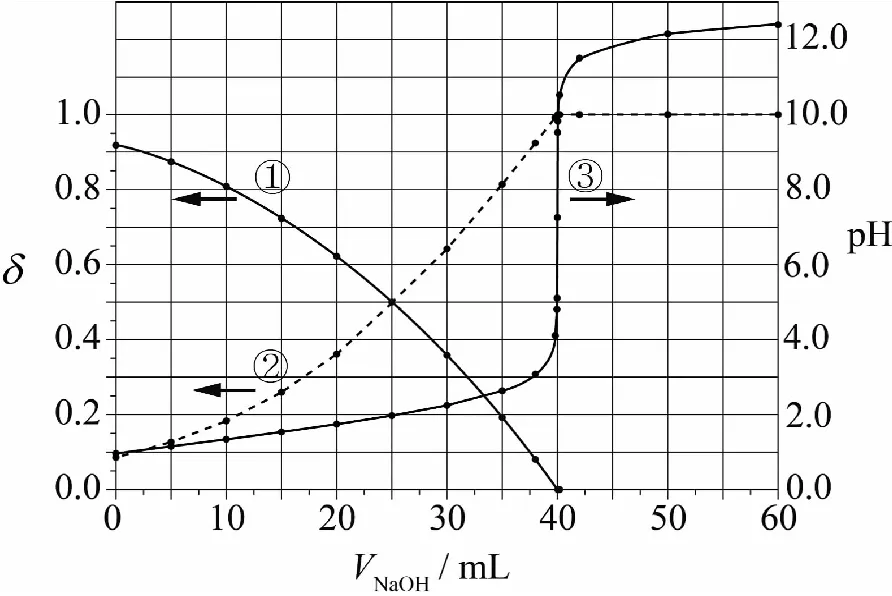
已知相同溫度下,Ksp(BaSO4) A.曲線①代表BaCO3的沉淀溶解曲線; B.該溫度下BaSO4的Ksp(BaSO4)值為1.0×10-10; C.加適量的BaCl2固體可使a點變到b點; D.c(Ba2+)=10-5.1時兩溶液中c(SO42-)/c(CO32-)=10y2-y1。 本題考查的是沉淀的溶解結晶平衡,難度較大。能根據圖示準確判斷兩條曲線各自所代表的物質是解題的關鍵,根據溶度積常數進行計算是本題的難點。命題情境除了傳統的考查溶度積常數的意義、性質、表達、應用及相關計算外,呈現的題型則是將非線性方程的溶度積常數表達式,以圖像為載體,進行線性化處理的考查方式。 解題模型為:首先,要深刻理解溶度積常數的本質內涵,掌握其意義、性質、表達、應用及相關計算;其次,要研究根據數學知識進行線性化處理的方法。 2.1.1 建立模型 建立模型是學生“模型認知能力”的基礎,教學中要引導學生并不斷強化首先要建立兩個模型。 1)數學模型 a)坐標系中橫坐標和縱坐標的物理意義。橫坐標表示-lg[c(Ba2+)],根據數學知識可推理得,橫坐標的值越大,c(Ba2+)越小;縱坐標表示-lg[c(SO42-)]或-lg[c(CO32-)],同理可推理得,縱坐標的值越大,c(SO42-)或c(CO32-)越小。b)關注“點”:起點、終點、轉折點、拐點、交點等的意義。c)關注“線”——變化趨勢。 2)化學模型 2.1.2 運用模型 1)收集證據 對于A選項,當橫坐標即-lg[c(Ba2+)]為同一數值時,圖中曲線②對應的縱坐標的值總小于曲線①,即曲線②對應的離子濃度總大于曲線①。由于Ksp(BaSO4) 2)基于證據進行分析推理 對于B選項,由前述知,曲線①代表的是BaSO4的沉淀溶解曲線,即該曲線上的任意一點都滿足Ksp(BaSO4)=c(Ba2+)·c(SO42-)。這樣,可以取曲線①上的任意一點,如(1.0,9.0),則有-lg[c(Ba2+)]=1.0,-lg[c(SO42-)]=9.0,即c(Ba2+)=1.0×10-1.0,c(SO42-)=1.0×10-9.0。 所以Ksp(BaSO4)=c(Ba2+)·c(SO42-)=1.0×10-1.0×1.0×10-9.0=1.0×10-10.0。即B選項正確。 以上討論的是數形結合型試題中的一種類型——通過對中學化學中的各種常數(可逆反應的化學平衡常數、弱電解質的電離平衡常數、水解平衡常數、水的離子積常數以及難溶物質的溶度積常數)進行線性化處理,立足化學知識進行命題。對各種常數進行線性化處理是化工生產中常用的處理方法。全國高校化學工程專業的學生就要專門學習一門課程——化工數學,該課程的核心課題是利用數學知識去解決化工問題,包括化工實驗數學、化工過程模擬和優化等,其中就有專門的章節,探討數據的線性化處理。解答此類型試題的基本模型為:首先是深刻理解對各種常數進行線性化處理的本質原理,其次是深刻理解涉及到的化學知識的本質內涵,然后再根據題給信息搜集證據、分析推理,解決問題。 以酚酞為指示劑,用 0.1000 mol·L-1的NaOH溶液滴定 20.00 mL 未知濃度的二元酸H2A溶液。溶液中,pH、分布系數δ隨滴加NaOH溶液體積VNaOH的變化關系如下圖所示。 [比如A2-的分布系數: 下列敘述正確的是( ) A.曲線①代表δ(H2A),曲線②代表δ(HA-) ; B.H2A溶液的濃度為0.2000 mol·L-1; C.HA-的電離常數Ka=1.0×10-2; D.滴定終點時,溶液中c(Na+)﹤2·c(A2-)+c(HA-)。 本題將酸堿中和滴定過程中pH的變化曲線、酸根離子的分布系數融合在一起。考查電解質溶液的知識:判斷H2A的強弱及其第二級電離平衡常數、平衡常數的計算、溶液的電荷守恒及其應用。題給圖像屬于雙縱坐標曲線,是數形結合型試題的又一種命題形式。 2.2.1 建立模型 1)數學模型 a)pH=-lgc(H+);b)雙縱坐標系中分布系數δ看左邊縱坐標,滴定過程中溶液pH的變化看右邊縱坐標;橫坐標為滴入的NaOH溶液的體積。 2)化學模型 a)酸堿中和滴定過程中,溶液濃度的簡單計算;b)電離平衡常數的計算;c)溶液呈電中性的性質及其運用。 2.2.2 運用模型 1)搜集證據 由題給坐標系可知,加入的NaOH溶液的體積為 0 mL 時,溶液pH≈1;加入NaOH溶液的體積為 25.00 mL 時,曲線①和曲線②相交,即此時曲線①和曲線②分別代表的兩種微粒的分布系數δ相等,溶液的pH等于2.0(注意溶液pH的變化要看右邊縱坐標,即此時溶液的pH不等于5.0);加入NaOH溶液的體積為 40.00 mL 時,溶液pH發生突躍,達到滴定終點,溶質為Na2A。 2)利用證據進行分析推理 立足化學知識,以雙縱坐標系方式呈現,突出了數學語言的抽象性、概括性和簡約型。解題過程中形成思維的模型化即程式化,對于問題的解決可以起到事半功倍之功效。 同樣,利用以下試題,可以培養學生的“證據推理與模型認知”能力:1)2019年全國理綜I卷第11題、全國理綜II卷第12題、全國理綜III卷第28題(節選);2)2020年全國理綜I卷第28題、全國理綜II卷第26題(節選)、全國理綜III卷第28題(節選);3)2021年全國理綜甲卷第28題(節選)、全國理綜乙卷第13題和第28題(節選)。 在實際教學中,教師要培養學生模型認知的能力,要求教師要有強烈的“證據推理與模型認知”意識,深入理解并挖掘學科和試題中蘊含的核心素養的培養目標,指導實際教學。在教學設計中,要重視數學模型的功能與價值,引導學生再現數學知識和理論。同時,要引導學生運用化學基本知識及理論,逐步推理并建立跨學科知識間的聯系及應用模型,通過“建立模型——收集證據——基于證據分析推理(應用模型)——發展模型”的課堂活動主線,培養學生“證據推理與模型認知”的核心素養。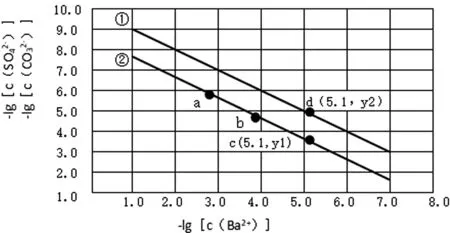



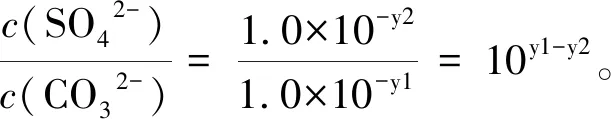
2.2 2020年全國理科綜合I卷(第13題)
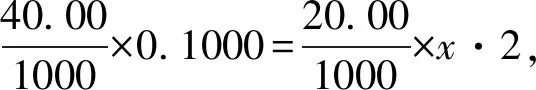
3 結語

