基于組合模型的金融機構存款余額預測研究
——以河南省為例

魏 敏

（鄭州大學 商學院，鄭州 450001）

一、引言

金融機構的主要功能是融通資金和匯集資本，金融機構存款余額指的是金融機構一段時間內的存款金額。隨著創新型存款產品的增多和大眾金融意識的增強，儲蓄熱度持續升高，研究金融機構存款余額發展趨勢，對制定宏觀經濟戰略、財政貨幣政策，指導金融部門運作與經營，保持國民經濟健康發展等具有重要的現實意義。

現有關存款余額預測的研究層出不窮，大多數的研究將其看作一種金融時間序列，研究方法則由線性模型向非線性模型、單一模型向組合模型預測過度。在眾多預測模型中，ARIMA模型得益于對序列線性擬合的有效性和短期預測的準確性最為流行。李明明分別利用ARIMA模型、季節指數預測模型以及兩者的組合對居民儲蓄存款進行預測，結果發現組合模型的擬合更為精確。除傳統計量模型外，更多的模型也廣泛應用于存款余額的預測。馮宇利用權重分配法來確定灰色模型、三次指數平滑模型和BP神經網絡模型預測方法的權重，建立了三者的組合預測對吉林省金融機構存款余額進行了預測，得到了較為準確的結果。由于現實中的金融時間序列存在不平穩、非線性的特點，傳統的計量模型和淺層神經網絡模型無法得到更為準確的預測結果。但是深度學習模型中的長短時記憶神經網絡（Long Short Term Memory，LSTM）通過非線性映射技術，可以有效地解決此類問題。Hochreiter提出了LSTM神經網絡后，其便廣泛應用于金融時間序列的預測，如股票指數、人民幣匯率、稅收等，均取得了較為理想的結果。

金融數據本身蘊含著豐富的信息，但是，單一模型無法全面地捕捉到序列背后的信息。為了更好地利用傳統計量模型與深度學習模型方法的優點，研究利用組合模型對河南省金融機構存款余額進行預測。首先介紹了ARIMA模型和LSTM模型的結構原理，在實證了ARIMA對存款余額線性部分擬合和LSTM模型預測存款余額非線性部分擬合的基礎上，通過構建組合模型，顯示了ARIMA-LSTM在預測存貸款余額上的優勢。

二、模型理論基礎

（一）ARIMA模型理論

在金融時間序列預測中，模型根據原序列是否平穩以及回歸中所含部分的不同，分為移動平均過程（MA）、自回歸過程（AR）、自回歸移動平均過程（ARMA）以及差分自回歸移動平均模型（ARIMA）過程。ARIMA模型的基本結構為不包括季節性因素的ARIMA（p，d，q）模型和包括季節性因素的ARIMA（p，d，q）（P，D，Q）模型。

在ARIMA（p，d，q）（P，D，Q）模型中，p、d、q分別表示自回歸階數、差分次數和移動平均階數，P表示季節性自回歸階次，Q表示季節性移動平均階次，D表示季節性差分階數，表達式如（1）所示。

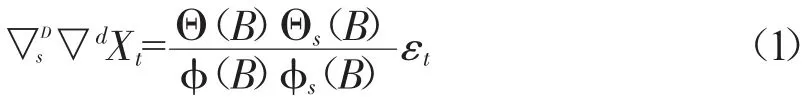
（二）LSTM模型理論

LSTM通過輸入門（inputgate）、遺忘門（forgetgate）和輸出門（output gate）對輸入的數據進行計算輸出。具體來說，輸入門和遺忘門分別控制新輸入值和當前單元狀態對新單元狀態的影響程度，表達式如（2）和（3）。其中，X是神經元的輸入，h是神經元的輸出，i是神經元輸入門的輸出，f是神經元遺忘門的輸出，b、b、b、b為權值矩陣，公式中的⊙表示哈達瑪（Hadamard）乘積，rec是修正線性單元（Rectified Linear Unit，ReLU）激活函數。表達式（4）中c～是更新的狀態，通過計算可以更新當前時刻接收到的數據。

細胞狀態負責跟蹤過去時刻的相關信息，公式（5）同時反映了有選擇地記住當前時刻的信息和有選擇地保留過去時刻的信息的過程。

O是神經元輸出門的輸出，輸出門如表達式（6）所示。輸出層將真實值與預測值進行比較得到誤差函數，根據誤差函數修正后便可以得出最終的輸出部分。

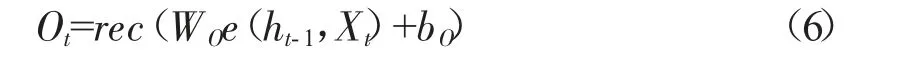
通過以上步驟，LSTM便能夠通過調整各個控制門的權重對其相應的輸入數據進行訓練而得到，進而對時間序列進行預測。

（三）ARIMA-LSTM預測框架

三、實證研究

（一）數據來源

本研究將河南省2010年至2020年金融機構本外幣存貸款余額共計132個月度數據作為研究對象，將2021年1-5月數據作為預測對象，編制河南省金融機構存款余額時間序列（如圖2所示）。

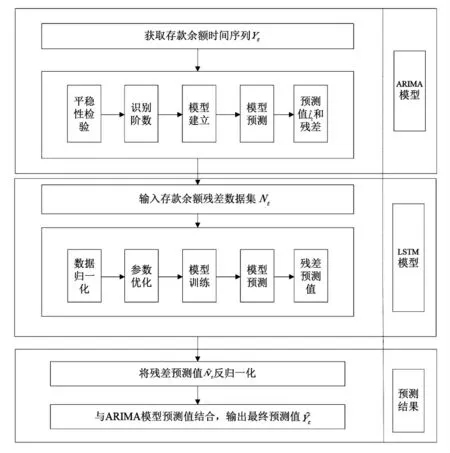
圖1 組合預測模型框架圖

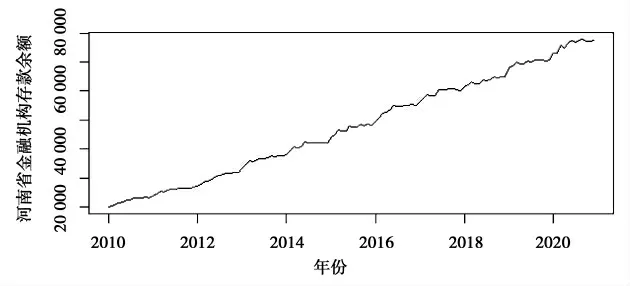
圖2 2010年至2020年河南省金融機構本外幣存貸款余額 單位：億元

（二）ARIMA模型建立及預測

建立ARIMA模型首先需要確定序列是否平穩，根據存款余額時間序列圖可初步看出，序列具有明顯的增長趨勢，并非平穩序列。利用R軟件對存款余額原始序列進行ADF檢驗（檢驗結果如表1所示），同樣顯示出存款余額時間序列不平穩。

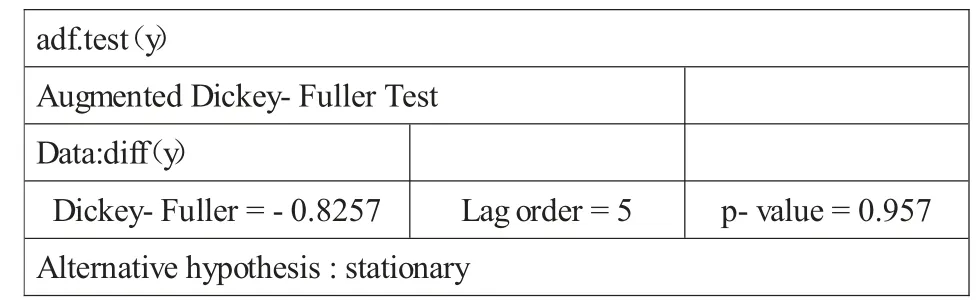
表1 原始序列ADF檢驗表

對原始序列進行一階差分來消除非平穩性。一階差分后的相關內涵如圖3上部分所示，從自相關函數圖中可以看出，延遲12階的自相關系數明顯超出兩倍標準差范圍。這說明，進行差分后的序列雖然消除了趨勢項，但仍存在著季節效應。通過12步差分運算消除季節性。存款余額季節差分圖3下部分所示，k=12時，自相關系數落入置信區間，說明季節性基本消除。

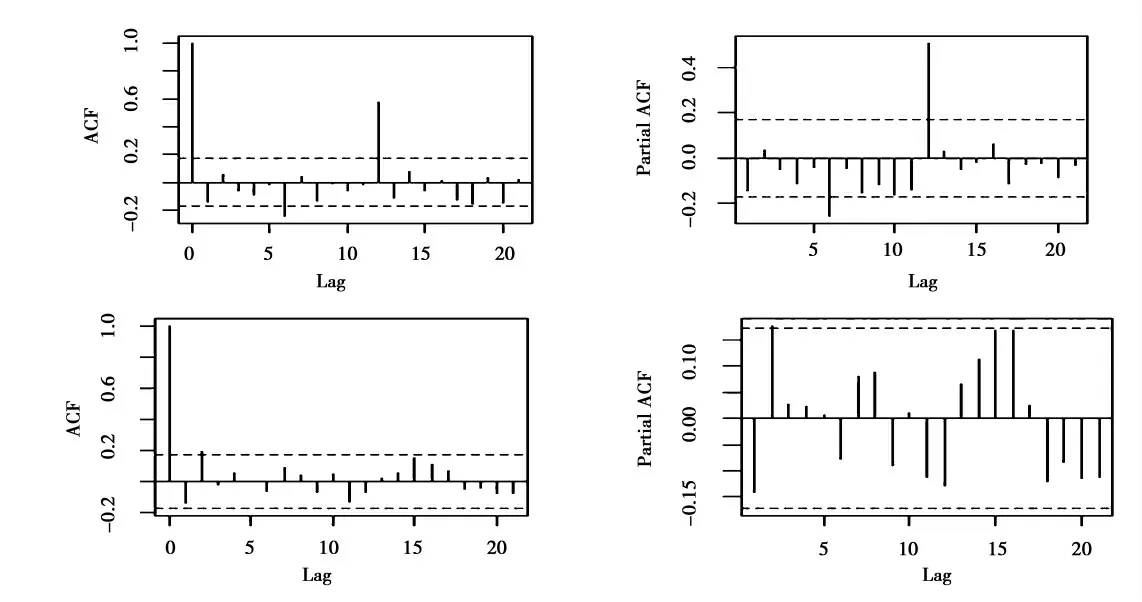
圖3 存款余額時間序列差分圖

同時，序列也通過了單位根檢驗（Dickey-Fuller=-4.8726，p-value=0.01），序列平穩后，進入模型識別階段。經過研究的檢驗和R軟件auto.arima函數的識別，確定ARIMA（0，1，0）（0，1，1）12模型。然后，利用Box.test函數檢驗擬合的時序模型的殘差是否存在自相關性。結果如表2所示，p值大于0.05，說明殘差序列不存在相關性，選定的模型能夠很好地捕獲原序列中的相關關系。最后，輸出模型預測值和殘差，以便LSTM模型的計算。

表2 殘差白噪聲檢驗

（三）LSTM模型及預測結果

研究的實驗環境基于Python3.6平臺，采用Keras深度學習框架搭建LSTM網絡。為找出模型返回最高精度的最優參數配置，設置全部數據的80%為訓練集，20%為測試集。此外，為減少數據不同量綱帶來的影響，通過對sklearn包中MinMaxScaler函數的調用，在數據處理前將數據進行歸一化處理。預測完畢再對預測值進行反歸一化，便可得到真實預測值。為了驗證模型的泛化能力，采用均方根誤差（RMSE）、平均絕對誤差（MAE）指標評估預測模型的性能。

劃分數據集后設置模型超參數，LSTM神經網絡的優勢在于可以靈活調節模型參數。超參數中的層中神經元數和層數尤為重要。按照以往的研究，將神經元個數設置為10、20和50。設置訓練批次為64，迭代次數為32，并使用過去5組數據作為特征，后一組數據作為標簽對存款余額殘差序列進行訓練。通過表3可知，當單元數都為50時，模型的效果最好。當繼續增加單元數時，模型的損失值變大，效果并不如50的單元數，所以將50設置為最適宜的單元數。

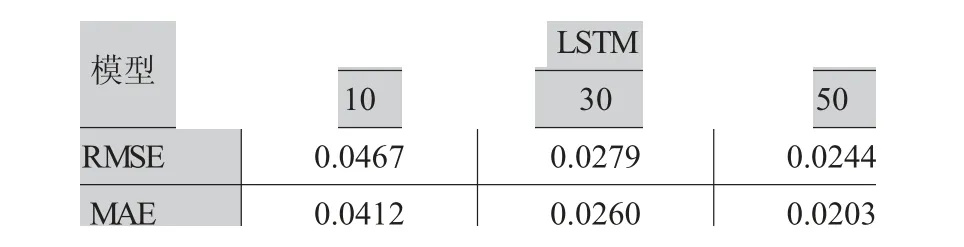
表3 不同單元數對比分析

模型的層數反應網絡的深度，研究在進行模型最佳層數分析時，在每一層LSTM層后加上Dropout層，以便神經網絡在訓練過程中舍棄某部分不需要的神經元，提高訓練速度減少過擬合。將每層的單元數均設置為50對層數進行測試。不同層數實證結果如表4，通過對比兩個評價指標發現，兩層的模型效果最佳。原因可能在于一層的模型無法抓取數據背后的信息，三層的模型過于復雜導致冗余現象。模型訓練完畢后，輸出預測的殘差值。

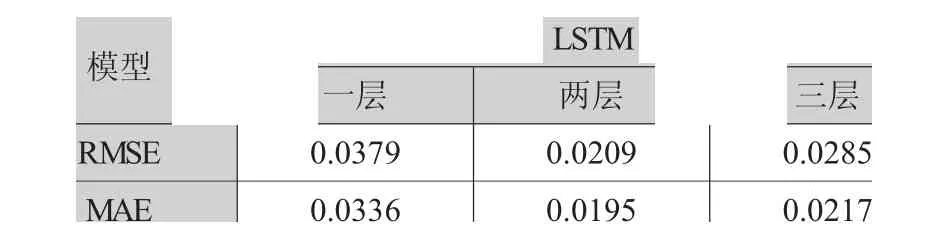
表4 不同層數對比分析

（四）ARIMA-LSTM組合模型

經過實證研究，選定ARIMA（0，1，0）（0，1，1）模型的預測值作為最終預測的存款余額線性部分，選定兩層各50單元數的LSTM模型的預測值作為最終預測的存款余額的非線性部分。則ARIMA模型和ARIMA-LSTM模型擬合值如下所示，其中ARIMA模型擬合值的相對誤差的平均值為0.0039，而ARIMA-LSTM組合模型擬合值的相對誤差0.0027。組合模型的誤差降低了28.21%，說明相對于單一的ARIMA模型，組合模型對預測精度的提升具有一定的幫助。

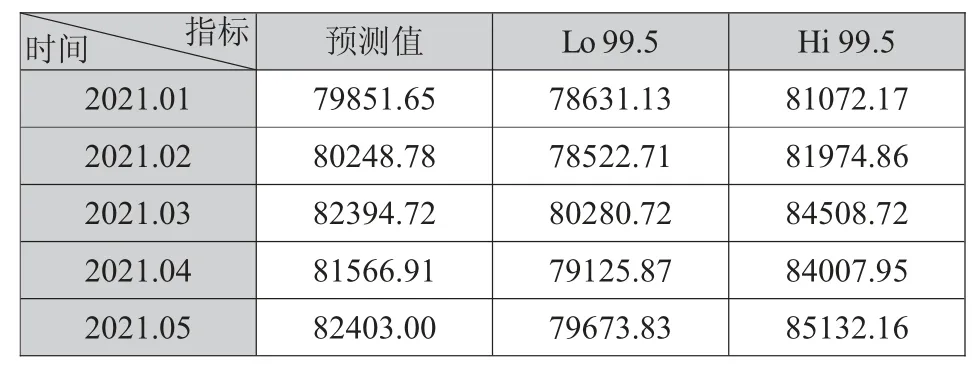
表6 ARIMA模型預測值

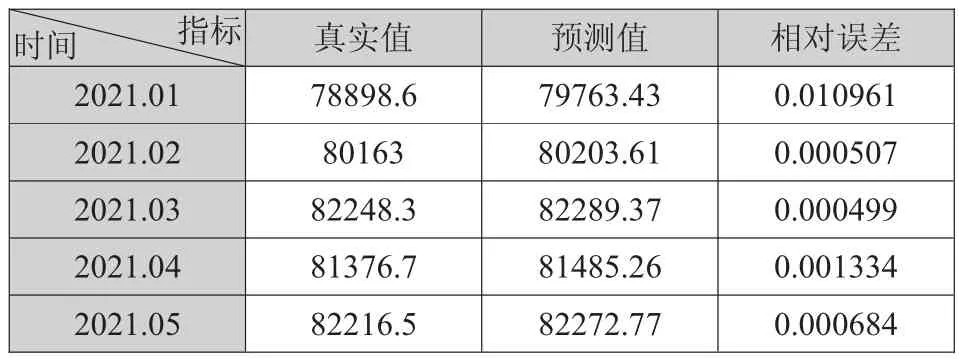
表6 ARIMA-LSTM組合模型預測值

四、結語

金融是現代經濟的核心，是實體經濟的血脈。金融機構存款余額的穩定增長顯示出金融機構聚集資金的能力增強。依據金融時間序列分析的原理和方法判斷數據的趨勢變化研究具有一定的現實意義。就金融機構存款余額的預測來說，ARIMA和LSTM組合模型能夠綜合兩者在線性和非線性方面的優勢，充分利用自身強大的數據特征提取能力和學習能力，避免單一模型的不足。

總之，本研究主要分析了ARIMA-LSTM組合模型在金融機構存貸款預測中的應用。首先，介紹了模型的原理；其次，結合ARIMA的線性預測優勢和LSTM對非線性數據的挖掘能力，得出了季節ARIMA模型對存款余額線性趨勢，LSTM模型對存款余額非線性趨勢有較好的預測效果。最后，建立了用于預測存款余額的組合模型。從實證結果來看，ARIMA-LSTM預測的預測誤差均小于單一模型，說明組合模型在存款余額預測中有著良好的適用性。