一種碳化硅器件三電平電路的損耗計(jì)算方法
呂志通, 李雪, 遲頌
(1.省部共建電工裝備可靠性與智能化國家重點(diǎn)實(shí)驗(yàn)室(河北工業(yè)大學(xué)),天津 300130;2.河北省電磁場(chǎng)與電器可靠性重點(diǎn)實(shí)驗(yàn)室(河北工業(yè)大學(xué)),天津 300130)
0 引 言
隨著電力電子技術(shù)的發(fā)展和逆變器在工業(yè)領(lǐng)域的大量應(yīng)用,基于Si器件的逆變器已漸漸地?zé)o法滿足如今工業(yè)上對(duì)高效率、高功率密度的要求,因此,SiC 器件應(yīng)運(yùn)而生。SiC器件相比于Si器件具有耐高壓、耐高溫、損耗低、工作頻率高等優(yōu)勢(shì),具有廣闊的發(fā)展?jié)摿1]。
20世紀(jì)80年代三電平逆變器首次被A.Nabae等人提出后[2],只有二極管箝位式三電平逆變器在中壓大功率場(chǎng)合得到了廣泛應(yīng)用。這種逆變器是通過箝位二極管以及串聯(lián)直流電容器來產(chǎn)生三電平交流電壓,且由于其斬波頻率高,諧波小,有利于優(yōu)化濾波器的設(shè)計(jì),所以能更好地應(yīng)用到高速電機(jī)的驅(qū)動(dòng)中。而對(duì)于逆變器而言,無論采用Si器件還是SiC器件,損耗一直是影響其性能的重要因素,因此分析逆變器的損耗變得很有必要。文獻(xiàn)[3-5]基于開關(guān)器件的物理模型提出了損耗的計(jì)算方法,由于其復(fù)雜的物理開關(guān)過程,導(dǎo)致計(jì)算量大,大量消耗CPU資源。文獻(xiàn)[6-8]均基于IGBT器件數(shù)據(jù)手冊(cè)提供的初始飽和電壓來計(jì)算損耗,對(duì)未提供該項(xiàng)參數(shù)的部分SiC器件不適用。僅基于開關(guān)器件理想的開通關(guān)斷波形來計(jì)算開關(guān)損耗,脫離實(shí)際工況,會(huì)造成較大誤差。因此文章基于平均值法來建立導(dǎo)通損耗的數(shù)學(xué)模型,簡化計(jì)算過程;在開關(guān)器件數(shù)據(jù)手冊(cè)基礎(chǔ)上建立開關(guān)損耗模型,因?yàn)閿?shù)據(jù)手冊(cè)中雖然沒有提供初始飽和壓降,但提供了器件具體的開關(guān)損耗數(shù)據(jù),利用曲線擬合的方式估算開關(guān)損耗更貼近器件的實(shí)際工況。
為了選擇一個(gè)損耗較低的三電平電路拓?fù)溆糜诟咚匐姍C(jī)的驅(qū)動(dòng),同時(shí)為了驗(yàn)證方法的正確性,對(duì)基于SiC器件的單相三電平I型電路和T型電路的損耗進(jìn)行計(jì)算分析,并利用PLECS仿真軟件進(jìn)行仿真實(shí)驗(yàn)。兩種電路如圖1和圖2所示。
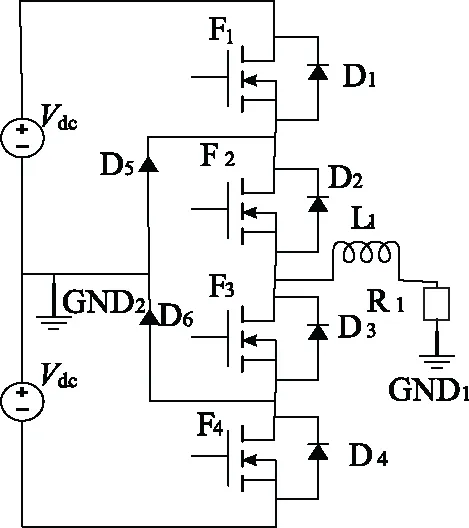
圖1 I型電路
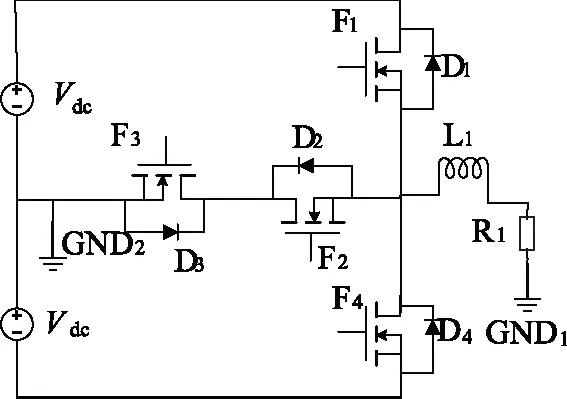
圖2 T型電路
1 數(shù)學(xué)模型與計(jì)算
研究的單相三電平I型拓?fù)浜蚑型拓?fù)洳捎玫氖荢PWM調(diào)制方式,如圖3所示,開關(guān)器件采用CAS120M12BM2(1.2 kV/193 A),負(fù)載采用阻感負(fù)載。直流側(cè)用直流電源代替。

圖3 SPWM調(diào)制開關(guān)波形
兩種拓?fù)潆娐返倪\(yùn)行過程分析如下:圖1中,對(duì)于I型拓?fù)潆娐罚?dāng)開關(guān)器件F1和F3交替導(dǎo)通的時(shí)候,F(xiàn)2一直處于高電平,忽略死區(qū)時(shí)間,當(dāng)F1導(dǎo)通時(shí),電流經(jīng)F1和F2流通,當(dāng)F1關(guān)斷時(shí),無論電流是正還是負(fù),電流都會(huì)經(jīng)一個(gè)MOSFET和一個(gè)二極管續(xù)流;當(dāng)F2和F4交替導(dǎo)通時(shí),F(xiàn)3一直高電平,當(dāng)F4導(dǎo)通時(shí),電流經(jīng)F3和F4導(dǎo)通,當(dāng)F4關(guān)斷時(shí),同樣無論電流是正還是負(fù),電流都會(huì)經(jīng)一個(gè)MOSFET和一個(gè)二極管續(xù)流。圖2中對(duì)于T型拓?fù)潆娐罚刂品绞揭粯樱煌氖呛雎运绤^(qū)時(shí)間后,F(xiàn)1導(dǎo)通,電流經(jīng)F1導(dǎo)通,F(xiàn)1關(guān)斷后,由F2和F3續(xù)流;F4導(dǎo)通,電流經(jīng)F4流通,F(xiàn)4關(guān)斷后,由F2和F3續(xù)流。
1.1 導(dǎo)通損耗
由于開關(guān)頻率fs遠(yuǎn)大于調(diào)制波頻率f0,在一個(gè)開關(guān)周期內(nèi)電流變化不大,可以按照恒定電流計(jì)算,即將一個(gè)連續(xù)的輸出電流可以用下式離散化[9]:
io=IPsin(θn-φ)
(1)
(2)
式中IP是輸出電流峰值;N=fs/f0,φ是相角。
如圖4所示,占空比采用規(guī)則采樣法進(jìn)行估算,調(diào)制度為m,取m=1,調(diào)制波幅值為Vs,三角波幅值為Vt。

圖4 占空比估算
由于調(diào)制波(Sine Wave2)高于三角波的那部分電流數(shù)值變化很小,因此可以近似認(rèn)為該段曲線為平行于水平軸的一段直線,占空比等于該段直線的長度與開關(guān)周期的比值,由三角形相似可知進(jìn)一步等于該段直線中點(diǎn)處的電流值與三角波幅值之比,而在整個(gè)調(diào)制波周期內(nèi),每段近似直線的中點(diǎn)之間的間隔為一個(gè)開關(guān)周期,因此調(diào)制波也可以用式(1)和式(2)的方法進(jìn)行離散,調(diào)制波初始相位為0,則調(diào)制波的離散式以及占空比的計(jì)算式如下:
vr=Vsinθn
(3)
(4)
D′=1-D=1-msinθn
(5)
對(duì)于I型電路,忽略死區(qū)時(shí)間,F(xiàn)1和F3運(yùn)行的半個(gè)周期內(nèi)過程可以分為兩類:一是F1開通時(shí)會(huì)有兩個(gè)MOSFET同時(shí)導(dǎo)通,占空比為D;二是F1關(guān)斷時(shí)會(huì)有一個(gè)MOSFET和一個(gè)二極管導(dǎo)通,占空比為D′。則半個(gè)周期內(nèi),第一類的導(dǎo)通損耗,即N/2個(gè)開關(guān)周期內(nèi)的導(dǎo)通損耗之和為:
(6)
則半個(gè)周期內(nèi),第二類情況的導(dǎo)通損耗之和為:
(7)
式中IP,i為I型電路輸出電流峰值;RF為MOSFET導(dǎo)通電阻;RD為二極管導(dǎo)通電阻。查詢器件數(shù)據(jù)手冊(cè)中二極管導(dǎo)通電流和導(dǎo)通壓降曲線關(guān)系可知,二極管導(dǎo)通電阻受溫度影響很小,約為13 mΩ。但是MOSFET導(dǎo)通電阻受溫度影響較大,其值為:
RF=R0+KΔT
ΔT=PlossRthJCM
式中R0為結(jié)溫25 ℃時(shí)的導(dǎo)通電阻,為13.2 mΩ,K為溫度調(diào)整系數(shù),由數(shù)據(jù)手冊(cè)所給結(jié)溫和導(dǎo)通電阻的關(guān)系確定;ΔT為溫升;RthJCM為熱阻,由數(shù)據(jù)手冊(cè)給出;Ploss為功率損耗。又因?yàn)镕2和F4的運(yùn)行方式與F1和F3運(yùn)行方式一樣,所以F2和F4運(yùn)行的半個(gè)周期內(nèi)的兩類情況產(chǎn)生的導(dǎo)通損耗同式(6)和式(7),在一個(gè)周期內(nèi),總的導(dǎo)通損耗為:
(8)
對(duì)于T型電路,忽略死區(qū)時(shí)間,F(xiàn)1和F3運(yùn)行的半個(gè)周期內(nèi)運(yùn)行過程也可以分為兩類:一是F1開通時(shí),只有一個(gè)MOSFET導(dǎo)通,占空比為D;二是F1關(guān)斷時(shí),會(huì)有兩個(gè)MOSFET導(dǎo)通,占空比為D′。則半個(gè)周期內(nèi),第一類的導(dǎo)通損耗,即N/2個(gè)開關(guān)周期內(nèi)的導(dǎo)通損耗之和為:
(9)
則半個(gè)周期內(nèi),第二類情況的導(dǎo)通損耗之和為:
(10)
式中IP,t為T型電路的輸出電流峰值。又因?yàn)镕2、F4工作的半個(gè)周期內(nèi)產(chǎn)生的導(dǎo)通損耗與F1、F3半個(gè)周期內(nèi)產(chǎn)生的導(dǎo)通損耗一樣,則在一個(gè)周期內(nèi)總的導(dǎo)通損耗為:
(11)
1.2 開關(guān)損耗
器件的開關(guān)損耗在數(shù)據(jù)手冊(cè)中都會(huì)給出相應(yīng)曲線,數(shù)據(jù)均為廠家在器件實(shí)際運(yùn)行時(shí)所測(cè)得的數(shù)據(jù),與物理模型的計(jì)算相比更接近實(shí)際工況。采用的是SiC MOSFET和并聯(lián)二極管的封裝模塊,查看其數(shù)據(jù)手冊(cè)可知二極管的反向恢復(fù)電流為0,因此二極管只有導(dǎo)通損耗。
對(duì)于 MOSFET的開關(guān)損耗曲線,由于斜率變化很小,如圖5所示,采用直線與損耗曲線進(jìn)行擬合,電流在160 A以下時(shí)貼合度比較高,高于160 A時(shí)二者的偏差變大。
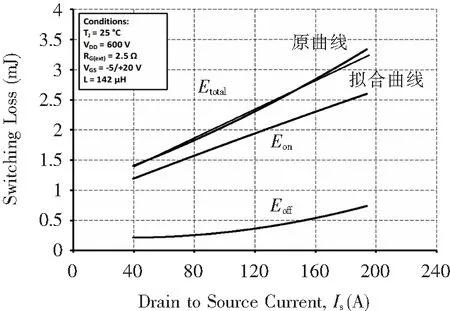
圖5 開關(guān)損耗曲線
然而所用器件在最高結(jié)溫150 ℃時(shí)電流最大值為193 A,正常工況下逆變器會(huì)工作在150 ℃以下,且必須留有一定裕量,160 A以下足以滿足大多數(shù)工況,且本文仿真實(shí)驗(yàn)負(fù)載電流均在160 A以下。因此可以采用直線擬合的方法來近似估算開關(guān)運(yùn)行時(shí)的開關(guān)損耗。但是數(shù)據(jù)手冊(cè)中只給出了基礎(chǔ)電壓下的開關(guān)損耗曲線,因此其他電壓下的開關(guān)損耗采用式(12)進(jìn)行估算[10]:
(12)

(13)
選取器件開關(guān)損耗擬合直線上的兩點(diǎn)(40,1.417)和(80,1.833),代入式(13)可得:k=0.0104,b=1.001。
電路運(yùn)行時(shí),由控制方式可知,不管I型電路還是T型電路,每一對(duì)開關(guān)器件都是運(yùn)行半個(gè)周期,對(duì)于一個(gè)開關(guān)器件來說,開關(guān)損耗為N/2個(gè)開關(guān)周期內(nèi)的開關(guān)損耗之和:
(14)
然而,I型拓?fù)潆娐分械腇1和F4適用于式(14),F(xiàn)2和F3并不適用于式(14),原因如下:當(dāng)F1和F3工作時(shí),F(xiàn)2一直處于高電平狀態(tài)。由于輸出電流和輸出電壓存在相位差,所以在F1工作的半個(gè)周期內(nèi),電流會(huì)由負(fù)值變正值。當(dāng)F1關(guān)斷且電流為正時(shí)由F2和D5續(xù)流;電流為負(fù)值時(shí)由F3和D6續(xù)流,因此F3只有在電流為負(fù)值時(shí)才存在開關(guān)損耗,并不是半個(gè)周期都存在開關(guān)損耗。又根據(jù)式(13)中k< (15) 同理當(dāng)F2和F4工作時(shí),F(xiàn)3一直處于高電平狀態(tài),F(xiàn)4關(guān)斷后且電流為負(fù)值時(shí),由F3和D6續(xù)流,當(dāng)電流為正時(shí)由F2和D5續(xù)流,此時(shí)F2才會(huì)產(chǎn)生開關(guān)損耗,且與F3開關(guān)損耗一樣。綜上所述,在一個(gè)電流周期內(nèi),I型電路4個(gè)開關(guān)器件的開關(guān)總損耗為: (16) 對(duì)于T型電路而言,由于不存在箝位二極管,因此不管電流為正值還是負(fù)值,當(dāng)忽略死區(qū)時(shí)間時(shí),F(xiàn)1和F4關(guān)斷后一直由F2和F3續(xù)流,因此4個(gè)開關(guān)器件在自己工作的半個(gè)周期內(nèi)均存在開關(guān)損耗,則一個(gè)電流周期內(nèi)T型電路4個(gè)開關(guān)器件的開關(guān)總損耗為: (17) 這里IP,i和IP,t根據(jù)參考文獻(xiàn)[11]可得: (18) (19) 令I(lǐng)型拓?fù)潆娐泛蚑型拓?fù)潆娐吩谝粋€(gè)基波周期內(nèi)的總損耗相等: (20) 經(jīng)過數(shù)學(xué)方式化簡得: (21) r,n,t定義如下: r=1.135+0.107RF; 由式(21)可以看出,令I(lǐng)型拓?fù)浜蚑型拓?fù)鋼p耗相等的開關(guān)頻率(暫且稱之為交點(diǎn)頻率)隨直流母線電壓和輸出功率因數(shù)的增大而增大,隨負(fù)載電阻的增大而減小。 為了驗(yàn)證理論公式的正確性,使用PLECS仿真軟件[12]搭建了單相三電平I型拓?fù)浜蚑型拓?fù)潆娐贩抡婺P汀2⒏鶕?jù)器件的數(shù)據(jù)手冊(cè),將開關(guān)器件的有關(guān)參數(shù)輸入到PLECS軟件中,建立了CAS120M12BM2器件的熱模型。 PLECS輸出結(jié)果如圖6~圖8所示,每張圖由三組共6條曲線組成。每組曲線開關(guān)頻率一樣,實(shí)線代表I型拓?fù)鋼p耗,虛線代表T型拓?fù)鋼p耗。這三組曲線對(duì)應(yīng)的開關(guān)頻率分別為小于交點(diǎn)頻率,等于交點(diǎn)頻率和大于交點(diǎn)頻率。表1~表3是逆變電路損耗的計(jì)算與仿真結(jié)果。 圖6 Vdc=300 V,R=2 Ω時(shí)損耗曲線 圖7 cosφ=0.85,R=2 Ω時(shí)損耗曲線 圖8 Vdc=300 V,cosφ=0.85時(shí)損耗曲線 表1 Vdc=300 V,R=2 Ω時(shí)損耗 表2 cosφ=0.85,R=2 Ω時(shí)損耗 表3 Vdc=300 V,cosφ=0.85時(shí)損耗 分析表1可知,當(dāng)開關(guān)頻率低于交點(diǎn)頻率時(shí)T型損耗較低;當(dāng)開關(guān)頻率高于交點(diǎn)頻率時(shí)I型損耗較低,這與圖6所示仿真結(jié)果一致。同理,對(duì)比分析圖7和表2,圖8和表3可知,無論直流母線電壓,負(fù)載電阻和功率因數(shù)怎么變化,當(dāng)開關(guān)頻率低于交點(diǎn)頻率時(shí),T型損耗(虛線)較低;當(dāng)開關(guān)頻率高于交點(diǎn)頻率時(shí)I型損耗(實(shí)線)較低。 接下來基于仿真結(jié)果圖,對(duì)交點(diǎn)頻率與直流母線電壓、輸出功率因數(shù)以及負(fù)載電阻的關(guān)系做進(jìn)一步分析,如圖6的3個(gè)分圖所示,當(dāng)直流母線電壓和負(fù)載電阻保持不變,功率因數(shù)由0.6增大到0.85時(shí),交點(diǎn)頻率由20 kHz增大到了31 kHz;如圖7的3個(gè)分圖所示,當(dāng)功率因數(shù)和負(fù)載電阻保持不變,直流母線電壓由300 V增大到450 V時(shí),交點(diǎn)頻率由31 kHz增大到了42 kHz;如圖8的3個(gè)分圖所示,當(dāng)直流母線電壓和功率因數(shù)保持不變,且負(fù)載電阻由2 Ω增大到4 Ω時(shí),交點(diǎn)頻率由31 kHz減少到了9 kHz。該分析結(jié)果與式(21)所反映出來的趨勢(shì)一致,將各項(xiàng)參數(shù)代入式(21)計(jì)算不同條件下的交點(diǎn)頻率,仿真結(jié)果和計(jì)算結(jié)果的對(duì)比如表4所示,計(jì)算結(jié)果反映出了與仿真結(jié)果相同的變化趨勢(shì)。 表4 仿真結(jié)果與計(jì)算結(jié)果對(duì)比 所提方法的計(jì)算結(jié)果和仿真結(jié)果存在一定誤差,主要由以下幾個(gè)原因造成: (1)為了估算不同結(jié)溫下的器件導(dǎo)通電阻,將導(dǎo)通電流160 A以下曲線近似為直線,并引入了溫度調(diào)整系數(shù)。而實(shí)際工況下,導(dǎo)通電阻隨溫度的變化并非嚴(yán)格呈正比例變化,因此導(dǎo)致了誤差; (2)由于器件手冊(cè)只給出了具體直流母線電壓下的開關(guān)損耗,而不同直流母線電壓條件下的開關(guān)損耗只能基于數(shù)據(jù)手冊(cè)采用比例法估算,且直線擬合的方式也會(huì)導(dǎo)致較小誤差; (3)將負(fù)載電流進(jìn)行離散化,且每個(gè)開關(guān)周期內(nèi)近似認(rèn)為電流恒定,導(dǎo)致了一定誤差; (4)占空比的近似計(jì)算方法也導(dǎo)致了較小的誤差。 但是,由表1~表4所示的計(jì)算與仿真結(jié)果的比較可知,誤差均在5%以內(nèi),說明該計(jì)算方法具有一定可靠性。 基于平均值法和器件數(shù)據(jù)手冊(cè)中的損耗參數(shù)提出了一種損耗計(jì)算方法,并利用此方法對(duì)單相三電平I型和T型電路進(jìn)行了損耗分析,最后利用PLECS電力電子仿真軟件進(jìn)行了實(shí)驗(yàn)驗(yàn)證,結(jié)果表明該方法的計(jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)誤差在5%以內(nèi),證明了方法的可行性。該方法既有必要的精度,又簡化了計(jì)算過程,并對(duì)高速電機(jī)驅(qū)動(dòng)系統(tǒng)的選型具有一定的指導(dǎo)意義。1.3 計(jì)算損耗相等的開關(guān)頻率
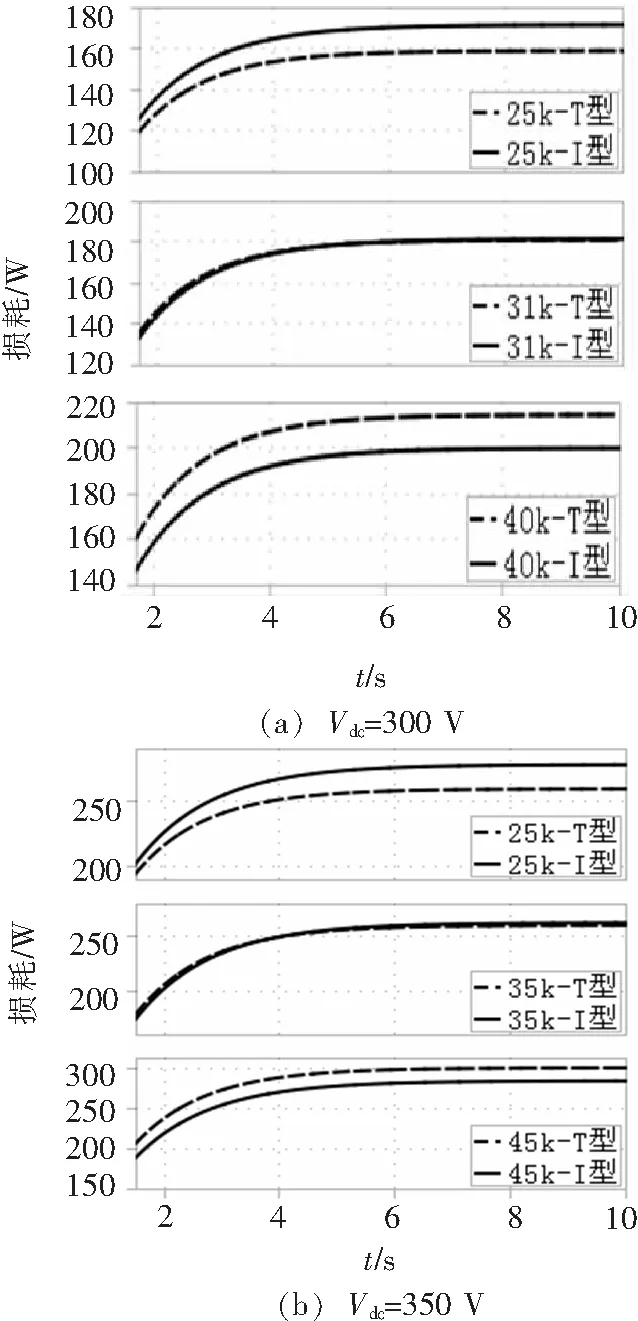
2 仿真實(shí)驗(yàn)驗(yàn)證

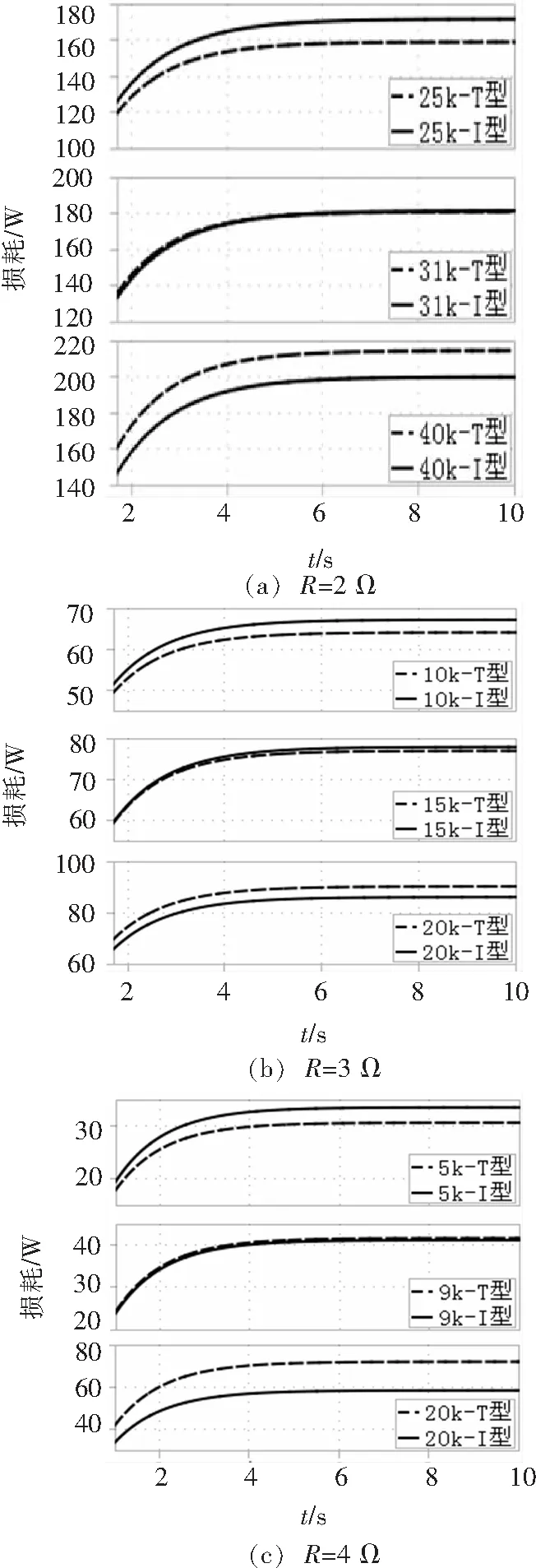
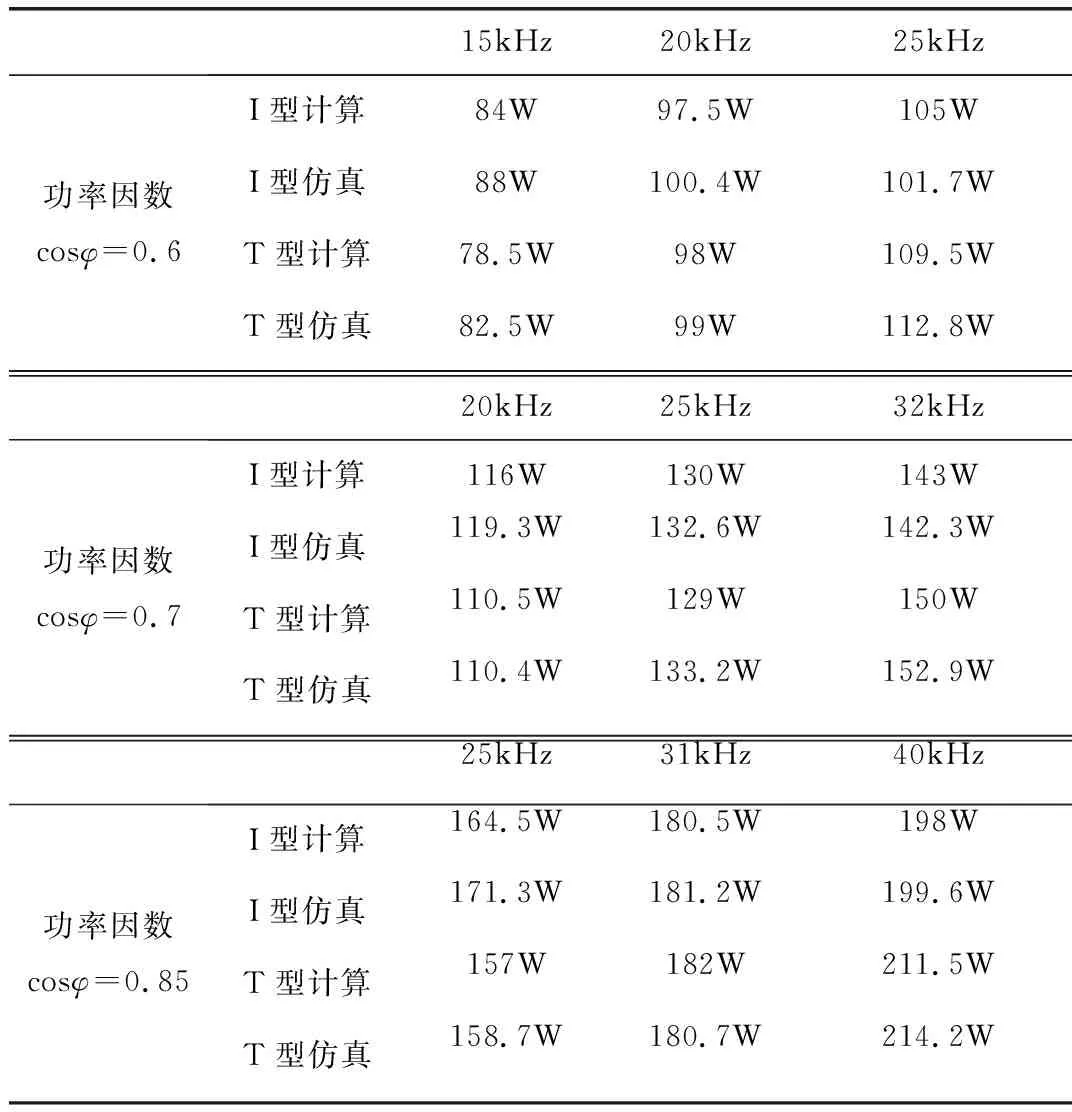


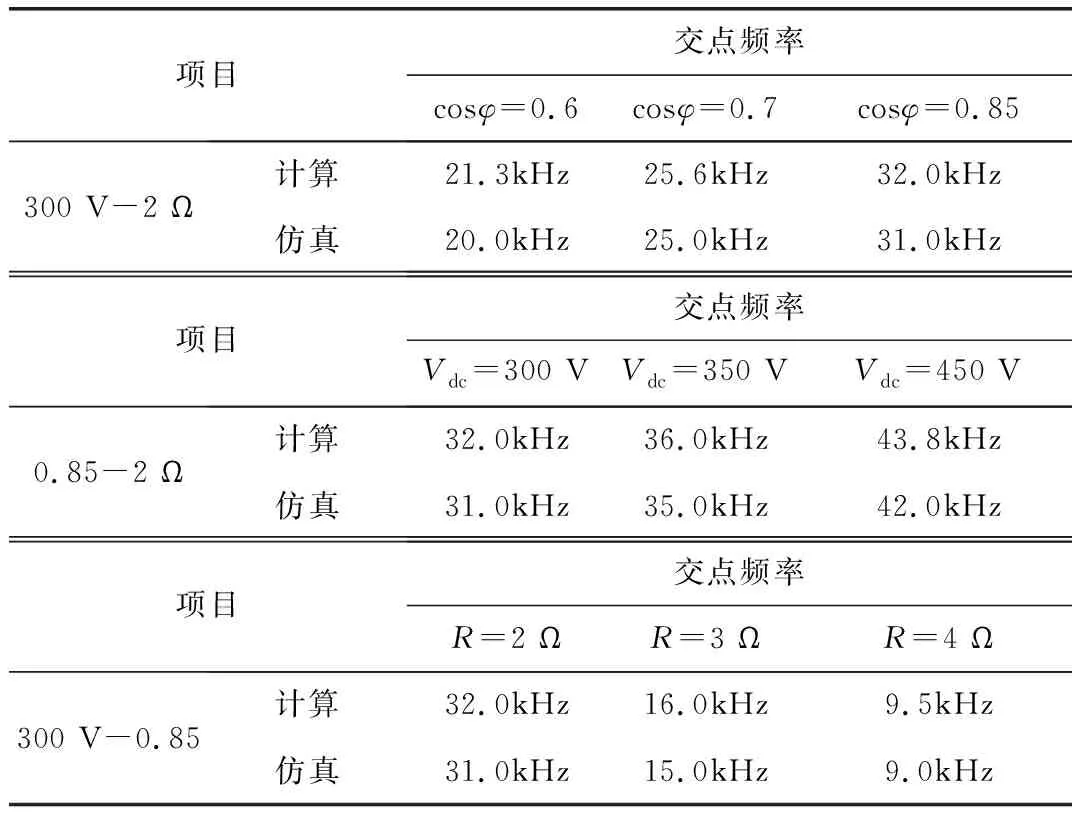
3 誤差分析
4 結(jié)束語

