軸對稱內錐流動中馬赫盤的形成與演化

姬雋澤，李祝飛，*，司東現，張 濤，施崇廣，尤延鋮，楊基明

(1. 中國科學技術大學，合肥 230027；2. 廈門大學，廈門 361102)

0 引 言

近年來，內轉式進氣道[1-4]憑借諸多性能優勢，在吸氣式高超聲速飛行器的研發中展示了誘人的潛力。然而，由于內轉式進氣道普遍是基于軸對稱內收縮基準流場進行設計的，其內部流動存在匯聚效應[5-8]，與二元進氣道相比更為復雜，甚至存在本質性差異。一般而言，二元進氣道內部的激波相互作用通常表現為平面激波的入射和反射[9-10]，并存在規則反射和馬赫反射兩種反射類型[11]。然而，在軸對稱內收縮流場中[12-14]，內錐形的入射激波會持續向中心匯聚增強，最終必然在軸線上發生馬赫反射[15-16]。在工程實際中，馬赫反射區域具有強壓縮損失和弱抗反壓能力等特性[12,17]，會給進氣道性能帶來嚴重的負面影響，因此應極力避免。

長久以來，通過在軸對稱內收縮基準流場中設置中心體將軸線區域掩蓋，進而規避馬赫反射的措施[12,18]，在內轉式進氣道設計中被廣泛采納。實際上，這種措施在給進氣道設計帶來便利的同時，并未促進流動機理認識的提升，甚至制約了設計理論及方法的持續創新。因此，隨著對內轉式進氣道流場品質的要求日益嚴苛，越來越多的研究者開始重視軸對稱內錐流動中的激波反射問題，并嘗試探索理論求解方法。譚廉華等[19-20]從軸對稱內錐形激波和馬赫盤入手，較早地給出了確定它們形狀的理論關系式。近年來，彎曲激波理論[21-25]（Curved shock theory，簡稱CST）逐步得到廣泛應用。該理論可以在已知內錐流動中入射激波和馬赫盤形狀的前提下，計算出反射激波的局部形狀以及波后流動的高階參數。將上述兩種理論相結合，似乎可以逐次確定軸對稱內錐流動中原本難以解析的激波形狀，給理論求解軸對稱內錐形激波反射問題帶來了新的曙光。然而，應用這兩種理論均涉及到馬赫盤位置這一關鍵參數。由于目前缺乏對軸對稱內錐流場中馬赫盤形成機理及馬赫盤下游流動的深入認識，從理論上確定馬赫盤位置的研究仍鮮見報道。

根據平面激波反射理論可知[11]，當入射激波的角度β大于von Neumann準則規定的激波角βN時，有可能發生馬赫反射。對于平面激波的馬赫反射結構，入射激波、反射激波和馬赫桿的波后氣流偏轉角關系（即三激波理論）是唯一確定的。由于平面激波的β保持恒定，三激波理論可以在平面激波的任意位置成立。于是，馬赫桿的形成位置僅由其下游流動決定[11,26]。

與平面激波相比，軸對稱內錐形激波隨著向中心匯聚，自身的激波角β具有持續增大的特點，使得影響馬赫盤位置的因素變得更為復雜。在軸對稱內錐形激波的入射過程中，當β尚未增大至βN時，不能形成馬赫反射結構。換言之，軸對稱內錐形入射激波自身的匯聚增強過程會限制馬赫盤可能存在的空間范圍。進一步地，雖然三激波理論在β超出βN之后成立，但是三激波理論中的反射激波后的氣流偏轉角不是唯一確定的，而是與當地入射激波的β緊密相關。由此可見，在確定軸對稱內錐形激波反射流場中馬赫盤位置時，入射激波自身的強度變化需要予以考慮。然而，關于馬赫盤位置與激波匯聚增強過程之間的關系，目前鮮見報道。

此外，與平面激波馬赫反射類似的是，在軸對稱內錐形激波反射流場中馬赫盤下游流動也會影響馬赫盤位置。Gounko[27]通過改變軸對稱內錐模型的壁面長度，獲得了不同的馬赫盤下游流動條件及馬赫盤位置，但并沒有闡明馬赫盤下游流動對其形成位置的影響機理。在下游流動影響下，馬赫盤的形成及演化規律仍有待系統地研究。

綜上所述，本文綜合考慮軸對稱內錐形激波匯聚過程及馬赫盤下游流動兩方面的因素，采用無黏數值模擬，考察內收縮直錐的壁面前緣角度和壁面長度對馬赫盤位置的影響，揭示形成馬赫盤的內在機制及其演化規律，以期豐富對軸對稱基準流場的認識并支撐內轉式進氣道設計潛力的挖掘。

1 模型和數值方法

如圖1所示，利用軸對稱內收縮直錐生成內錐形激波，采用原點位于模型入口圓心處的軸對稱坐標系，其中x為軸線方向，r為半徑方向。該模型的壁面前緣半徑R= 100 mm，前緣壓縮角度為θw，無量綱的壁面長度為w/R。參考內轉式進氣道基準流場設計參數[28]，選取的壁面前緣角度范圍為θw= 8°～15°，通過改變θw得到具有不同初始強度的激波，繼而調節內錐形激波的匯聚增強過程。在每個給定的θw工況下，通過選取不同的壁面長度w/R來改變壁面尾緣膨脹波的位置，進而產生不同的馬赫盤下游流動條件。當壁面太短時，尾緣膨脹波靠近上游，會對入射的內錐形激波產生干擾；而壁面太長時，內收縮比過大，超聲速流場難以建立。因此，w/R取值約束在一定范圍內[11,26]。表1列出了本文所有工況中θw和w/R的取值。表1中，w/R最大值和最小值為w/R可取的極限值，在本文中不作為主要討論的工況。

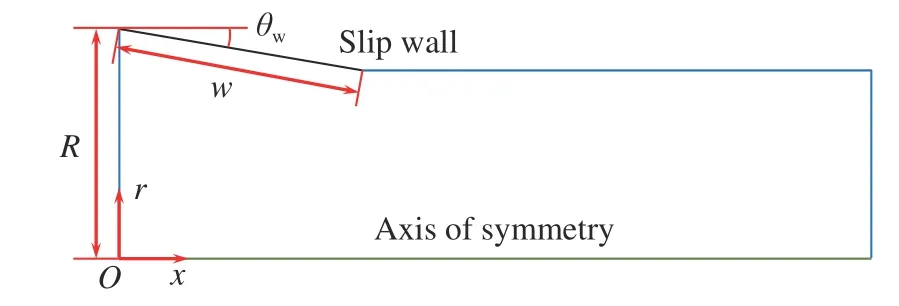
圖1 模型及計算域Fig. 1 Model and computational domain

表1 數值計算工況Table 1 Calculation conditions

鑒于本文主要關注內收縮直錐軸線附近的波系結構，黏性和邊界層效應對遠離壁面的主要激波及其反射結構的影響可以忽略[5,24]，因而通過求解理想氣體（比熱比γ= 1.4）的歐拉方程，對軸對稱內收縮直錐流場進行CFD （Computational Fluid Dynamics）定常模擬。空間差分采用總變差減小（TVD）的迎風格式[29]，數值通量采用HLLC（Harten-Lax-van Leer-contact）近似黎曼求解器[30-31]計算。在所有計算工況下，均采用結構化網格將計算域離散。計算域如圖1所示，除壁面和軸線邊界外，其他邊界均采用無反射的遠場條件[19,24]。遠場來流條件與文獻[6]中保持一致，馬赫數Ma∞= 6，靜壓p∞= 0.9 kPa。在計算過程中監測各方程殘差，待殘差下降4～5個數量級且波系結構穩定后，認為流場計算收斂。

為考核網格無關性，分別采用單元尺度為Δx/R≈Δr/R≈ 0.002和0.001的兩套網格進行計算，其中Δx和Δr分別為單個網格沿x和r方向的長度。將獲得的流場進行對比，發現馬赫盤位置沿x方向的變化量僅約為0.001R，兩套網格的主要波系結構幾乎重合。因此，本文所有工況的數值模擬都采用單元尺度為Δx/R≈ Δr/R≈ 0.001的網格。

為驗證本文數值模擬方法的可靠性，以θw= 10°、w/R= 1的工況為例，與文獻[6]中的實驗結果進行了對比。如圖2所示，將數值模擬得到的馬赫數等值線（紅色實線）疊加在風洞實驗[6]紋影照片上可以看出，數值模擬給出的馬赫盤位置稍靠下游，與實驗結果相距僅約為0.0008R，兩者的主要激波反射結構基本重合。這也表明本文的數值模擬結果是可靠的。

2 結果與討論

2.1 軸對稱內錐流動基本結構

鑒于w/R不影響軸線附近的激波反射類型，本節統一選取w/R= 1.5，并以θw= 10°工況為例，簡要介紹軸對稱內錐流動中的基本激波結構。

圖3（a）展示了θw= 10°、w/R= 1.5工況的流場馬赫數（Ma）云圖及等值線，圖3（b）將激波反射結構所在區域（虛線框Ⅰ）進行了局部放大顯示。結合圖3（a）和圖3（b）可以看出，壁面前緣產生的軸對稱內錐形入射激波IS在向下游發展的過程中持續地匯聚增強，尤其在接近軸線（r/R= 0）時出現較為劇烈的彎曲。最終，IS在軸線附近發生馬赫反射，匯聚過程被馬赫盤MD終結，同時在三波點T處形成反射激波RS和剪切層SL（在本文討論中不考慮SL的厚度，將其視為滑移線[11]）。壁面尾緣產生的膨脹波EW會透射過RS并入射在SL上，對SL產生干擾。圖3（c）將MD下游的局部流場（圖3（a）中虛線框Ⅱ）進行了放大顯示，可以看出，在緊鄰MD下游的區域，SL下方與軸線包裹的流管內是亞聲速氣流；隨著SL向下游延伸，流管內的氣流逐漸加速至超聲速。換言之，在SL下方與軸線包裹的流管內，會形成聲速喉道。在上、下游流動的影響下，SL的形態在聲速喉道的形成過程中，扮演著重要的角色。

在來流Ma∞= 6條件下，由平面激波反射理論可知[11]，對于氣流偏轉角同樣為θw（見表1）的平面激波而言，理論上均不存在馬赫反射。對于軸對稱內錐形激波而言，雖然其初始強度等同于氣流偏轉角為θw的平面激波（壁面前緣處的波后氣流偏轉角完全由壁面約束），但是在匯聚增強的過程中，內錐形入射激波IS會超出von Neumann準則對應的激波強度[11]（稱為von Neumann強度[32]），使得馬赫反射對應的入射激波強度條件得以滿足（見圖3）。鑒于馬赫盤位置應當在入射激波強度達到von Neumann強度之后，允許馬赫盤存在的空間范圍取決于軸對稱內錐形激波的匯聚增強過程。此外，在該空間范圍內，三波點需與馬赫盤下游的流動條件相匹配，因此馬赫盤的位置受其下游流動的影響。

為深入探究影響馬赫盤位置的機制，需要從兩個方面入手：首先，通過改變壁面前緣角度，考察激波匯聚增強過程對馬赫盤位置的影響；然后，通過改變壁面長度，進一步考察馬赫盤下游流動對馬赫盤位置的影響。

2.2 壁面前緣角度對馬赫盤位置的影響

由2.1節可知，壁面前緣角度θw決定了軸對稱內錐形入射激波的初始強度，并通過影響激波匯聚過程來限制允許馬赫盤存在的空間范圍。因此，闡明θw對內錐形激波匯聚過程的影響是十分必要的。

根據譚廉華等[19-20]提出的理論，軸對稱內錐形入射激波形狀r=r(x)可以表達為二階非線性常微分方程式（1）和式（2）：

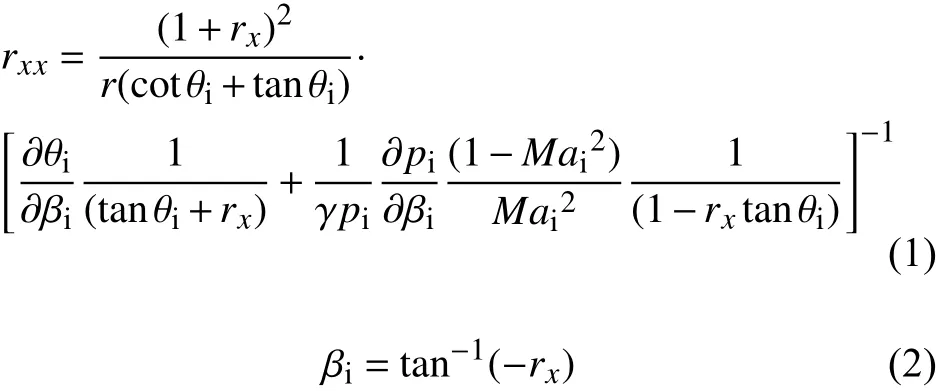
其中，rx和rxx分別表示r關于x的一階導數和二階導數，入射激波后的氣流偏轉角θi、壓力pi以及馬赫數Mai均是入射激波角βi的函數。對于本文而言，式（1）存在形如式（3）和式（4）的兩個邊界條件，

其中，壁面前緣處的激波角βw由Ma∞和θw確定。可見，θw是影響激波匯聚增強過程的重要參數。

以w/R= 1.5工況為例，采用Runge-Kutta法[33]對式（1）～式（4）進行積分，得到了不同θw下的入射激波形狀，如圖4所示。同時，在圖4中還疊加了本文數值模擬獲得的入射激波及馬赫盤形狀。對比圖4中的結果可知，在不考慮發生馬赫反射的情況下，譚廉華等[19-20]的理論能夠較為準確地給出入射激波的形狀。由于式（1）～式（4）是基于入射激波波后流線為直線這一假設[19-20]推導而來的，而實際流場中入射激波波后流線存在曲率[21]，因此，圖4中的理論和數值模擬結果存在一定的偏差。然而，這種偏差很小，式（1）～式（4）仍不失為一種描述入射激波形狀的有效理論。需要特別注意的是，式（1）～式（4）在軸線處（r/R= 0）存在奇性，在入射激波到達軸線之前，必然會發生馬赫反射并形成馬赫盤[15-16]。由于本節主要關注遠離軸線處的入射激波，不影響對內錐形激波匯聚過程的討論。

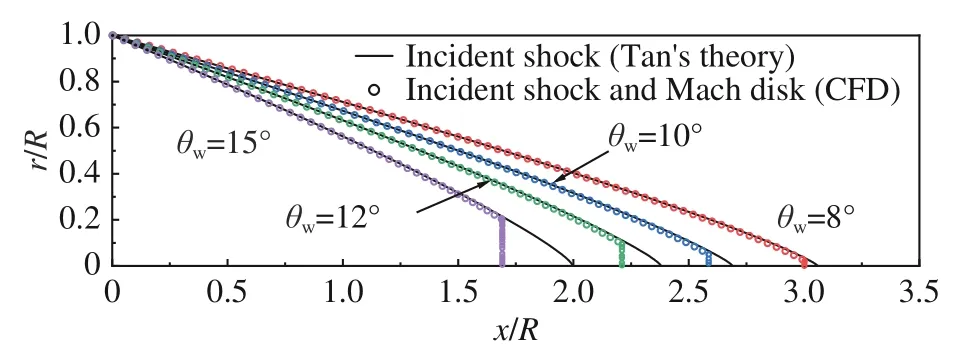
圖4 不同θw下軸對稱內錐形入射激波形狀(w/R = 1.5)Fig. 4 Shapes of axisymmetric internal conical shocks at different θw (w/R = 1.5)

鑒于式（1）～式（4）對內錐形激波匯聚增強機理的反映不夠直觀，因而結合CST對圖4中的結果進一步分析。針對任意曲面激波，CST方程[21]給出了波后當地沿流線的無量綱壓力梯度的表達式。對于均勻來流下的軸對稱內錐形入射激波而言，其波后沿流線的無量綱壓力梯度P2i可表示為式（5）[22]：

式（5）中a1和a2均為與Ma∞和βi有關的系數，Sai和Sbi分別為流平面（激波當地來流和波后氣流偏轉方向共同決定的平面）和法平面（與流平面內激波當地切向垂直的平面）內的激波曲率[22]。在壁面前緣處（x/R= 0），可以將式（5）化簡為式（6）[8]：

式（6）中系數c與初始激波強度正相關，Sci為激波的初始橫向曲率。由于在壁面前緣處R是確定的（Sci確定），根據式（6）可知，c越大（θw越大），初始時激波匯聚增強越快（P2i越大）。

在向下游的匯聚過程中，由于激波波后流動方向不完全受壁面約束，式（6）將不再精確適用。因此，根據式（1）～式（4）計算得到的激波形狀r=r(x)（見圖4），再結合式（5）可以理論給出P2i的沿程分布。如圖5所示，在壁面前緣處（x/R= 0），P2i隨著θw的增加而增大，這與式（6）的描述相一致。前文圖4已經表明，在下游同一x/R位置處，當θw越大時，入射激波角增大，并且入射激波到軸線的距離更近。這也意味著激波面的曲率Sai和Sbi均增大。相應地，根據式（5）可知P2i也隨著增大（見圖5）。進一步表明了隨著θw的增大，內錐形激波匯聚增強得更快。換言之，在激波強度和激波面曲率的共同作用下，初始較強的激波（θw大）匯聚增強始終快于初始較弱的激波（θw小）。

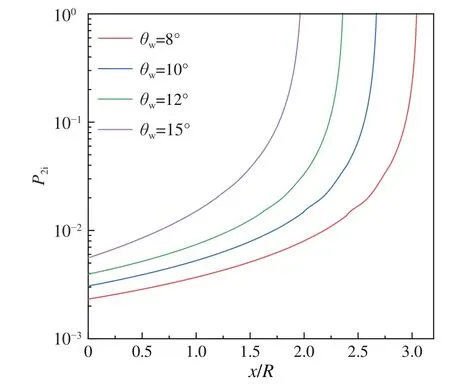
圖5 不同θw下軸對稱內錐形激波波后沿流線的無量綱壓力梯度分布(w/R = 1.5)Fig. 5 Distributions of the normalized pressure gradient behind the axisymmetric internal conical shocks at different θw (w/R = 1.5)

為了認識內錐形激波匯聚過程中激波自身強度的變化，如圖6所示，在數值模擬流場中沿著入射激波前緣到三波點提取了激波前后的壓比pi/p∞，并利用譚廉華等[19-20]的理論，由式（1）～式（4）給出了pi/p∞沿x/R的分布。圖6中理論和數值模擬獲得的pi/p∞分布整體符合較好，在接近三波點時，由于激波波后流線曲率較大[21]，理論結果存在一定的偏差。隨著下游激波強度的持續增大，在內錐形激波的匯聚過程中，必然會達到von Neumann強度，圖6中用虛線給出了本文Ma∞= 6條件下von Neumann準則對應的激波壓比pN/p∞≈ 9.67。在不同的θw下，內錐形激波匯聚增強的快慢不同（見圖5），導致入射激波上對應于von Neumann強度（pi/p∞=pN/p∞）的位置存在差異。在給定的θw下，根據式（1）～式（4）描述的入射激波形狀，可以得到入射激波上von Neumann強度的對應點（xN/R，rN/R）。

圖6 不同θw下軸對稱內錐形激波壓比的沿程分布(w/R = 1.5)Fig. 6 Pressure ratio distributions of the axisymmetric internal conical shocks at different θw (w/R = 1.5)

如圖7（a）所示，在θw= 7°～16°范圍內，利用式（1）～式（4）分別計算出了xN/R和rN/R隨θw的變化曲線，并且標記出了本文數值模擬流場中各θw工況對應的xN/R和rN/R位置。從圖7（a）可以看出，隨著θw的增大，xN/R減小，而rN/R迅速增大。進一步地，將這些由式（1）～式（4）計算出的（xN/R，rN/R），在（x/R，r/R）平面內依次展示，可以得到如圖7（b）所示的曲線。鑒于當入射激波強度達到von Neumann強度時，馬赫反射才有可能發生，因而圖7（b）中的（xN/R，rN/R）曲線和軸線（r/R= 0）共同限定了不同θw下允許馬赫盤存在的空間范圍。換言之，式（1）～式（4）為從理論上確定馬赫盤的位置提供了一種可能的途徑。

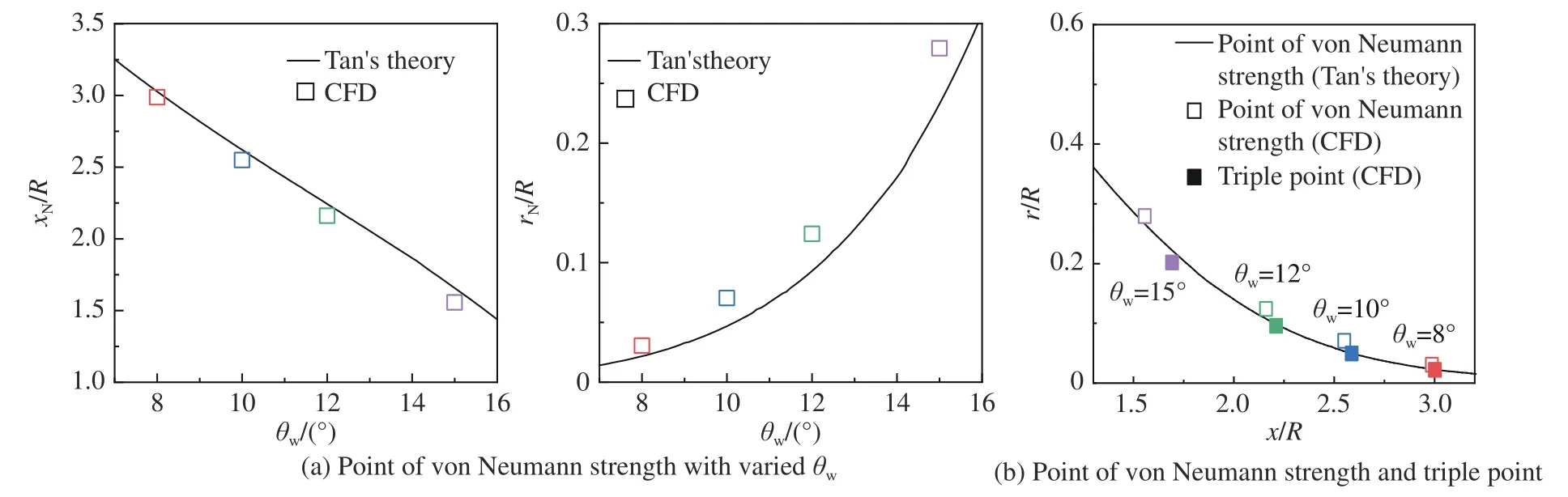
圖7 不同θw下von Neumann強度對應點和三波點(w/R = 1.5)Fig. 7 Point of von Neumann strength and triple point at different θw (w/R = 1.5)

為對比三波點與（xN/R，rN/R）之間的位置關系，從數值模擬流場中提取了不同θw下的三波點位置和von Neumann強度對應點的坐標，疊加在圖7（b）中。通過數值模擬結果可以看出，在不同的θw工況下，三波點均被約束在von Neumann強度對應點（xN/R，rN/R）的下游，兩者相距很近，但并不重合。隨著θw增大，軸對稱內錐形激波更快地達到von Neumann強度，但馬赫盤的位置并非完全依賴于激波匯聚增強過程。由此可見，僅通過式（1）～式（4）結合CST方程難以完全確定馬赫盤的位置，還需要考慮下游流動條件。

2.3 馬赫盤下游流動對其位置的影響

針對馬赫盤下游的流動問題，一般可以將滑移線SL包裹的流管（見圖3）視為準一維流動[11,34-36]。根據馬赫盤面積Am和流管內聲速喉道面積As，可以建立形如式（7）的等熵關系[11,26]：

式（7）中為緊鄰馬赫盤下游的氣流平均馬赫數。馬赫盤位置與其下游流動之間的匹配，往往可以通過聲速喉道來實現。

對于平面激波反射問題，已經發展出相應的幾何模型[11,26]來描述馬赫桿下游的流動。如圖8所示，起初從三波點T′發出的滑移線SL′具有恒定的角度（即三波點后氣流偏轉角）。緊接著，壁面尾緣產生的膨脹波穿過反射激波RS′后，作用在SL′上，使得SL′的角度連續減小（D′A′段），進而形成了聲速喉道。將這一幾何模型及相應的二維激波/膨脹波關系與式（7）相結合，即可確定馬赫桿MS′的位置[11,26]。這種方法為軸對稱內錐形激波反射問題中馬赫盤位置的確定，提供了極大的啟示。然而，在軸對稱內錐形激波反射流場中，馬赫盤下游的流動在受到壁面尾緣膨脹波干擾之前，先需要匹配反射激波后的非均勻壓力，導致滑移線經歷的變化比二維情況要復雜得多。因此，需要對軸對稱內錐形激波反射流場中馬赫盤下游流動進行深入考察。

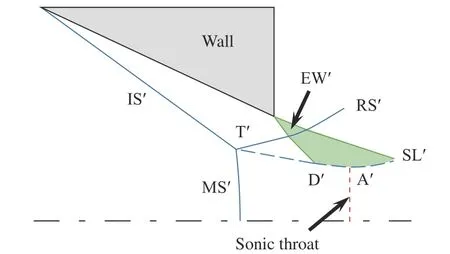
圖8 平面激波反射示意圖Fig. 8 Schematic of planar shock reflection

2.3.1 馬赫盤下游流動特征

首先關注壁面尾緣膨脹波干擾之前，馬赫盤下游的流動特征。對于不同的θw，當w/R充分大時（見表1），下游壁面尾緣產生的膨脹波離馬赫盤較遠，使得滑移線SL包裹的流管充分發展。根據流管自身能否演化形成聲速喉道，將馬赫盤下游流動劃分為兩類。

第一類工況：在壁面尾緣膨脹波干擾之前，馬赫盤下游滑移線SL包裹的流管能夠形成聲速喉道。θw= 8°或10°且w/R充分大時，均屬于此類工況。以θw= 10°、w/R= 3.5工況為例進行詳細分析。圖9展示了該工況下的流場局部無量綱壓力（p/p∞）云圖及其等值線，可以看到，入射激波IS和反射激波RS的波后壓力都是不均勻的。以穿過三波點T1的流線表征馬赫盤MD下游的滑移線SL，并以MD下游軸線（r/R= 0）上的馬赫數表征流管內的馬赫數分布，量化分析馬赫盤下游的流動特征。

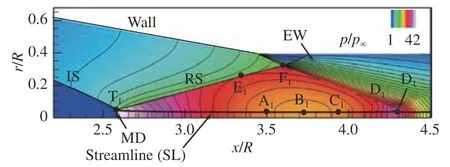
圖9 θw = 10°、w/R = 3.5工況數值模擬流場的局部無量綱壓力云圖Fig. 9 Local normalized pressure contours of the numerical flow field at θw = 10° and w/R = 3.5

圖10給出了SL包裹的流管面積A= πr2與馬赫盤面積Am之比的沿程變化情況，其中，xm為馬赫盤MD在軸線處的x坐標。同時，圖10中還疊加了流管內的馬赫數（Ma）分布，并標明了流管內首個聲速喉道的位置。結合圖9和圖10可知，SL包裹的流管從T1開始快速收縮，使得緊鄰馬赫盤下游的亞聲速氣流加速。在A1點處，流管內形成了聲速喉道。值得注意的是，在該工況下，壁面尾緣膨脹波與SL干擾的起始點D1不僅遠離聲速喉道A1，而且兩者之間還有超聲速區相阻隔。可見，聲速喉道A1的形成原因，是獨立于壁面尾緣膨脹波的。這與圖8中的平面激波反射流場存在本質差異。

圖10 θw = 10°、w/R = 3.5工況流管面積變化及其內馬赫數分布Fig. 10 Area ratio of the stream tube and distribution of Mach number in the stream tube at θw = 10° and w/R = 3.5

進一步地，圖11給出了反射激波RS（從T1點到F1點）波前、波后的壓力以及滑移線SL上（從 T1點到D1點）的壓力分布，以便于通過分析馬赫盤下游流動如何與反射激波后的非均勻壓力場相匹配，進而揭示馬赫盤下游滑移線SL包裹的流管內聲速喉道的形成原因。對比圖11和圖6可以看出，RS的波前壓力與入射激波IS波后壓力的變化趨勢并不一致。這是因為在軸對稱內收縮流場中，IS波后不同位置的氣流在到達RS之前，經歷了不同程度的等熵壓縮過程（見圖9）。這些氣流經過RS再次壓縮后，壓力呈先降低（見圖11的T1E1段）再升高（見圖11的E1F1段）的變化趨勢，而RS波后非均勻分布的壓力將直接影響馬赫盤下游的滑移線SL及流管形態。

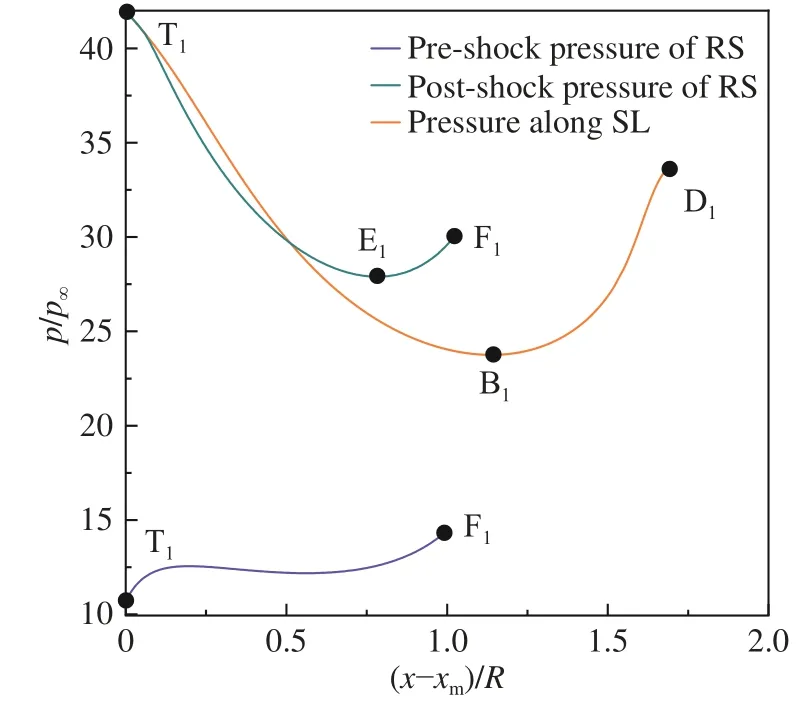
圖11 θw = 10°、w/R = 3.5工況反射激波前后及滑移線上無量綱壓力分布Fig. 11 Pre-shock and post-shock normalized pressure distribution of the reflected shock, and normalized pressure distribution along the slip line at θw = 10° and w/R = 3.5

從圖11可以看出，滑移線SL上T1B1段的壓力連續下降，以匹配RS在T1E1段的波后壓力；而滑移線SL上B1D1段的壓力連續上升，以匹配RS在E1F1段的波后壓力。結合圖10和圖11可知，在滑移線SL上T1B1段的降壓過程中，SL包裹的流管內原本亞聲速的氣流連續加速至超聲速。換言之，流管內聲速喉道的形成是匹配RS波后非均勻壓力的結果。RS和SL之間（見圖9中T1D1F1區域）通過等熵膨脹或壓縮來實現壓力變化，盡管這種變化關系不如二維平面激波反射流場那樣清晰，但從理論上建立分析方法仍然是將來值得嘗試的研究課題。

第二類工況：在壁面尾緣膨脹波干擾之前，馬赫盤下游滑移線SL包裹的流管無法形成聲速喉道。當θw增加至12°或更大（θw= 15°）且w/R充分大時，均屬于此類工況。圖12以θw= 12°、w/R= 3.0工況為例，展示了流場的無量綱壓力云圖。圖13給出了滑移線SL包裹的流管面積的沿程變化情況(A/Am)以及流管內的馬赫數分布。圖14展示了反射激波RS（從T2點到F2點）波前、波后的壓力以及滑移線SL上（從 T2點到A2點）的壓力分布。

圖12 θw = 12°、w/R = 3.0工況數值模擬流場的局部無量綱壓力云圖Fig. 12 Local normalized pressure contours of the numerical flow field at θw = 12° and w/R = 3.0

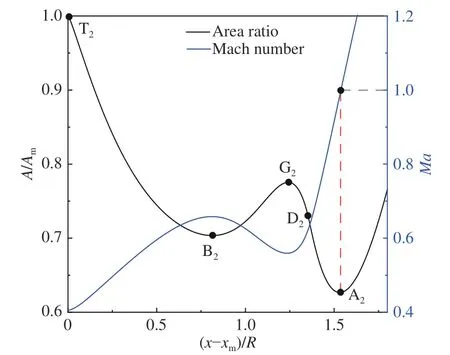
圖13 θw = 12°、w/R = 3.0工況流管面積變化及其內馬赫數分布Fig. 13 Area ratio of the stream tube and distribution of Mach number in the stream tube at θw = 12° and w/R = 3.0

與前文θw= 10°工況類似，馬赫盤下游流管內的壓力也需要匹配RS的波后壓力。有所不同的是，θw= 12°時RS在T2E2段的波后壓力（見圖14）不像θw= 10°工況那樣迅速降低（見圖11）。因而θw= 12°時馬赫盤下游流管內氣流的加速更為緩慢，以至于在壓力谷值點B2處，氣流仍未達到聲速（見圖13）。在B2點下游，由于要匹配RS在E2F2段波后壓力的升高，流管內的亞聲速氣流連續減速增壓（B2G2段），直至壁面尾緣膨脹波在D2點處對滑移線SL產生干擾。在馬赫盤下游流管內的亞聲速流動中，由于下游擾動能夠傳到上游，在D2點上游不遠處的G2點已經能夠感受到壁面尾緣膨脹波對SL的影響。由膨脹波帶來的壓力降低（見圖14），使得流管內的氣流急劇加速，直至在A2點處形成聲速喉道（見圖13）。可見，θw= 12°時馬赫盤下游流管內的氣流無法通過匹配RS的波后壓力達到聲速，而聲速喉道的形成依賴于壁面尾緣膨脹波對SL的干擾。

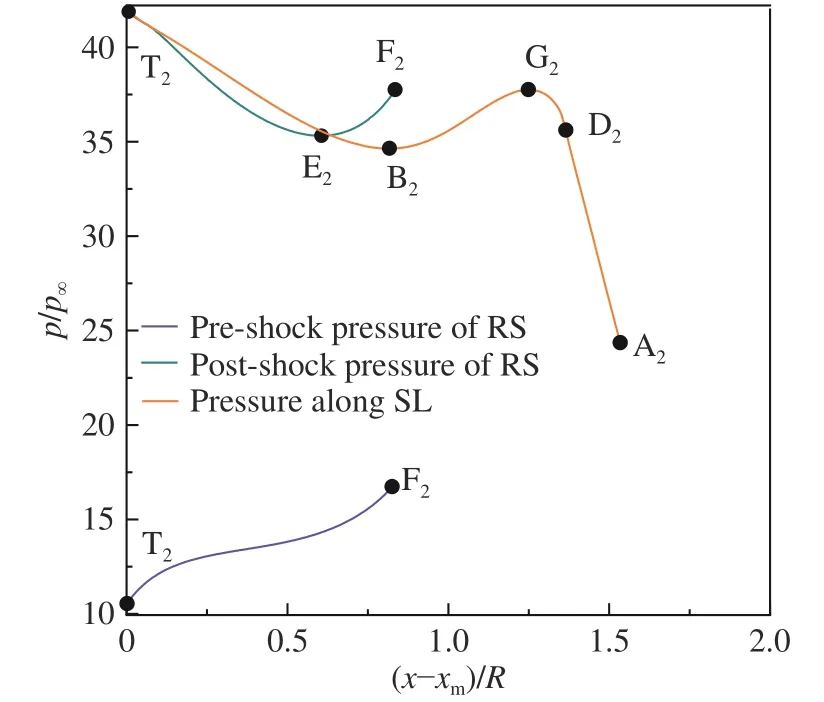
圖14 θw = 12°、w/R = 3.0工況反射激波前后及滑移線上無量綱壓力分布Fig. 14 Pre-shock and post-shock normalized pressure distribution of the reflected shock, and normalized pressure distribution along the slip line at θw = 12° and w/R = 3.0

綜上所述，在兩類馬赫盤下游流動中，反射激波RS波后壓力下降的快慢程度不同，導致馬赫盤下游流管內聲速喉道的形成過程存在是否依賴于壁面尾緣膨脹波的差異性。由于馬赫盤與聲速喉道之間具有如式（7）所示的平衡關系，馬赫盤位置對壁面尾緣膨脹波的依賴性也將不同。因此，需進一步考察壁面尾緣膨脹波對馬赫盤位置的影響。

2.3.2 膨脹波對馬赫盤位置的影響

在給定壁面前緣角度θw和入口半徑R的條件下，w/R決定了流場的內收縮比以及壁面尾緣膨脹波的存在區域。在本文關注的w/R范圍內，壁面尾緣膨脹波對馬赫盤下游流動產生干擾的位置隨著w/R的增加而向下游移動。

以θw= 10°為例，不同w/R工況下的入射激波及馬赫盤形狀如圖15所示。從圖15中馬赫盤局部區域（虛線框）的放大圖可以看出，不同w/R工況下，入射激波的形狀均重合，但馬赫盤位置存在差異。這種差異與2.3.1節討論的聲速喉道的形成機制緊密相關。

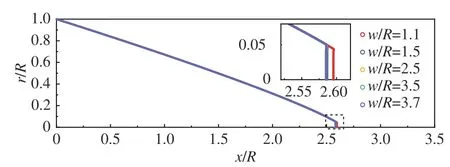
圖15 不同w/R下軸對稱內錐形入射激波及馬赫盤形狀(θw = 10°)Fig. 15 Shapes of axisymmetric internal conical shocks and Mach disks at different w/R (θw = 10°)

圖16提取了θw= 10°不同w/R工況中馬赫盤下游流管內的馬赫數分布，其中T1標明了三波點的位置。以壁面長度充分大的w/R= 3.5工況為參照，A1點標明了其聲速喉道的位置，而其他w/R工況下流管內的馬赫數分布從T1下游不同位置開始與w/R= 3.5工況產生差異。如2.3.1節所述，這種差異是由壁面尾緣膨脹波對滑移線產生干擾而導致的。在w/R= 1.1～2.0范圍內，壁面尾緣膨脹波對滑移線產生干擾的位置（圖16中三角符號）在A1點上游，并輔助馬赫盤下游流管迅速形成聲速喉道（圖16中矩形符號）。在w/R= 2.5～3.7范圍內，壁面尾緣膨脹波對滑移線產生干擾的位置在A1點下游，此時馬赫盤下游流管中聲速喉道形成于A1點，不依賴于壁面尾緣膨脹波。

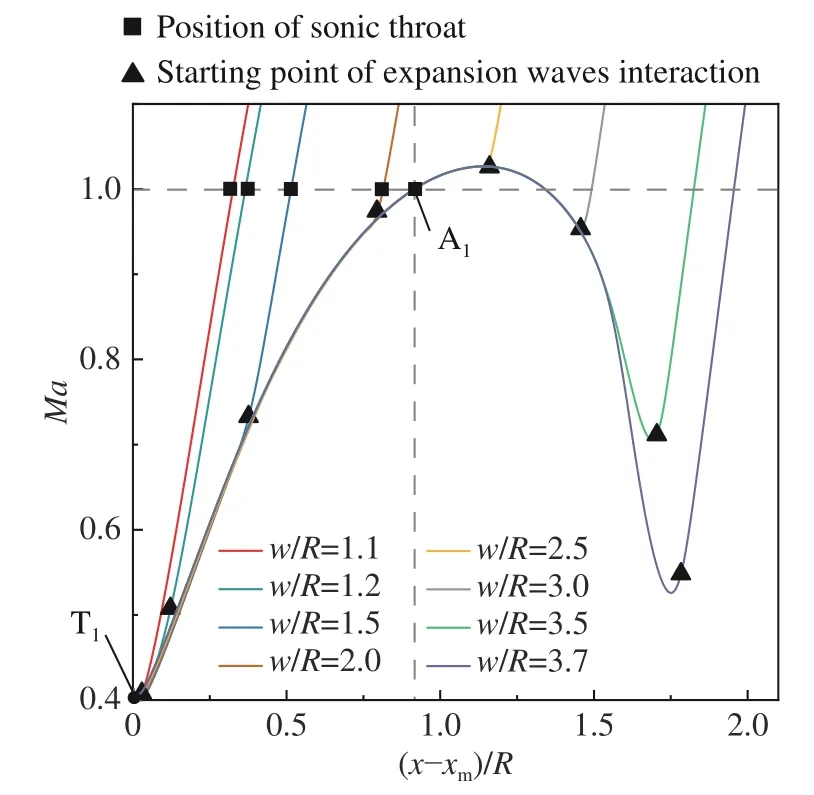
圖16 θw = 10°工況不同w/R下的流管內馬赫數分布Fig. 16 Distributions of Mach number in the stream tubes with different w/R at θw = 10°

進一步地，在θw= 10°工況下圖17（a）分別以w/R= 3.5時的馬赫盤位置xm*/R和聲速喉道位置xs*/R為參考值，給出了不同w/R工況的馬赫盤位置和聲速喉道位置的變化情況。可以看出，在w/R=1.1～2.0范圍內，隨著w/R增大，聲速喉道明顯向下游移動；同時，馬赫盤向上游移動。需要注意的是，馬赫盤位置的變化幅度遠小于聲速喉道位置的變化幅度。馬赫盤的位置僅在w/R＜ 1.5時變化明顯，在w/R＞ 1.5之后變化微小。結合前文2.2節可知，由于在軸線附近入射激波的形狀將越來越陡峭，馬赫盤位置的明顯移動，必然引起馬赫盤面積的大幅變化。

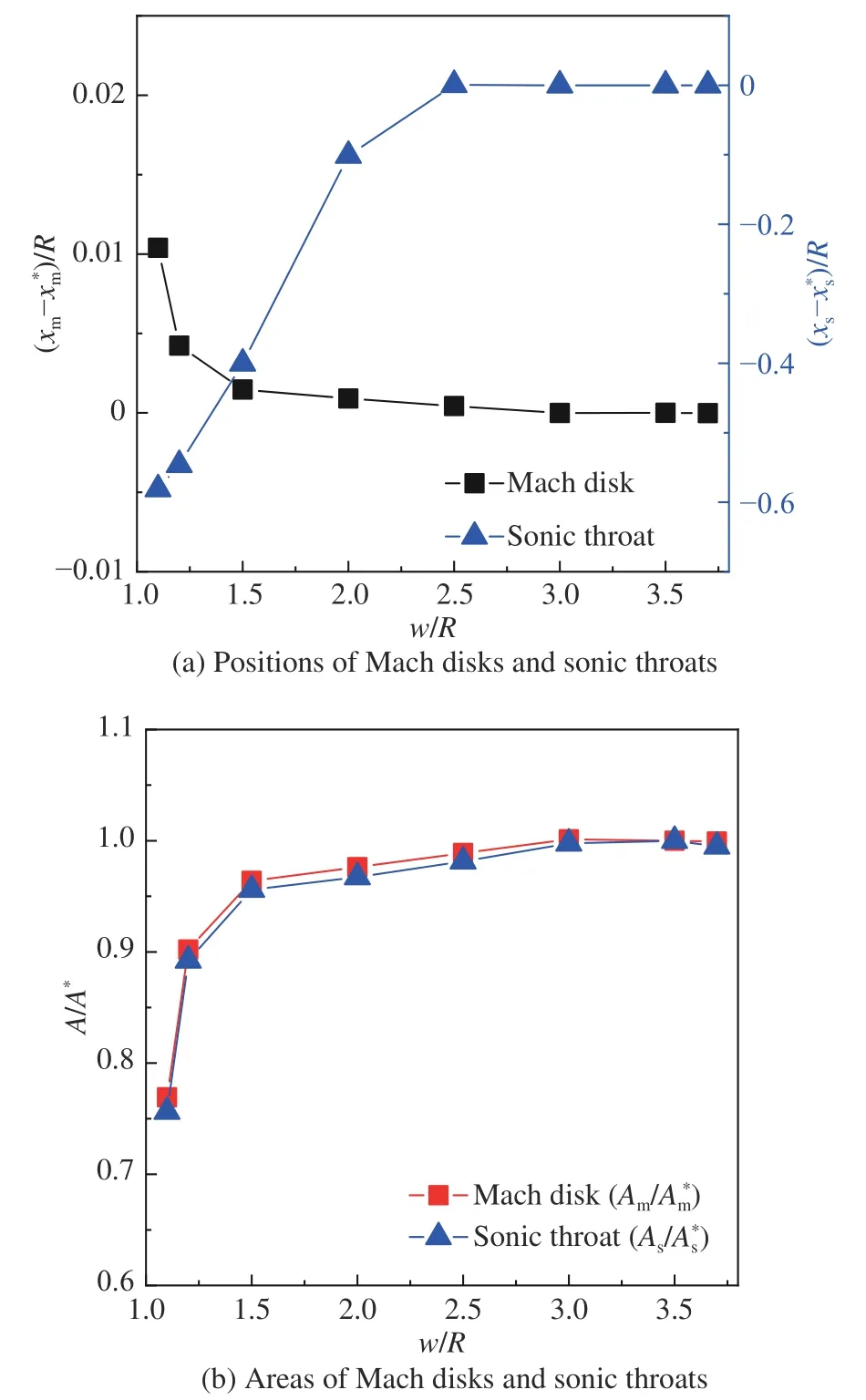
圖17 θw = 10°工況不同w/R下的馬赫盤、聲速喉道的位置和面積Fig. 17 Positions and areas of Mach disks and sonic throats with different w/R at θw = 10°

圖17（b）以w/R= 3.5時的馬赫盤面積Am*和聲速喉道面積As*為參考值，給出了不同w/R工況下的馬赫盤面積和聲速喉道面積的變化情況。可以看出，由于兩者遵循式（7）的關系，兩者的變化曲線幾乎重合。在w/R＜ 1.5時，馬赫盤面積和聲速喉道面積顯著減小；在w/R= 1.5～2.5范圍內，盡管聲速喉道的位置隨著w/R增大而向下游大幅移動（見圖17（a）），其面積變化卻很小（見圖17（b））。這主要是由于在w/R= 1.5～2.0范圍內，當壁面尾緣膨脹波入射滑移線時，馬赫盤下游流管內的氣流已經接近聲速，流管的微小面積變化也會使得流管內快速形成聲速喉道（見圖16）。在w/R= 2.5～3.7范圍內，聲速喉道的形成不依賴壁面尾緣膨脹波，因此，從圖17（a）和圖17（b）中可以看出，聲速喉道及馬赫盤的面積和位置，均基本保持恒定。類似地，在θw= 8°、w/R= 1.5～4.3工況下，壁面尾緣膨脹波不影響聲速喉道的形成。

對于θw= 12°和15°工況，在本文研究的w/R范圍內（見表1），馬赫盤下游流管內聲速喉道的形成均依賴于壁面尾緣膨脹波。圖18以θw= 12°工況為例，給出了不同w/R工況馬赫盤下游流管內的馬赫數分布。圖19（a）和圖19（b）分別展示了不同w/R工況馬赫盤、聲速喉道的位置和面積，其中，參考值xm*、Am*和As*均選自w/R= 3.0工況。結合圖18和圖19（a）可以看出，隨著w/R增加，壁面尾緣膨脹波入射位置向下游移動，聲速喉道的位置也隨之向下游移動，幾乎呈線性變化。然而，馬赫盤位置的變化幅度遠小于聲速喉道位置的變化幅度，馬赫盤向上游移動的趨勢逐漸減緩，在w/R＞ 1.5之后變化微小。從圖19（b）可以看出，馬赫盤和聲速喉道的面積同樣在w/R＞ 1.5之后變化很小。其原因與θw= 10°、w/R= 1.5～2.0工況下馬赫盤、聲速喉道面積趨于穩定的原因類似。

圖18 θw = 12°工況不同w/R下的流管內馬赫數分布Fig. 18 Distributions of Mach number in the stream tubes with different w/R at θw = 12°

圖19 θw = 12°工況不同w/R下的馬赫盤、聲速喉道的位置和面積Fig. 19 Positions and areas of Mach disks and sonic throats with different w/R at θw = 12°

在本文研究的軸對稱內錐流場中，馬赫盤下游聲速喉道的形成機制存在是否依賴于壁面尾緣膨脹波的兩類情況。對于不依賴壁面尾緣膨脹波的情況（如θw= 8°、w/R= 1.5～4.3工況以及θw= 10°、w/R=2.5～3.7工況），馬赫盤下游流管通過與反射激波后的非均勻壓力相匹配，進而形成聲速喉道；對于依賴壁面尾緣膨脹波的情況（如θw= 8°、w/R= 1.2工況，θw= 10°、w/R= 1.1～2.0工 況 以及θw= 12°和15°工況），馬赫盤下游流管還需要進一步匹配壁面尾緣膨脹波引起的壓力降低，才能夠形成聲速喉道。這種匹配關系，為理論求解馬赫盤位置提供了啟示。

2.4 馬赫盤位置的理論求解

結合2.2節和2.3節的分析可知，馬赫盤位于入射激波上von Neumann強度對應位置所限定的范圍內，而馬赫盤下游的流動還需要同時滿足反射激波下游的壓力變化以及準一維等熵關系式（7）。換言之，確定馬赫盤的位置需要求解反射激波下游的超聲速流場。最近，Shi等[25]發展的彎曲激波特征線方法（Method of curved-shock characteristics，MOCC）具有高效且精確求解超聲速流場的優勢。本節在給定來流和壁面前緣入口條件下，借助MOCC求解馬赫盤位置。

首先，假定馬赫盤處于入射激波上的von Neumann強度對應點（見2.2節）。利用MOCC，可以準確求解入射激波從壁面前緣到三波點的形狀，而且可以進一步獲得入射激波下游的超聲速流場，包括入射激波與反射激波之間的流場、反射激波形狀及其波后流場。滑移線作為反射激波波后邊界上的流線，其形狀在利用MOCC的求解過程中可以確定[37]。根據滑移線形狀，計算出滑移線包裹的流管面積，并找到流管面積的第一個最小值Asc。

上述滑移線形狀僅是基于反射激波下游的流場得到的，而反射激波下游壓力變化還需要與馬赫盤下游流管內的壓力相匹配。因此，利用準一維流動的等熵關系式（7），驗證馬赫盤下游流動是否符合2.3.2節中的描述。由于事先假定了馬赫盤位置，式（7）中的馬赫盤面積Am及流管內初始馬赫數均為已知量[19]，利用式（7）可以得到聲速喉道面積的理論值Ast。將Asc與Ast進行對比，若兩者之差在設定的誤差范圍內，則認為Asc是準確的，表明馬赫盤下游流動既能匹配反射激波波后的非均勻壓力變化，又滿足準一維流動的等熵關系，即假定的馬赫盤位置正確；若在設定的誤差范圍之外，則需要將假定的馬赫盤位置沿x方向調整后，重新計算一遍滑移線包裹的流管面積變化，并再次對比新獲得的Asc與Ast的值。如此迭代求解，直至最終得到馬赫盤的位置。

圖20以θw= 12°工況為例，利用上述理論方法求解了馬赫盤位置隨w/R的變化情況。作為對比，圖20中還給出了CFD流場中的馬赫盤位置。可以看出，理論與CFD結果吻合良好，兩者之間的最大差異僅為0.002。這表明，本節的理論方法，能夠準確地預測出馬赫盤隨w/R的變化。鑒于MOCC在理論求解效率和精度方面的獨特優勢，可望在更寬的來流條件和內錐幾何參數范圍內，快速預測馬赫盤的位置。

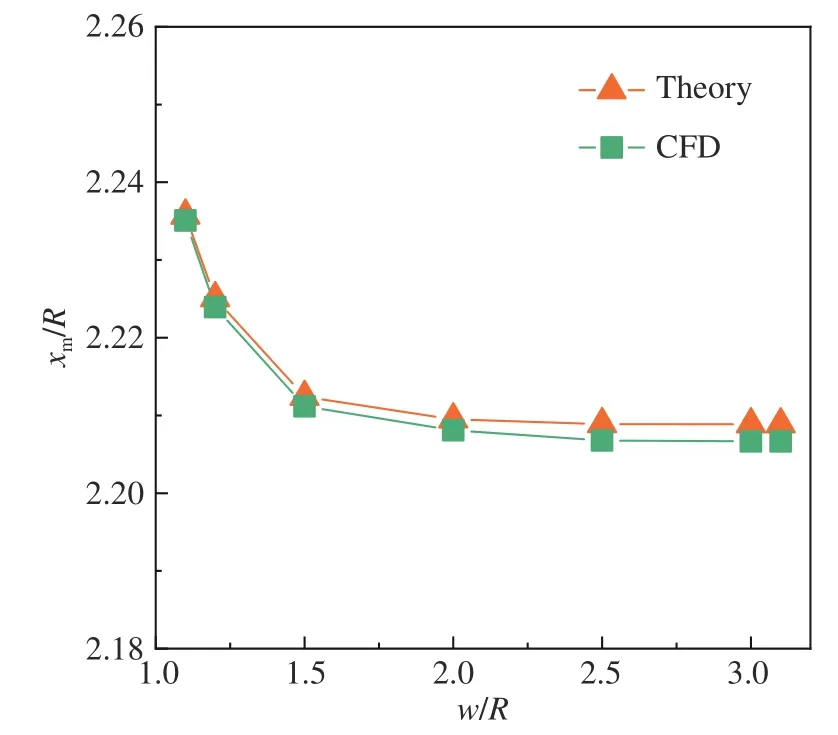
圖20 θw = 12°工況不同w/R下馬赫盤位置的理論和數值對比Fig. 20 Theoretical and numerical positions of Mach disks with different w/R at θw = 12°

3 結 論

在來流Ma∞= 6條件下，采用無黏數值模擬研究了軸對稱直內錐流動中影響馬赫盤位置的因素，主要得到了以下結論：

1）軸對稱內錐形入射激波自身的匯聚增強過程影響馬赫盤的位置。結合入射激波形狀理論與彎曲激波理論，闡明了隨著壁面前緣角度θw增大，入射激波的匯聚增強越快，并且能夠更快地達到von Neumann強度，該強度的對應位置限定了允許馬赫盤存在的空間范圍。

2）馬赫盤下游聲速喉道的形成機制存在是否依賴于壁面尾緣膨脹波的差異性，進而對馬赫盤位置產生不同的影響。當聲速喉道的形成不依賴于壁面尾緣膨脹波時，聲速喉道及馬赫盤的位置和面積均不隨w/R增大而變化。當聲速喉道的形成依賴于壁面尾緣膨脹波時，隨著w/R的增加，聲速喉道的位置向下游大幅移動，但聲速喉道及馬赫盤的面積逐漸趨于穩定。

3）將彎曲激波特征線方法與馬赫盤下游流管的準一維流動模型相結合，可以快速求解馬赫盤的位置。