反射激波沖擊單模界面的不穩(wěn)定性實驗研究

王宏輝，丁舉春，司 廷，羅喜勝

(中國科學技術(shù)大學 近代力學系，合肥 230026)

0 引 言

激波沖擊加載兩種不同密度流體的分界面后，界面上的初始擾動依次經(jīng)歷線性和非線性增長，與此同時，界面附近出現(xiàn)大量的尖釘（重流體侵入輕流體）、氣泡（輕流體侵入重流體）、旋渦等流動結(jié)構(gòu)，最終導致湍流混合的發(fā)生。這種界面不穩(wěn)定性通常被稱為Richtmyer-Meshkov（RM）不穩(wěn)定性[1,2]。已有的研究結(jié)果表明，斜壓渦量（密度梯度與壓力梯度不重合所致）和壓力擾動（激波穿過擾動界面后形成具有擾動的透射激波，波后呈現(xiàn)非均勻壓力場）是RM不穩(wěn)定性演化的主要物理機制[3-4]。RM不穩(wěn)定性不僅涉及激波動力學、旋渦動力學、可壓縮湍流等流體力學基礎(chǔ)難題，而且在慣性約束核聚變[5]、超燃沖壓發(fā)動機[6]、武器內(nèi)爆[7]等工程問題中具有廣泛的應用背景。因此，相關(guān)研究意義重大。

鑒于單模形狀的物質(zhì)界面具有數(shù)學描述形式簡單、普適性強（任意一個多模擾動可以看作是多個單模擾動的疊加）等特點，已有的研究（尤其是理論研究）多關(guān)注單模界面在平面激波沖擊下的不穩(wěn)定性發(fā)展[8-11]。Richtmyer[1]1960年首次提出激波誘導流體界面失穩(wěn)問題，并用界面的速度階躍近似表征激波的沖擊效應，推導得到了線性期擾動振幅增長的理論模型（后人稱之為沖擊模型）。隨著擾動振幅的逐漸增大，非線性效應增強（出現(xiàn)高階擾動模態(tài)），界面演變成非對稱的尖釘和氣泡結(jié)構(gòu)，擾動增長率持續(xù)降低，此時沖擊模型失效。為了準確描述非線性期的擾動增長，Zhang 和 Sohn[10-11]基于擾動展開方法對界面兩側(cè)流體的運動學和動力學方程進行展開，獲得了擾動增長的高階非線性模型。近年來，Zhang和Guo分析發(fā)現(xiàn)尖釘和氣泡的無量綱振幅增長規(guī)律十分相似，并基于此提出了一種全新的非線性勢流模型（ZG模型）[12]。需要指出的是，以上介紹的理論模型均只適用于初始小擾動（即初始振幅波長比小于0.1）界面的演化發(fā)展。Dimonte和Ramaprabhu基于大量的數(shù)值模擬結(jié)果總結(jié)規(guī)律，提出了一種適用于大擾動界面發(fā)展的經(jīng)驗模型[13]。

實驗研究不僅可以發(fā)現(xiàn)新的物理現(xiàn)象和規(guī)律，而且可以檢驗理論模型的正確性以及驗證數(shù)值算法的可靠性。因此，在RM不穩(wěn)定性研究歷程中，實驗研究一直起著舉足輕重的作用。Meshkov[2]采用硝化纖維膜隔離兩種不同氣體以形成單模形狀的氣體界面，首次開展了RM不穩(wěn)定性驗證實驗，實驗結(jié)果初步證實Richtmyer理論分析的正確性。然而，實驗中硝化纖維膜的支撐以及破膜后的碎片對界面演化產(chǎn)生嚴重的干擾，導致實驗中的擾動增長率明顯低于沖擊模型的預測值。后來，Jacobs等[14-15]從實驗段的上下兩端分別充入不同密度的氣體，讓兩種氣體在實驗段中間相遇并隨后從側(cè)壁上的縫隙流出，形成一個相對穩(wěn)定的氣體界面。而且，他們發(fā)現(xiàn)可通過在實驗段管壁上施加一個固定頻率的水平振動的方法形成一道單模形狀的氣體界面。這種界面形成方法雖然避免了硝化纖維膜帶來的一系列干擾，但生成的氣體界面具有三維性和擴散性，且界面附近存在非均勻速度場，這些因素同樣會對界面演化產(chǎn)生不利影響。考慮肥皂膜具有厚度薄、對流場污染小、形狀維持久等特點，Liu等利用細絲約束肥皂膜技術(shù)[9]生成了更為理想的間斷型單模氣體界面，有效消除了氣體擴散層、三維性、硝化纖維膜碎片等不利因素的影響，獲得了平面激波誘導輕/重單模界面失穩(wěn)的高置信度實驗結(jié)果，并利用實驗結(jié)果檢驗了已有理論模型的準確性，發(fā)現(xiàn)ZG模型相比其他非線性模型具有更好的預測能力。

已有的理論、實驗和數(shù)值研究多關(guān)注擾動界面在入射激波單次沖擊下的不穩(wěn)定性發(fā)展。實際工程應用往往涉及一個密閉系統(tǒng)，存在于密閉系統(tǒng)中的激波必然會和固壁作用生成反射激波，因此密閉系統(tǒng)中的物質(zhì)界面除了受到入射激波的沖擊外還會受到反射激波的二次甚至多次沖擊，發(fā)生十分復雜的不穩(wěn)定性演化。比如在慣性約束核聚變中，入射球形激波穿過氘氚冰/氘氚氣體界面后形成一道向內(nèi)傳播的透射激波，透射激波到達靶丸中心立即生成一道反射激波，隨后反射激波向外傳播并再次作用正在演化的物質(zhì)界面，導致復雜界面不穩(wěn)定性和湍流混合的發(fā)生。另外，在高超聲速飛行器的發(fā)動機內(nèi)流中，激波在燃燒室內(nèi)壁來回反射生成多道反射激波，燃料在向下游運動過程中依次穿過這些反射激波，發(fā)生復雜的界面不穩(wěn)定性演化，并伴隨著燃料與氧氣的快速混合。可見，反射激波誘導的界面失穩(wěn)和湍流混合是工程中廣泛存在且十分重要的流動問題。與單次激波誘導的界面失穩(wěn)不同，反射激波的二次沖擊會在界面上沉積相同或相反方向（相對于入射激波沉積的渦量的方向）的附加渦量以及額外的壓力梯度，從而導致新的流動結(jié)構(gòu)（如射流、小尺度渦結(jié)構(gòu)等）和現(xiàn)象（界面反相）的出現(xiàn)[16-17]。另外，已有的研究證實，反射激波沖擊后的界面流動更易發(fā)生轉(zhuǎn)捩，導致湍流混合的提前發(fā)生[18]。由于反射激波沖擊前物質(zhì)界面已經(jīng)處于演化狀態(tài)并發(fā)生嚴重扭曲，且界面附近的流場參數(shù)未知，因此相關(guān)流動機理分析非常困難。至今，反射激波誘導下的界面演化機制、流動轉(zhuǎn)捩條件以及湍流場特性仍是流體力學界公認的難題之一。可見，開展反射激波誘導的界面不穩(wěn)定性研究亦具有十分重要的科學意義。

本文基于Liu等發(fā)展的肥皂膜技術(shù)[9]生成單模形狀的空氣/六氟化硫（air/SF6）界面，借助高速紋影技術(shù)捕捉入射和反射激波沖擊界面后的詳細不穩(wěn)定性演化過程，重點分析反射距離對不穩(wěn)定性發(fā)展的影響，并利用實驗結(jié)果檢驗已有的經(jīng)驗模型。

1 實驗方法

實驗在改進后的水平激波管內(nèi)開展。如圖1（a）所示，該水平激波管由高壓段、低壓段和實驗段組成，其中高壓段長1.7 m，低壓段長2.0 m，實驗段長0.37 m，實驗段截面積為260 mm × 80 mm，實驗段觀察窗面積為275 mm × 100 mm。實驗時，采用一個塑料膜片將高壓段和低壓段隔開，利用壓氣機向高壓段充入空氣，當壓力達到破膜臨界值時，膜片破裂，產(chǎn)生一道向下游傳播的平面激波（馬赫數(shù)為1.22 ± 0.02）和一道向上游傳播的稀疏波。

圖1 實驗步驟示意圖Fig. 1 Sketch of the experimental setup

如圖1（b）所示，實驗的界面生成裝置分為A、B兩部分，每部分裝置采用5 mm厚的亞克力板雕刻組裝而成，其中上下兩塊亞克力板的垂直距離為6 mm，即實驗段內(nèi)高6 mm。裝置A和B的連接面為正弦形狀，其上下亞克力板內(nèi)表面（緊鄰正弦面）均嵌入一條具有相同正弦形狀的細絲以約束肥皂液的運動，每條細絲凸出實驗段不超過0.2 mm，已有的實驗結(jié)果證明這樣微小的細絲對流場的影響可忽略不計。實驗中，首先采用少量肥皂液（由質(zhì)量分數(shù)78%的蒸餾水、2%的油酸鈉、20%的甘油配制而成）將裝置B的正弦細絲潤濕，然后將沾有適量肥皂液的矩形小刷子沿濕潤的細絲表面緩慢移動，即可生成正弦形狀的肥皂膜界面。為了生成air/SF6氣體界面，需要往界面右側(cè)空間緩慢充入SF6氣體（在此過程中，需要維持肥皂膜界面穩(wěn)定、不變形）。具體地說，將兩個沾有肥皂液的導氣管輕輕插入肥皂膜（用細針刺破導氣管內(nèi)部的肥皂膜），通過其中一個導氣管（進氣口）向裝置B充入SF6氣體，使得air從另一個導氣管（出氣口）排出，最終裝置B內(nèi)部充滿高濃度的SF6氣體。實驗中，用氣體濃度儀實時檢測出氣口的氧氣濃度，當氧氣濃度低于1%時，認為air幾乎被全部排出，停止充氣。隨后，抽出兩個導氣管，將裝置B緩慢放入激波管實驗段直至與裝置A完全接觸。需要強調(diào)的是充氣過程持續(xù)約40 s，在這樣的短時間內(nèi)只有少量氣體分子穿過肥皂膜到達界面另一側(cè)，因此生成的界面可以看作是一個理想的間斷型氣體界面。實驗段末端是固壁，入射激波穿過air/SF6氣體界面后形成的透射激波，到達激波管末端生成一道向上游傳播的反射激波，實現(xiàn)二次沖擊界面的目的。實驗采用高速紋影技術(shù)捕捉激波和界面相互作用的全過程，高速相機（FASTCAM SA5，Photron Limited）的拍攝頻率設(shè)為50 000 幀/s，曝光時間為1 μs。

2 結(jié)果與分析

定義初始界面平衡位置和激波管尾端壁面的距離為反射距離，考慮四種不同反射距離下air/SF6單模界面在反射激波沖擊后的不穩(wěn)定性發(fā)展，重點研究反射距離對不穩(wěn)定性發(fā)展的影響。表1給出了各組工況的初始參數(shù)，其中：A1+表示初始激波波后Atwood數(shù)，L0表示初始界面平衡位置與尾端固壁之間的距離，λ0和a0分別表示初始界面的波長和振幅，VFS是界面右側(cè)SF6氣體濃度，Vi1、Vt1和ΔV1是入射激波速度、透射激波速度以及激波沖擊導致的界面階躍速度。艾特伍德 數(shù)被定義為A= (ρ2?ρ1)/(ρ2+ρ1)，其中ρ1和ρ2分別表示界面左、右側(cè)的初始氣體密度。表2給出了反射激波沖擊界面前的主要流場參數(shù)，其中：A2+表示初始激波波后Atwood數(shù)，λ20、a20和a' (t1)分別表示反射激波到達時界面的波長、振幅及振幅增長率，Vi2、Vt2和V20分別表示反射激波速度、第二道透射激波速度以及反射激波沖擊后的界面速度。

表1 不同工況中入射激波沖擊界面的初始參數(shù)Table 1 Initial flow parameters

表2 反射激波沖擊界面前的流場條件Table 2 Flow parameters at the reshock

2.1 界面演化

圖2給出了四組不同工況中air/SF6單模界面在入射和反射激波沖擊后的演化紋影圖像。對于四組工況，激波和界面的演化結(jié)構(gòu)均十分清晰，且在整個演化過程中界面保持良好的對稱性，證明了實驗方法的可行性和可靠性。這里以工況120-20-1為例，詳細介紹激波沖擊單模界面后的不穩(wěn)定性演化過程。定義入射激波（IS）到達初始擾動界面（Ⅱ）平衡位置的時刻為零時刻。由于界面兩側(cè)氣體的聲阻抗（密度與聲速的乘積）不同，入射激波穿過air/SF6界面后，產(chǎn)生一道向下游運動的透射激波（TS）和一道向上游運動的反射激波。與此同時，界面受入射激波的沖擊獲得一個階躍速度，向下游運動。隨后，氣體界面（MI）離開約束條，呈現(xiàn)較為理想的單模形狀，并在斜壓渦量誘導下持續(xù)變形，導致界面振幅不斷增大。需要指出的是，生成的透射激波TS是具有初始擾動的（近似正弦形狀），其在向下游傳播過程中逐漸恢復為一道均勻的平面激波，最后到達實驗段尾端壁面，生成一道向上游運動的反射激波（RS）。反射激波RS會再次作用正在演化的氣體界面（997 μs，此時界面依然可以看作是二維的），導致界面失穩(wěn)加劇。

圖2 不同反射距離下激波和單模界面的相互作用過程Fig. 2 Interaction of shock wave with a single-mode interface for different cases

對于工況200-20-1，反射激波再次作用界面前，界面在入射激波的沖擊下已演化較長時間，呈現(xiàn)出較多的小尺度結(jié)構(gòu)和顯著的三維性。由于界面振幅較大，反射激波經(jīng)過界面時在尖釘處發(fā)生復雜的激波-激波干擾。反射激波沖擊界面后（1109 μs），產(chǎn)生向上游傳播的透射激波（RST）、向下游傳播的反射稀疏波以及展向傳播的橫波，這些橫波會持續(xù)作用界面一段時間。隨后，界面振幅逐漸降低，直至界面反相的發(fā)生（工況80-20-1，779 μs）。對于工況200-20-1，反射激波作用前，界面振幅已經(jīng)較大，在隨后的反相過程中界面發(fā)生嚴重扭曲，已不是規(guī)則的單模界面（1679 μs），界面厚度（氣體混合）急劇增加。反相之后，界面附近的流場更為紊亂，界面兩側(cè)氣體的混合加速。

2.2 界面振幅

實驗獲得的清晰界面結(jié)構(gòu)有助于準確測量界面的擾動振幅。圖3給出了四組不同工況下界面擾動振幅隨時間的變化。可以看出，四組工況中的界面振幅變化規(guī)律非常相似。入射平面激波沖擊單模界面后，界面振幅首先經(jīng)歷線性增長，在此階段界面保持正弦形狀（圖2）。對于本文的四種工況，反射激波作用界面前，擾動振幅增長曲線基本重合，這是因為四組工況的初始條件相同（只是邊界條件不同），這也說明了實驗結(jié)果具有較高的可重復性。表3給出了實驗測量的線性增長率和理論預測結(jié)果，從中發(fā)現(xiàn)，實驗測量值略低于沖擊模型預測值。這種差異可歸因于肥皂膜破碎后的液滴、激波管壁面效應等實驗因素的影響，以及無黏、不可壓縮流動等模型推導過程中的假設(shè)和簡化。隨著擾動振幅的不斷增大，非線性效應增強，界面上出現(xiàn)高階擾動模態(tài)，擾動增長率逐漸降低，此時界面演化成非對稱的尖釘和氣泡結(jié)構(gòu)。由于四組工況中的反射距離不同，反射激波再次作用的時間亦不同。對于工況40-20-1，當τ= 1.2時，反射激波再次作用處于演化中的界面，界面振幅受反射激波壓縮迅速減小，隨后逐漸減小為零（反相），最后在相反方向上快速增長。需要指出的是，對于本文的四種工況，反射激波作用界面時，界面演化均已進入非線性期。四組工況下，反射激波作用界面后，擾動振幅快速增加且?guī)缀蹼S時間線性增長。通過擬合實驗數(shù)據(jù)，可以得到反射激波沖擊后的擾動增長率，如表4所示。

圖3 擾動振幅隨時間變化的無量綱結(jié)果Fig. 3 Variations of dimensionless amplitudes with time for different cases

表3 不同反射距離下入射激波沖擊后的線性增長率實驗值和理論預測對比Table 3 Comparison of the linear growth rates between experimental results and theoretical predictions

表4 關(guān)于反射激波作用后的擾動振幅增長率的實驗測量值和理論預測值對比Table 4 Comparison of the post-shock growth rates between the experimental results and theoretical predictions

從表4可以看出，對于反射距離為40 mm、80 mm和120 mm三組工況，反射激波作用后的擾動振幅增長率十分接近。由此可見，在一定的反射距離范圍內(nèi)，反射激波作用后的擾動增長率幾乎與反射距離無關(guān)，即與反射激波作用前的擾動振幅和增長率無關(guān)。需要強調(diào)的是，對于反射距離非常小（與擾動振幅一個量級）的情形，反射激波作用界面產(chǎn)生的新的波系在界面和壁面之間來回反射，必將對界面演化產(chǎn)生持久且顯著的影響，不過，這不在本文的研究范圍之內(nèi)。對于反射距離較大的工況（200 mm），反射激波作用后的擾動振幅增長率略低于其他三組工況。可能的原因有兩個：1）隨著反射距離的增加，反射激波接觸界面前，界面已經(jīng)呈現(xiàn)許多小尺度結(jié)構(gòu)，并具有一定的三維性；2）由于界面振幅已經(jīng)增長得較大，反射激波在穿過界面過程中發(fā)生復雜的波系干擾，產(chǎn)生較強的局部壓力擾動，抑制界面振幅發(fā)展。

反射激波誘導的界面不穩(wěn)定性不僅包含經(jīng)典RM不穩(wěn)定性的主要物理過程（復雜波系和斜壓渦量的生成），而且還伴隨著激波-激波干擾、激波和旋渦相互作用等復雜物理現(xiàn)象的發(fā)生。對于這樣的復雜問題，很難進行純粹的理論建模。根據(jù)已有的實驗和數(shù)值模擬結(jié)果，學者們提出了兩類經(jīng)驗模型。一類是Mikaelian模型[19]，適用于三維多模態(tài)界面在反射激波沖擊后的演化，可描述為：

其中，h2表示反射激波作用后界面整體混合寬度（本文中為尖釘頭部和氣泡頭部的距離，其大小是振幅的兩倍）， ?V2是反射激波沖擊引起的界面階躍速度（其反映反射激波的強度），A+2是反射激波波后的Atwood數(shù)。式（1）表明，反射激波沖擊后的界面混合寬度增長率與A+以及激波強度成正比，而與反射激波沖擊前的振幅增長率無關(guān)。Mikaelian根據(jù)大量的數(shù)值模擬結(jié)果求得經(jīng)驗系數(shù)C= 0.28。后來，學者們進一步研究發(fā)現(xiàn)，C的取值與反射激波作用前的界面演化程度相關(guān)[16-17]。將反射距離較小的三組工況的實驗數(shù)據(jù)代入式（1），求得C值在0.7左右，而大距離工況的C值明顯低于0.7。這說明，給定合適的經(jīng)驗系數(shù)，Mikaelian模型對小反射距離下的二維單模界面的演化也能給予有效的預測。

另一種經(jīng)驗模型是Charakhch'an模型[20]，適用于反射激波沖擊二維單模界面的不穩(wěn)定性問題，可描述為：

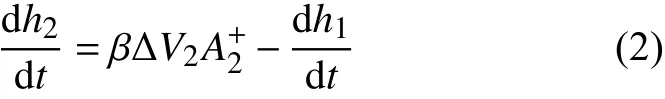
其中，h1是反射激波作用前界面的混合寬度。對于本文的四組工況，反射激波作用前，擾動界面均呈現(xiàn)清晰的二維結(jié)構(gòu)，因此，相比Mikaelian模型，式（2）更適合預估本文實驗中反射激波作用后的擾動增長率。Charakhch'an基于數(shù)值模擬結(jié)果，測得 β值在0.53～1.5之間，最終取平均值1.25。由于反射激波沖擊二維單模界面的相關(guān)實驗結(jié)果非常少，式（2）中的 β值一直沒有得到實驗結(jié)果的充分檢驗。本文的實驗結(jié)果提供了一個檢驗 β值的良好機會。如表4所示，對于反射距離較小的三組工況，經(jīng)驗系數(shù) β的值在0.83左右，這與Ukai[17]計算得到的 β值（在0.59～0.84之間，平均值為0.68）比較接近。然而，大距離工況的 β值僅為0.47。以上分析說明，采用恰當?shù)慕?jīng)驗系數(shù)，Mikaelian模型和Charakhch'an模型均能對反射激波作用后的擾動增長率給予合理預測。另外，兩種模型的經(jīng)驗系數(shù)對反射激波作用前的界面演化狀態(tài)較為敏感，如果某一初始條件（如反射距離）的改變引起了界面演化狀態(tài)的變化，必須采用新的經(jīng)驗系數(shù)值。

3 結(jié) 論

本文采用線約束肥皂膜技術(shù)生成了較為理想的間斷型air/SF6單模氣體界面，獲得了平面激波及其反射激波沖擊下單模界面的不穩(wěn)定性發(fā)展全過程，測量得到擾動振幅的發(fā)展規(guī)律，重點考察了反射距離對不穩(wěn)定性發(fā)展的影響。研究發(fā)現(xiàn)：

1）在一定的反射距離范圍內(nèi)（不包括極小反射距離情形），反射激波作用后的擾動增長率幾乎與反射距離無關(guān)，即與反射激波作用前的擾動振幅和增長率無關(guān)。隨著反射距離的進一步增大，反射激波作用界面后的振幅增長率降低。

2）采用恰當?shù)慕?jīng)驗系數(shù)，Charakhch'an模型和Mikaelian模型均能對反射激波作用界面后的擾動增長率給予有效預測。以上兩種模型的經(jīng)驗系數(shù)對反射激波作用前的界面演化狀態(tài)較為敏感，如果反射距離的改變引起/（不引起）界面演化狀態(tài)的變化，需要/（不需要）改變經(jīng)驗系數(shù)的值。