弓形卸扣本體受力計算公式探討

姜明遠，王寶中，林風梅

(1.華北理工大學 機械工程學院，河北 唐山 063009；2.巨力索具股份有限公司，河北 保定 071000)

0 引言

卸扣是吊索具的一種，在中國是一個十分有發展前景的產品。卸扣的應用范圍非常廣泛，適用于各個工業制造、大型吊裝和工程建設領域。早期，由于國內對卸扣的材料和結構研究不夠深入，缺乏在安全設計系數下的可靠設計方法，只能依靠國外的樣本進行模仿制造[1]。現如今，對卸扣的研究更近一步，蔡裕民在《吊裝工藝計算近似公式及應用》中提出了計算D形卸扣最大應力的公式。弓形卸扣比D形卸扣具有更強的承載力和更精美的外觀，應用更為廣泛。由于弓形卸扣受力情況較為復雜，所以現在還沒有針對弓形卸扣最大應力的計算公式。本文探討同樣額定載荷下D形卸扣的計算公式可否用于或在什么樣的條件下可以用于弓形卸扣最大應力計算，以巨力索具公司額定載荷為9.5 t的弓形卸扣為例，通過用ANSYS Workbench進行有限元分析的方法來模擬受力情況，對比仿真結果和計算結果，為得到弓形卸扣本體最大應力的計算公式提供理論依據。

1 產品基本信息

巨力索具公司額定載荷為9.5 t的弓形卸扣如圖1所示,其吊環螺釘和銷軸是螺紋聯接，即將吊環螺釘擰入銷軸中。

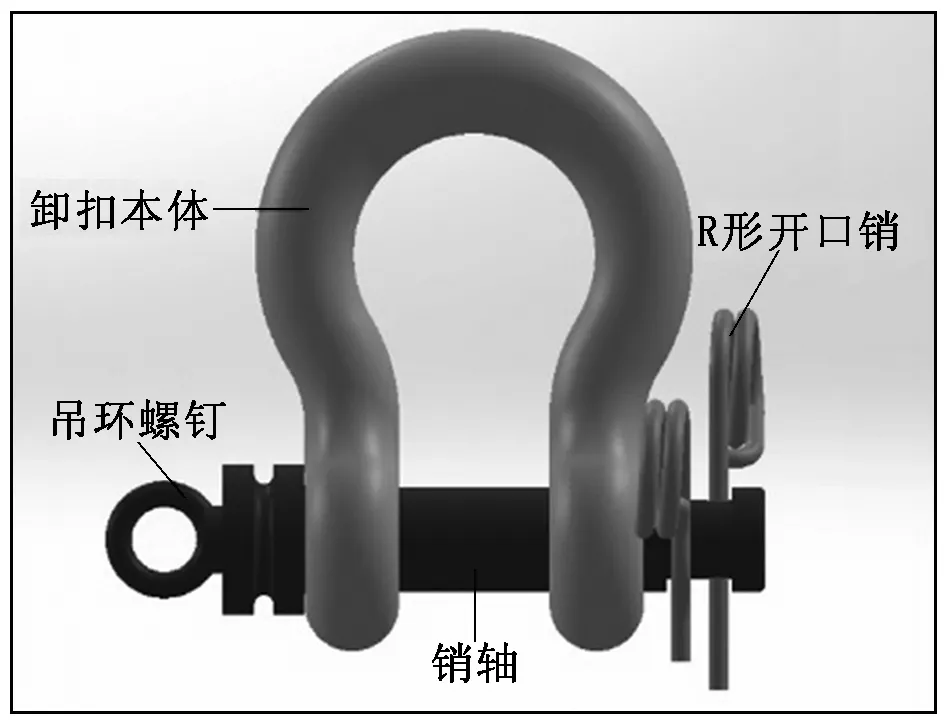
圖1 巨力索具公司額定載荷9.5 t的弓形卸扣

該弓形卸扣的重量為4.25 kg，額定載荷為9.5 t，卸扣本體和銷軸采用的材料為34CrNiMo6，其屈服應力σs≥760 MPa、抗拉極限σb≥1 075.2 MPa。卸扣本體和銷軸所用材料屬于合金鋼類材料，分析設定材料信息時取相同的參數，合金鋼的性能參數為：密度7 850 kg/m3，彈性模量206 GPa，泊松比0.3。

2 有限元分析計算

2.1 有限元模型的建立

選用ANSYS Workbench軟件中的static structural模塊進行有限元分析[2]。通過三維建模軟件SolidWorks對此卸扣進行建模，由于在實際工況中吊環螺釘、R形開口銷在吊裝過程中不受力，所以分析時將其抑制，在后面的分析中不對其進行分析，從而簡化模型，減少運算過程的計算量，提高仿真模擬準確性。該卸扣用于吊裝作業，卸扣本體上端與20 t高強度環形吊帶連接，吊帶厚度約38 mm、寬度約70 mm，通過static structural模塊中的Design Modeler在卸扣本體上端分割一個寬度為70 mm的表面，在這個表面上施加豎直向上的力來代替卸扣本體上端與20 t高強度環形吊帶連接的受力。卸扣的銷軸與Crosby公司的M24×36吊環螺釘相連，將吊環螺釘的底部設為固定面[3]。卸扣受力面如圖2所示，卸扣固定面如圖3所示。

圖2 卸扣受力面

圖3 卸扣固定面

2.2 定義接觸類型

在Model環境中定義卸扣的接觸類型。根據實際的工況，卸扣的接觸類型設置如表1所示。表1中，Bonded為綁定接觸，No Separation為不分離接觸。

表1 卸扣的接觸類型設置

2.3 劃分網格

根據產品外形特點，在ANSYS Workbench中選取四面體網格中的Patch Independent方法來對卸扣本體和銷軸進行網格劃分，這種網格劃分方法能很好地劃分連接面之間的過渡區域，得到較好的網格劃分結果[4]。由于吊環螺釘不是這個仿真分析的主要部件，故將吊環螺釘用自動劃分網格的方式來劃分網格。劃分質量較好的網格可以滿足后續的分析需求，網格劃分質量報告如圖4所示。圖4中，橫坐標表示的是網格度量。網格度量以1為最大，越接近1說明網格質量越好。

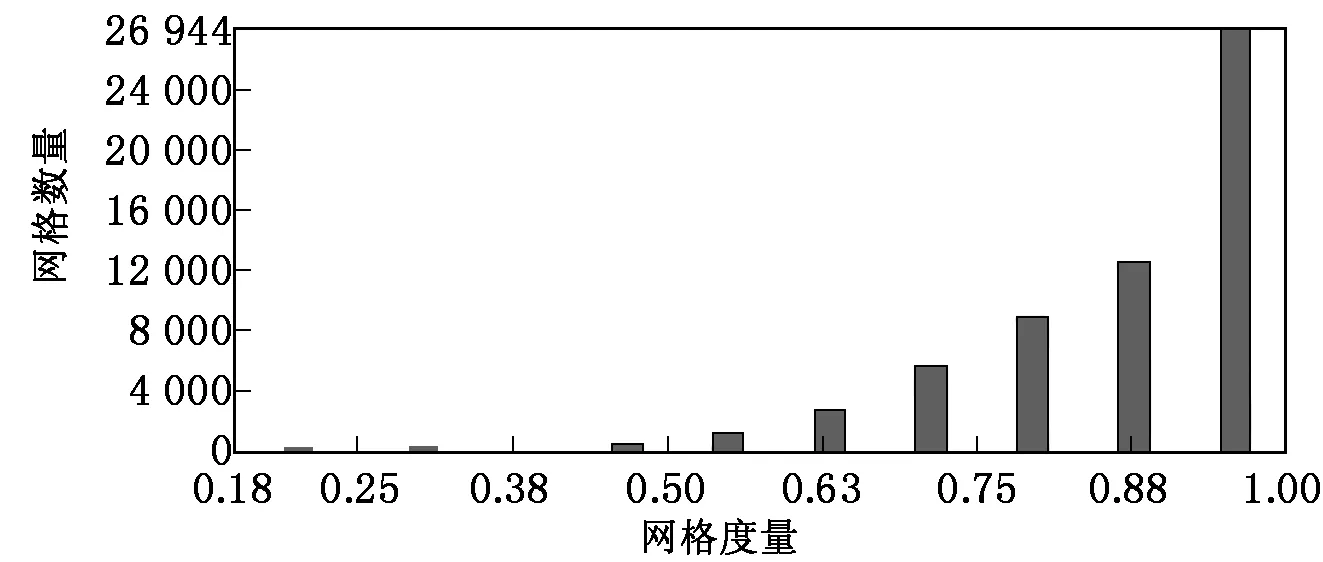
圖4 網格質量

3 受力模擬分析

在卸扣受力面上分別施加2.5 t、5 t、7.5 t、9.5 t、12.5 t、15.5 t、18 t、19 t、23 t、27 t、31 t、35 t、38 t、40 t的載荷，得到卸扣本體最大應力數值，如表2所示。

以施加載荷9.5 t為例進行說明，9.5 t載荷相當于93 100 N的力，在Workbench軟件中輸入力93 100 N，得到如圖5所示的應力云圖[5]。

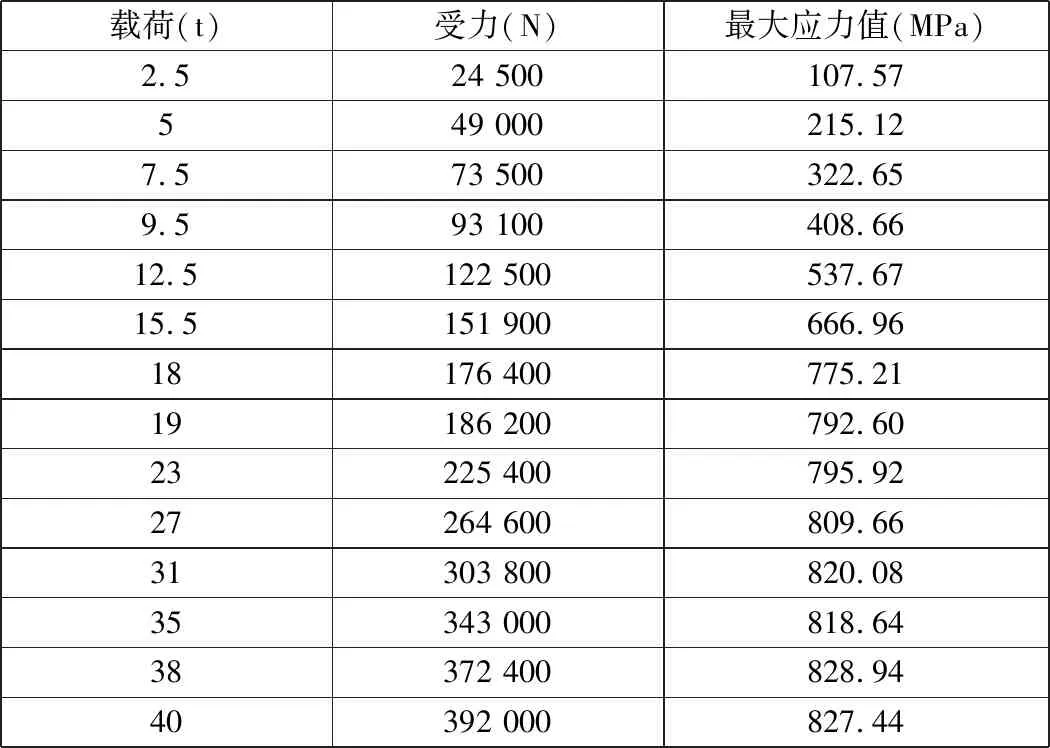
表2 仿真分析得到的卸扣最大應力

圖5 施加載荷9.5 t時卸扣本體最大應力云圖

從圖5中可知，當受力面上施加93 100 N的力時，卸扣本體最大應力為408.66 MPa。

4 公式計算

圖6為D型卸扣尺寸圖。《吊裝工藝計算近似公式及應用》中對D型卸扣本體的應力公式推導為：將卸扣本體視為鏈環的一半，按曲梁彎曲公式計算，并考慮“強化系數”，則環曲線部分中點的應力計算公式為[6]：

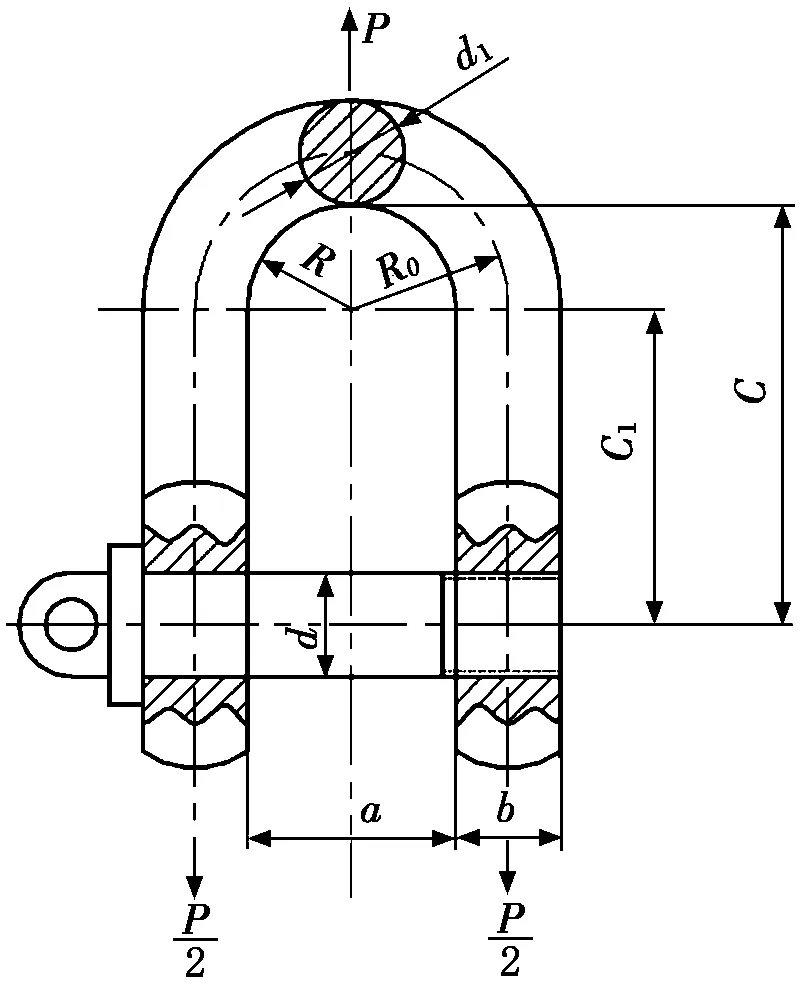
圖6 D形卸扣尺寸圖

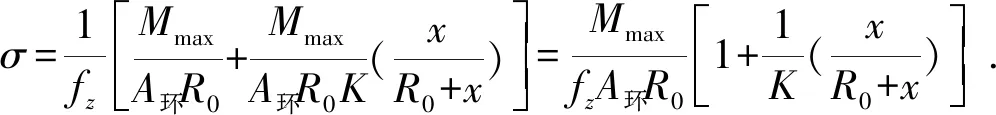
(1)

(2)

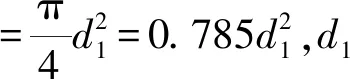
本文以巨力索具公司額定載荷為9.5 t的弓形卸扣為例進行計算，圖7為該弓形卸扣本體的具體尺寸圖。

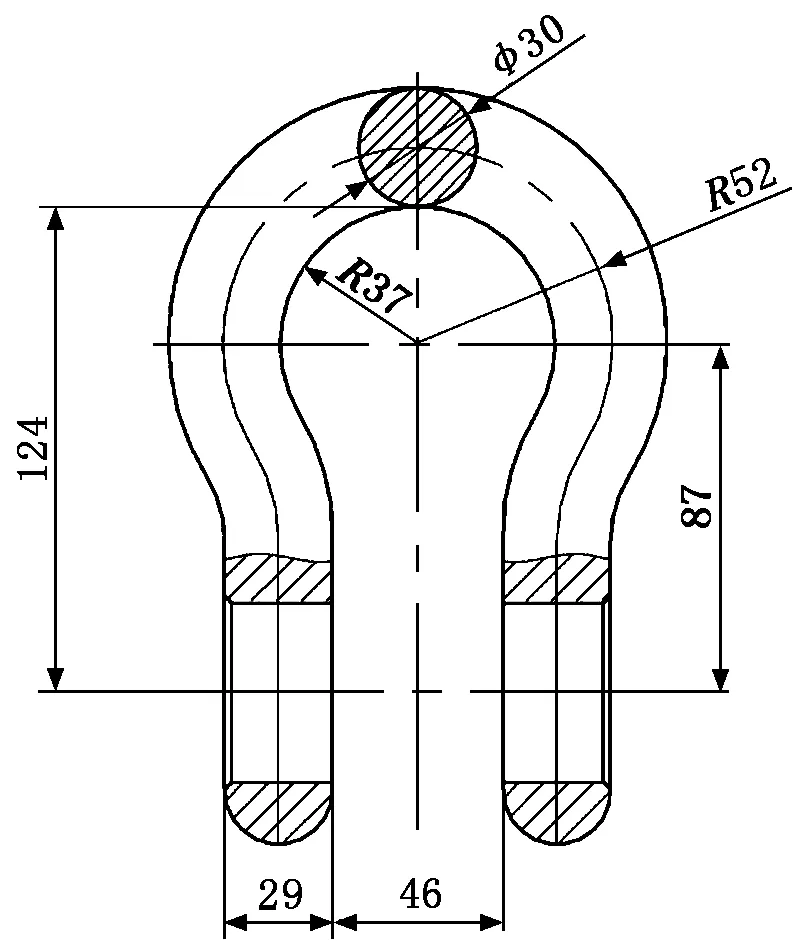
圖7 弓形卸扣尺寸圖

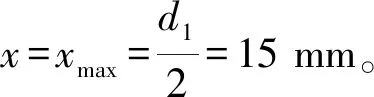
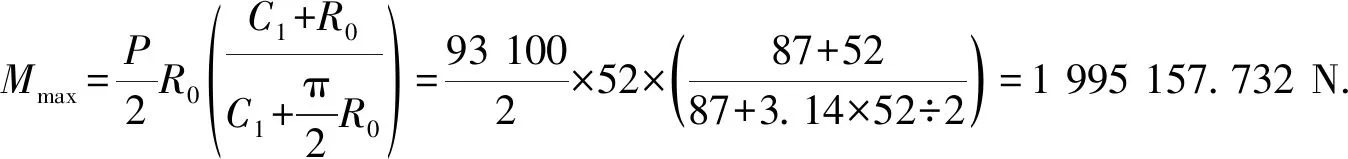
將其余的載荷分別進行計算，結果如表3所示。

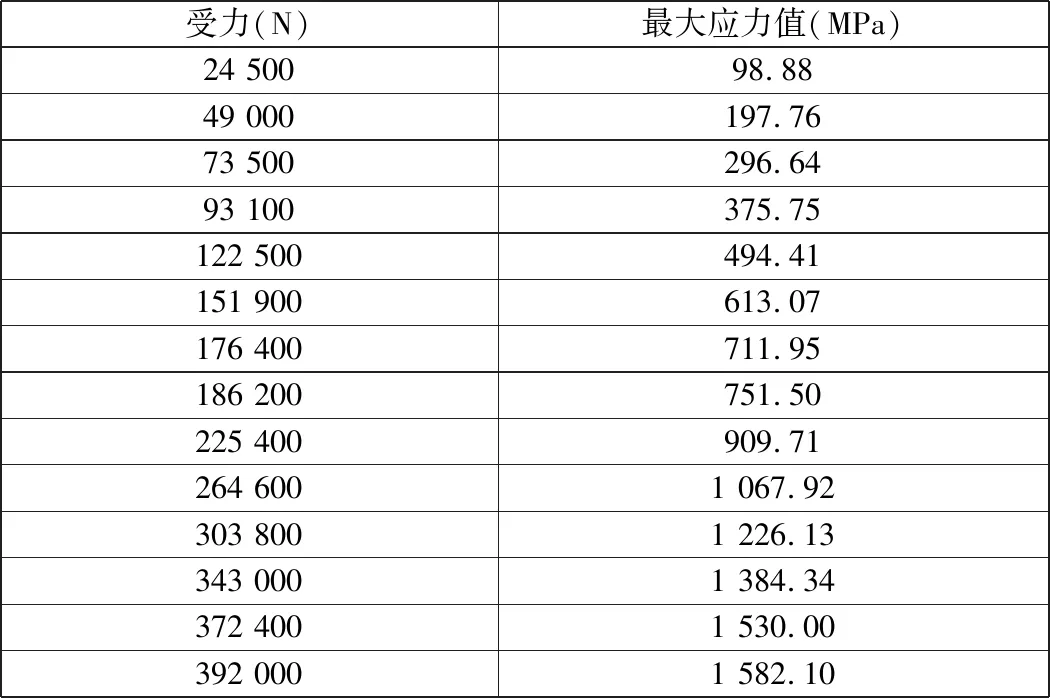
表3 公式計算得到的弓型卸扣最大應力匯總

5 結果對比與分析

不同受力情況下仿真和公式計算得到的弓形卸扣的最大應力數值匯總如表4所示。

將表4中數據轉換成折線圖可以更加清晰直觀地顯示兩組數據的相同和差異，卸扣本體最大應力數值對比，如圖8所示。

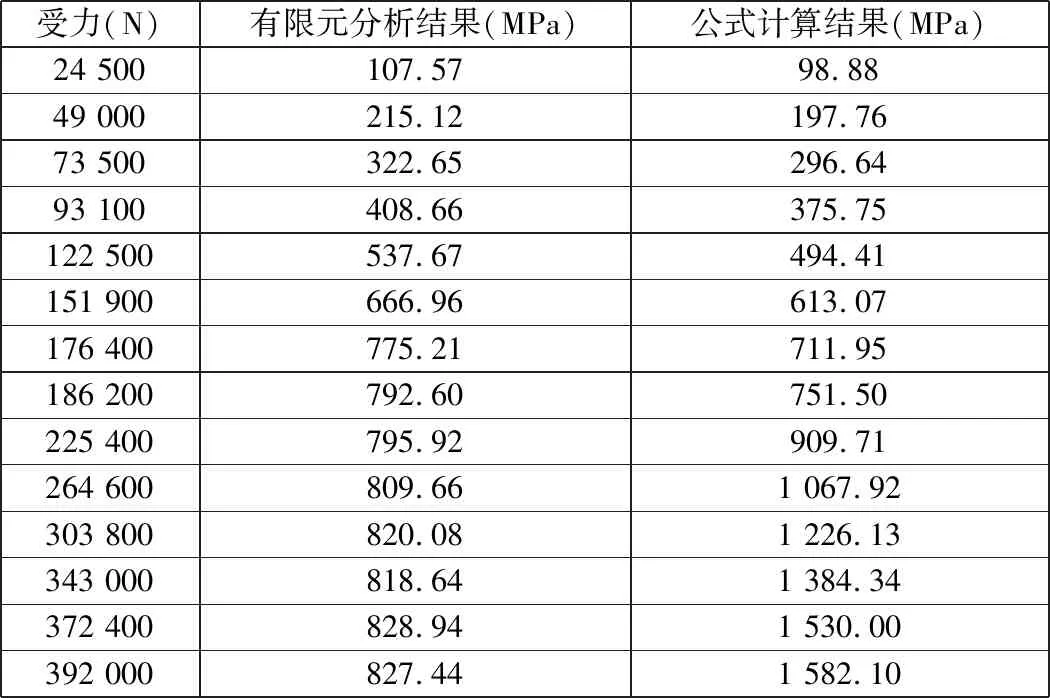
表4 仿真和公式計算得到的弓型卸扣最大應力匯總

由圖8可以看出：公式計算得到的卸扣本體的最大應力和有限元分析得到的卸扣本體最大應力在卸扣本體受力186 200 N之前結果相似，有限元分析得到的結果略大一些，兩者最大誤差約為8.1%；在受力186 200 N之后差別較大。分析原因為卸扣本體所用材料為34CrNiMo6，其屈服強度為760 MPa，當卸扣本體受力大于186 200 N的時候，卸扣本體發生塑形變形，此時材料進入屈服階段，當受力逐漸加大時，其應力變化較為平緩，但是對于公式來說，公式內沒有考慮材料的影響因素，所以在圖8中卸扣本體最大應力總體呈現線性上升的趨勢，沒有因為材料到達屈服強度而變化。

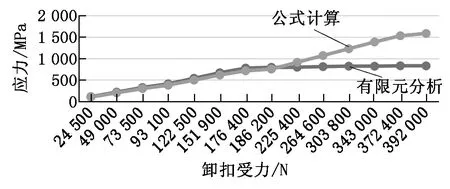
圖8 卸扣本體最大應力數值對比圖

6 結論

通過對計算結果和有限元分析結果對比分析可以得到結論：當卸扣本體最大應力小于制造卸扣材料的屈服強度的時候，蔡裕民在《吊裝工藝計算近似公式及應用》中提出的計算D形卸扣最大應力的計算公式也可以用來計算相同額定載荷的弓形卸扣本體的最大應力值。這個結論可以用于弓形卸扣的設計計算和對不明噸位的弓形卸扣進行核算，以此來滿足相關的工程吊裝要求。