高中物理電源輸出功率最大的條件論證及應用技巧

孫萬兵

(甘肅環縣第五中學)

在閉合電路中，電源提供的功率等于內外電路消耗的功率之和，對于含有可變電阻的純電阻電路，可變電阻的阻值變化直接影響著電源的總功率，也影響著閉合電路中各部分的功率分配.電源的最大輸出功率是電源性能的重要標志之一，求電源輸出功率最大值的問題也是電功率這部分內容的難點，學生雖經反復練習，但仍不得其法.筆者經過調查得知，學生出錯的根本原因在于不理解功率取最大值的條件.本文就電源輸出功率最大的條件論證及應用，結合筆者自己的經驗談一些粗淺的認識，供參考.

1 基本規律及條件論證

1)當電源電動勢E和內阻r一定，外電路的電阻R可變時，電源的輸出功率在滿足條件R＝r的情況下，可取得最大值.下面用多種方法對此結論加以證明，希望讀者從中選擇適合自己認識的證法，以加深對電源輸出功率最大條件的理解.

證明1公式法

電源的輸出功率，即消耗在外電路電阻上的功率P＝I2R，據閉合電路的歐姆定律有，所以

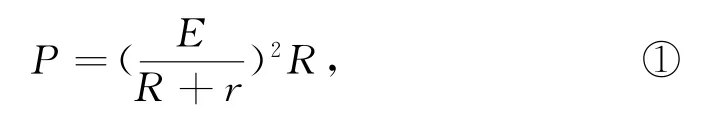
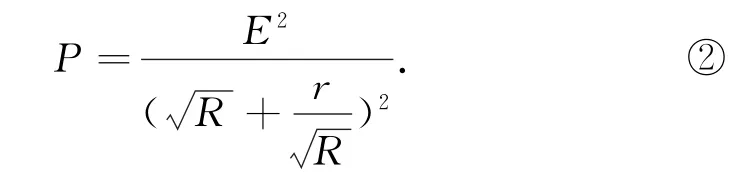
根據公式“若a、b均為正數，則，當且僅當a＝b時，a＋b取最小值，為，可得式②分母中，當(即R＝r)時，取最小值，為，因而，當R＝r時電源的輸出功率有最大值，為.

證明2解析法

將式①變形為

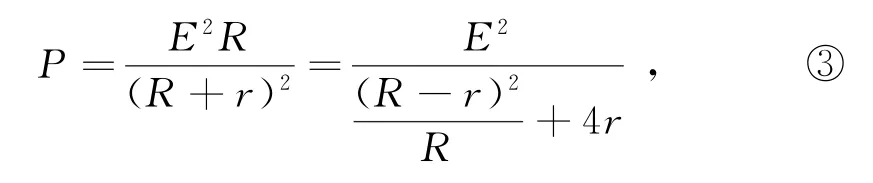
當式③分母中(R－r)2＝0(即R＝r)時，分母取最小值4r，此時電源有最大輸出功率

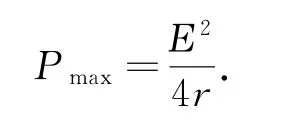
證明3利用二次函數的極值

若路端電壓為U，電路中電流為I，則外電路中消耗的功率應為P＝UI，而據閉合電路的歐姆定律有

所以電源輸出功率可以表示為

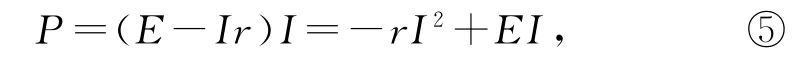
由式⑤可以看出，輸出功率P是電流I的二次函數，且二次項系數為負，因而當電流(此時R＝r)時，電源輸出功率有最大值，即

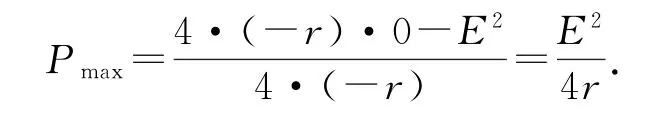
證明4圖像法

根據式④作出路端電壓隨電路中電流變化的圖像(如圖1)，圖像上任意一點N所對應的路端電壓為U，電流為I，則這時消耗在外電路上的功率P＝UI可以用圖中矩形(畫斜線部分)的面積來表示.

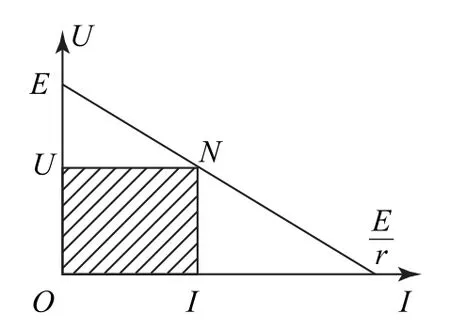
圖1

從圖中可以看出，當電路中電流很小或者很大時，圖中矩形的面積均較小，而只有當時，即時，矩形面積最大，即電源的輸出功率最大值.

證明5利用導數求極值

式①中P對R求導數可得

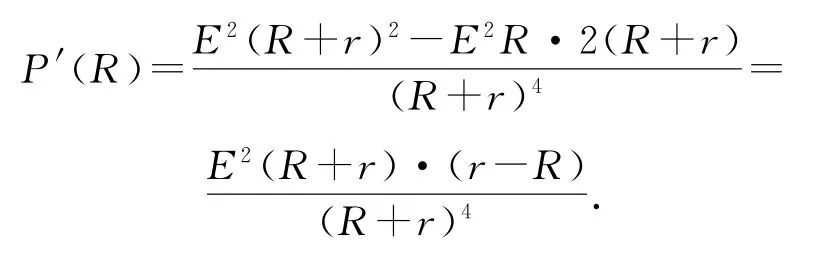
令P′(R)＝0可得，R＝r(R＝－r無意義，舍去)時，輸出功率有極值.

2)當電源電動勢E和外電路電阻R一定，而電源內阻r可變時，由式①可得，r取值越小，輸出功率P越大.

2 應用舉例

在實際應用中，有些問題是求電源向整個外電路輸出的最大功率，這類問題可以直接應用上述規律1)求解;有些問題是求外電路某一電阻或某一部分電路的最大功率，這類問題處理的常用方法是把求解對象等效看作外電路，而把其余電阻均等效看作電源內阻的一部分，當可變電阻包含在等效外電路中時，應用規律1)求解，當可變電阻包含在等效內電路中時，應用規律2)求解.

例1如圖2所示，定值電阻R1＝2Ω，R2為最大阻值為6Ω 的滑動變阻器，電源電動勢E＝12V，電源內阻r＝3Ω.求:

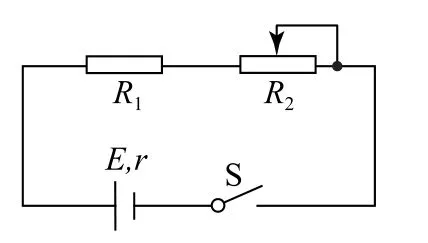
圖2

(1)R1和R2消耗的總功率的最大值.

(2)R1消耗功率的最大值.

(3)R2消耗功率的最大值.

(1)R1和R2消耗的總功率就是電源的輸出功率，若R1和R2的總電阻為R，則當R＝r＝3Ω(此時R2＝1Ω)時，R1和R2消耗的功率有最大值，最大值為

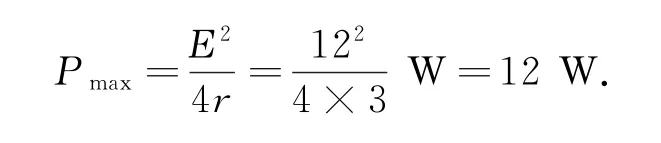
(2)把R1單獨看作外電路，而把R2等效看作電源內阻的一部分，此時等效電源內阻r1是可變的，且r1＝r＋R2，當R2＝0時，r1取值最小為r，此時R1的功率最大，為

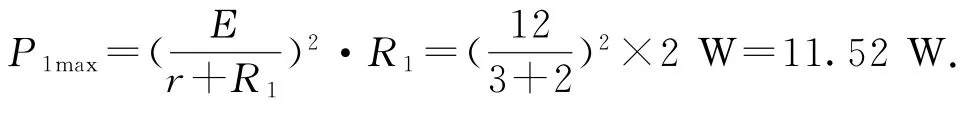
(3)把R2單獨看作外電路，而把R1等效看作電源內阻的一部分，此時的等效電源內阻r2＝r＋R1＝5Ω，因而當R2＝r2＝5Ω 時，R2的功率有最大值，為

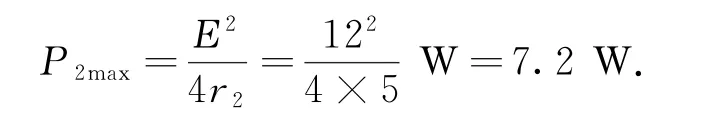
當求解最大功率的對象是可變電阻(或包含可變電阻)時，如果求解對象的總電阻變化到極限值還未能達到電源內阻(或等效電源內阻)，則求解對象的總電阻取最接近電源內阻(或等效電源內阻)的值時，其功率取得最大值.

例2如圖3所示，電源電動勢恒為12V，電源內阻r＝3Ω，定值電阻R1＝6Ω，R3＝15Ω，R2為一滑動變阻器，最大阻值為6Ω.求:

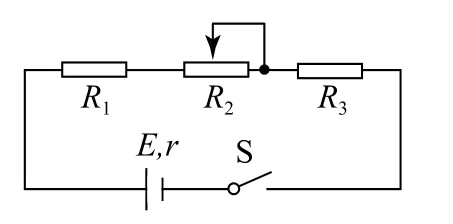
圖3

(1)R1和R2消耗功率的最大值.

(2)R2和R3消耗功率的最大值.

(1)把R1和R2看作外電路，則等效外電阻R外1＝R1＋R2.把R3等效看作電源內阻的一部分，這時等效電源內阻r1＝r＋R3＝18Ω，R外1阻值的變化范圍是6Ω≤R外1≤12Ω，當R2＝6Ω 時，R外1＝12Ω，R外1最接近r1，此時，R1和R2消耗功率有最大值，即

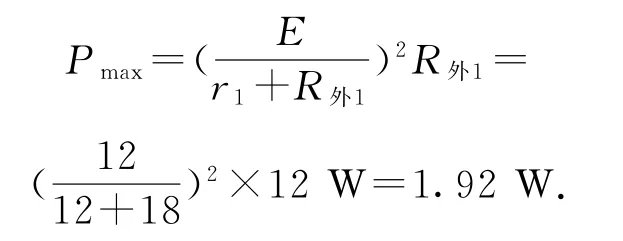
(2)同理，R外2＝R2＋R3，其變化范圍是15Ω≤R外2≤21 Ω，r2＝r＋R1＝9 Ω，因而當R2＝0時，R外2＝15Ω，R外2最接近r2，所以R2和R3消耗功率最大值

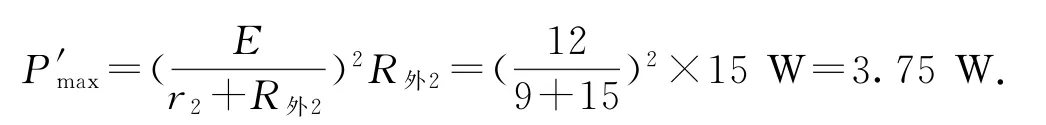
(完)