基于SPH-FEM方法的直升機典型金屬結構入水沖擊分析

簡成文 吳遠飛

（中國直升機設計研究所，江西 景德鎮 333001）

0 引言

飛機在高空高速飛行，當遇到緊急情況時必須迫降。飛機的迫降形式主要有3 種：場內迫降、場外迫降和水面迫降。其中，水面迫降是指著陸場在海洋、湖泊以及河流等水面上，水面迫降要求盡可能地靠近陸地，主要采用3 種方法（試驗法、解析法以及數值仿真法）對飛機水上迫降性能進行研究。20 世紀80 年代以前，研究人員主要通過動力相似縮比模型試驗來研究飛機的水上迫降性能。然而，隨著計算機科學技術的發展，飛機的全機模擬仿真以其精度高、成本低以及效率高的優點逐漸取代了試驗的研究方法。Anghileri M 等[1]對近似剛體結構進行入水試驗，并用SPH 方法進行仿真，對無量綱的加速度和壓力結果進行對比，數據吻合度較高。金屬板結構是直升機結構中最常見的結構，對直升機典型金屬板結構入水沖擊響應進行研究，可以為后續直升機整機入水仿真分析奠定基礎。該文采用SPH-FEM 流固耦合計算方法對金屬板結構入水沖擊響應進行研究。

1 SPH-FEM 流固耦合計算方法

SPH粒子與有限單元通過定義接觸的方式進行流固耦合計算。將有限單元的節點視為背景粒子，背景粒子的變量與相應的有限單元節點一致，例如粒子質量、位置、速度和應力等[2-3]。背景粒子只能被其他SPH 粒子搜索，在每個時間步內，接觸部分的相關信息會從背景粒子傳遞到有限元數據中。對有限元部分來說，這種傳遞相當于施加邊界條件，對SPH 部分來說，有限單元節點轉化為鄰近粒子，從而避免了邊界影響，進而使SPH 粒子與有限元之間具有很好的連續性。

位于有限元節點支持域內的SPH 粒子會對該節點產生接觸力，同時位于SPH 粒子支持域內的有限元節點會對該粒子產生接觸力，接觸勢能如公式（1）所示。式中：NCONT為粒子i的鄰近粒子數；m為粒子質量；ρ為密度；K為接觸罰剛度；rij為粒子間距；W為光滑函數（當xA、xB屬于相同個體時，W（xA-xB）=0）；?pavg為粒子間光滑長度的平均值；n為粒子總數；x為粒子位置。

接觸力如公式（2）所示。

式中：?為拉普拉斯算子。

對SPH 粒子來說，是將接觸力施加到動量方程的，如公式（3）所示。

式中：ν為粒子的速度矢量；t為時間；N為粒子數量；σ為應力；∏ij為人工黏度項；x為密度、速度和能量等變量；α、β為常數，取值分別為0.04 和0.01；xi是粒子i的位置。

在SPH 方法中，Monoghan 型的人工黏性將動能轉換為熱能，同時防止粒子相互接近時出現非物理穿透現象，如公式（4）所示。

式中：c為聲速；?為粒子的形函數。

對大多數流體仿真來說，常數α∏和β∏的取值分別為0.04 和0.01。

對有限單元來說，接觸力被當作外力施加到動力學方程，如公式（5）所示。

式中：、和u分別為加速度、速度和位移；M、C和K分別為系統的質量矩陣、阻尼矩陣和剛度矩陣。

SPH-FEM 流固耦合計算步驟如圖1 所示。

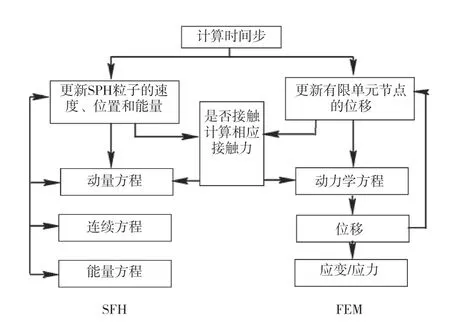
圖1 SPH-FEM 流固耦合方法計算示意圖

2 金屬板入水沖擊動力學建模

2.1 SPH 水體模型

水體單元模擬采用Langrange實體單元和SPH粒子單元，當采用實體單元時，將實體單元賦予水動力（Hydrodynamic）材料，狀態方程采用多項式狀態方程，如公式（6）、公式（7）所示。

式中：Ci為材料常數；μ為無量綱參數；Ei為內能；ρ0為水體的初始密度；ρ為當前水體的密度。

當水體采用SPH 粒子單元時，將SPH 粒子單元賦予Monaghan 狀態方程材料，狀態方程如公式（8）所示。

式中：p0為水體的初始壓強；ρ0為水體的初始密度；γ為常量，一般來說γ=7；B為狀態方程中的系數。

當流體最大流速為vmax時，狀態方程中的系數B如公式（9）所示。

考慮試驗水池足夠大，不考慮水池大小對仿真分析結果的影響，建立1 200 mm×1 200 mm×405 mm 的水域，水域由SPH粒子和實體單元耦合而成。其中，試驗件與水體接觸部分采用SPH 粒子模擬，該部分水域尺寸為800 mm×800 mm×100 mm，其余水域采用實體單元模擬。SPH粒子單元采用立方體形式，粒子間距為15 mm。

2.2 流固耦合接觸模型

SPH 粒子與FEM 單元之間的流固耦合通過接觸來設置。接觸是邊界條件高度非線性的復雜問題，需要追蹤接觸前物體的運動以及接觸后物體之間的相互作用。在接觸過程中，載荷隨時間、結構的變形而變化，即結構與載荷互相耦合。

接觸計算采用罰函數法，在每個時間步先檢查從節點是否穿透主面，如果無穿透，就不做處理；如果穿透，就在該從節點與被穿透主面之間引入一個接觸力，其大小與穿透深度、主面剛度成正比，從節點i受到的接觸力Fi如公式（10）所示。

式中：SLFACM為接觸剛度縮放因子；STF（SNODE）為主/從節點的接觸剛度；gi為穿透厚度。

同時，非線性懲罰方式能夠增加罰剛度，從而避免完全穿透。非線性罰剛度如公式（11）所示。

式中：ki為線性剛度；FSVNL為非線性剛度參數；Hcont為接觸厚度；為非線性罰剛度。

其接觸力如公式（12）所示。

該文對結構與水體之間的接觸進行設置，定義SPH 粒子為從節點，結構為主面，建立相應的接觸模型。

2.3 金屬材料模型

在大變形狀態下，金屬材料結構的薄弱區域將出現應力集中的現象，當應力過大并超過材料彈性極限時，薄弱區域的材料將進入塑性狀態，線彈性的本構關系不再適用，需要滿足相應的屈服準則。而屈服準則是在外部載荷作用下，物體內某一點開始產生塑性變形時應力所必須滿足的條件。

金屬材料屬于各向同性材料，該文中金屬的強度準則采用最大線應變準則，定義如下：當材料最大線應變ε1（或|ε3|）達到極限值時，材料發生破壞。其表達式如公式（13）所示。

式中：εT、εC分別為材料拉伸、壓縮時的極限應變。

在仿真計算中，當殼單元應變達到預期最大應變值時單元失效并刪除單元。

2.4 結構有限元模型

對元組件進行簡化，抽取相應的框架及面板中面，對結構焊接部分進行共節點處理，對底部試驗件的螺栓連接建立相應的彈簧元。為了模擬在吊籃頂部施加質量塊，建立相應的剛體約束，并在剛體中心點施加質量點。試驗件及組件采用四邊形殼單元模擬，單元尺寸為10 mm×10 mm。

試驗裝置結構如圖2 所示，有限元模型如圖3 所示。

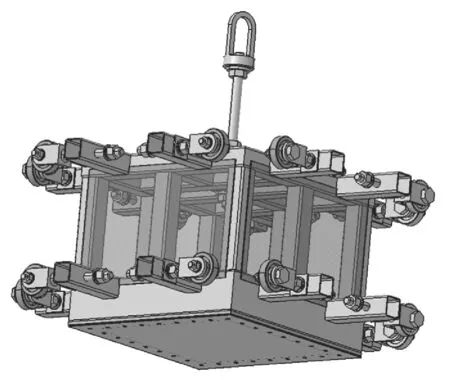
圖2 試驗裝置結構圖

圖3 有限元模型

3 金屬板入水沖擊試驗

3.1 試驗條件

試驗裝置由水池、試驗件、吊籃、導軌、臺架以及釋放裝置組成。試驗件安裝在吊籃底部，試驗件上布置應變片。吊繩與吊籃相連，通過起吊裝置及其控制系統調整吊籃的起吊和投放高度，吊籃頂部安裝快速釋放裝置，通過相應的控制系統實現快速投放吊籃和試驗件的功能。在水池與起吊裝置之間設置導軌，吊籃與導軌接觸處采用輪子設計，吊籃投放后將沿導軌下墜，從而控制試驗件的入水姿態。

吊籃具備可以承受垂向著水沖擊載荷及側向載荷的能力，吊籃上設置有配重安裝點，通過設置配重質量及配重位置得到試驗件不同質量狀態下的試驗條件。

吊籃四周布置加速度傳感器，試驗件從規定高度下落，以相應速度墜入下方水池。

3.2 試驗參數

金屬平板為0.8 mm鋁合金薄板，尺寸為400 mm×400 mm。結構總質量為50 kg，入水速度為2 m/s。在距薄板中心r=50 mm 處布置應變片，吊籃處布置加速度傳感器。

3.3 結果分析

典型金屬結構著水后的加速度響應、應變響應如圖4、圖5 所示。由圖4 可知，金屬平板入水大約5 ms 后，加速度與應變達到峰值，隨后迅速衰減，并在零點附近做周期振蕩。且加速度響應和應變響應的仿真曲線均與試驗曲線基本保持一致。結果表明，采用SPH-FEM 法進行金屬板入水沖擊分析可以真實地反映結構的沖擊響應特性。

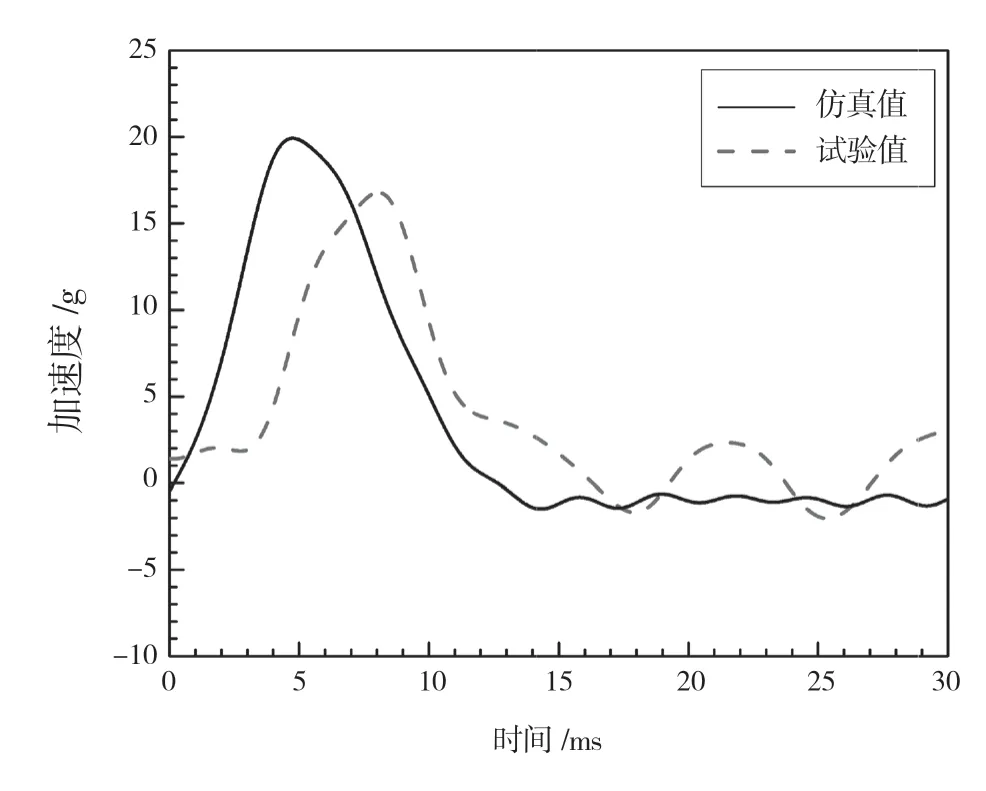
圖4 典型金屬結構加速度響應

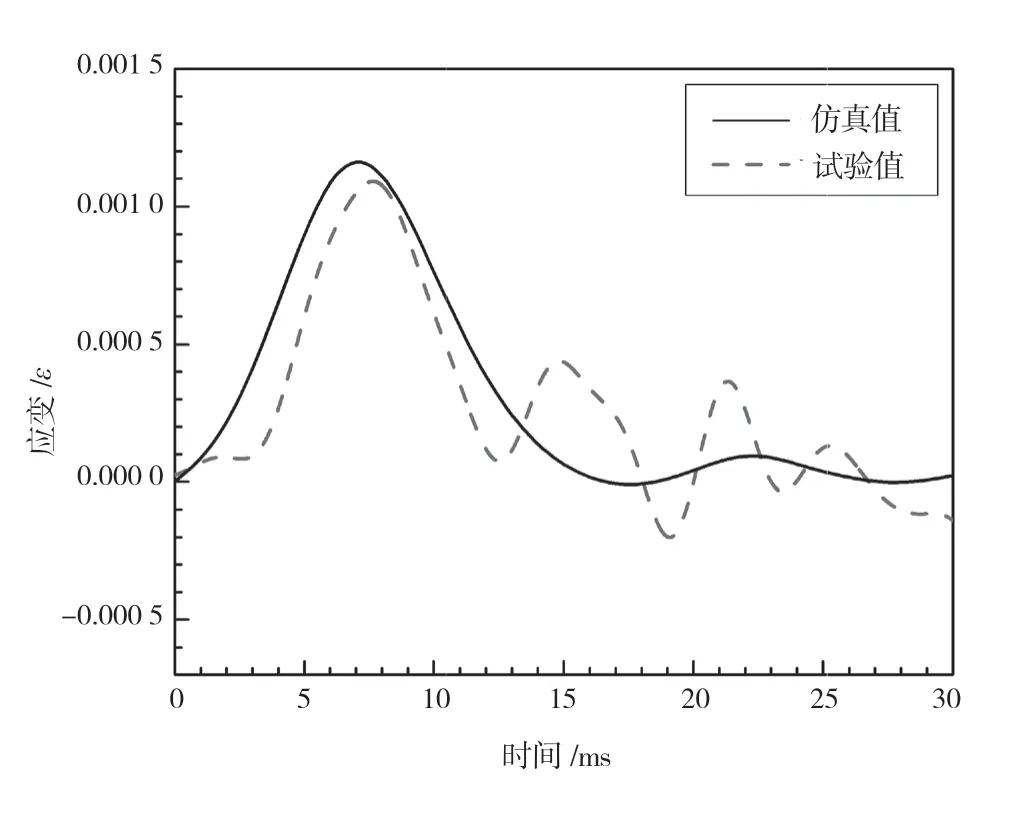
圖5 典型金屬結構距平板中心r=50 mm 處的應變響應

由圖4 可知，金屬板加速度仿真值為17 g，試驗值為17 g，結果的誤差為0%。由圖5 可知，距薄板中心r=50 mm處應變仿真值為0.001 1 ε，試驗值為0.001 15 ε，結果的誤差為5%。上述數據表明，該文所用仿真模型可以準確地描述結構的沖擊響應特性。

4 結語

該文建立了金屬板及其支撐結構、水體以及空氣的有限元模型，采用SPH-FEM 流固耦合方法對直升機典型金屬結構進行入水仿真分析，相關結論如下：1）結構加速度仿真值及應變仿真值與試驗值相比，誤差小于或等于5%，表明該文所用仿真方法具有較高的準確性。2）結構加速度與應變響應在結構入水沖擊初期達到最大，隨后迅速衰減，仿真曲線與試驗曲線變化趨勢一致。3）該文所用的仿真模型與仿真方法具有較好的可行性和較高的準確性，能夠為后續直升機整機入水仿真分析奠定基礎。