非靜止衛星星座地球站的等效全向輻射功率包絡計算方法

張曉燕

（國家無線電監測中心，北京 100037）

引 言

巨型低軌星座旨在通過解決數字鴻溝問題連接地球上暫無互聯網覆蓋的地區，為地球上的每個角落提供便捷、廉價、低延時、高帶寬的高速天基互聯網通信服務. 低軌互聯網星座系統的應用場景廣泛多樣，甚至可拓展至軍用領域，且巨型低軌星座可與地面互聯網、高空平臺等設施融合，構成天地一體融合通信網. 無論是哪種構型的星座系統，為了實現通信，完成組網，都離不開地球站(earth station, ES)至關重要的部署. ES一般由測控站、信關站、用戶站(固定、便攜和動中通)等組成，單星座系統的終端站數量甚至可以達到百萬級，理論上這些ES可分布在地球的任何地方. 例如，星鏈星座系統Starlink可支持約100萬座ES入網，均使用圓極化的極化方式，其中一期星座系統的測控站上下行鏈路使用Ku頻段，信關站上下行鏈路使用Ku和Ka頻段，用戶站上下行鏈路使用Ku頻段進行通信；二期星座系統增加用于測控站、信關站和用戶站的V頻段鏈路[1-3]. 如此多的ES投入使用，必然會對地位優先或其他已有的無線電系統尤其是同頻或鄰頻無線電臺(站)帶來額外的頻率干擾問題. 巨型低軌衛星星座系統的ES通常通過上行信號干擾其他無線電系統，下行信號對其他系統尤其是對靜止軌道(geo-stationary orbit,GSO)衛星星座系統的影響見文獻[4]中描述. 由此開展巨型低軌衛星星座系統的ES與其他無線電臺(站)間的干擾協調，以及對ES的最大輻射能量進行監管約束必不可少[5-6].

因此本文主要解決如何計算NGSO衛星星座系統ES上行鏈路到達GSO軌位弧的最大輻射能量—等效全向輻射功率(equivalent isotropically radiated power, EIRP)包絡問題. NGSO星座系統ES EIRP包絡通過一組最大EIRP值表格來定義，是從NGSO衛星ES產生的，到GSO軌位弧方向上離軸角的一個函數[7]. 不同緯度可能有不同的EIRP函數值表，與NGSO星座系統參數、干擾規避和減緩策略等息息相關. 即NGSO星座系統ES輻射的能量須包含在計算出的EIRP包絡內，能適應各種系統設計，且能達到減少不必要的協調和提高頻譜效率的目的.這就要求計算出的EIRP包絡越接近系統真實的工作值越好，且盡可能容納更多系統，從而提高頻譜的利用率. EIRP包絡計算方法參考文獻[8-10]等，衛星互聯網星座系統ES EIRP包絡的格式須滿足文獻[7]的定義和要求. 但文獻[7]中只給出了提交給國際電聯的EIRP包絡的格式要求和定義描述，并沒有給出計算EIRP包絡的具體方法，而是由用戶(衛星網絡資料所有者)根據各自系統的參數自行計算，暫無統一的計算方法. 因此本文旨在提出一種靈活通用的計算方法，支持監管應用. 經過國內外調研，兼顧我國空間業務的管理現狀，本文給出了滿足國際電聯要求的計算衛星星座系統ES上行EIRP包絡的詳細算法，流程如圖1所示.

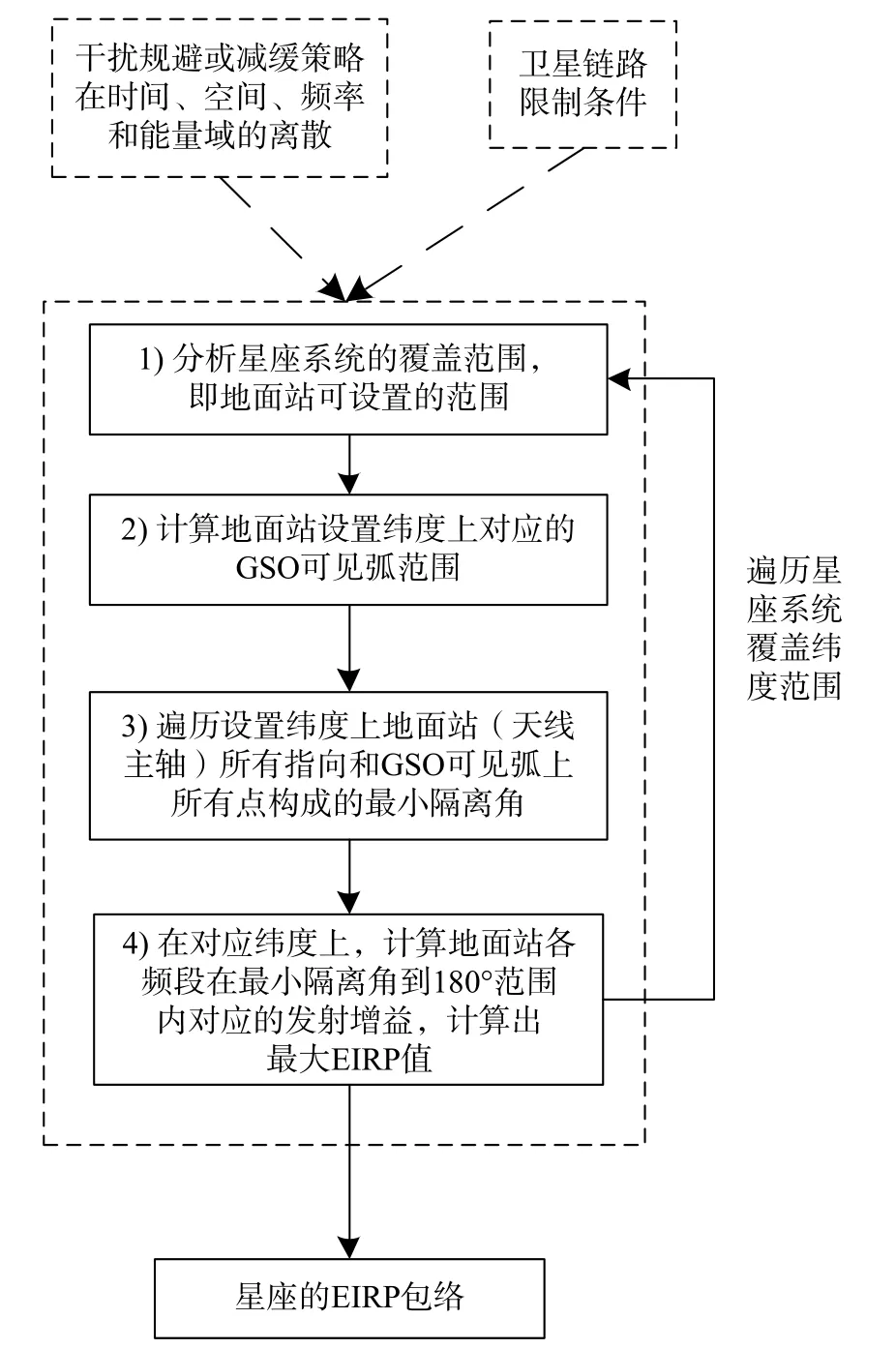
圖1 NGSO星座系統EIRP包絡計算框圖Fig. 1 Calculation block diagram of the EIRP mask in NGSO constellation system

框圖1的計算步驟如下：

1)根據輸入參數、干擾規避和減緩策略以及衛星建鏈的限制條件，計算衛星星座系統ES可設置范圍. 詳見1.1節.

2)在上述基礎上，計算ES設置緯度ELat,n及對應的GSO可見弧范圍，其中n為采樣點編號，n=1, 2, 3，… . 詳見1.2節.

3)在ES設置緯度ELat,n，遍歷ES所有指向和GSO可見弧采樣點ELon,k，計算出兩者之間的最小隔離角αmin. 其中k為GSO可見軌位弧采樣點編號，k=1，2，3，… .詳見1.3節.

4)[αmin,180°]內，根據ES各頻段的發射天線輻射方向圖，計算并找出ES各頻段的最大EIRP和對應的天線偏軸角αnk. 詳見1.4節和1.5節.

5)按照步驟1～4循環遍歷星座系統覆蓋范圍，計算覆蓋范圍內每個采樣緯度上ES各頻段的最大EIRP值，并得出星座系統的上行EIRP包絡—EIRP{(ELat,n, αmin,nk)}. 詳見第2節.

1 算 法

由于NGSO星座系統尤其衛星互聯網星座系統的軌道、波束、時間、頻率和功率等多維資源的動態性，要獲得NGSO星座系統ES的EIRP包絡，需遍歷ES最低工作仰角以上的所有指向，計算出ES指向與GSO可見弧的最小隔離角和ES輻射的最大可能EIRP值. 如圖2所示，ES所在經度不會對上述計算結果產生影響，因此為了計算方便可假設NGSO ES的經度為0°.

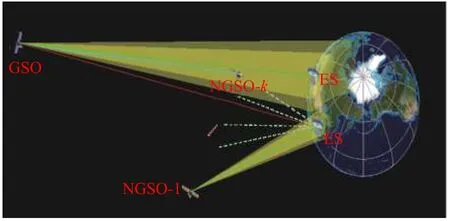
圖2 ES位置與EIRP包絡示意圖Fig. 2 Diagram of the ES location and the EIRP mask

通過遍歷ES設置緯度，按照下述步驟就可計算出該NGSO星座系統ES的EIRP包絡，但具有具體經緯度的衛星星座系統特定ES除外. 特定ES EIRP包絡的計算需在特定ES的對應位置遍歷其所有指向和GSO可見弧，計算出兩者間的最小隔離角，然后按照框圖1中的步驟4計算出此特定ES的最大EIRP和對應偏軸角. 通過遍歷星座系統的所有特定ES，計算出特定ES各頻段的EIRP包絡.

1.1 NGSO星座ES設置范圍建模

為了計算NGSO星座ES的EIRP包絡，需要對ES進行建模，包括國際電聯無線電通信部門(ITUR)公布的NGSO衛星ES參數、ES設置范圍、建鏈所受限制條件等.

ITU-R公布的NGSO衛星ES和NGSO系統工作參數，包括ES最大發射功率Pt、帶寬WB、ES天線尺寸D、天線輻射方向圖Gt(θ)和最大發射增益Gt、天線接收方向圖Gr(θ)和最大接收增益Gr、波束寬度φ、最低工作仰角ε0、接收系統噪聲溫度T和小區間距df、每平方千米同時同頻輻射能量的NGSO ES平均密度m、最小運行高度h0、禁區角度α0等.特定ES還包括站址地理坐標經緯度(PLon,k,PLat,k). 注意：不同緯度和方位角所對應的最低工作仰角可能不同，可通過最低工作仰角表{ε0(ELat,k，A)}列出，其中A為采樣緯度ELat,k最低工作仰角對應的方位角.

ES設置范圍由NGSO可達到的緯度范圍(由軌道傾角i確定，取值范圍為0≤i≤180°)、衛星的最大半視角φ0和最低工作仰角ε0等確定[11]，如圖3所示.

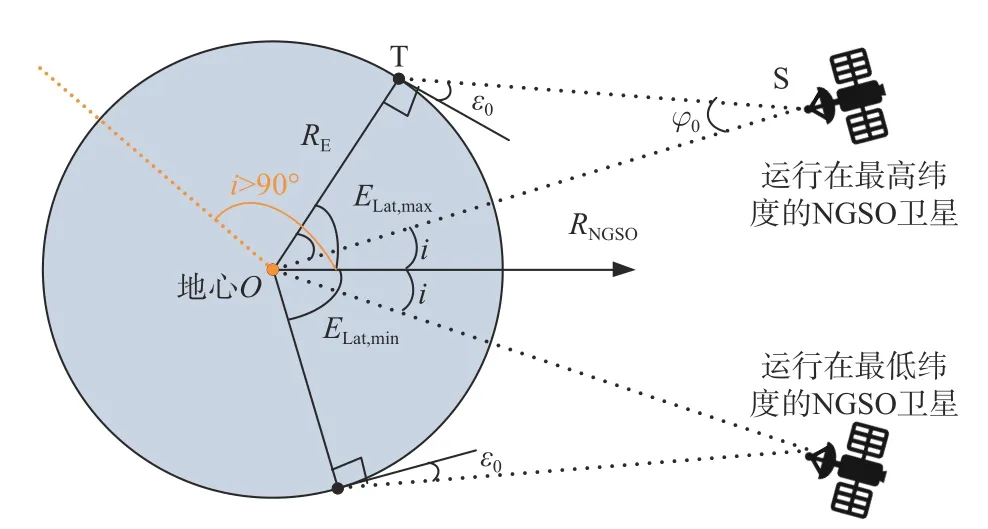
圖3 NGSO ES可設置緯度范圍示意圖Fig. 3 Diagram of the latitude range of the NGSO ES

從圖3中可知RNGSOsinφ0=REsin(π/2+ε0)，即：

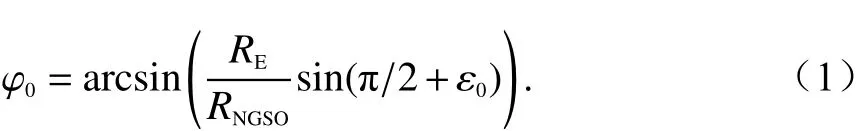
式中，RE= 6 378 km為地球半徑；為NGSO衛星到地心的距離，a=RE+(RA+RP)/2為NGSO衛星軌道的長半軸，e= (RA?RP)/(2a)為軌道偏心率，RA和RP分別為NGSO衛星的遠地點和近地點高度，可從ITU-R公布的NGSO衛星參數中獲取. 在ε0不變的情況下，要使ELat,max最大，需要使地心角∠TOS最大，即φ0最小. 由式(1)可知，當RNGSO取最大值時，φ0為最小值φ0,min，可得出NGSO ES設置的最高緯度；而RNGSO取最小值時，φ0為最大值φ0,max，可得出NGSO ES設置的最低緯度. 即NGSO ES可設置的最高緯度為

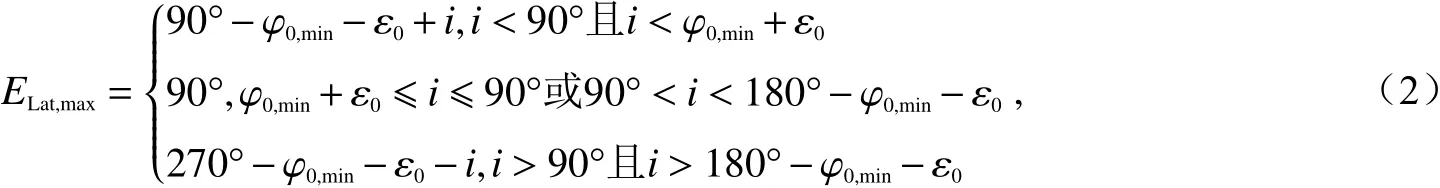
最低緯度為

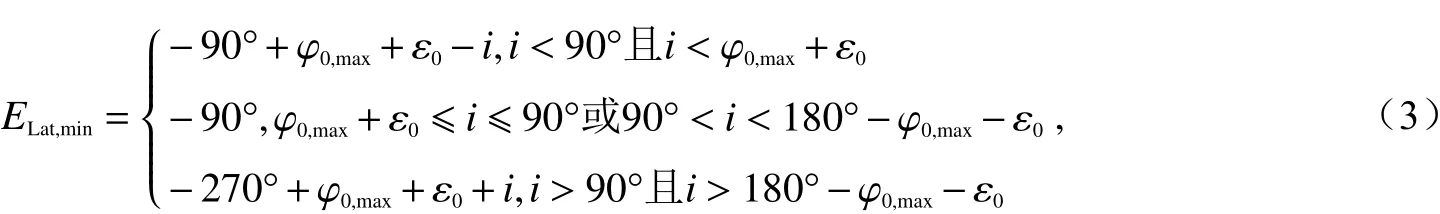
式中：若遠地點的星下點位于北半球，則

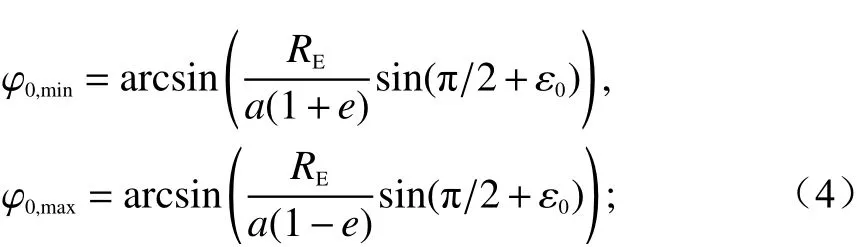
若遠地點的星下點位于南半球，則

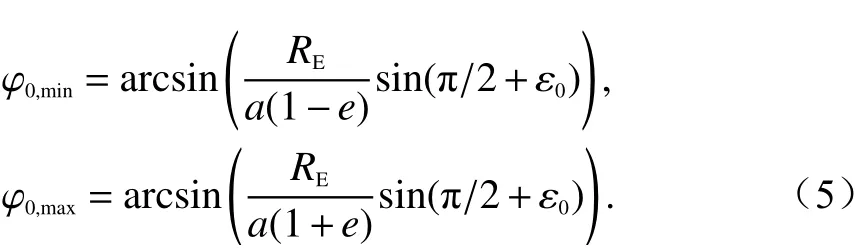
在ES可設置緯度范圍[ELat,min，ELat,max]內還需滿足建鏈限制條件，才能計算EIRP的有效上行鏈路.建鏈限制條件包含：1)NGSO衛星ES到GSO衛星的仰角至少不低于ε0(ε0≥5°)，也就是距離GSO衛星為的地球表面點為有效的NGSO ES計算點；2)NGSO ES須設置在GSO的禁區(?α0，α0)外；3)NGSO正常工作的距地高度不低于最小運行高度h0；4)為了得出干擾GSO的最差情況，若沒有給出明確的干擾規避或減緩策略，通常假設NGSO ES優先與離GSO軌位弧最近的NGSO建鏈. 若已知明確的干擾規避或減緩策略，將干擾規避和減緩策略轉化為明確的建鏈限制條件，如條件2和條件3就是較通用的干擾規避和減緩策略，其他干擾規避和減緩策略也可轉化為條件2和條件3.

1.2 ES可見GSO軌位弧

圖4為NGSO ES和GSO軌位弧幾何示意圖，NGSO ES的可見GSO軌位弧范圍為

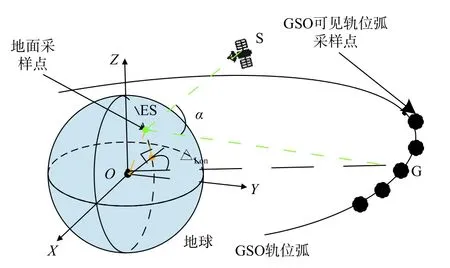
圖4 NGSO ES和GSO軌位弧幾何示意圖Fig. 4 Geometry of the separation angle between non-GSO ES and GSO arc

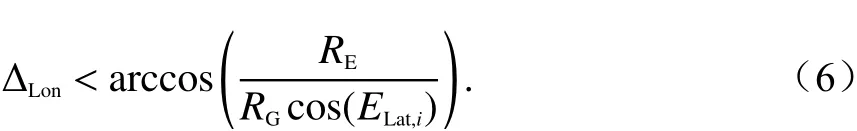
式中：△Lon=GLon?ELon，GLon和ELon分別為GSO可見軌位弧采樣點經度和NGSO ES的經度；RG= 42 162 km為GSO衛星軌道半徑；ELat,i為NGSO ES的采樣緯度.為計算方便可假設NGSO ES的經度ELon= 0°，則GSO可見軌位弧采樣點GLon,k=ELon+kΔstep，△step為可見軌位弧的采樣間隔.

1.3 最小隔離角

為更方便地計算出NGSO星座系統上行鏈路對GSO星座系統的影響，引入NGSO ES與GSO軌位弧間隔離角α(見圖4)，即NGSO衛星與GSO軌位弧在NGSO衛星ES處所形成的隔離角，也可看作是NGSO衛星ES天線與GSO衛星間的偏軸角. 偏軸角越小，說明NGSO衛星ES輻射到GSO衛星的能量越多，則GSO衛星上行鏈路更容易受到NGSO衛星ES的影響.

如圖4，對NGSO衛星ES可設置緯度范圍[ELat,min，ELat,max]采樣，計算對應的最小隔離角. 設ES的采樣緯度為ELat,n、天線指向方位角AE∈[0，360°)，仰角LE∈[ε0，90°]，到GSO可見軌位弧內任意采樣點的方位角和仰角分別為AG和LG. 根據余弦定理得出隔離角為

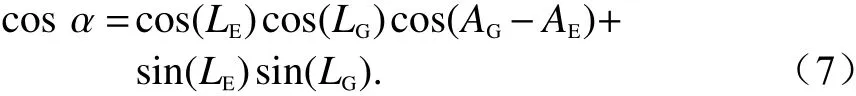
ES到GSO的方位角AG和仰角LG分別為[12-13]：

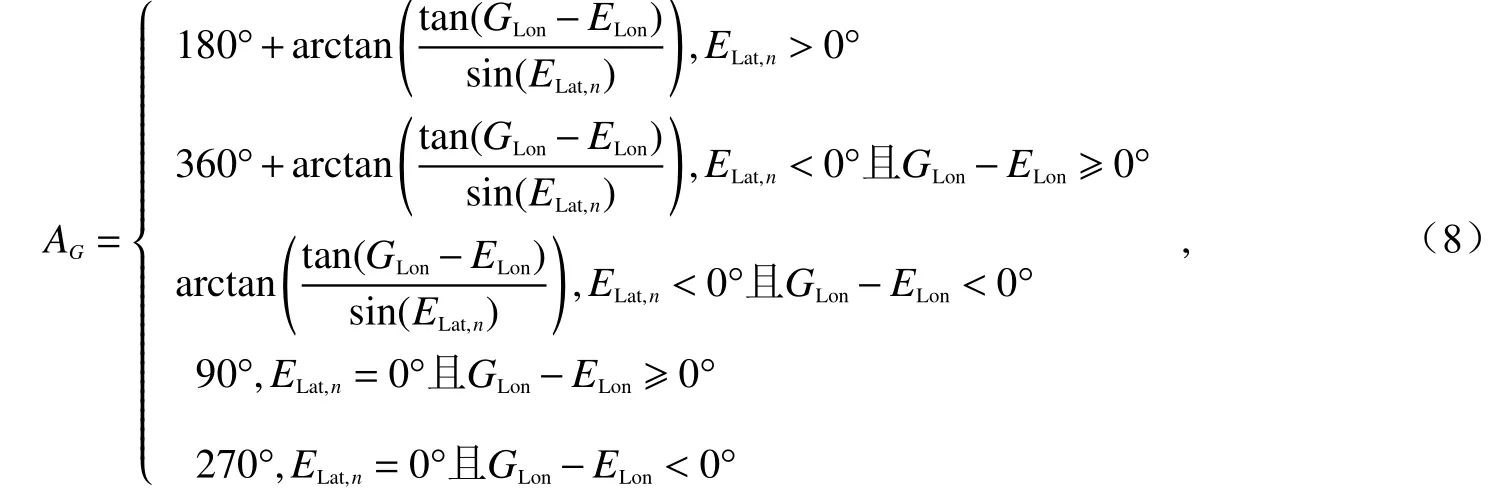
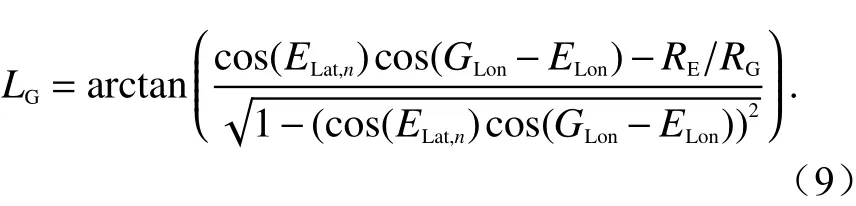
根據每個ES采樣緯度，由式(7)求出對應的最小隔離角αmin=min{α}. 若最小隔離角小于對應位置的GSO衛星禁區角，則相當于衛星ES在指向[αmin，α0)內不發射功率. 若要使用此位置處的衛星ES需調整天線的指向.

1.4 天線輻射方向圖

得出最小隔離角后，在ES天線偏軸角α∈[αmin,180°]內，根據ES各頻段的發射天線輻射方向圖，計算并找出各頻段的最大偏軸發射增益Gt(αn)=max{Gt(α)}及對應的天線偏軸角. 若αn小于GSO禁區角度α0，則αn=α0.

1.5 EIRP包絡

在采樣緯度ELat,n，NGSO星座ES到達GSO軌位弧采樣點GLon,j的最大EIRP為

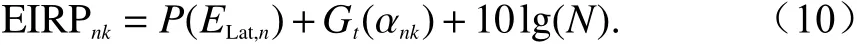
式中：EIRPnk為緯度ELat,n處NGSO星座ES某頻段輻射到GSO軌位弧GLon,k的最大EIRP，單位dB(W/WB,ref)，WB,ref為參考帶寬；P(ELat,n)為緯度ELat,n處NGSO星座ES某頻段輻射的最大功率，單位dBW；Gt(αnj)為緯度ELat,n處NGSO星座ES某頻段天線到GSO軌位弧GLon,k的最大發射增益，單位dBi；N為同時同頻輻射能量的NGSO ES數量，N=df2×m. EIRP包絡只需計算同時同頻輻射能量的NGSO衛星ES. 除了特定ES外，為了求出NGSO ES對GSO的最大影響，可認為同時同頻發射的N座NGSO ES位于同一點.

按照上述方法遍歷NGSO星座ES的可設置區域，計算每個采樣點的最大EIRP，得出該NGSO星座各頻段的EIRP包絡.

2 仿真計算

以衛星網絡資料3ECOM-1進行仿真計算，如圖5所示.

圖5 3ECOM-1衛星星座Fig. 5 Satellite constellation of 3ECOM-1

2.1 仿真參數

該衛星星座EIRP包絡的主要輸入參數如表1所示.

表1 仿真輸入參數Tab. 1 Simulation input parameters

2.2 仿真步驟

1)用仿真輸入參數根據1.1節構造出NGSO星座系統ES的設置和建鏈范圍.

2)遍歷ES設置范圍，針對每個采樣緯度ELat,n計算每個衛星ES輻射頻率組的EIRP值. 將頻率組中頻率重疊的最大EIRP值進行合并處理，即相同頻段的EIRP包絡值取不同頻率組中計算出的EIRP的最大值.

3)遍歷衛星網絡中每個接收頻率組，獲取當前頻率組的最低頻率及最高頻率，確定參考帶寬. 參考帶寬由《無線電規則》第22款相應頻段的限值參數確定[5].

4)計算覆蓋范圍每采樣緯度上、每個接收頻率組的最大EIRP值，其中緯度步進為1°.

①根據1.1節求解NGSO星座ES位置范圍.

②根據1.2節確定每個采樣緯度ELat,n對應的可見GSO軌位弧范圍△Lon和GSO可見軌位弧各采樣點GLon,k=ELon+kΔstep，其中△step= 180°×10?3/π.

③計算各采樣點的最小隔離角.

對設置范圍進行遍歷，得到一個點集：

將上述柵格化點集按照1.3節式(8)和(9)轉化為指向GSO軌位的仰角和方位角：

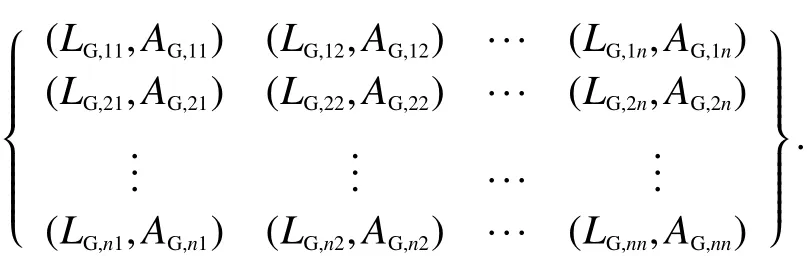
遍 歷 每 個 緯 度 采 樣 點 指 向AE∈[0，360°)和LE∈[ε0，90°]，再通過式(7)，計算出對應的最小隔離角：

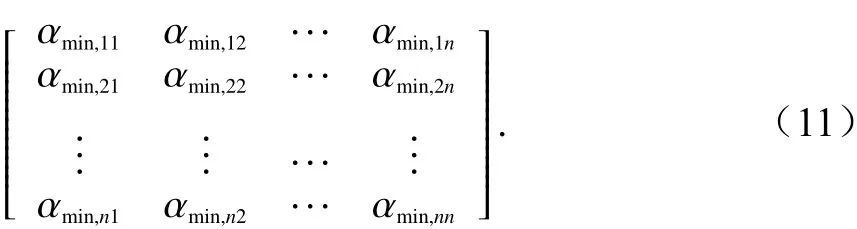
式中，αmin,nk為緯度采樣點ELat,n處到GSO可見軌位弧GLon,k的最小隔離角. 若最小隔離角小于對應位置的GSO衛星禁區角，則此位置處衛星ES天線的偏軸角最小為α0.

④計算各采樣點天線輻射增益.

根據1.4節ES各頻段的發射天線輻射方向圖和式(11)中各項，計算得出ES各頻段的最大旁瓣增益和對應的天線偏軸角：

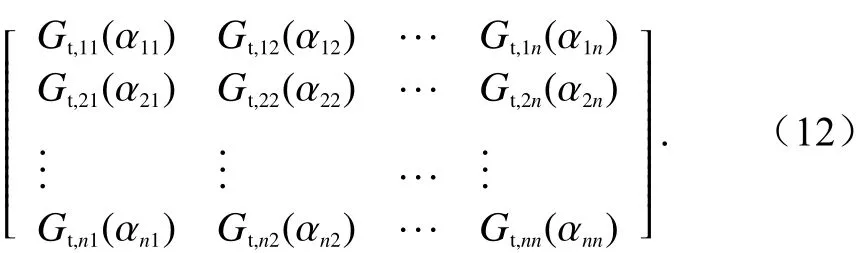
式中，每一行對應相同的采樣緯度和GSO可見軌位弧的不同采樣點.

⑤計算不同頻段的EIRP包絡.

按照1.5節計算每采樣點的最大EIRP. 首先，根據表1中的仿真參數得出各頻段的最大發射功率，結合式(12)，代入式(10)中計算出各緯度采樣點上不同隔離角和不同頻段的最大EIRP：

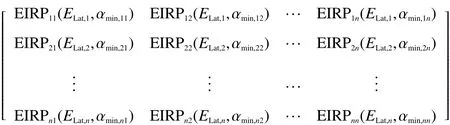
星座EIRP包絡的仿真結果見2.3節.

2.3 仿真結果

由上述仿真計算，可得出3ECOM-1衛星星座的EIRP包絡的仿真結果，見表2.

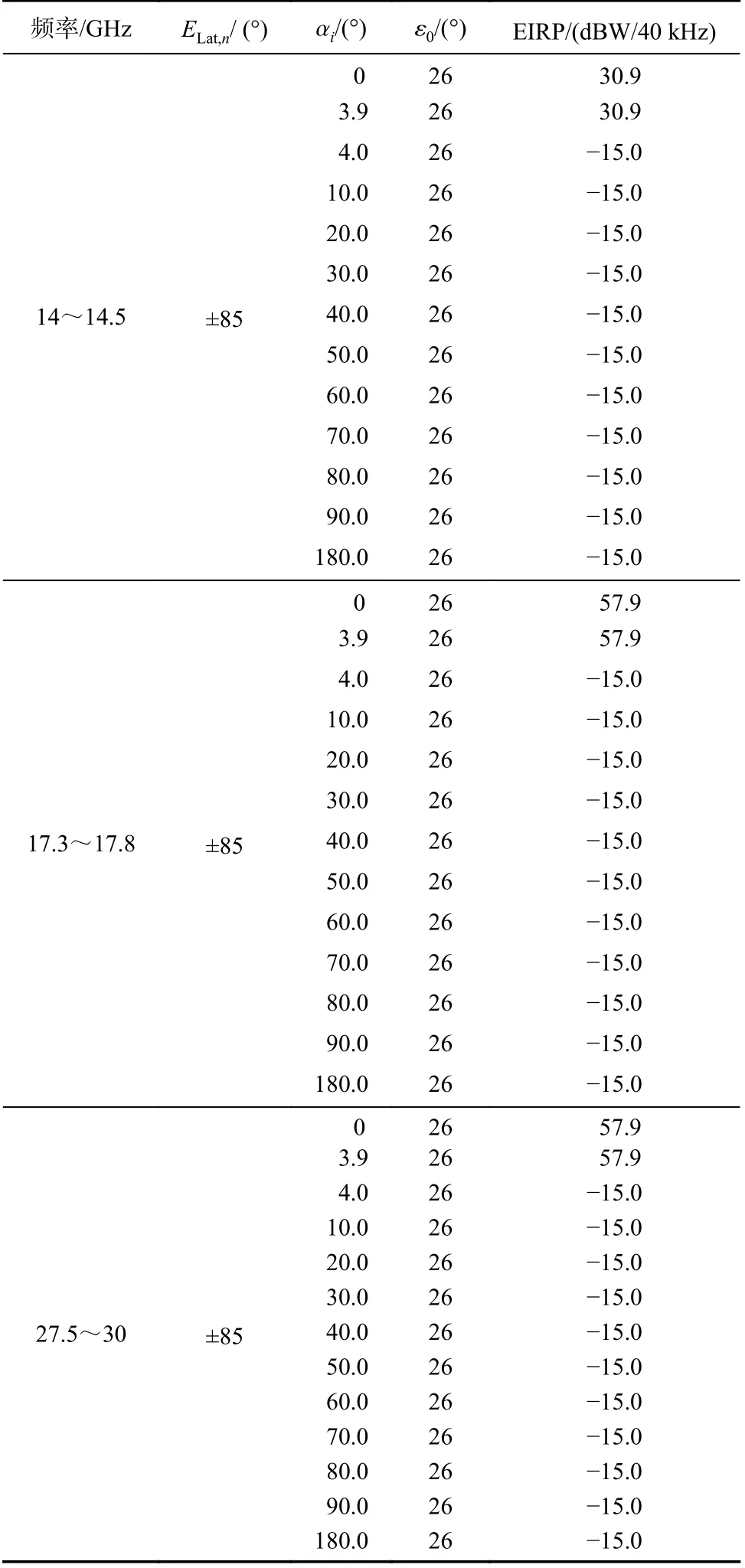
表2 續表

表2 3ECOM-1衛星星座EIRP包絡計算結果Tab. 2 The EIRP mask of 3ECOM-1 satellite constellation

由于無法得到真實的3ECOM-1衛星星座ES的詳細運行參數，尤其是相關的干擾減緩和規避策略等，本文的仿真結果僅依據國際電聯國際頻率信息周報(international frequency information circular,IFIC)第2 920期中的SRS數據庫(詳見仿真輸入參數表1)得出. 仿真結果可能會高于3ECOM-1衛星星座系統ES的實際EIRP包絡值，但本文的計算方法為一種靈活通用的方法，所要仿真系統的各項實際工作參數越詳細，代入本文算法后得到的仿真結果就會越接近真實值. 由于無法得知各衛星操作者提交給國際電聯的EIRP包絡在計算或仿真時使用的具體條件，或者說3ECOM-1衛星星座系統的詳細運行和操作參數，因此本文算法暫未找到可行的對比驗證對象.

3 結 論

文中提出了一種靈活通用的計算方法來支持計算NGSO網絡ES EIRP包絡用于實際監管計算. 為了使仿真結果更接近NGSO衛星星座系統上行鏈路的真實值，需要詳細了解所要仿真的各項系統參數，尤其是相關的干擾規避和減緩策略等. 本文計算出的EIRP包絡滿足國際電聯EIRP掩碼格式，可參與后續上行等效功率通量密度的計算，從而來判斷NGSO星座是否滿足國際電信聯盟《無線電規則》第22款的限值，并開展NGSO星座系統與其他無線電系統間的干擾協調和監管約束等.

本文通過推導NGSO系統的覆蓋范圍及對應GSO可見軌位弧數學表達式，明確了NGSO ES可設置范圍采樣點處最小隔離角的計算以及如何獲取相關的最大發射偏軸增益；確定ES可設置范圍柵格遍歷、發射天線偏軸增益及其EIRP包絡的仿真計算步驟，使EIRP包絡估計更精確且計算效率更高. 以本文為基礎，后續會開展NGSO星座上行鏈路等效功率通量密度的研究. 由于暫無法獲得有效的驗證對比對象，因此本文方法會在后續實際應用中進一步驗證或改進.