風力發電機塔筒晃動位移監測新方法

王 華，孟 歡，李 萍

（上海港灣工程質量檢測有限公司，上海 201315）

大型高聳建筑物的晃動位移測量方法總體可歸納為以下幾種方法：GPS(Global Positioning System)/北斗衛星測量法[1]、激光測量法[2]、傾角測量法[3]、視頻技術測量法[4]、低頻振動位移傳感器測量法[5]。這些測量方法都存在較明顯的缺陷。GPS/北斗衛星測量法的測量精度通常只有厘米級別、需要幾公里范圍內有靜態的基準參考點，不適合用于遠離海岸線幾十公里的海上風機塔上。激光測量法雖然精度可達到毫米級別，但是需要在被測對象附近找到靜態的設備安裝點、并且受天氣影響較大，也不適合用于海上風機塔的晃動位移的測量。傾角測量法是一種間接測量方法，在高聳建筑物的多個高程布置一定數量的監測點，然后通過數字積分模型得到位移曲線。傾角測量法安裝方便、不需要靜態參考點，但是由于傾角儀同時能感應到結構的水平向振動加速度信號，需要對其輸出信號進行低通濾波（通常濾波截止頻率要低于結構的1 階固有頻率值）后，方可使用，進而導致其無法測量結構的較高頻率水平向振動位移。因此，傾角測量法得到的位移為高聳建筑物的1階固有頻率以下的超低頻率位移。視頻技術測量法主要是通過高性能的攝像頭快速抓拍建筑物，然后通過圖像處理后得到建筑物的晃動位移。此方法適合用于實驗室的建筑物模型實驗，或者大型建筑物頂部附近有靜態參考點的場景。低頻振動位移傳感器不需要靜態參考點，使用非常方便，但是由于其下限頻率無法達到0，只能感應到其有效頻帶范圍內的各種周期性振動位移信號，不能得到大型高聳建筑物的非周期信振動位移信號和傳感器有效頻帶范圍外的周期性振動位移信號。

基于現有大型高聳建筑物的晃動位移測量方法都存在明顯的缺陷，晃動位移特性對于此類結構物動力響應的研究又極其重要[6–10]。本文提出了一種可用于海上風機塔晃動位移自動化監測的新方法：把傾角測量法和低頻振動位移傳感器測量法融合到一套同步采集系統，設計了一種信號擬合疊加數字模型，把兩種測量方法的兩條位移時程曲線同步疊加成一條位移時程曲線，精確得到海上風機塔的晃動位移時程曲線。本方法彌補了傾角測量法、低頻振動位移傳感器測量法的缺陷。模型實驗和實測信號分析結果表明此方法可得到0.1 毫米級別的晃動位移分辨率、可感應到0～10 Hz的晃動位移信號。

1 測量設備和原理介紹

本方法由2個高精度的雙向動態傾角儀、1臺高精度的多參數輸出傳感器、1臺8通道的高精度動態數據采集儀構成。其中多參量輸出傳感器含雙向動態傾斜度信號輸出、雙向低頻振動位移信號輸出，傳感器布置位置情況如表1所示。

表1 新方法的傳感器布置情況

雙向動態傾角儀為河北振創電子科技有限公司生產的QYG01-1 型動態傾角儀，其動態分辨率為0.001 度，低通濾波后的有效頻帶為0～0.1 Hz，量程為10度，模擬量信號輸出。多參量輸出傳感器為河北振創電子科技有限公司生產的QZDC-A 型傳感器，可同步輸出雙向動態傾斜度信號、雙向振動位移信號，其中動態傾斜信號的性能與QYG01-1型動態傾角儀一致，其低頻振動位移信號的分辨率為0.1 mm，有效頻帶為0.1 Hz～10 Hz，量程為2 m，模擬量信號輸出。高精度動態數據采集儀為河北振創電子科技有限公司生產的G01NET-3F型數據采集儀，其A/D位數為24位，8通道同步輸入，RJ45網口數據傳輸。系統配套河北振創的G01NETFDC風機基礎和塔筒安全監測軟件使用，可實現信號的自動化采集與在線分析。

海上風機塔可簡化為1個豎立的懸臂梁。由于風機塔的主要外部作用力為低頻率的風荷載、潮流荷載、葉片等效作用力荷載[11–13]，且其1 階固有頻率介于0.15 Hz～0.4 Hz[14]，所以其晃動位移信號的頻率成分主要集中在0～5 Hz 范圍內，可把海上風機塔的晃動位移信號分為0～0.1 Hz 和0.1 Hz～5 Hz兩個頻帶段。0～0.1 Hz 頻帶段的晃動位移信號通過傾角法測量；0.1 Hz～5 Hz 頻帶段的晃動位移信號通過低頻振動位移傳感器測量。

基于3個點的傾斜度計算塔筒頂部的位移的步驟可分為以下3個步驟：

第1步：基于某個時刻的3個點的傾斜值進行塔筒斜率曲線擬合。

假設f(x)為塔筒各位置的斜率曲線函數，且定義此函數為二次函數：

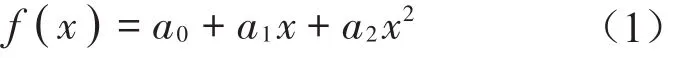
然后基于三個測點的實測斜率值對此函數進行最小二次方程求解得到其3個常量的值。

第2 步：對斜率曲線函數進行積分得到塔筒頂部的位移值。

假設塔筒高H米，其位移為S1，則：

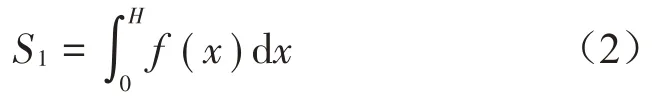
第3步：不斷循環重復以上兩步，得到某時間段的塔筒頂部位移數組：

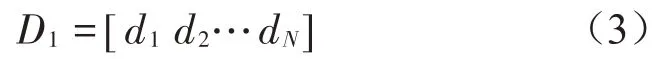
N為此時間段采集到的數據長度。

假設這段時間振動位移傳感器輸出的振動位移數組為：

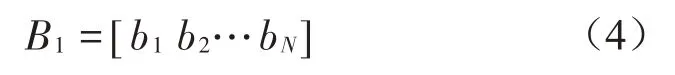
由于傾角儀和振動位移傳感器是由同1臺采集儀同步采集到的，因此，兩個數組里相同位置的數子是同一時刻采集儀到。則這時間段的塔筒頂部晃動位移數組為：

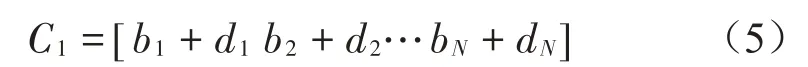
基于以上方法可求得塔筒頂部在主風向、垂直主風向兩個方向的晃動位移時程曲線。

2 基于模型實驗驗證

風力發電機塔筒為高聳結構建筑物，高度可達100 m，上部直徑為2 m～4 m左右，底端通過打樁或者澆筑混凝土固定，頂部可自由晃動，為典型的懸臂梁結構，所以本文使用懸臂梁結構對塔筒的晃動位移量進行模擬實驗，選取的梁結構尺寸接近于塔筒按比例縮小的模型。具體實驗過程如下。

把1 根長為5 m、寬0.2 m、高0.1 m 的工字梁的一端固定在一個水泥墩上，另外一頭懸空，在工字梁固定端和中間位置分別布置一個單向的QYG01-1傾角儀，在懸空端布置一個帶豎向位移和單向傾角輸出的QZDC-A 型多參量傳感器，及1 個拉線式位移計。實驗方法布置示意圖如圖1所示。工字梁的截面尺寸和使用的傾角傳感器如圖2所示。

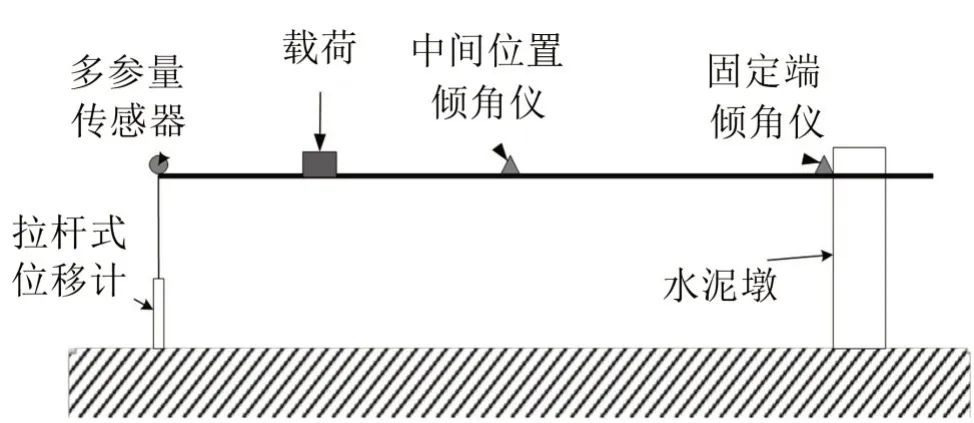
圖1 實驗方法示意圖

圖2 校準實驗照片

荷載加載情況和測量結果如表2所示。

由表2可見：傾角-振動位移計合成法相比純傾角儀法，得到的最大絕對位移值更準確。當荷載為靜態加載時，傾角儀法、拉桿式位移計法、傾角-振動位移計合成法測試結果都非常接近；當荷載為動態加載時，如以拉桿式位移計法為參考，則傾角-振動位移計合成法的測試結果誤差分別為-1.9 %、0.8%，而傾角儀法的測試結果誤差分別為-17.1%、-28.9%。實驗結果表明傾角儀-振動位移計合成法的測試結果精度較高，可達到至少毫米級的精度，改善了傾角儀法測量動態加載荷載的誤差較大的情況。因此，把振動位移計的測量時程波形同步合成到傾角儀法的時程波形，可明顯提高傾角儀法測量動態位移時的精度。

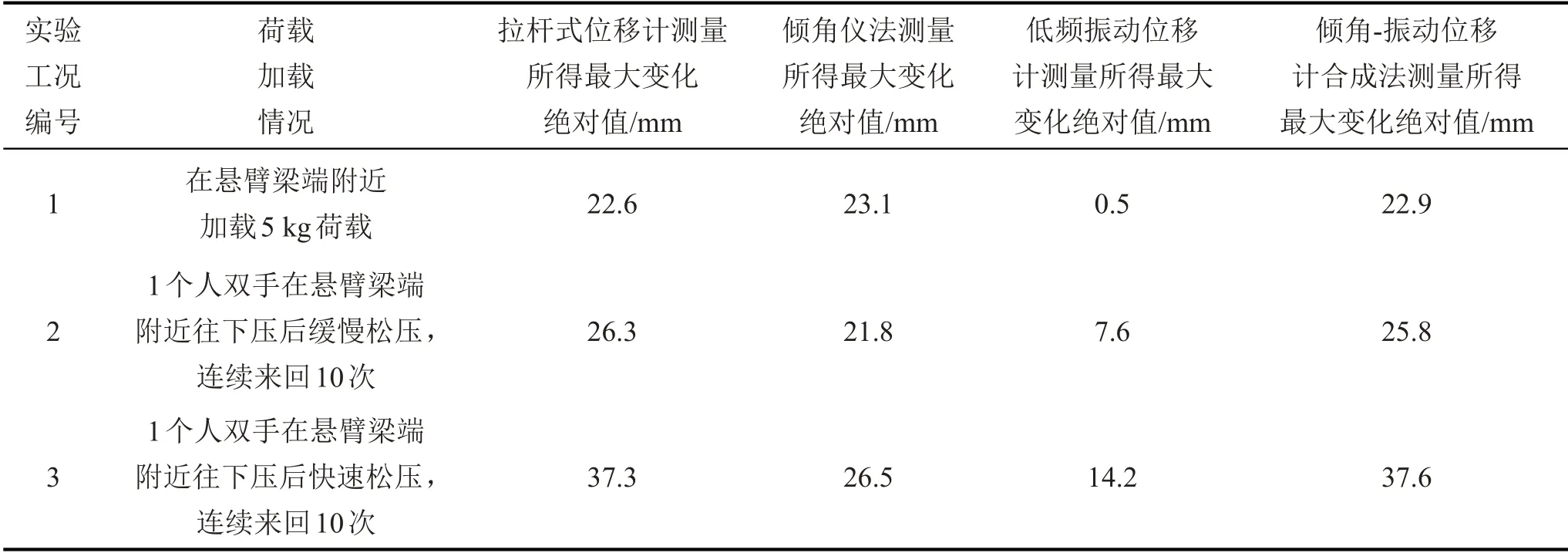
表2 實驗測量結果統計

本實驗模型測量原理簡單，計算過程干擾因素較少而且與被測量對象的結構無關，不會因為結構物不同而導致測量精度改變，可能會因為測量使用的儀器精度不同導致監測系統精度有所變化。

3 單樁基礎風機晃動位移實測數據分析

本文使用此方法對江蘇大豐縣的某個總裝機容量200 MW 海上風電場的2 座單樁基礎結構的風機塔開展了晃動位移的自動化監測。這兩座風機基礎為同類型的單樁基礎樁，打入淤泥35 m～50 m；基礎樁露出水面9 m～12 m；塔筒為3 節塔筒結構，基礎樁到塔頂高為97 m。機組為上海電氣的4 MW風機。機組圖片如圖3所示。

圖3 單樁基礎風機

典型的臺風風速曲線如圖4所示。繪制此時機組在臺風作用下的典型晃動位移時程圖如圖5所示。

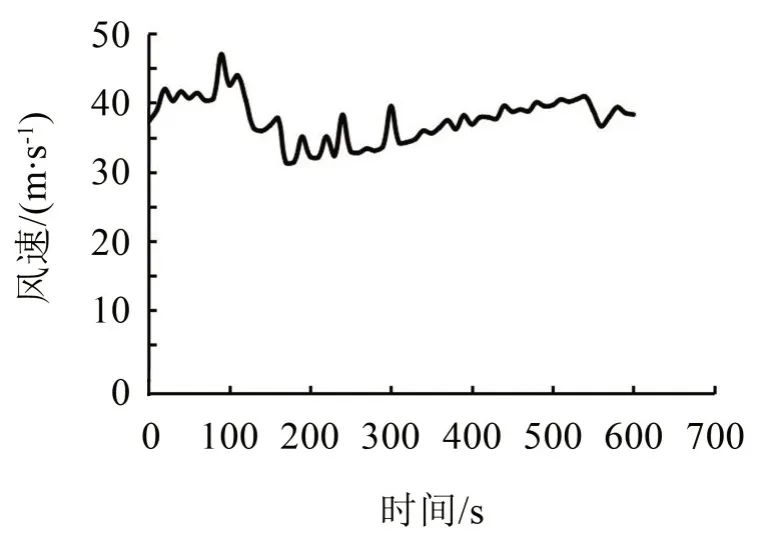
圖4 臺風期間的典型風速時程圖

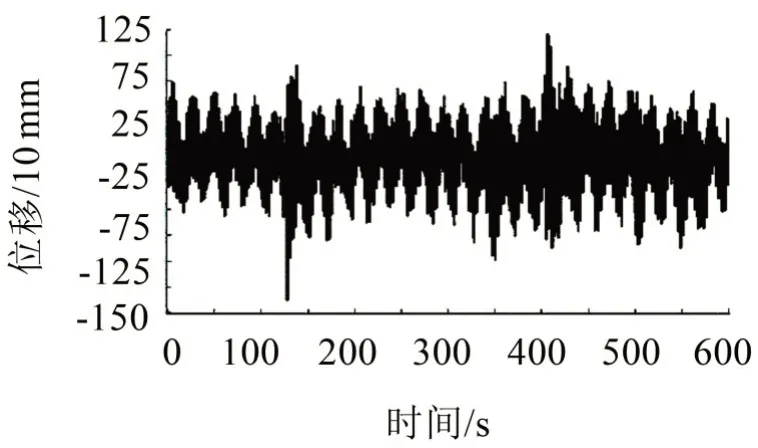
圖5 37#機組臺風作用下的典型晃動位移時程圖

為了更加全面地研究風力發電機的晃動位移情況，分偏航、臺風、工作狀態、和停機狀態4種工況進行晃動位移測試，偏航工況是指手動偏航360°的情況，臺風工況是指舜時風速介于30 m/s～45 m/s 的停機情況，工作狀態是指葉片轉動，瞬時風速介于10 m/s～15 m/s之間的情況，停機狀態是指瞬時風速介于5 m/s～8 m/s，發電機未發電的情況。統計風機塔在各種典型工況下的頂部晃動位移峰值如表3和表4所示。

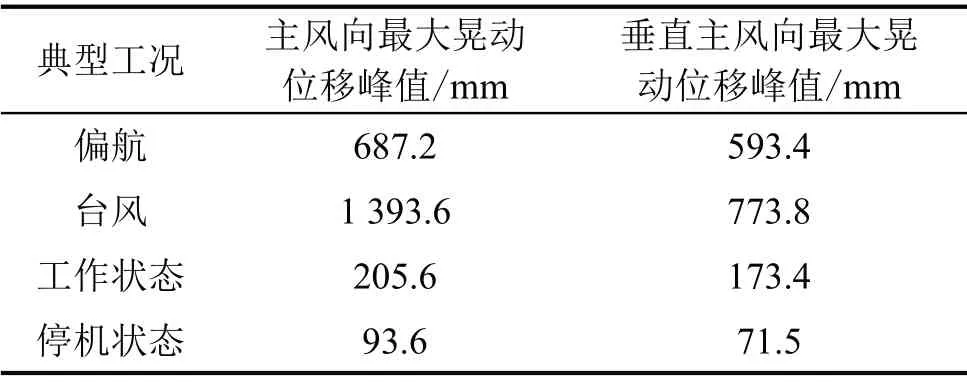
表3 47#風機各典型工況下的晃動位移最大峰值

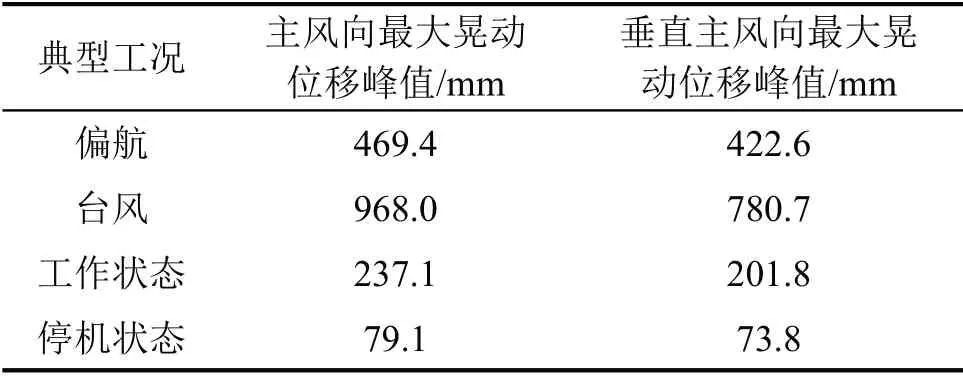
表4 58#風機各典型工況下的晃動位移最大峰值

由圖5和圖6可見：此類4 MW風力發電機塔筒頂部在臺風期間的晃動位移幅度較大，其頻譜在0.003 Hz、0.045 Hz、0.33 Hz 處比較突出。臺風發生時，風機一般做停機處理，0.33 Hz與塔筒1階固有頻率很接近，0.045 Hz 和0.003 Hz 可能與風速變化速率相關，所以臺風作用下風機塔筒主要振動為受迫振動和1階固有頻率的振動。

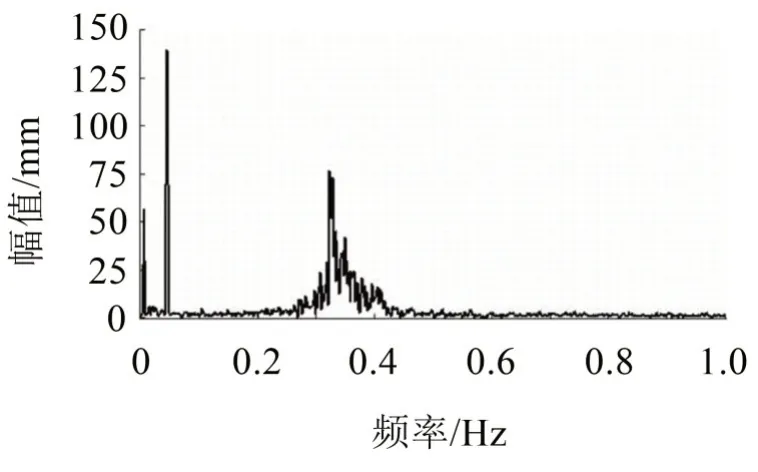
圖6 37#機組臺風作用下的典型晃動位移頻譜圖

由表3和表4可見：塔筒頂部在偏航狀態下的晃動位移最大峰值比正常運轉下的晃動位移最大峰值大2～3 倍，其中#47 號風機塔頂的位移值達到了687.2 mm。兩座風機塔在同樣的手工偏航360°的情況下，塔頂主峰向的最大晃動位移峰值分別為687.2 mm、469.4 mm差較大。這可能是#47號風機的偏航卡鉗老化較嚴重而導致其與齒輪的沖擊力較大，進而引起塔筒劇烈晃動。兩座風機在臺風作用下的最大晃動位移峰值分別為1 393.6 mm、968.0 mm，超過了其高程的1/100 的彎曲幅度。以上分析表明此類型風機塔在臺風期間、對風向偏航期間的晃動幅度都較大，應引起重視。

4 結語

本文分析了常見方法測量高聳建筑物晃動位移的不足之處，然后提出傾角儀法、低頻振動位移法同步采集和同步合成的新的測量方法。實驗結果表明傾角儀法-振動位移計法在動態荷載工況下的測量結果與拉桿式位移計測量結果比較，誤差小于2%，可達到至少毫米級的精度。

同時本文在兩臺4 MW風力發電機上進行了晃動位移實測，測試結果可以有效分析塔頂晃動的位移幅度和頻譜特性，發現臺風或偏航作用下塔筒頂部的晃動位移幅度較大，臺風作用下晃動位移超過了機組高程的1/100，偏航作用下風機的晃動位移接近正常運行時的兩倍，這兩種工況機組的安全狀況都值得進一步的研究；機組在臺風作用下振動除了集中在1 階固有頻率處外還集中在0.003 Hz 和0.045 Hz的頻率點，可能是因為風速、海浪等作用下導致的受迫振動頻率。

本文的研究提出了風力發電機晃動位移的測量的新方法，提高了晃動位移測量的精度，同時實測了兩臺風力發電機，豐富了海上風機塔筒晃動位移的研究資料。