基于參數激勵的兩自由度耦合MEMS諧振式陀螺

呂路婧，李 崇，綦聲波

（中國海洋大學 工程學院，山東 青島 266100）

MEMS諧振式陀螺是一種測量旋轉的慣性傳感器，與傳統陀螺儀相比，MEMS硅微陀螺儀具有體積小、重量輕、功耗低、可靠性高、成本低等眾多優點，可以更加廣泛地應用于消費電子、汽車電子以及國防科技等領域，因此在過去的幾十年中引起了業界的廣泛關注，但是也存在一些不容忽視的問題。

首先，振動陀螺儀利用諧振器的兩個正交模態之間的科里奧利力耦合，以達到檢測旋轉速率的目的。檢測模態要求最大限度地提高檢測電極的信噪比。通常，是在驅動模態上施加頻率與固有頻率相同的強迫信號來產生振動的。然而在低旋轉速率時，科里奧利力較小，檢測模態的振幅比驅動模態小1～2 個數量級。為了提高信噪比，需要提高強迫信號的振幅以使單位力的響應幅度最大化。其次，電容驅動及檢測方法被用于許多陀螺儀的設計，但由于寄生電容存在，驅動信號的電“饋通”到檢測電極，污染檢測信號，因此會限制陀螺儀的靈敏度。最后，過程和材料的變化不可避免地導致兩個正交模態之間的頻率失調，從而減少了能量的轉移。此外，在調諧陀螺儀設計中，因為驅動信號和檢測信號具有相同頻率，對任何被污染的信號進行電子濾波都是比較困難的。振動式MEMS 陀螺系統存在的這些不足促使著研究人員尋找一種更好的激勵方法。

自參數激勵法首次在1886 年被Rayleigh Baron、Hill 等[1]提出后，引起了學界廣泛的研究。直到最近十幾年，國內外的研究學者才將參數激勵應用于MEMS陀螺儀中。2005年至2010年，英國紐卡斯大學將參數激勵應用于MEMS諧振式陀螺儀，并發表多篇論文[2–6]分析參數激勵與外部強迫激勵組合共振對驅動響應的增益效果；2011年，不列顛哥倫比亞大學[7]報道了MEMS陀螺儀中使用參數激勵的放大和阻尼效應，驗證了通過調節驅動力和參數激勵之間的相位差，可以實現信號放大或不理想信號分量的衰減以及減少正交誤差；2013 年，伊朗Ali Pakniyat和Hassan Salarieh兩人研究了具有參數激勵的固有頻率匹配和失配的MEMS陀螺系統，數學模型為Duffing方程與Mathieu方程相結合的形式。結果表明，參數激勵能夠為頻率失配模式下的MEMS陀螺儀提供較高的精度和魯棒性[8]。2015 年，埃及梅努菲亞大學、沙特阿拉伯泰夫大學等[9]研究了具有線性和非線性參數激勵的兩自由度耦合的MEMS 陀螺儀振動的動力學、能量傳遞和控制。

根據以往的研究，對參數激勵的MEMS 陀螺系統的分析大多基于只有一個自由度的主模態（驅動模態）的數學模型，或者有兩個自由度但卻只有參數激勵而無外部強迫激勵的情況。而同時具有參數激勵與強迫激勵的兩自由度耦合的模型卻鮮有提出。在設計參數激勵方法時，應考慮模態耦合，因為有關的相互作用可能會大大改變機械器件的性能[10]。因此，本文研究在參數激勵和外部強迫激勵共同作用下兩模態耦合的諧振式MEMS陀螺系統，給出系統的動力學模型并采用多尺度法進行攝動分析，最后在龍格-庫塔法與牛頓迭代法進行數值求解的基礎上進行實驗仿真，分析耦合項對振動系統的影響，最后驗證參數激勵對振動響應的放大作用。

1 MEMS陀螺系統工作原理及模型

1.1 工作原理與理想情況模型

振動陀螺儀是基于圖1所示的科里奧利力來工作的。進行直線運動的質點在旋轉體中會因慣性而產生偏轉，相對于旋轉體，運動軌跡為曲線。可以認為有一個力存在，正是這個力使質點的運動軌跡發生了改變，這個假想力即為科里奧利力。

圖1 科里奧利效應

諧振式MEMS 陀螺儀的理想模型如圖2所示，其力學模型可以看作一個兩自由度的彈簧-質量-阻尼系統。在此系統中，傳感器的一個模態表現為受外部強迫激勵（一般為正弦信號，如圖2中的Fx）總是沿一個方向振動，稱為驅動模態，如圖2中的x軸；當傳感器外部存在繞z軸旋轉的角速率ΩZ時，另一個模態表現為產生的科里奧利力Fcy會在一個或多個方向上引起振動，稱為檢測模態，如圖2中的y軸。通過檢測振動的大小即可求出旋轉角速率。

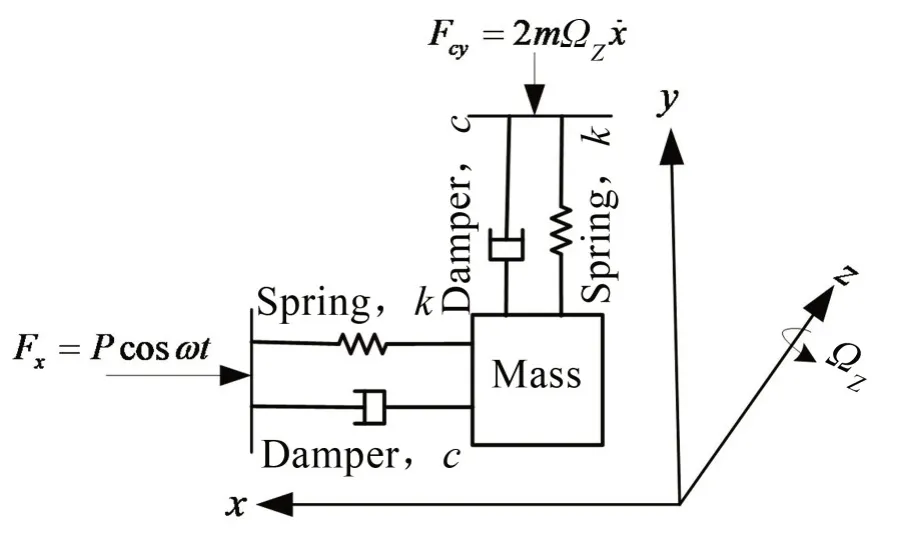
圖2 振動式微陀螺理想模型

假設沿x軸方向為驅動模態，沿y軸方向為檢測模態。理想情況下，由于內部結構的高度對稱性，可認為兩模態的質量m、阻尼系數c以及彈簧系數k均相同。此時系統的運動方程如下：

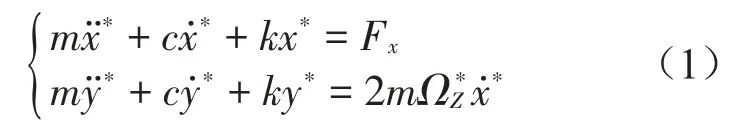
其中：‘*’表示無量綱前的實際值；m，k，c分別表示質量、剛度、阻尼系數；x*，y*為兩個方向的位移；Fx為外部強迫力；Ω*Z為外部旋轉角速率；2mΩ*Z為科里奧利力。

x軸的振蕩主要由該方向上的靜電力Fx提供。y軸方向的振動則主要由系統繞z軸的轉動產生的科里奧利力2mΩ*Z引起。

1.2 含有參數激勵的非理想情況模型

在實際情況中，由于材料和工藝等都是在微尺度上加工制造，所以旋轉部件在運動過程中面臨著許多問題。例如，由于設備中缺乏完美的對稱性，可能產生非理想彈簧力；或者由于系統中結構阻尼等各種物理原因導致能量在懸梁之間傳輸而造成損失。所以陀螺系統的實際模型如圖3所示，系統中兩個模態的剛度和阻尼均不相同且存在交叉耦合。

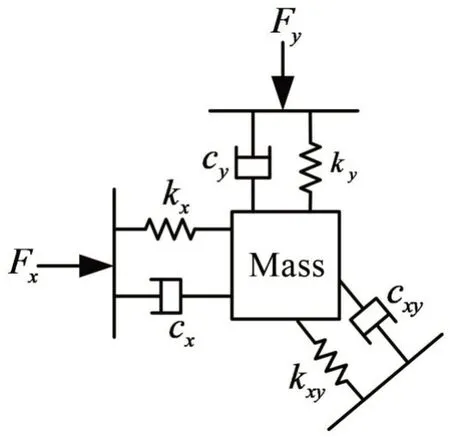
圖3 振動式微陀螺非理想模型

參數激勵諧振器是指至少有一個物理參數(即質量、阻尼或剛度)在時間上周期性變化，導致振動系統達到諧振狀態并且動態響應具有特殊的性質[11]。當參數輸入是周期性變化的彈簧剛度時，運動可以由方程（2）描述：

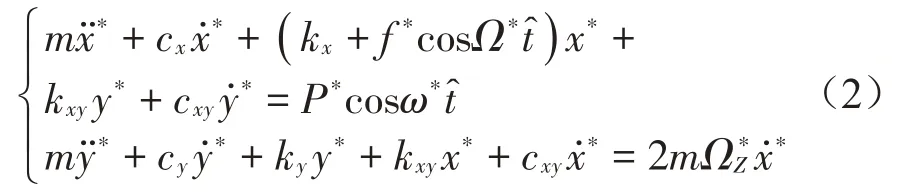
其中：m，kx、ky，cx、cy分別為質量、剛度、阻尼系數；cxy、kxy分別為耦合阻尼系數與耦合剛度系數；x*·f*cosΩ*代表參數激勵項；P*cosω*為外部強迫力；2mΩZ*為科里奧利力。

2 陀螺兩自由度方程攝動法分析

2.1 方程無量綱化

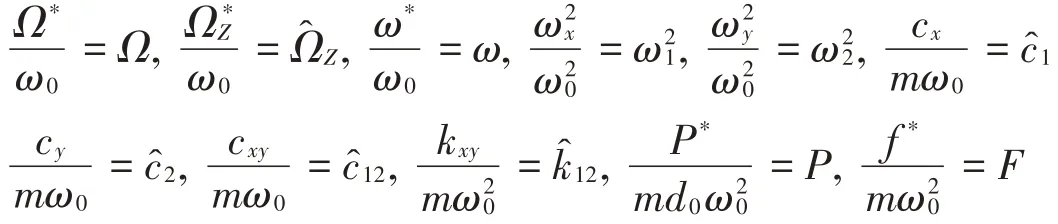
經整理后得到陀螺系統無量綱方程式如下：

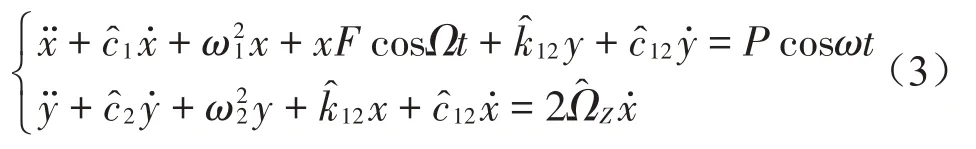
2.2 多尺度攝動法分析

由于多尺度攝動法對線性或非線性系統均適用，求解結果更為精確，尤其對阻尼系統的處理也更為方便，因此采用多尺度法對方程式（3）進行求解。引入小參數ε，設方程式（3）解的形式為：

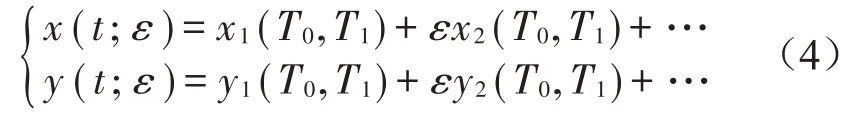
其中：T0=t,T1=εt…，并且定義微分因子：

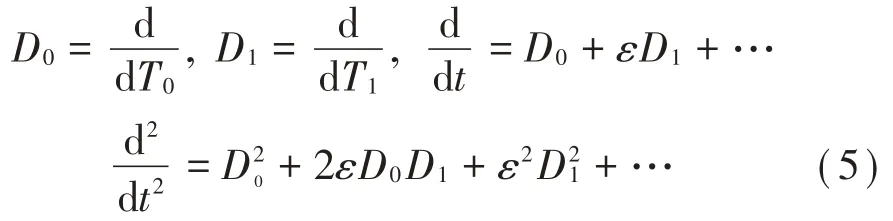
及參數尺度：

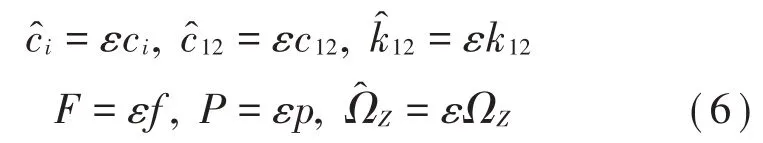
將式（4）、式（5）、式（6）代入方程式（3）并且使ε的同冪系數為零可得：

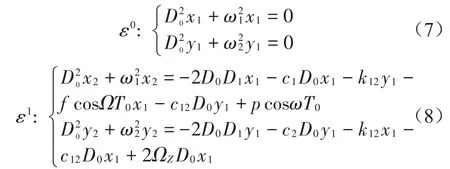
設方程（7）的解形式為：

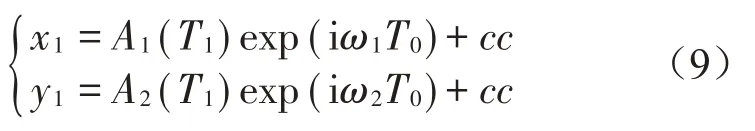
其中：cc代表前一項的復數共軛，將式（9）代入式（8）中得：

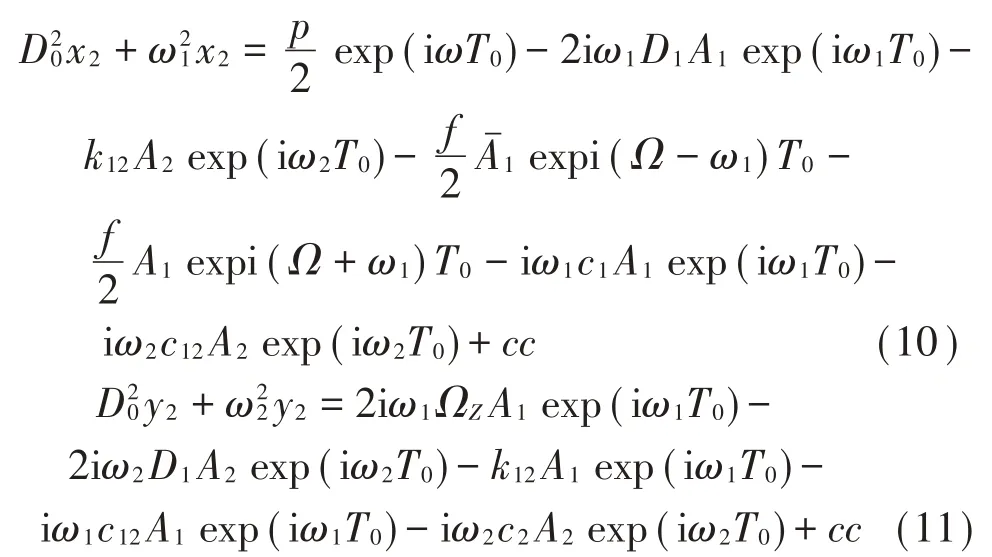
將兩個模態的振幅分別寫為極坐標形式：A1 =，a、b、β均是關于尺度時間T1的函數。

根據共振的概念[12]，我們主要關注的是外部共振中的主共振和主參數共振以及1:1內部共振，因此可以將系統中各頻率的關系用以下方式表達：（1）對于內部共振，應滿足ω1≈ω2，引入失調參數σ后寫成ω2=ω1+εσ；（2）對于主共振，發生在ω≈ω1，引入失調參數σ1后寫成ω=ω1+εσ1；（3）對于主參數共振，令Ω=2ω，則參數激勵頻率可以寫成Ω=2ω1+2εσ1。將以上頻率代入方程式（10）、式（11），消除長期周期項，得到可解條件為：

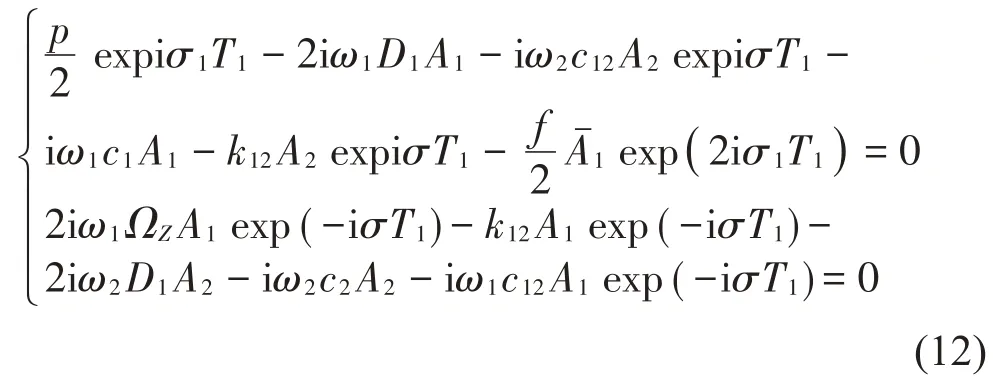
σ1T1-β1=γ1,(σ1-σ)T1-β2=γ2

2σ1T1-2β1=2γ1,β1-β2-σT1=γ2-γ1

化簡并分離實部虛部得：

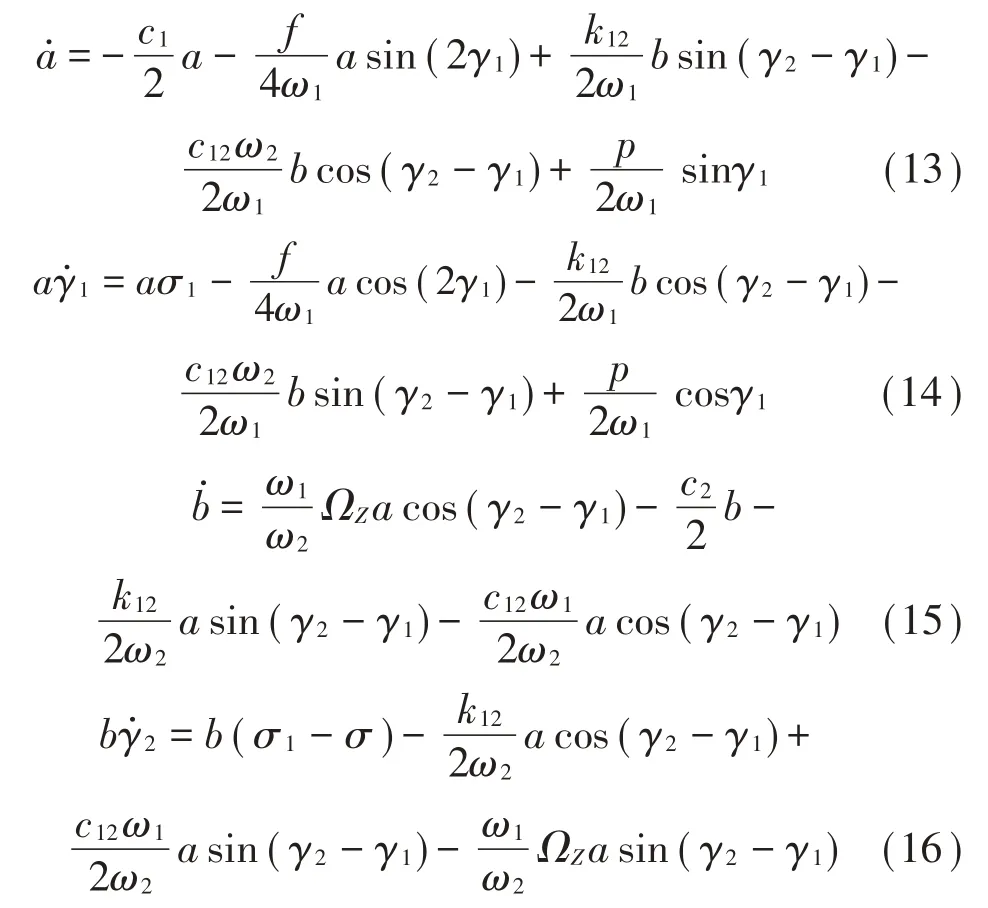
由參數激勵產生的能量輸入系統中會引起響應振幅的增加，理論上是無限大的，但是系統中的阻尼會限制振幅的繼續增加，穩態運動發生在能量輸入的速率恰好等于耗散的速率。在這種情況下滿足，此時得到方程式（17）至式（20）：

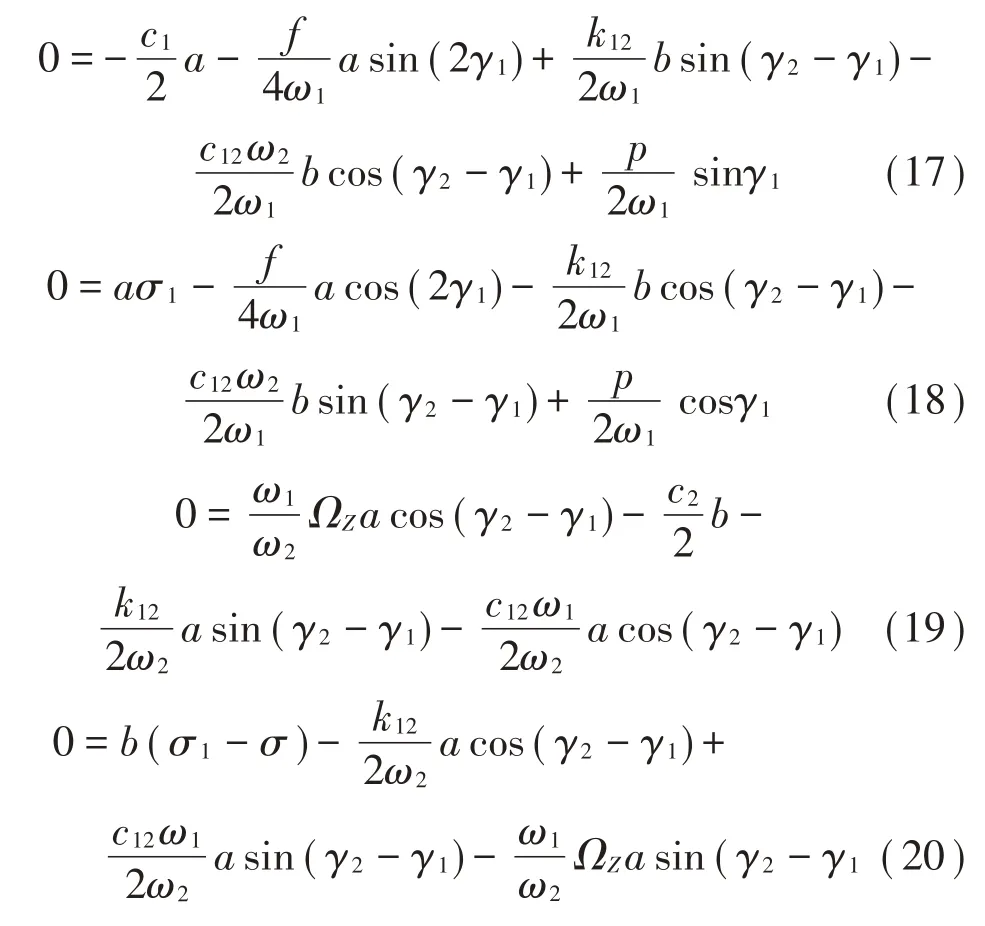
因此可以通過數值求解方程式（17）至式（20）得到參數激勵和強迫振動共同作用下的頻率響應曲線。

2.3 參數激勵閾值

在實際情況下，參數激勵振幅f的取值并不是無限增大的。f在某一范圍，響應振幅是穩定震蕩的，但若超出穩定的閾值則會使響應發散，從而進入不穩定區。因此需要對參數激勵振幅的閾值進行分析。由方程式（17）至式（20）整理可得：

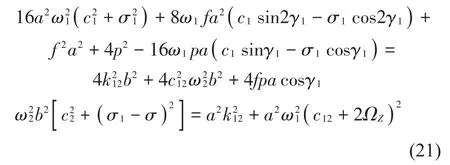
當外部旋轉ΩZ=0 時，可以得到參數激勵振幅的閾值為：

從式（22）可以看出，參數激勵的閾值不僅與系統模態本身的阻尼c1、c2有關，而且與耦合阻尼c12及耦合剛度k12也有關。

3 數值仿真及結果分析

3.1 數值求解

參考典型的陀螺設計，本文進行驗證所采用的陀螺參數如表1所示。仿真環境為Mathworks MATLAB R2017b。

表1 MEMS陀螺系統物理參數

采用四階龍格-庫塔法和牛頓迭代法分別對方程組（13）至式（16）、式（17）至式（20）進行數值求解，以研究各參數對驅動模態和檢測模態的時域響應及頻域響應的影響。

3.2 頻率響應結果分析

通過牛頓迭代法求解方程式（17）至式（20）可以得到幅頻響應曲線。方程中小參數選擇為ε=0.01，初始無量綱耦合系數k12和c12分別取驅動模態本身的10%，即c12=0.1c1，k12=0.1k1。其他無量綱參數選擇如下：外部強迫力振幅為p=0.015，令外部角速度輸入ΩZ=0,模態間頻率失諧參數為σ=0.5（由ω1=1，ω2=ω1+εσ，此時ω2=1.005）。

首先研究參數激勵作用的影響，頻率響應曲線如圖4所示。

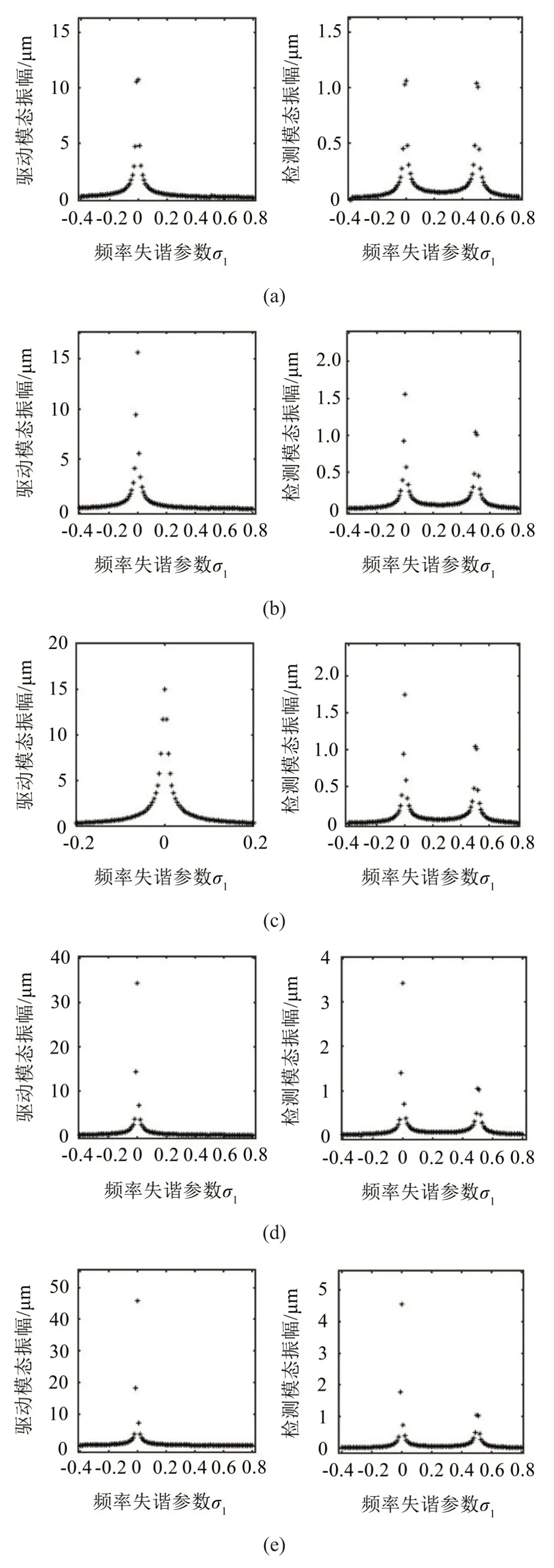
圖4 參數激勵影響下的幅頻響應曲線

為了說明有參數激勵與沒有參數激勵兩種情況下的結果，設置了圖4（a）與圖4（b）兩組數據。其中圖4（a）是沒有參數激勵只有外部強迫力的情況，即無量綱振幅f=0，p=0.015，圖4（b）為其他參數不變，加入參數激勵力，使其振幅為f=0.01。從兩幅圖的對比可以看出，在模態間頻率失匹配情況下，加入參數激勵后會導致驅動模態與檢測模態響應振幅的增大，并且在σ1=0 處（根據ω=ω1+εσ1，外部強迫力頻率與驅動模態頻率相同，即ω=ω1）產生主共振，響應最大；當σ1=0.5時，外部強迫力頻率等于檢測模態的頻率，即ω=ω2，也會使檢測模態在此處產生共振。

圖4（c）考慮參數激勵作用處于穩定區的情況，在圖4（b）的基礎上稍微將參數激勵振幅增大至f=0.012。圖4（b）與圖4（c）對比說明，在參數激勵振幅較小，處于穩定區時，激勵的效果并不明顯，響應振幅變化很小。

圖4（d）和圖4（e）則考慮逼近非穩定區的情況，仍然保持強迫振幅不變而將參激振幅分別取為f=0.02 和f=0.022。和處于穩定區的變化相對而言，圖4（d）與圖4（e）雖然激勵振幅也變化了0.002，但隨著參數激勵振幅增大將要接近不穩定的閾值時，激勵作用增強，響應振幅變化明顯。

圖5主要探究了低轉速下兩個正交模態之間的相互耦合作用對頻率響應的影響，令外部旋轉角速度為ΩZ=0.001。

圖5（a）為既沒有耦合項也沒有參數激勵項的情況，即f=0，c12=k12=0。由于此時接近理想情況，兩個模態諧振頻率幾乎相等，所以模態頻率失調參數設置為σ=0.1（即ω2=1.000 1），此外令強迫振幅p=0.015。從圖中可以看出：在沒有耦合項的情況下，共振產生的位置也與圖4相同，即系統會在強迫頻率等于驅動模態固有頻率（即ω=ω1）處產生主共振，并且當強迫頻率失調至等于檢測模態頻率時，也會使檢測模態產生共振。但相比圖4（a）可以發現，在沒有耦合項時，驅動模態振幅增大，檢測模態振幅減小。

為了說明耦合剛度產生的影響，在圖5（b）中將耦合項系數設置為c12=0.1c1，k12=0.1k1，其他與圖5（a）相同，而圖5（c）則保持其他參數不變，只將耦合剛度增大至k12=0.2k1。可以發現，隨著耦合剛度的增大會使強迫頻率在驅動模態固有頻率附近向左偏移時（圖（b）在σ1=-0.02 處，圖（c）在σ1=-0.06 處）產生共振，并且會在此時使驅動模態振幅不斷減小，檢測模態振幅不斷增大；而其在檢測模態固有頻率

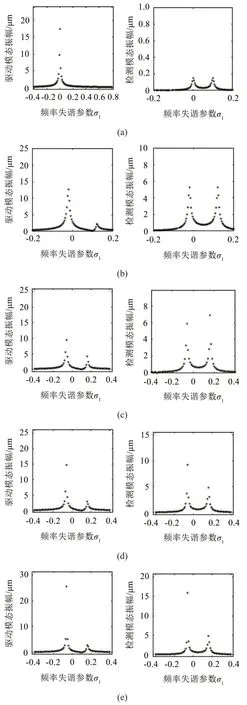
圖5 耦合項影響下的幅頻響應曲線

附近向右偏移同樣的量時（圖（b）在σ1=0.12處，圖（c）在σ1=0.16 處）也產生共振，而且會使驅動模態和檢測模態的振幅均增大。

為了探究耦合阻尼的影響，在圖5（c）的基礎上將耦合阻尼增大至c12=0.5c1，其他參數不變，如圖5（d）所示。可以看出，耦合阻尼的增大，會使強迫頻率在驅動模態固有頻率附近時，兩個模態的振幅均增強，而在檢測模態固有頻率附近時兩個模態的振幅均減弱。

為了說明在耦合阻尼與耦合剛度同時存在的不理想情況下，加入參數激勵后的作用，因此在圖5（d）的基礎上加入了參數激勵項，見圖5（e），振幅取值為f=0.01。圖5（e）說明，參數激勵會同時放大兩個模態的響應振幅，但參數激勵振幅的加入卻不能調整由耦合剛度引起的共振頻率偏移。

3.3 時域響應結果分析

通過數值求解方程式（13）至式（16），可以得到如圖6所示的時域響應曲線，其結果與圖4、圖5的頻率響應曲線吻合。

圖6（a）為無耦合項的情況，且也沒有參數激勵，只有諧波強迫單獨作用于陀螺驅動模態。此時，取σ=0.1，σ1=0，ΩZ=0.001，c12=k12=0，f=0，p=0.015。從圖中可以看出，在模態間無耦合作用并且兩個模態固有頻率幾乎完全相同（σ=0.1 時，ω2=1.000 1≈ω1=1）的理想情況下，陀螺系統在σ1=0處產生了主共振，并且兩個模態的響應振幅相差兩個數量級。

圖6（b）保持其他參數不變只加入耦合項，其中耦合阻尼c12=0.1c1，耦合剛度k12=0.1k1。圖6（c）在圖6（b）的基礎上，只改變了強迫頻率失調參數，使其為σ1=-0.02。從圖7（b）和圖7（c）中可以看到，當兩個模態間存在阻尼耦合與剛度耦合時，在σ1=0處只存在較小的振動，并沒有產生共振，而在σ1=-0.02時產生了共振，并且由于耦合作用，造成驅動模態共振時振幅減小，檢測模態振幅增大，導致兩個模態數量級拉近。說明耦合項的加入會使主共振頻率發生偏移以及會對響應振幅產生影響。

圖6（d）補充說明了共振頻率偏移與響應振幅變化到底是由何種耦合引起的。在圖6（d）中單獨增大耦合阻尼至c12=0.5c1，其他參數同圖6（c）。圖6（d）與圖6（c）對比說明，共振頻率的偏移是由耦合剛度引起，耦合阻尼的增大并沒有引起共振頻率偏移，只是會使共振振幅稍微增大，而耦合剛度是引起兩個模態共振幅值差距縮小的主要原因。

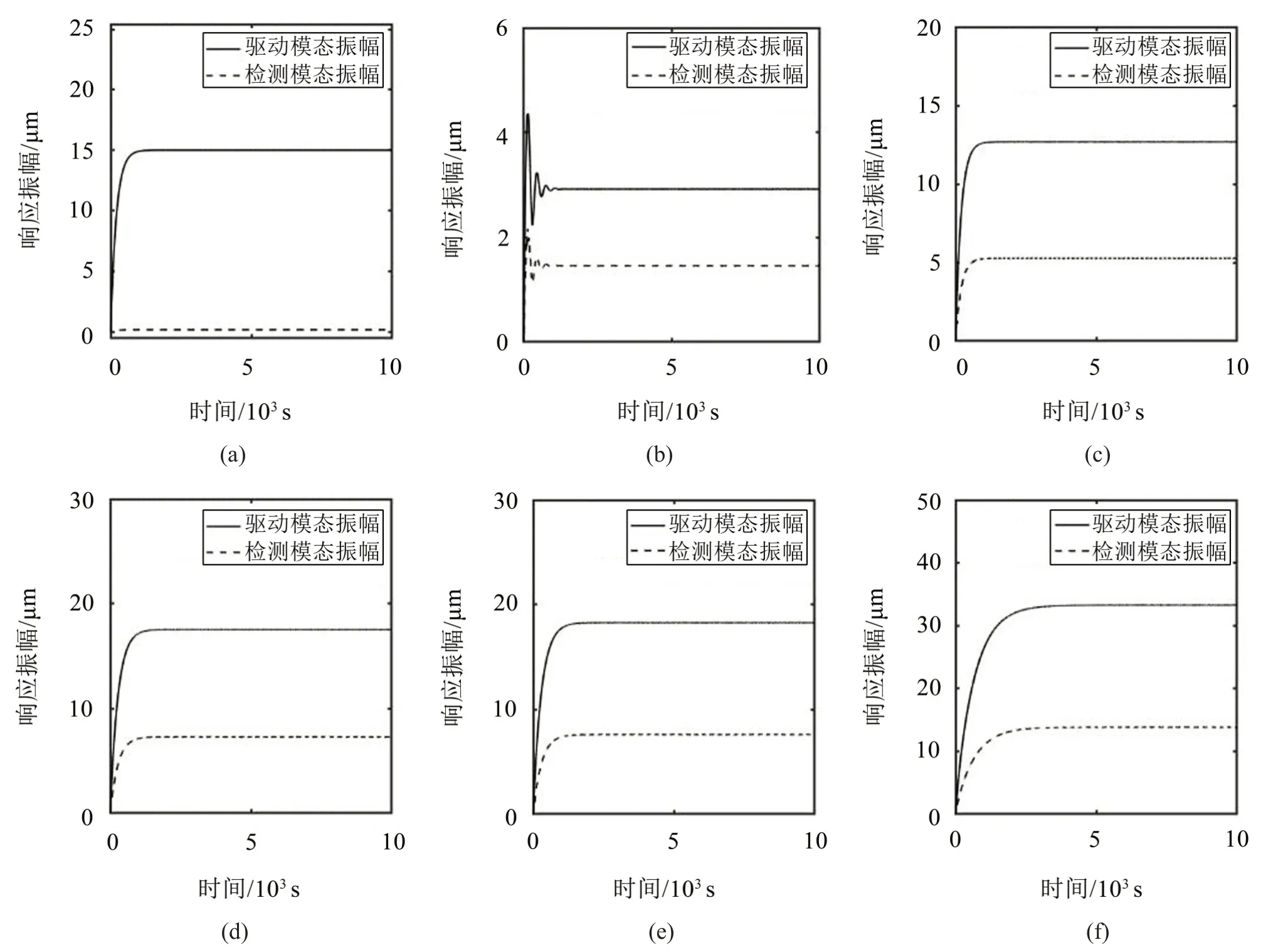
圖6 不同參數下的時域響應曲線

圖6（e）與圖6（f）則是考慮存在耦合因素的非理想情況下，在系統中加入參數激勵作用后的效果，只是激勵強度不同。圖6（e）中f=0.002，圖6（f）中f=0.01，其他參數同圖6（d）。圖6（d）、圖6（e）、圖6（f）對比可以看出，參數激勵確實會放大響應振幅，并且在一定范圍內呈非線性作用且效果明顯。但只調節參激振幅并不能改變由耦合剛度引起的共振頻率偏移。

圖7是將圖6中的穩態部分放大后看到的曲線，說明系統的穩態解是周期函數，MEMS 諧振器產生周期振動。

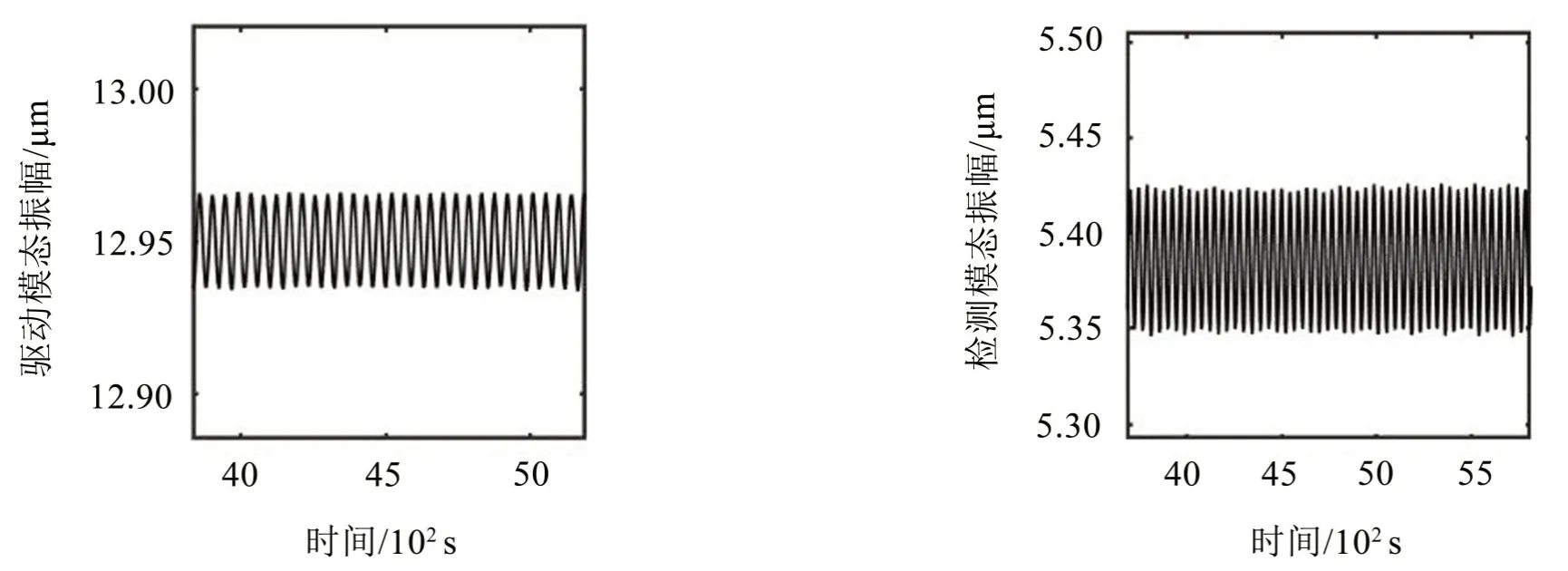
圖7 穩態響應曲線

3.4 耦合項對參數激勵振幅閾值的影響

給定參數ΩZ=0，σ=0.5，p=0.015，進行數值計算，找出使兩個模態振幅開始趨于非線性放大時的參激振幅，研究耦合系數對參數激勵振幅閾值的影響，結果如表2所示。

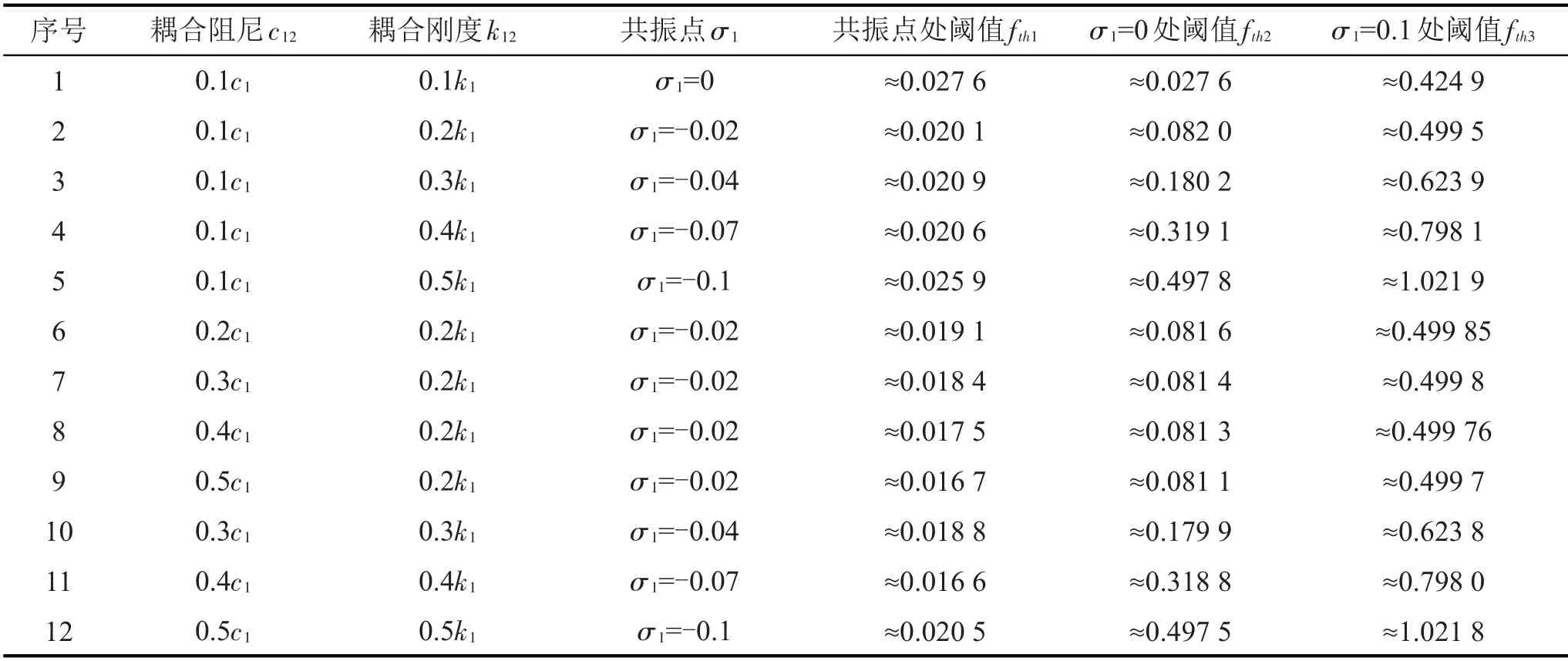
表2 耦合項系數變化對參數激勵振幅閾值的影響

在表2中，1～5組數據為保持耦合阻尼不變，單獨增大耦合剛度，此時會造成共振頻率偏移，從而導致在不同的耦合剛度下共振頻率各不相同，且耦合剛度對參激振幅閾值影響無規律可言，有時使其增大，有時使其減小，但總體來說對閾值的影響較小；而對于非共振點處（如σ1=0或σ1=0.1），耦合剛度增加會大幅提升參激振幅閾值。6～9組數據為保持耦合剛度不變，單獨增大耦合阻尼，此時共振頻率不會發生偏移，而且對于共振點和非共振點來說，耦合阻尼的增大對參激振幅的閾值影響均很小。10～12組數據為耦合剛度與耦合阻尼同時增大的情況，產生的作用依然會導致共振頻率改變且會使非共振點處的參激振幅閾值大幅提升。

4 結語

本文主要研究了諧振式MEMS 陀螺系統，建立了參數激勵與強迫力共同作用下的兩自由度振動系統數學模型，并在模型中考慮了由于各種不利因素產生的耦合作用項。通過多尺度攝動法對系統進行分析推導，并采用牛頓迭代法與四階龍格庫塔法進行數值求解和仿真試驗，驗證了參數激勵的放大作用，此外針對耦合項得出以下結論：

（1）耦合剛度的增大能夠造成主共振頻率向左偏移，即在強迫頻率小于驅動模態固有頻率的情況下產生共振，并且會使共振時驅動模態振幅減小，檢測模態振幅增大。此時若忽視了耦合剛度的存在，仍以驅動模態固有頻率強迫共振的話，檢測到的振幅并不是共振下的情況，而且信號也會很弱和不準確；但如果采取優化控制器、反饋調頻等措施，善加利用這種現象則會有利于提高信噪比和降低系統功耗。

（2）耦合阻尼的增大，會使強迫頻率在驅動模態固有頻率附近時，兩個模態的振幅均增強，而在檢測模態固有頻率附近時兩個模態的振幅均減弱。

（3）參數激勵的閾值決定著穩態解的穩定性，而耦合剛度和耦合阻尼對參數激勵的閾值均有影響，但耦合剛度的影響更明顯一些。

綜上所述，耦合剛度與耦合阻尼存在于系統中，會導致模態間能量的傳遞。對于含有耦合項的參數激勵與強迫激勵共同作用下的兩自由度陀螺系統，其動力學特性是比較復雜的。為了更全面地進行分析，建議下一步首先建立更加完善的數學模型，如在現有模型的基礎上發展非線性耦合或者檢測模態的參數激勵，并且采用除了多尺度分析法、數值求解法之外的新方法分析系統，從而更好地分析系統的動力學特性；其次，在MEMS陀螺的設計過程中，除了在工藝上考慮材料選擇、機械加工、電路設計等因素外，由于溫度和壓力會改變穩定-不穩定邊界的位置，導致放大效果顯著降低，因此還應該采取措施消除環境擾動，如優化閉環控制回路，以提高參數放大的穩定性和放大效果。