數學黑洞495的Python求解和驗證

丁大為 王德貴

通過前期的文章，我們了解了“數學黑洞6174”，也確實感到了數學中的玄妙。卡普雷卡爾（Kaprekar）黑洞，又稱重排求差黑洞，其計算過程稱為卡普雷卡爾運算，這個現象稱歸斂，“6174”稱歸斂結果。四位數的黑洞是“6174”，那三位數有同樣的黑洞嗎？

今天我們用Python來求解和驗證。

數學黑洞問題，經過幾天的研究，真的感覺很有意思，那么除了四位數的6174，三位數、五位數是不是也有類似的規律呢，這期分享三位數的黑洞。

找到三位數的數學黑洞是一個求解和驗證的問題，也要解決以下三個問題。

一是輸入任意一個三位數（不包含全部相同的數字），驗證最后經過運算是不是得到一個固定的值;二是在一定范圍內，是不是所有數都能得到這個固定值;三是要得到這個值最多需要多少步驟。

思路與四位數驗證一樣，首先要將三位數分解開單個數字，存儲在新列表中，然后排序列表，輸出最大和最小數，做差，然后再存儲在新列表中，循環操作，看看最后是不是得到一個固定的值。

程序涉及的是中國電子學會編程等級考試四級知識點。

1.求解

即求解三位數的歸斂結果，是什么樣的數據。

參照四位數驗證方法，程序設計（如圖1）。

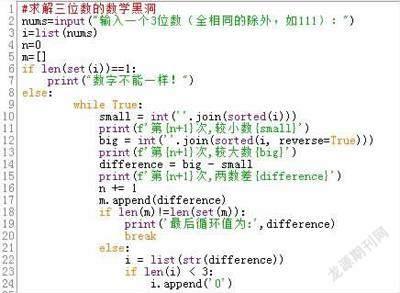
將輸入的三位數轉化為列表，然后判斷數字是否完全相同，如果不完全相同，則循環執行將列表中的三個數字排序，取出最大和最小的數，做差，在屏幕上顯示出來，同時添加到列表m中，如果有歸斂結果，則會有重復數據，于是判斷列表的長度和轉換為集合后的長度比較，如果不相等，則輸出最后一個數據，即為歸斂結果。

比如輸入：123，運行結果（如圖2）。

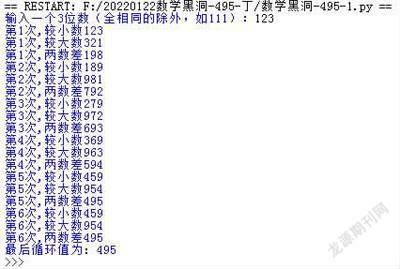
大家可以看到，歸斂結果為495！那其他三位數也是歸斂結果嗎？下面我們來驗證一下。

2.驗證

即是輸入任意一個數字不完全相同的三位數，進行驗證，看看能不能得到495，需要幾步。這里利用了自定義函數。

（1）遞推法

輸入一個三位數，但三個數字不能完全相同，將其轉換為列表，排序、連接、轉換出最大值和最小值，做差，再轉換為列表，如果不夠3位，則添加“0”，進行下一輪循環，直到得到“495”，然后輸出轉換用了多少次（如圖3）。比如驗證輸入123，5次后獲得結果495。

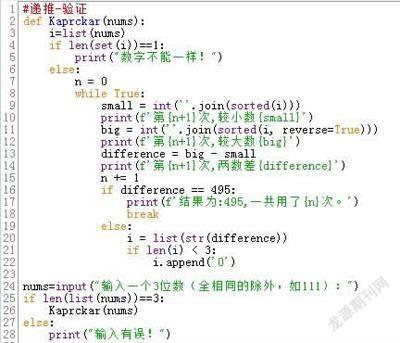
（2）遞歸法

遞歸與遞推的不同之處，是調用了自身，達到循環的目的。過程和方法與遞推類似。不同的是，遞推算法中第7行的n=0去掉了，這是因為如果加上這行，每次調用自身的時候，n都會歸0，不能計數，因而必須先設置n=0，然后在自定義函數中用“global n”。兩種方法驗證的結果是完全一樣的（如圖4）。

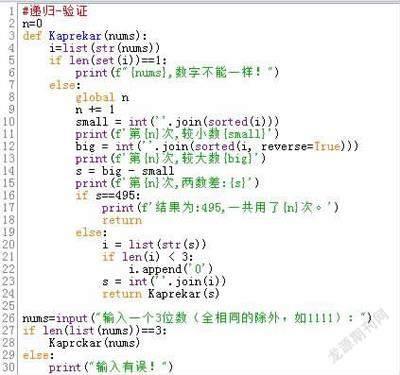
3.范圍

即是驗證一定范圍內所有數字不完全相同的三位數，看看能不能得到495，在這個范圍內需要最多的步數是多少。

（1）遞推法

通過遞推法驗證（如圖5）。

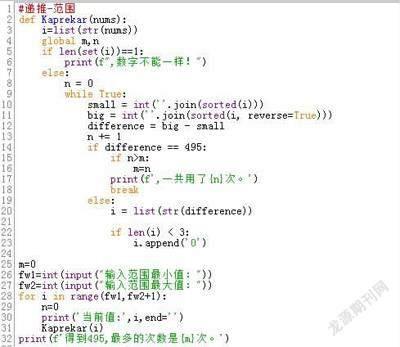
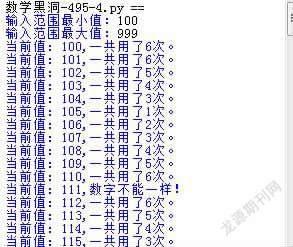
下面是在100-999范圍內的遞推法驗證，即所有三位數的驗證結果。在數字完全一樣時，給出提示，從驗證結果看，所有不完全相同的三位數，經過運算均可以得到“495”，并運算的最多次數是“6”（如圖6）。

（2）遞歸法

遞歸法和遞推法一樣，也是在驗證的基礎上，驗證一定范圍內的所有整數，經過運算是不是都能得到“495”，并輸出最多的運算次數。不同的是遞歸是通過調用自身，達到循環的目的。

同樣，遞歸法需要將遞推算法中的n=0去掉，而在遍歷前設置n=0，然后在自定義函數中設置為“global n”。m為最大次數變量（如圖7）。

下面是在100-999范圍內的遞歸法驗證，即所有三位數的驗證結果。在數字完全一樣時，給出提示，從驗證結果看，所有不完全相同的三位數，經過運算均可以得到“495”，并運算的最多次數是“6”（如圖8）。

我們看到，兩種方法的驗證結果是完全一樣的。

通過驗證，遞推和遞歸方法得出的結果完全相同。這是在“6174”驗證的基礎上，修改程序后，比較容易得到的。那你注意到三位數和四位數在驗證的時候，有什么相同點和不同點嗎？

我們只用Python做了驗證，有興趣的老師和同學可以參考“6174”的方法用Scratch和APPInventor去驗證。

本文是我自己的研究過程和心得，有不妥之處，請各位老師和同學斧正！