基于數學建模思想和數學文化的高數教學設計
——以導數概念為例

陳金雄，張 敏

武夷學院，福建 武夷山 354300

隨著中國經濟社會的高速發展，作為基礎學科的數學也越來越重要。大學生應用數學能力的培養載體之一是數學建模，數學建模是針對某個實際問題，或出于某個特殊的目的，按照其內在規律性，通過適當的假設，并使用相應的數理工具，從而得出一些數學模型，經過求解模型問題并得出結果以及檢驗結論是不是真實、合理的全過程[1]。高等數學是我國理工科、經管等各類專業的最主要的學科基礎課之一。如果能把數學建模融入高數的教學中，不僅有利于讓學生了解數學模型和數學建模的過程，而且能讓學生應用數學解決生活實際問題和提高學生學習高數的興趣，進而促進專業課的學習。同時，在高數課堂中，合理的穿插高等數學的歷史文化，既便于學生受到高等數學的歷史文化的陶冶，也培養了學生對學習高數的興趣，有利于發揮課程思政的育人功能。因此，在日常高等數學的教學設計中，融入建模思想和數學文化是非常有必要。

1 教學目標分析

利用實際案例，讓學生再復習高中學過的平均變化率、瞬時變化率，從而深入學習平均變化率如何求解瞬時變化率的過程，進而掌握對于瞬時變化率的表達式，也就是導數，體會無窮小思想，掌握數學建模、數學抽象的能力。教學重點主要是導數定義和利用定義求解簡單函數的導數的方法；教學難點是理解導數定義。然后，結合生活實例、數學建模和高等數學歷史文化，選擇了導致微積分誕生的變速直線運動和曲線過定點切線的兩個實際問題，讓學生充分體會利用無窮小的思想，進而更好地理解了由平均變化率求得到瞬時變化率，最后概括總結出導數的概念。

2 學情分析

學生在高中時代就已掌握了平均變動率、瞬時變化率、曲線切線等知識，并且已經初步學習了導數概念、實際意義和簡單導數的公式。但由于導數定義本身的高度概括，教師要適當地引導。先介紹學生比較熟悉的奧運英雄蘇炳添和全紅嬋，并將兩人在比賽中所做的變速直線運動和曲線的切線問題作為背景引入，發揮課程思政的作用，學習奧運英雄堅持不懈、永不言棄的良好品質，進而調動學生學習的興趣。引導學生對瞬時速度和曲線的切線斜率進行建模，并通過實例檢驗模型的準確性和有效性，然后抽象概括得到導數的定義，讓學生體會數學建模解決實際問題的過程。

3 教學過程

教學的主要過程設計如下：（1）提出問題：求解變速直線運動的瞬時速度、過曲線定點的切線斜率。（2）分析問題：利用無窮小思想，平均速度趨于瞬時速度或割線的斜率逼近切線斜率。（3）建立模型：瞬時速度等于平均速度的極限值、切線斜率等于割線斜率的極限。（4）求解模型、檢驗模型：采用特殊例子求解模型，依據高中的導數公式驗證模型的正確、合理性。（5）推廣模型：由以上兩個模型推廣到函數瞬時變化率，并由此得出導數的定義。（6）運用模型：理解導數概念，掌握求導步驟，應用計算結果解釋瞬時變化率的意義。

3.1 引例

3.1.1 變速直線運動的瞬時速度的求解

（1）提出問題

從“東京奧運英雄”的事跡導入:據報道，在日本東京奧運會百米半決賽賽中，蘇炳添跑出了9秒83的驚天成就并突破了亞洲記錄，同時他也作為中國國內第一個進入奧運會男子一百米淘汰賽的選手，也是時隔89年后亞洲人又一次進入奧運會百米飛人的半決賽;東京奧運會之后，他參加了他的第四屆全運會并首次奪得全運會的男子百米冠軍。東京奧運會中國奧運代表團最年輕的14歲小將全紅嬋，在東京奧運會跳水女子10m臺中，以三跳滿分的超大優勢拿到金牌，并打破陳若琳保持的決賽總分紀錄。他們的成功都是通過日積月累的努力拼搏，憑著永不言敗的堅韌品質獲得的，是通過每天進步一點點的量變變為取得歷史性突破的質變的必然結果，這些例子也很好的詮釋了前面所學的無窮小思想。而百米起步到沖刺終點，10m跳臺起跳到剛入水，還都會一個共同的現象：運動員都做了變速直線運動，且都可以測量在某時刻運動員距離起點的位移。對此可以做出以下假設:做變速直線運動的質點的位移函數，那么該如何求質點在某時刻的瞬時速度呢？

（2）分析問題

學生對求解平均速度比較熟悉，但是對瞬時速度的求解比較陌生甚至是不會，所以要先從平均速度開始著手。變速直線運動的質點的平均速度在一般情況下不等于某時刻的瞬時速度。但是由牛頓的慣性定律可知：當時間間隔（自變量的改變量）趨于零，質點由于慣性導致它的運動狀態來不及發生變化，所以該質點在這個時間間隔內做勻速直線運動，也就是說質點在這個過程中瞬時速度等于整個過程的平均速度。所以，某個時刻的瞬時速度就等于當時間間隔（自變量的改變量）趨于零時這段時間的平均速度的極限值。

（3）建立模型

已知質點從t0運動到t時刻，在這段時間內它的平均速度

當t無限趨近于t0時，人們易知質點作勻速直線運動，所以t0時刻的瞬時速度模型為

（4）求解模型與檢驗模型

同學們在高中已經學過位移函數的導數的物理意義、簡單函數的導數公式，易知該質點在1s時的瞬時速度為v（1）=S'（1）=g*1=10m/s與采用模型(2)求解出來的結果一致，因此可知模型（2）的正確、合理性。

3.1.2 過曲線定點的切線斜率的求解

（1）提出問題

17世紀就出現了微積分，微積分是古代人類思想的巨大成果之一，是人們經過了二千余年的智慧結晶，開啟了古代數學向近代數學轉變的嶄新時代。其中萊布尼茨、牛頓功不可沒，他們分別獨立創造了微積分，單憑這一個成果，就可以確定二人在科技史上的崇高地位。但是導數的來源卻可追朔至更早的希臘時代，它的主要來源還是三個非常不同的問題:在光學傳感問題中，一般曲線的入射光是如何反射的?怎樣得知曲線運動的速度方向?以及怎樣求得兩條曲線相交時兩線構成的夾角?

但要解決三個完全不同的問題，歸根到底卻都是先要解決一個問題，那便是曲線的切線問題。如果知道了曲線C:y=f（x）上的定點M（x0，y0），求y=f（x）在點M（x0，y0）處的切線斜率。

（2）分析問題

要求解過曲線C上定點M的切線的斜率，可以先過M點做曲線的割線MN。M點固定不動，由動點N，x，y繞曲線運動，當N點沿曲線無限逼近M點時，割線MN無限接近于切線MT，也就是割線MN斜率的極限值是切線MT的斜率[3]。（如圖1所示）

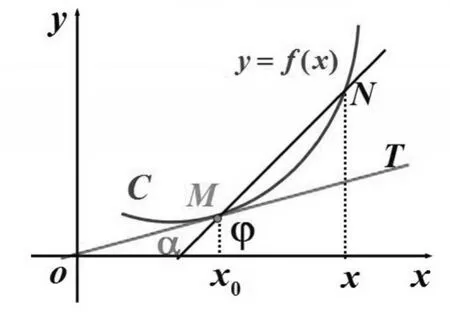
圖1 曲線過定點的割線和切線

（3）建立模型

已知，割線MN的斜率為

當N點無限趨于M點時，等價于x無限趨近于x0時，由上分析可知所求切線的斜率為

（4）求解模型與檢驗模型

舉特殊例子：設曲線C的方程為y=x2，過曲線C上的定點M（0，0）做切線，求該切線的斜率。

由模型（4）可知:

而學生在高中時曾經知道過曲線定點的切線的斜率，等于曲線方程在定點處的導值所以k切線=f'（1）=0。所以檢驗了模型（4）的合理性與可行性。

盡管這二種模式的歷史背景有所不同，但是從數學角度來說結構上是完全一樣的，都是函數值改變量與自變量改變量比值的極限，因此稱這種極限為差商的極限。

現實中，很多概念都是可以歸結為這種差商的極限，例如邊際成本等。這樣，人們就將對這類極限進行數學加工，經過抽象、總結得到了所要學習的導數定義。

3.2 導數概念

定義[3]設函數f（x）在點x0的某鄰域內有定義，若

存在時，則稱函數f（x）在一點x0處可導，則稱此極限為f（x）在該點x0處的導數，記為

由定義可得，導數值是一個差商函數的極限值。f（x）在點x0處的導數表示該極限值為給定的函數f和點x0經過差商的極限運算而誘導得到的數值，故簡稱導數。

引例1的瞬時速度可表示為S'（t0），其實際意義為物體在時刻t0的瞬時速度。

引例2的切線斜率可表示為f'（x0），其實際意義為曲線C:y=f（x）過點M（x0，y0）處的切線的斜率。

假設該極限的差商的分母為△x=x-x0（△x稱為自變量的增量），移項得x=x0+△x。又假設差商的分子是函數的增量△y=f（x）-f（x0）=f（x0+△x）-f（x0）。已知，當x→x0時，△x→0，則

這三種極限式實質上都是等差商的極限，因此都可用作導數的定義式。

由導數定義可知，可以通過公式（5）、（6）、（7）或者（8）的極限計算，如果極限存在則f（x）在點x0處可導，若極限不存在，則f（x）在點x0處不可導。

從上可以看出，求導本質上還是去極限，而且還是求差商的極限，這樣可運用前面講過的求0/0型的極限的各種技巧和方法。通過無窮小思想和極限工具，人們可以由平均速度求得瞬時速度，也由割線的斜率取極限得到切線的斜率，從而抽象詮釋為由平均變化率取極限得到變化率，最終概括總結得到了微積分的核心概念之一的導數。

4 教學總結

把數學建模的思維方式與數學文化教育方法融合于導數概念的課堂，可以使學校把傳統的接受式教學與自主學習、問題驅動和啟迪誘導相結合，調動學生積極探求新認識的愿望，學生親自感受導數概念的形成發展、抽象歸納的過程，教師指導學生正確運用數學模型剖析和解決現實問題，從而促進了學生把數學知識、數學文化教育方法和現實問題聯系一起，可以更高效地在課堂中訓練學生的數學核心素質。