論回歸性教學策略

鐘志華 李善良

摘? 要：回歸是一種十分重要的教學策略，是探明“學習者已經知道了什么”的最有效途徑. 從理論上對回歸的本質、目的、類型及基本途徑等方面進行系統探討.

關鍵詞：回歸;教學策略;認知起點

一、什么是回歸

回歸，《漢語大辭典（三）》給出的解釋是“回還，返回”. 而在西方，回歸最早來自拉丁文recurrere（跑回來），它由再次發生（recur）的詞義而來. 美國著名教育學家布魯納認為，如果沒有回歸性，任何關于思想的理論都是無用的. 一門課程在它的教學進展中，應反復地回到這些基本觀念，以這些觀念為基礎，直到學生掌握了與這些觀念相適應的完全形式的體系為止. 杜威則認為，每一個終點就是一個新的起點，每一個起點來自前一個終點. 從聯系的觀點來看，回歸，是一個尋找并識別新知識的認知起點并從中生成新知識的過程. 具體來說，它是把一個新知識或新問題放到學習者的已有知識結構之中，利用已有知識來給予表征、解釋，或讓新知識、新方法從認知起點生長出來的過程.

二、為什么要回歸

1. 回歸可以激發學生的學習興趣

長期以來，很多人對數學存在偏見，認為數學枯燥、難學. 這種錯誤的數學觀對數學教學非常有害，它像腐蝕劑一樣不斷銷蝕著學生學習數學的積極性和自信心. 數學課程標準指出，數學課堂教學的首要任務就是充分激發學生的學習興趣. 孔子認為，好學者不如樂學者. 因此，只有采取各種行之有效的方法讓抽象、枯燥的數學變得生動、有趣，學生才能好學、樂學. 而要激發學生的數學學習興趣，關鍵在于教師要將抽象的數學知識回歸具體，讓學生看得見、聽得到、摸得著，能讓學生在“做數學”的過程中充分激起探究興趣、激發數學思考、積累數學活動經驗. 只有這樣，學生的抽象才不會成為無源之水、無本之木.

例如，在講授蘇教版《普通高中課程標準實驗教科書·數學》（以下統稱“教材”）“對數的概念”這一節課時，教師將教材上的問題“某種放射性物質不斷變化為其他物質，每經過1年，這種物質剩留的質量是原來的84%，若該物質最初的質量是1，則經過[x]年該物質的剩留量為[y=0.84x]，若知道該物質的剩留量[y，]求所經歷的時間”改編成了“某種放射性物質不斷變化為其他物質，每經過1年，這種物質剩留的質量是原來的84%，若該物質最初的質量是1，同學們能提出什么問題？”這樣一個更具開放性的問題. 由于它為學生準確揭示了指數運算、冪運算及對數運算這三個概念的共同認知起點——如何從[ab=N]中知二求一？從而產生一石激起千層浪的效果，它不僅讓學生更深刻地認識到指數運算、冪運算及對數運算之間的區別與聯系，還為學生準確找到新知識產生的認知起點，讓學生在教師精心預設的教學情境中激發出主動發現問題、提出問題的強烈欲望，收到舉一反三之功效.

2. 回歸可以更好地進行數學抽象

《義務教育數學課程標準（2011年版）》指出，抽象性是數學的本質特征之一，數學在本質上研究的是抽象的東西，數學發展所依賴的最重要的基本思想也就是抽象. 但是，數學的抽象性不是憑空產生的，它需要借助一定的直觀才能達到. 數學的發展過程充分表明，數學知識的產生與發展是一個不斷從具體到抽象循環往復、不斷上升的過程. 而對數學知識的理解則需要從抽象回歸具體，要以具體作為理解的基礎，作為新知識、新思路、新方法的生長點. 這正如波利亞所言，抽象的道理是重要的，但要用一切辦法使它們看得見、摸得著，即在理解抽象的數學知識時，要通過回歸這一策略來實現從具體到抽象的升華. 我國著名數學家李大潛院士特別指出，在數學教學中，要讓抽象成為一種意識，讓探究成為一種習慣，讓回歸成為一種理念. 這不僅指明了數學學習的目標——抽象，而且進一步指明了達到這一目標的途徑與方法——探究和回歸. 因此，在數學教學中，教師不僅要善于充分利用圖形所具有的幾何直觀，將復雜的數學對象簡明化，而且要善于恰當地構造數學問題的現實情境，將抽象的數學關系具體化，還要善于通過直觀調動學生的直覺思維以獲得數學猜想，通過數形結合方法實現抽象與具體之間的轉變.

例如，在講授教材上的“導數在研究函數中的應用——單調性”這一內容時，教師播放“夜間汽車在山坡上行駛”的動畫，并提問學生：如何根據汽車的燈光來判定汽車究竟是在上坡還是下坡？這種生活化問題情境，瞬時激起了學生強烈的探究欲望，為學生深入理解運用導數研究函數的單調性奠定了良好的生活基礎，讓學生通過將山坡抽象為一條曲線，將汽車抽象為曲線上的動點，將汽車的燈光抽象為過曲線上動點的切線而很快地發現了導數與函數單調性之間的聯系.

3. 回歸可以為新知識找到生長點

眾所周知，高度的抽象性一直被認為是數學的重要特點，但現在已經逐漸演變為數學難學的代名詞. 數學固然抽象，但再抽象的數學結論總能找到相對直觀的表征和解釋. 學生之所以覺得數學抽象，最關鍵的是教師沒有為學生找到新知識賴以產生的源頭，這樣，新知識就很難從已有知識的基礎上自然而然地生長出來，于是很多教師只能把知識從外部硬塞到學生頭腦中. 由于新知識缺乏理解基礎，學生自然會覺得新知識抽象.

例如，在教學教材上的“直線與平面平行的判定定理”這一內容時，很多教師只會告訴學生如果平面外的一條直線與該平面內的一條直線平行，那么這條直線就與該平面平行，但不會給學生解釋為什么要在平面內找這樣的平行線. 由于不能真正理解知識的發生、發展過程，導致學生只能死記硬背知識點. 事實上，如果從回歸的觀點來看，線面平行的認知基礎是線線平行，注意到這一點，就比較容易理解為什么要在平面內找已知直線的平行線. 因為，兩條直線平行的實質是將一條直線平移以后能與另外一條直線重合，類比到直線與平面的平行，就是將直線適當平移以后一定能夠落在該平面內，換種說法就是在平面內存在一條直線與已知直線平行.

像這樣，在教學時如果能讓學生充分回歸到新知識產生的認知起點，并讓新知識在教師的循循善誘下從認知起點自然而然地生長出來，那么學生就不會覺得數學學習困難，也不會覺得數學學習枯燥無味. 杜威指出，有時思想的紛繁相續，常常會使思考者離開出發點十分遙遠，以致不能回溯到出發點，但細究起來，總是有一個直接經驗的情境在背后，是你所施的、所受的、所享的、所忍的，而決不單是所想的. 思維即為此情境而起. 這里的情境就是知識的生長點，讓思維回歸到知識的生長點，不僅可以使這一知識更好地固定在已經熟悉的知識點上，加強與已有知識之間的內在聯系，縮短與已有知識點之間的聯系路徑，減少信息提取的時間，有助于知識更好地被保持，還可以豐富由知識生長點所構成的概念網絡，建立更為豐富的意義家族相似網絡，從而達到深化理解之目的. 它可以避免由于思維序列過長或思維層次比較復雜而導致的思維困難. 問渠那得清如許？為有源頭活水來. 總之，只有真正找準學生的思維之源，才能充分激發學生的思維、激活學生的思路，才能在教師的精心啟發下，讓學生迸發出無窮的創造力.

4. 回歸可以促進知識的深度理解

眾里尋他千百度，驀然回首，那人卻在燈火闌珊處. 學習數學的人常有這樣的體會，有時候遇到一個難題苦思冥想總是不得要領，但當我們跳出這個問題回歸到這個問題產生的源頭時卻會豁然開朗. 之所以會出現這樣的現象，是因為：一方面，問題的源頭盡管比較簡單，但卻蘊含了理解新知識的鑰匙和解決復雜問題所需要的基本思想方法;另一方面，問題的源頭可以讓解題者去除遮蔽、返璞歸真，真正把握問題的本質，促進深度理解. 斯萊爾馬赫認為，只有返回到思想產生的根源，這些思想才可能得到真正的理解. 人工智能理論認為，深度學習是通過組合低層特征形成更加抽象的高層特征的過程. 這說明，要深度理解抽象的數學知識必須先回歸到這些知識產生的源頭.

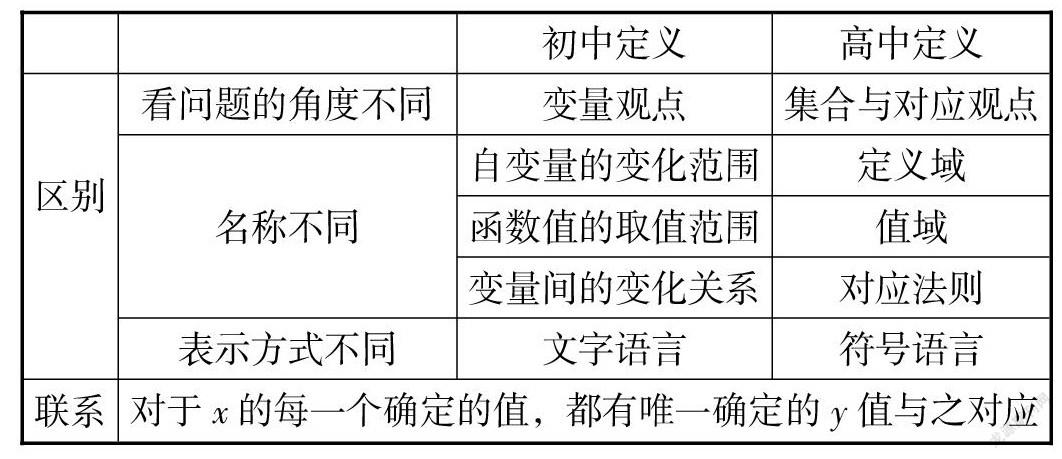
例如，很多高中生在剛學習函數的對應定義時經常有這樣的困惑：既然初中已經學過函數，為什么高中還要再學？初、高中函數定義之間到底存在什么區別與聯系？如果學生不能真正弄清這些問題，那么他們不僅很難真正理解高中函數概念的本質，而且還常常會混淆初、高中函數定義. 而解決這一問題的有效策略是采用HPM教學法，讓學生充分回歸函數概念的起源與發展歷史，讓學生認識到初中函數定義存在不完善之處，如變量的變化范圍不明確、缺乏嚴格的數學符號語言等，而高中函數定義正是為了解決初中函數定義的不完善之處而引入的，并在此基礎上進一步認識到初中函數定義與高中函數定義之間的區別與聯系（見下表），避免初中函數定義對高中函數定義的負遷移，從而讓學生真正認識到高中函數定義由于建立在集合理論基礎上而變得嚴格這一數學本質.

5. 回歸也是一種重要的解題策略

眾所周知，解決問題時既可以從已知出發向目標前進，也可以反其道而行之，從要達到的目標出發，思考達到目標應具備什么條件，已知條件是否支持這些條件？這種思想方法在數學解題中的應用十分普遍，我們在數學解題中常用的分析法、倒推法、以退為進法、特殊化法等本質上就是一種回歸方法. 著名數學家華羅庚曾經指出，要善于退，足夠地退，退到最原始而不失重要的地方，是學好數學的一個訣竅. 又說，先足夠地退到我們最容易看清楚的地方，認透了，鉆深了，然后由此向前推進. 這充分說明回歸思想在數學解題中的重要性.

例如，在解決“已知正數[a，b，c]滿足[5c-3a≤][b≤4c-a]，[clnb≥a+clnc]，則[ba]的取值范圍? ? ? ”（2012年江蘇卷理科第14題）這道題時，如果采用回歸方法，通過作變量代換[bc=x]，[ac=y]，將已知條件中的字母[c]消去，并將原問題轉化為“已知[x，y]均為正數，且滿足[5-3y≤][x≤4-y]，[lnx≥y]，求[xy]的取值范圍”這樣一個常規問題，則不僅可以促進學生深刻把握問題本質，而且可以幫助學生迅速找到解決問題的思路與方法.

三、回歸的常見類型

1. 回歸定義

這是一些有經驗的教師經常采用的一種教學策略，這種策略運用得恰到好處可以產生柳暗花明之效果. 美國著名數學家、數學教育學家波利亞在總結“回到定義”這一數學經驗時說道，回到定義去是一項重要的思維活動. 如果我們想明白為什么用文字表達的定義是如此重要，我們就應該先認識到文字是很重要的. 要是不使用文字、標記或某種符號，我們就幾乎不能應用我們的思維. 通過回到定義去，數學家尋求掌握隱藏在專業術語背后的數學對象間的真正聯系. 盡管許多教師平時也經常使用這一教學策略，但可能僅僅停留于經驗層面，然而如果能夠真正認識到這一策略的本質卻可以更加自覺、更加理性地運用它. 因為“回到定義”可以讓解題者回到知識的生長點，可以從知識的生長點去更深刻地理解問題的本質并找到解決問題的思路與方法. 回歸定義既是一種最基本的辦法，也是一種沒有辦法時的辦法. 如果在解題時，實在沒有其他辦法可用了，那么嘗試一下回歸定義，也許可以豁然開朗.

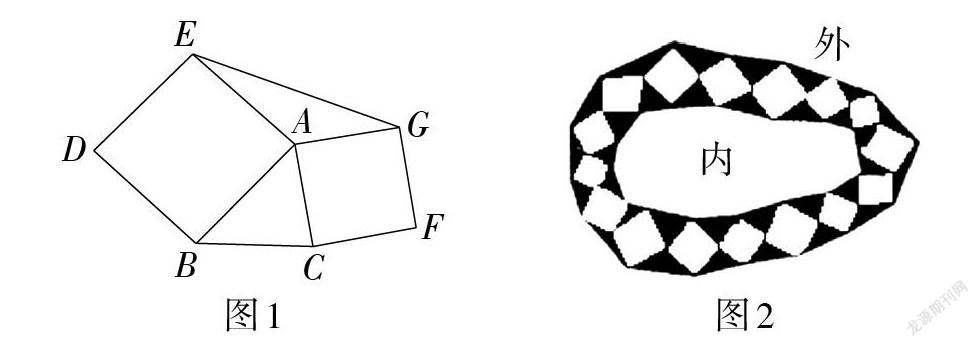
例如，（1）如圖1，分別以[△ABC]的邊[AB，AC]為邊向外作正方形[ABDE]和正方形[ACFG]，連接[EG]，試判斷[△ABC]與[△AEG]之間的關系，并說明理由.

（2）園林小路，曲徑通幽，如圖2，小路由白色的正方形大理石和黑色的三角形大理石鋪成. 已知中間的所有正方形的面積之和是[a]平方米，內圈的所有三角形的面積之和是[b]平方米，這條小路一共占地多少平方米？

對于剛學習全等三角形證明的學生來說，第（1）小題的困難是可想而知的，因為它不僅需要學生從直觀上猜想[S△ABC=S△AEG]，而且還需要采用非常規的方法證明這兩個三角形面積相等. 許多學生盡管能夠猜想出[S△ABC=S△AEG]，但卻不知道如何去證明這一結論. 這時，回歸定義的“威力”就顯現出來了，因為要證明這兩個三角形面積相等，首先需要將這兩個三角形的面積表示出來，而要表示就需要用到三角形面積的定義. 當然，在運用定義的過程中需要具有一定的靈活性，許多學生一開始會受圖形條件的干擾去作線段[BC]和[EG]的高，但最后卻無功而返，因為既無法證明[BC=EG]，也無法證明其邊上的高相等. 這就需要結合具體圖形靈活運用回歸定義方法. 事實上，只要注意到[△ABC]與[△AEG]有一條邊相等（[AC=AG]），就容易想到分別作[AC，AG]邊上的高[BQ，EP]，然后再證明[BQ=EP]，如圖3所示.

至于第（2）小題的求解，可以通過回歸第（1）小題而獲得解決.

需要注意的是，在數學教學中，許多學生常常會因為枯燥無味、考試不考而忽視定義的價值. 其實，在思路的探求、方法的產生及問題的轉化等方面，定義有著其他方法無法取代的作用. 因此，在實際教學中，教師要牢牢抓住定義并引導學生及時回歸定義，這樣既能幫助學生鞏固所學，又能充分激發學生的思維，促進數學問題的順利解決.

2. 回歸原型

心理學認為，原型（Prototype）不是某一個特定對象的內部復本，而是一類客體的內部表征，它反映一類客體具有的基本特征，原型的最大特點是它能較其他樣例更容易發現這類模式的本質特征. 事實上，無論一個問題多么復雜，它都是簡單問題通過多次變式以后得到的，我們總可以從中找到構成復雜問題的基本要素——原型. 數學的基礎知識、基本技能、基本活動經驗及基本思想方法中有很多都可以作為解決復雜問題的原型，如勾股定理是余弦定理、兩點間的距離公式、點到直線的距離公式等諸多數學公式的原型;拋硬幣、擲骰子的經驗是理解許多概率問題的基礎——活動經驗原型;化歸方法、數形結合思想方法是解決許多數學問題的方法原型. 因此，在數學學習中，我們應該善于識別復雜問題中的原型，并及時將復雜問題轉化為基本問題——原型，然后再從基本問題（原型）中找到解決復雜問題的思路與方法.

例如，對于題目“在[△ABC]中，已知[∠ACB=90°]，[AC=2，BC=23，E，F]是邊[AB]上異于[A，B]的兩點，[EF=1]，如圖4所示. 求[CE · CF]的范圍”，如果采用常規方法（建立平面直角坐標系）求解，費時費力. 但是如果解題者知道極化恒等式[a · b=14a+b2-a-b2]這一原型，那么求解就變得非常容易. 事實上，令[M]為[EF]的中點，則有[CE · CF=14CE+CF2-CE-CF2=][142CM2-EF2=CM2-14]. 這樣，只需要求出[CM2]的取值范圍即可.

極化恒等式不僅在解決很多數學問題時非常有效，而且在數學發展史上也有重要地位. 在對數產生以前，人們為了解決生產實際中出現的大量計算問題，常常利用極化恒等式將兩個大數的乘積先表示為這兩個數的平方和與這兩個數的平方差之差的四分之一，然后再通過查平方表進行計算. 在近幾年的高考試題中，也經常會見到極化恒等式的影子.

例如，對于下面兩道高考試題，如果采用極化恒等式解題就非常簡便.

（2010年福建卷文科第11題）若點[O]和點[F]分別為橢圓[x24+y23=1]的中心和左焦點，點[P]為橢圓上的任意一點，則[OP · FP]的最大值為（? ? ）.

（A）2? ? （B）3? ? ?（C）6? ? ?（D）8

（2017年全國Ⅱ卷理科第12題）已知[△ABC]是邊長為2的等邊三角形，[P]為平面[ABC]內一點，則[PA · PB+PC]的最小值是（? ? ）.

（A）-2? ?（B）[-32]? ?（C）[-43]? ?（D）-1

3. 回到核心觀點和核心概念

約翰·D.布蘭思福特和安·L.布朗等人在研究中發現，專家的知識不僅僅是對相關領域的事實和公式的簡單羅列，相反它是圍繞核心概念或“大觀點”（big idea）來組織的，這些概念和觀點引導他們去思考自己的領域. 根據這一研究，他提出教學要圍繞“大概念”或“大觀點”來聯系和組織……有效的學習要求教師必須了解他們所教學科的結構（貫穿于其中的思想），并以此作為認知路標來指導學生的作業，來評價學生的進步. 這一研究結果與上面所提到的回歸性策略不謀而合，回歸的目的是回到知識產生的生長點，并從此出發產生和發現新的知識. 而核心概念和“大觀點”正是新知識得以產生的重要生長點，回歸到核心概念或“大觀點”是為了更好地促進知識的發生和生長.

下面以“一元微積分”的教學為例來具體說明如何圍繞核心概念或“大觀點”來建構數學知識體系，如圖5所示.

①→②，極限概念起源于函數概念，它研究的是函數的自變量在一個無限變化過程中因變量變化的趨勢，屬于函數性質方面的內容.

②→①，從極限返回研究函數. 一方面，可以借助極限定義的概念——連續來對函數進行重新分類，即把函數分成連續函數與非連續函數;另一方面，可以利用極限更加深入地研究函數的圖象與性質，如通過研究函數圖象的漸近線可以更好地了解函數圖象無限伸展的趨勢.

②→③④，既是極限概念的進一步深化與應用，也是函數性質的進一步拓廣.

③→①，利用導數返回研究函數. 這不僅可以更好地了解函數的本質，如可以利用導數求函數的極值點、拐點、漸近線，求曲線的切線和法線等，而且可以更好地了解函數圖象的性態，如可導函數在作圖時只要用平滑的曲線把有限個點連接起來就可以基本反映圖象的大體形狀.

③→②，利用導數可以研究函數的極限，如利用洛必達法則求不定式極限，利用泰勒公式求極限等，這讓極限計算如虎添翼.

③→④，主要解決如何求一個函數原函數的問題，它是導數運算的逆運算.

④→①，利用積分返回研究函數，可以進一步深化對函數本質的認識，如可以求封閉曲線所圍圖形的面積、可以討論函數的可積性等，而變上限函數的出現則進一步開闊了我們對函數的認識.

④→②，由定積分可以研究函數的極限，如用定積分定義求數列極限等.

④→③，不僅可以更好地認識導數與積分之間的關系，而且利用導數可以更好地解決定積分的計算問題. 利用變上限函數的導數推得的牛頓-萊布尼茲公式不僅把定積分與不定積分有機聯系起來，而且簡化了定積分的計算.

由圖5可以看出，一方面，一元函數微積分學的7個基本概念——函數、極限、連續、導數、微分、不定積分、定積分（函數概念除外）都可以從函數這一核心概念生成，如導數是函數增量比極限，定積分是函數積分和極限等;另一方面，通過回歸式教學又可以對函數進行分類，可以研究函數的連續性、單調性、最值、極值等各種性質，從而促進對函數的深度理解. 這樣，上面的7個基本概念（函數概念除外）都可以統一在函數這一核心概念之下，一元微積分學最終歸結為利用極限研究一元函數的學問.

4. 回歸生活

數學來自生活，生活中處處包含著數學. 著名教育家陶行知先生曾說過，生活教育是給生活以教育，用生活來教育，為生活的向上、向前的需要而教育. 數學存在于我們生活的方方面面，在平時，教師應處處留心生活情境，觀察生活事實，挖掘潛藏在生活現象背后的數學知識，并將其帶入數學課堂.

生活點滴不僅是學生學習的助力點，也是教師創設生活情境的借力點. 隨著課程改革的逐步實施，“滿堂灌”在數學課堂中日漸式微，現在的數學課堂更強調學生的自主探索，而這需要教師創設具有豐富生活背景的數學情境來引發學生發現、提出問題，進而分析與解決問題. 因此，教師應注重觀察生活點滴、積累生活經驗，在數學教學中以生活原型為背景，讓學生充分回歸生活，在生活中“找”數學，“想”數學. 例如，有的教師在講授“確定圓的條件”這一內容時就針對學生畫圓不完整這一普遍現象創設了這樣一種教學情境：教師在黑板上畫圓時由于不小心手抖了一下，圓心找不到了，怎樣才能把剩下的部分畫完？然后自然而然想到在已有的圓弧上取一點、兩點直至三點才能確定圓心. 學生十分熟悉這一情境，不僅容易引起學生的共鳴，而且能充分激發學生的探究欲望.

四、回歸的基本途徑

1. 善于進行新、舊聯想

回歸，是一個尋找并識別新知識的認知起點的過程. 因此，進行回歸時要先努力尋求所學的新知識或面臨的新問題與學習者頭腦中已有知識之間的聯系，然后思考是否可以利用已有知識來表征或解釋這些新知識或新問題. 在這方面，波利亞曾經提出了許多好的策略，他指出，遇到一個新問題時，首先要思考：這是什么類型的問題？你以前見過它嗎？它與某個已知的問題有關嗎？它像某個已知問題嗎？你見過同樣的題目以一種不同的形式出現嗎？你見過一個類似的問題嗎？你見過一個條件類似、結論類似、圖形類似或方法類似的問題嗎？你見過一個更特殊的問題嗎？你見過一個更一般的問題嗎？例如，在教學“簡單的線性規劃”這一新知識時，教師就可以將其與“二元一次不等式（組）與平面區域”“一元函數的最值問題”“特殊二元函數的最值問題”“向量的數量積”等諸多知識建立聯系.

2. 準確識別認知起點

奧蘇貝爾在其名著《教育心理學——認知觀點》的扉頁上這樣寫道：“假如讓我把全部教育心理學僅僅歸結為一條原理的話，那么，我將一言以蔽之曰：影響學習的唯一重要的因素，就是學習者已經知道了什么. 要探明這一點，并應據此進行教學.”這說明，只有準確地把握認知起點，才能為新知識的學習找到生長點和固著點，才能更好地認識新知識的本質，新知識才能學得深、記得牢.

例如，在解決“求[z=2x+3y]的最大值，使[x，y]滿足約束條件[x+2y≤8，x≤4，y≤3，x≥0，y≥0]”這一問題時，如果將“一元函數的最值問題”或“特殊二元函數的最值問題”作為認知起點，就不僅可以使學生更加深刻地認識到該問題是“求二元函數最值問題”這一實質，而且可以從學生熟悉的知識入手，通過類比自然而然找到解決問題的方法.

3. 巧用啟發理解新知

回歸不是目的，而是為了更好地前進. 找到了新知識的認知起點和新、舊知識之間的聯系僅完成了回歸的第一步，只有把認知起點作為新知識的生長點或新思想的生發點，并靈活運用各種啟發策略讓學生從這些認知起點出發生成新知識、新思想、新方法，才算真正達到了回歸的目的.

例如，在解決問題時，教師可以這樣啟發學生：我們以前有沒有遇到過這類問題？如果學生回答“沒有”，教師就可以進一步啟發學生：我們以前有沒有遇到過類似問題？提出這一問題的目的是引導學生回憶過去所學過的特殊二元函數的最值問題（如“已知函數[x，y]滿足等式[x-22+y2=3]，求[yx]的最大值”等），如果學生能夠回憶起以前所學過的特殊二元函數的最值問題，教師就可以進一步追問學生：我們當時是怎么解決這一問題的？其中的數學思想方法是什么？提出這兩個問題的目的：一是讓學生認識到解決這一問題的關鍵是找到目標函數[yx]的幾何意義，并把它轉化為一元函數的最值問題;二是為即將解決的線性規劃問題找到類比對象和新方法的生長點. 當學生把這些問題弄清楚以后，教師可以順勢提問學生：這與我們現在要求的問題有什么關系？你能從中獲得什么啟發？提出這兩個問題的目的：一方面，要讓學生認識到這兩類問題之間具有特殊與一般的關系，并啟發學生類比舊問題解決新問題;另一方面，希望將學生的思維導向求二元函數最值問題的關鍵——找出目標函數的幾何意義，并將二元函數最值問題轉化為一元函數最值問題. 如果學生能認識到這一點，教師就可以很自然地提出“你能說出表達式[2x+3y]的幾何意義嗎？”“看到[2x+3y]，你能聯想到什么？”等問題，通過這樣的啟發讓學生自然地將[2x+3y]與兩個向量[x，y]，[2，3]的數量積聯系起來，進而認識到表達式[2x+3y]的幾何意義就是動向量[x，y]在定向量[2，3]上的投影與定向量[2，3]的長度的乘積，從而將求目標函數[z=2x+3y]這一二元函數的最值問題成功轉化為求動向量[x，y]在定向量[2，3]上的投影這一一元函數的最值問題.

參考文獻：

[1]小威廉姆，E.多爾. 后現代課程觀[M]. 王紅宇，譯. 北京：教育科學出版社，2003.

[2]JEROME BRUNER. Actual Minds，Possible Worlds[M]. Cambridge MA：Harvard University Press，1986.

[3]布魯納. 教育過程[M]. 邵瑞珍，譯. 北京：文化教育出版社，1982.

[4]張萍.“對數的概念”教學設計[J]. 數學通報，2014，53（4）：28-30，33.

[5]中華人民共和國教育部制定. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.

[6]秦霞，鐘志華. 生活中抽象，合作中探究，數學中回歸：“導數在研究函數中的應用——單調性”教學實踐與評析[J]. 教育研究與評論（中學教育教學版），2016（1）：75-82.

[7]約翰·杜威. 思維與教學[M]. 孟獻承，俞慶堂，譯. 上海：商務印書館，1936.

[8]漢斯-格奧爾格·加達默爾. 真理與方法[M]. 洪漢鼎，譯. 上海：上海譯文出版社，2005.

[9]波利亞. 怎樣解題[M]. 涂泓，馮承天，譯. 上海：上海科技教育出版社，2004.

[10]王甦，汪安圣. 認知心理學[M]. 北京：北京大學出版社，2004.

[11]張玉虎. 一個活躍在高考中的恒等式[J]. 中學數學月刊，2020（4）：56-57.

[12]約翰·D.布蘭思福特，安·L.布朗，羅德尼·R.科金，等. 人是如何學習的：大腦、心理、經驗及學校[M]. 程可拉，孫亞玲，王旭卿，譯. 上海：華東師范大學出版社，2003.

[13]潘書林. 返回式框圖學習法[J]. 數學教育學報，2001，5（2）：36-37.