基于寬頻阻抗譜技術的XLPE電纜老化診斷方法研究

單秉亮，李舒寧，孫茂倫，杜承謙，王 偉，李成榕，孟曉凱

（1.新能源電力系統國家重點實驗室（華北電力大學），北京 102206；2.國網山西省電力公司電力科學研究院，山西 太原 030001）

0 引言

交聯聚乙烯（XLPE）電力電纜以其良好的絕緣性能和耐熱性能，廣泛應用于我國城市電網的建設與改造。作為城市電能傳輸和分配的主要設備，其運行狀況及可靠性直接關系到整個電網系統的安全與穩定。截至目前，我國XLPE電纜大規模入地接近20年，已逐步進入“老齡化”階段，部分在役電纜正接近或已超過其設計壽命，由此帶來的電纜本體絕緣老化問題正日益威脅著電網的運行安全[1]。因此，及時、準確掌握電纜本體絕緣老化狀態，并據此開展合理的狀態檢修顯得愈發重要[2-3]。

目前研究相對成熟且可用于現場電纜老化診斷的技術相對較少，主要以取樣分析技術和0.1 Hz超低頻介損檢測技術為代表[4]。前者可用于評估電纜發生的熱老化、水樹老化等，后者則更傾向于診斷電纜中的水樹老化[5-7]。然而，取樣分析技術在現場應用時具有破壞性，僅適用于取樣成本相對較低、整體近似呈均勻老化配電電纜的老化診斷[5-6]；0.1 Hz超低頻介損檢測技術雖然已被列為電纜現場試驗內容之一，但其能否與工頻介損檢測完全等效并反映工頻下運行電纜的絕緣狀態仍需進一步研究，且施加的高達1.5U0的0.1 Hz超低頻電壓也有可能激發電纜中潛在的絕緣缺陷并造成二次傷害[7]。在此情況下，探索新型電纜老化診斷方法，有利于加快解決我國存在的大規模電纜老化問題，相關研究工作刻不容緩。

近年來，以寬頻阻抗譜（broadband impedance spectroscopy，BIS）[8-10]和反射系數譜（reflection coefficient spectroscopy，RCS）[11]為代表的頻域反射（frequency domain reflectometry，FDR）技術被國內外學者用于研究電力電纜中的缺陷定位。相較傳統時域反射（time domain reflectometry，TDR）技術而言，FDR技術的測量信號中含有更多的高頻成分，對于電纜電氣參數變化較小的本體老化缺陷也具有較高靈敏度[12]。然而，現有研究中該技術主要用于電纜中的缺陷定位，基于其診斷電纜本體絕緣老化的研究相對較少。

鑒于此，本文深入研究BIS技術，提出利用電纜輸入阻抗譜計算電纜中波速并據此診斷XLPE電纜絕緣老化的方法，并通過仿真和試驗研究論證該診斷方法的有效性。

1 電纜波速診斷絕緣老化的依據及其計算方法

1.1 診斷依據

以圖1所示的單芯10 kV XLPE電纜為例，分析電纜老化對高頻電磁波在電纜中傳播速度的影響。

由圖1可知，XLPE電纜絕緣結構主要由XLPE絕緣層和內、外半導電層共同構成，因此電纜絕緣結構等效電容Cequal可按式（1）計算。

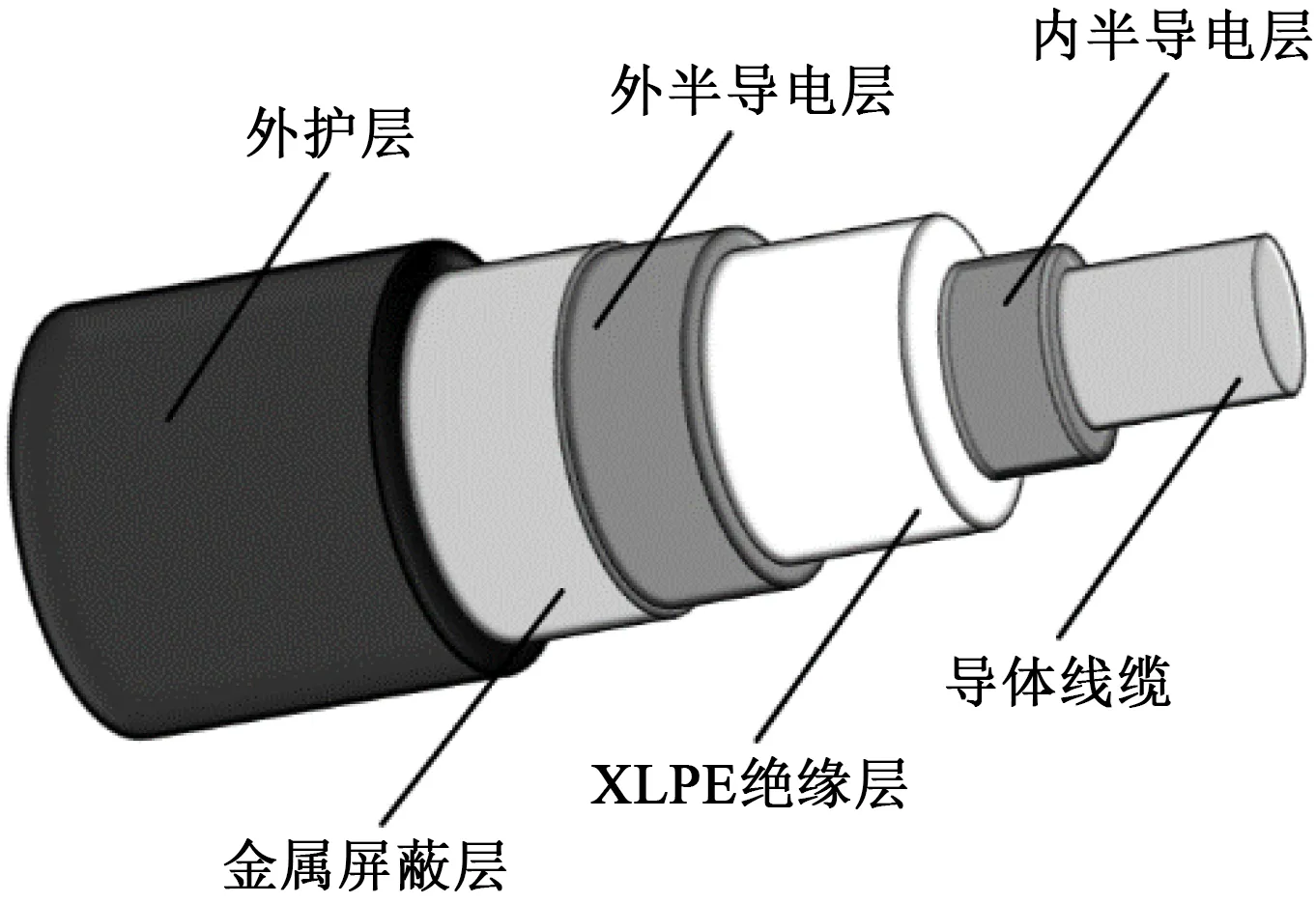
圖1 XLPE電纜結構示意圖Fig.1 Structure diagram of XLPE cables

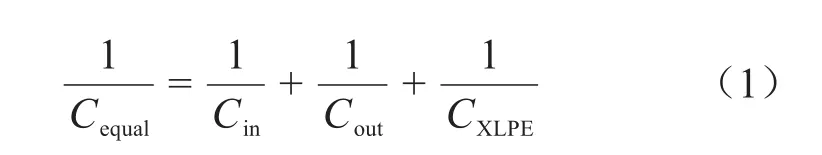
式（1）中：CXLPE表示電纜XLPE層的電容值；Cin、Cout分別表示電纜內、外半導電層的電容值。XLPE電纜在實際運行過程中，其絕緣層會在電、熱、機械、環境等因素作用下發生老化，進而影響電纜絕緣結構的介電特性。

水樹老化和熱老化是運行電纜絕緣主要的老化形式，電纜發生水樹老化時，其XLPE絕緣層中的內部極性基團及空間電荷數量會明顯增多，相應的松弛極化過程也會顯著增強；電纜發生熱老化時，XLPE分子鏈會發生斷裂繼而形成低分子產物，這在一定程度上可以加劇界面極化，上述過程均會引起XLPE絕緣層相對介電常數的增大[13-14]。與此同時，由于材料電容值和其相對介電常數正相關，XLPE絕緣層電容值也會隨之變大。假設電纜老化過程中其內外半導電層的相對介電常數（或電容）基本保持不變，則根據式（1）可知，老化電纜XLPE絕緣層電容值的提高會導致絕緣結構整體等效電容Cequal的增大，這在一定程度上意味著電纜絕緣結構整體等效相對介電常數也隨之增大。而對于XLPE電纜而言，高頻電磁波在其內部的傳播速度v與頻率基本無關，可表示為式（2）[15]。

式（2）中：c0為電磁波在真空中的波速；εr和μr分別表示介質的相對介電常數和相對磁導率。

鑒于前文已闡述電纜老化后其整體等效相對介電常數會有所提高，結合式（2）可以看出，等效相對介電常數的提高最終會導致波速v降低。因此，電纜老化會導致波速v發生改變，可據此開展電纜老化診斷工作。

1.2 基于輸入阻抗譜的電纜波速計算方法

長度為l的電纜末端開路時的輸入阻抗幅值頻譜Z|in|可表示為式（3）[16]。

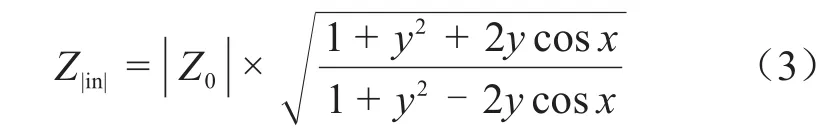
式（3）中：Z0為電纜的特征阻抗；x=-2βl，y=e-2αl，其中α和β分別為電纜的衰減系數和相位系數。鑒于高頻下電纜Z0取值近似為常數[17]、y恒為正值，當且僅當cosx=1時，Z|in|會取極大值。此時，x=-2βl=2kπ，其中k為整數。

與此同時，β可表示為式（4）。

式（4）中：f為信號的頻率；ν為電纜中波速。因此電纜輸入阻抗幅值的極大值出現的頻率為式（5）。

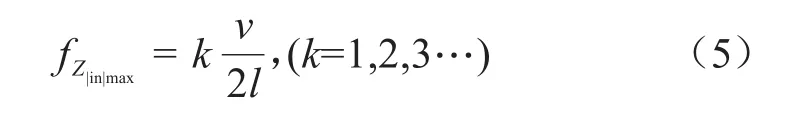
設fn+1和fn分別為電纜輸入阻抗幅值第（n+1）和第n個極大值所對應的頻率，n為非負整數。則電纜波速ν可表示為式（6）。

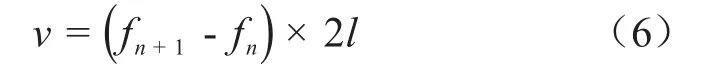
需說明的是，對于均勻老化電纜而言，式（6）求得的波速ν代表電纜中任意位置的波速；對于分段老化電纜而言，根據式（6）計算的波速實際上為電纜中的平均波速[18]。

2 仿真研究

2.1 仿真參數

文獻[16,19]對10 kV XLPE電纜絕緣結構（包括XLPE絕緣層及內、外半導電層）在不同熱老化情況下的頻域介電響應特性進行了測量。鑒于在103～109Hz頻率范圍內XLPE的極化過程主要以偶極子的轉向極化為主[20]，文獻[16]基于Cole-Cole模型利用式（7）來擬合10 kHz～100 MHz內XLPE電纜絕緣結構的復介電常數變化過程。

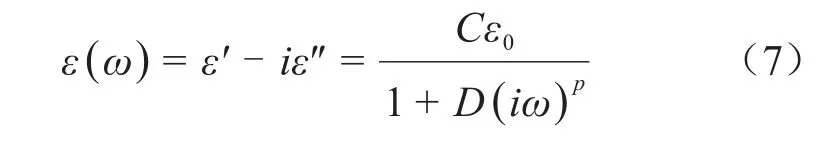
式（7）中：ε′和ε″分別為介質介電常數的實部和虛部；C、D和P為擬合系數；ε0為真空的介電常數；ω為角頻率。擬合后不同熱老化程度下XLPE電纜絕緣復介電常數擬合參數值如表1[16]所示。本研究在仿真過程中，通過改變電纜不同位置絕緣復介電常數擬合參數值即可模擬不同老化程度及老化區域分布的電纜。此外，仿真過程中電纜金屬導體半徑為10 mm，電纜絕緣厚度為5.5 mm，金屬屏蔽層厚度為0.2 mm。

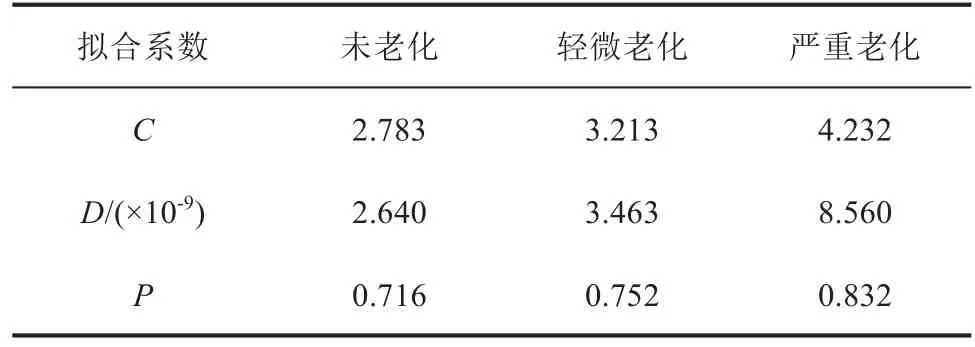
表1 不同熱老化電纜絕緣復介電常數擬合參數值Tab.1 Fitting parameters of complex dielectric constants of different thermal ageing cable insulations

2.2 電纜均勻老化診斷仿真研究

2.2.1 老化程度對波速的影響

以100 m長的單芯10 kV XLPE電纜為例，仿真電纜在整體未老化、均勻輕微老化和均勻嚴重老化3種情況下末端開路時的輸入阻抗幅值頻譜，結果如圖2所示。從圖2可以看出，不同老化程度電纜的輸入阻抗幅值頻譜存在明顯差異，電纜老化越嚴重，其阻抗幅值頻譜相鄰極大值對應的頻率間隔越小。

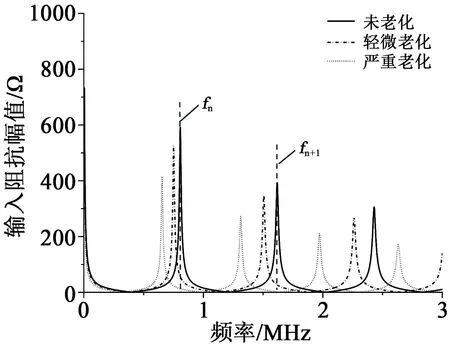
圖2 不同程度均勻老化電纜的輸入阻抗幅值頻譜Fig.2 Input impedance amplitude spectra of uniform ageing cables with different ageing degrees

結合式（6）計算電纜各老化程度下的波速，結果對比如圖3所示。從圖3可以看出，整體未老化、均勻輕微老化和均勻嚴重老化3種情況下電纜中波速分別為162、151、132 m/μs，不同老化程度電纜的波速差異較大，電纜的老化程度與波速確實存在明顯的對應關系。電纜老化越嚴重，對應的波速越小，例如當電纜發生嚴重老化時，其波速相較未老化時下降了18.5%，變化幅度較為明顯。上述規律與1.1中的理論依據分析相一致，因此，電纜中波速具有診斷均勻老化電纜老化狀況的潛力。

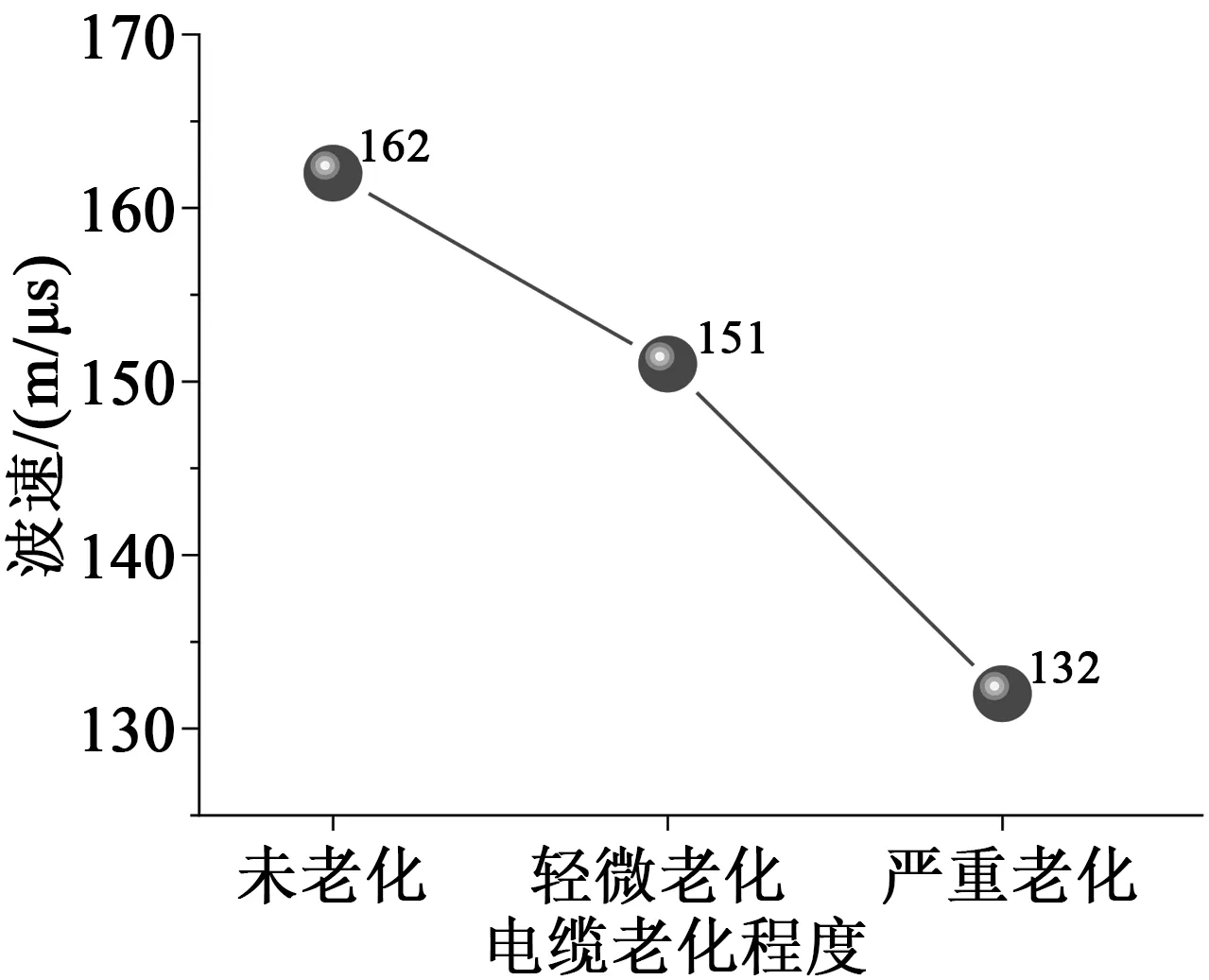
圖3 均勻老化電纜波速和老化程度的關系Fig.3 Correlation between wave velocity and ageing degree of uniform ageing cables

2.2.2 電纜長度對波速的影響

實際運行電纜長度不一，為研究基于輸入阻抗譜計算不同長度電纜中波速的穩定性，本研究進一步仿真了10 m、1 000 m兩種長度電纜在整體發生均勻老化和未老化時的阻抗幅值頻譜，分別計算電纜中波速并與圖3中100 m電纜波速進行對比，結果如圖4所示。由圖4可以看出，當電纜老化狀態相同時，不同長度電纜中波速的計算值差異較小。這在一定程度上證明了基于電纜輸入阻抗譜計算電纜中波速的穩定性較好，基本不受長度的影響。

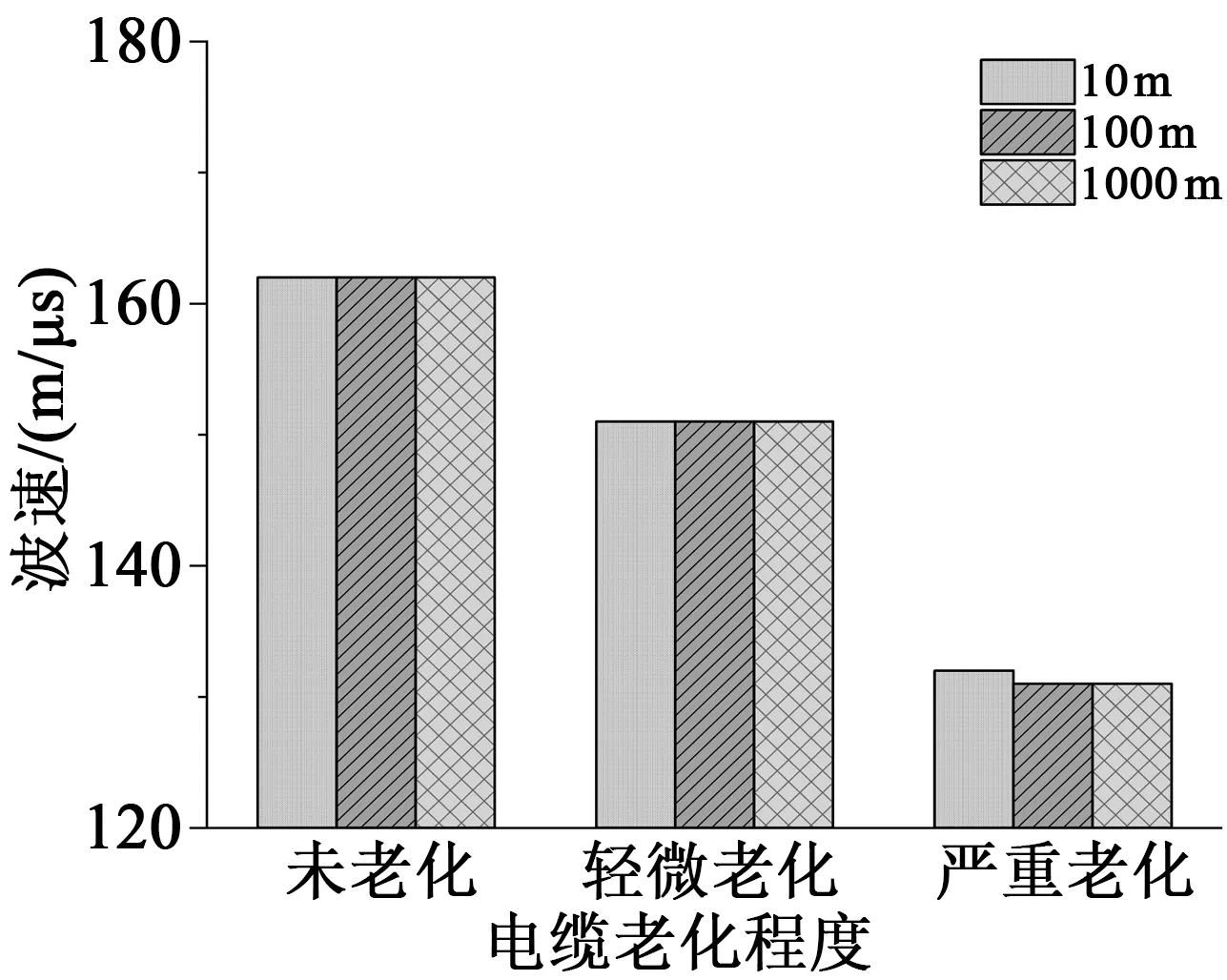
圖4 不同長度電纜中波速計算值Fig.4 Calculated values of wave velocity in cables with different lengths

2.3 電纜分段老化診斷仿真研究

由于XLPE配電電纜空間跨度大、敷設環境復雜，運行電纜分段老化現象普遍存在，如圖5所示，即電纜絕緣老化狀態沿其線路并非呈均勻分布，亟需研究電纜波速對電纜分段老化診斷的有效性。

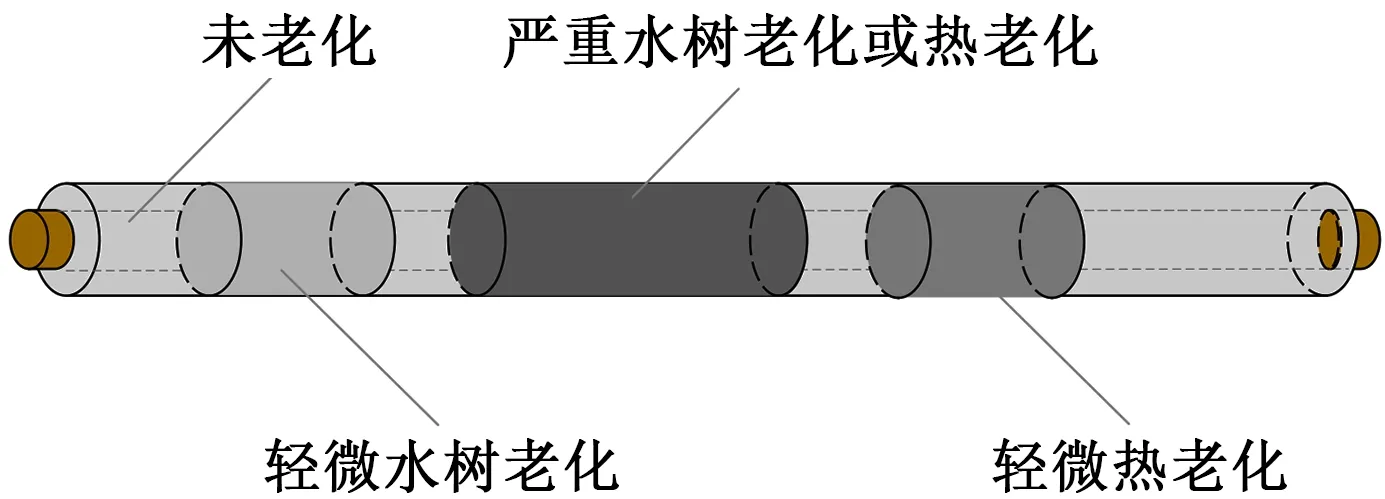
圖5 分段老化電纜示意圖Fig.5 Structure diagram of the segmented-ageing cable

2.3.1 電纜分段老化程度對平均波速的影響

首先以100 m長的單芯10 kV XLPE電纜為例，將距電纜首端20～60 m的區域設為分段老化發生位置，其他區域設為未老化區域。在電纜末端開路的條件下仿真了分段老化區域發生均勻輕微老化和均勻嚴重老化兩種情況下的首端輸入阻抗幅值頻譜，并與100 m未老化電纜的仿真結果進行對比，結果如圖6所示。從圖6可以看出，電纜發生分段老化時，其輸入阻抗幅值頻譜同樣與未老化電纜存在明顯差異。結合式（6）計算各電纜的平均波速如圖7所示。

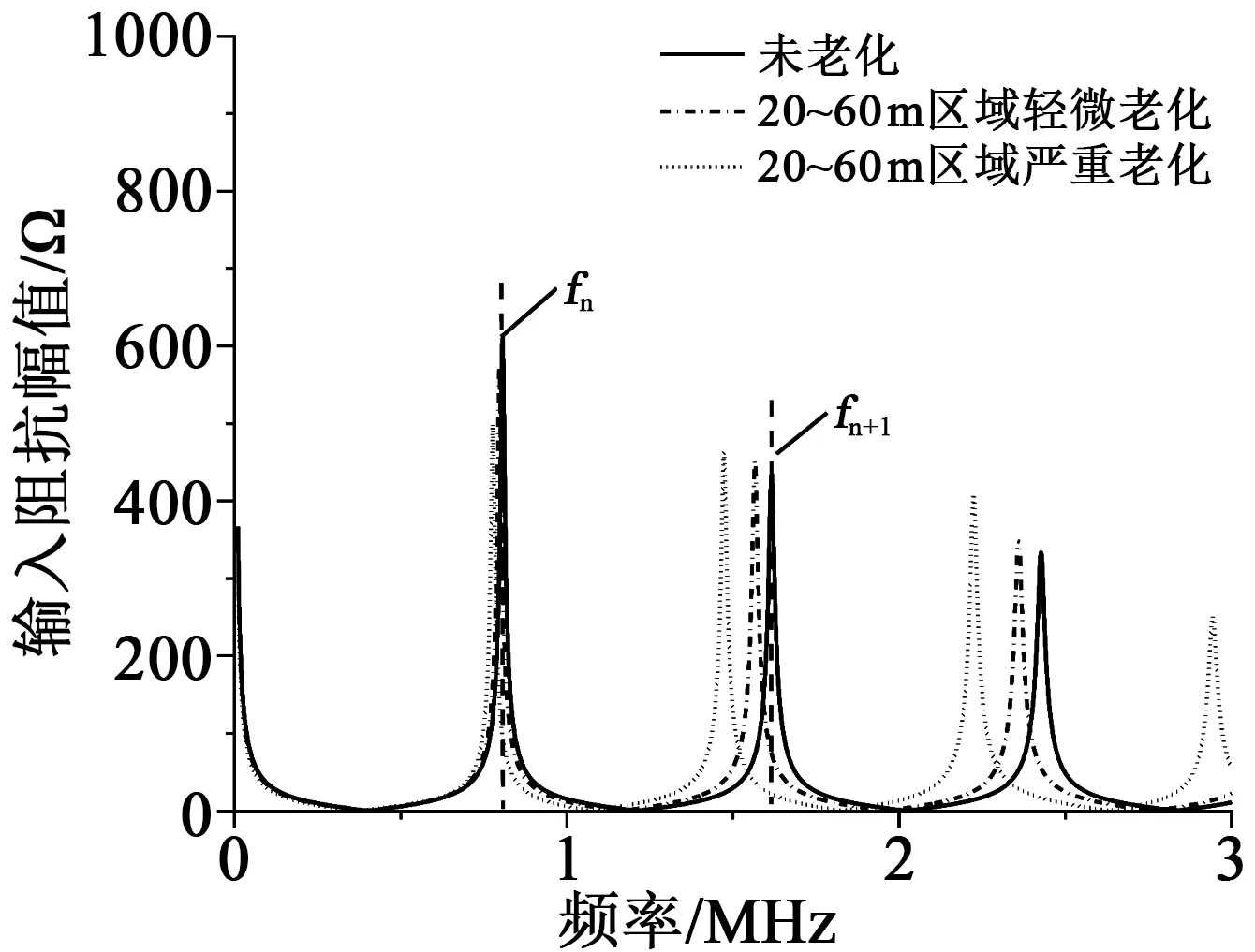
圖6 不同程度分段老化電纜的輸入阻抗幅值頻譜Fig.6 Input impedance amplitude spectra of segmentedageing cables with different ageing degrees

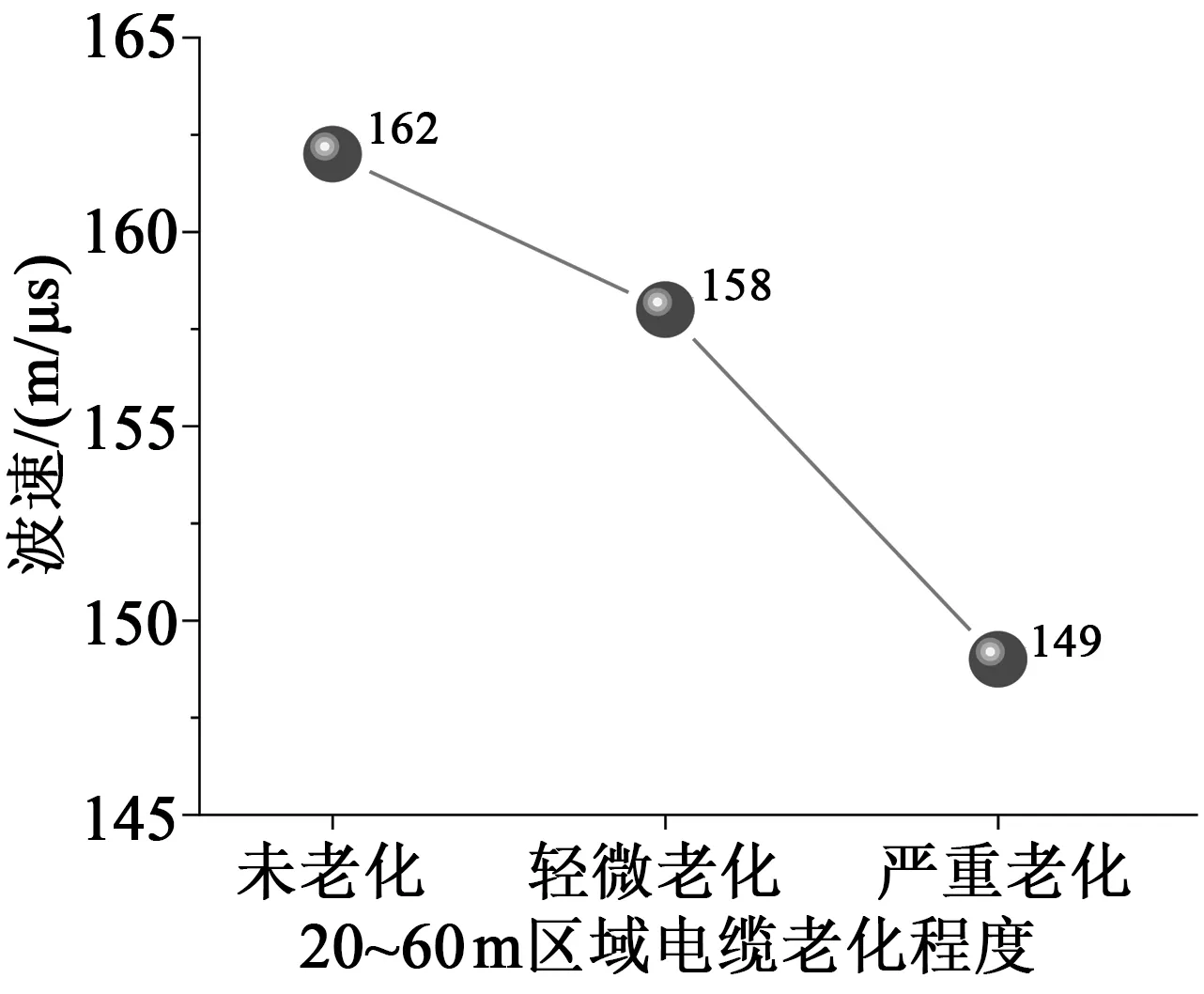
圖7 分段老化電纜平均波速和老化程度的關系Fig.7 Correlation between average wave velocity and ageing degree of segmented-ageing cables

從圖7可以看出，隨著電纜分段老化嚴重程度的增加，電纜平均波速逐漸減小。由此可見，基于輸入阻抗譜計算得到的平均波速可以有效地反映出電纜分段老化嚴重程度的變化。

2.3.2 電纜分段老化區域長度占比對平均波速的影響

在上述研究基礎上，進一步仿真研究了電纜分段老化區域不同長度占比情況下的輸入阻抗幅值頻譜，結合式（6）計算了電纜平均波速與電纜分段老化區域長度占比的關聯關系，結果如表2所示。其中，電纜分段老化發生位置區域（距電纜首端）分別為：20～21 m、20～25 m、20～30 m、20～40 m、20～60 m、20～80 m、20～100 m、0～100 m，即電纜分段老化區域占比分別為1%、5%、10%、20%、40%、60%、80%、100%。

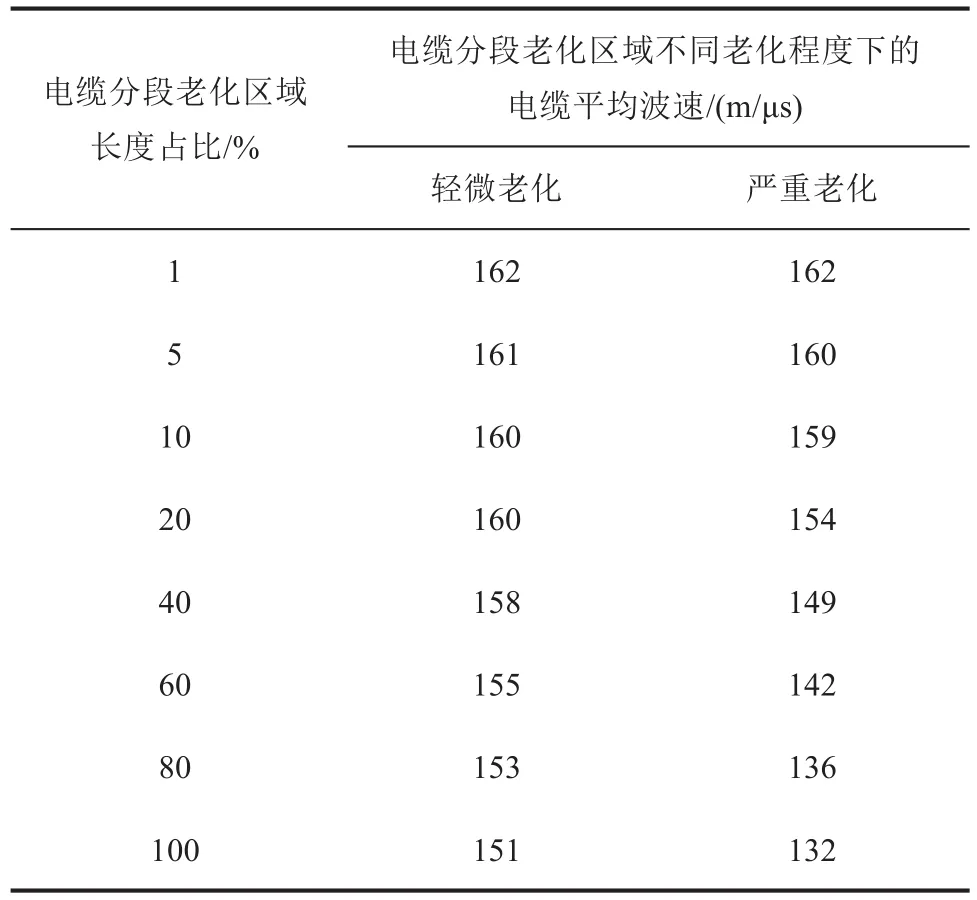
表2 分段老化電纜平均波速和老化區域長度占比的關系Tab.2 Correlation between average wave velocity and length percentage of ageing areas of segmented-ageing cables

從表2可以看出，當電纜分段老化區域老化程度相同時，分段區域長度占比越高，對應的電纜平均波速越小。當電纜分段老化區域長度占比相同時，分段老化區域老化越嚴重，電纜平均波速同樣越小。因此，基于電纜平均波速可以有效地表征電纜分段老化區域長度占比的變化。此外，可以發現，當電纜分段老化區域長度占比為1%時，電纜平均波速相較未老化電纜波速基本一致；而當電纜分段老化區域長度占比大5%時，電纜平均波速發生改變，此時電纜老化可以被有效診斷。

2.3.3 電纜分段老化發生位置對平均波速的影響

由于電纜絕緣老化過程受敷設環境因素影響較大，電纜分段老化發生位置并非固定。但在評價電纜絕緣老化狀態時所選取的表征量不應受電纜分段老化發生位置的影響。同樣以100 m長的單芯10 kV XLPE電纜為例，仿真電纜分段老化總長度同為40 m，分段老化程度及發生位置不同時的電纜輸入阻抗譜，并據此計算各老化情況下的電纜平均波速結果如圖8所示。其中，電纜分段老化發生位置區域如下：①距電纜首端10～30 m和50～70 m；②距電纜首端20～60 m；③距電纜首端30～70 m；④距電纜首端40～80 m；⑤距電纜首端20～40 m和60～80 m。從圖8可以看出，當電纜分段老化長度占比相同時，電纜平均波速只與電纜分段老化嚴重程度相關，基本不受電纜分段老化發生位置的影響。

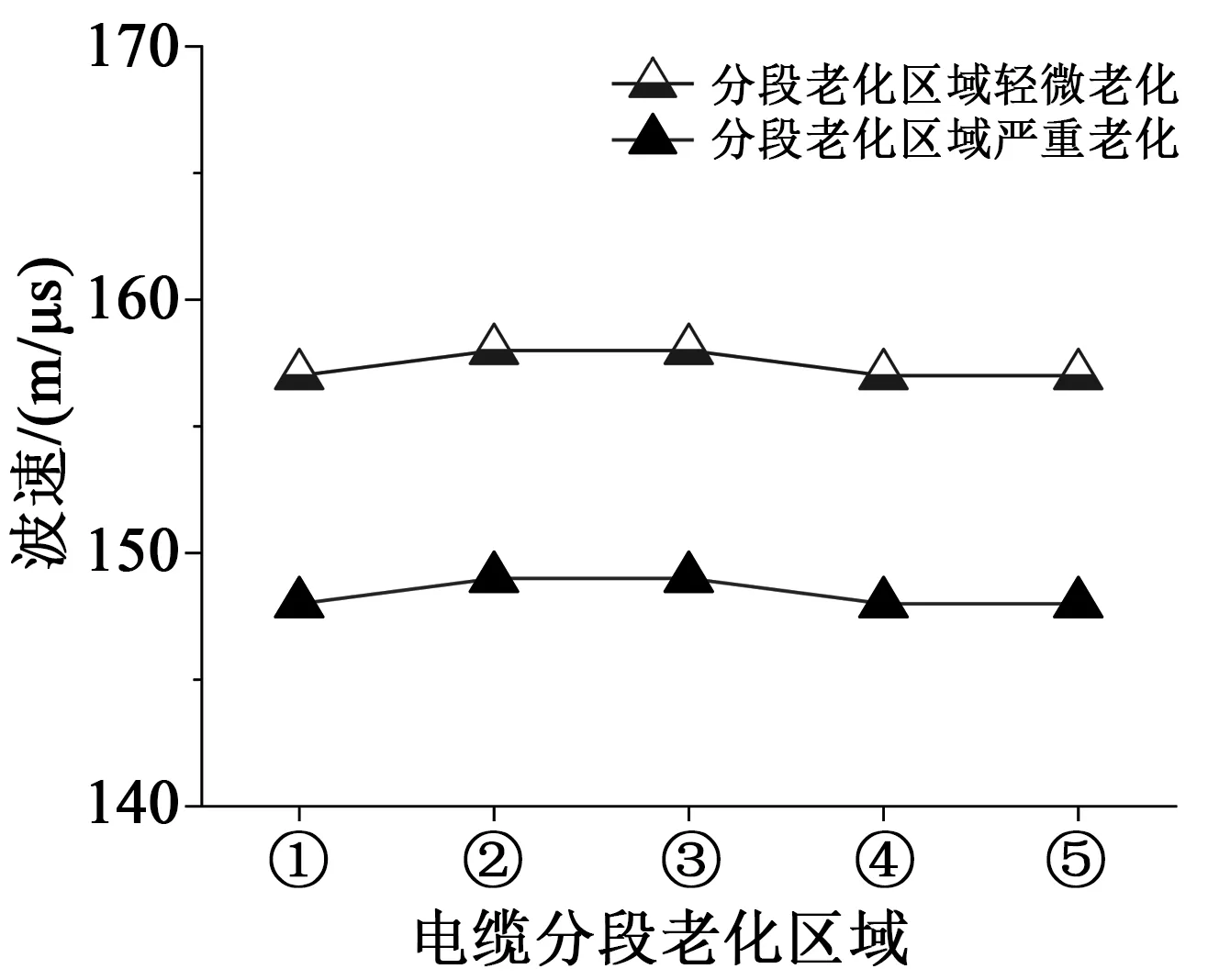
圖8 分段老化電纜平均波速和老化區域位置分布的關系Fig.8 Correlation between average wave velocity and distribution of ageing areas of segmented-ageing cables

基于上述仿真研究可以看出，對于均勻老化電纜而言，電纜老化越嚴重，電纜波速越小，且電纜波速與電纜長度無關；對于分段老化電纜而言，電纜分段老化嚴重程度或分段老化區域長度占比的增加同樣會導致電纜中平均波速的降低，且電纜平均波速與分段老化發生位置基本無關。因此，可以基于電纜中平均波速診斷電纜整體老化狀態。

3 試驗研究

為驗證本研究所提的電力電纜本體整體絕緣老化狀態診斷方法的有效性，在實驗室搭建了如圖9所示的測試平臺。

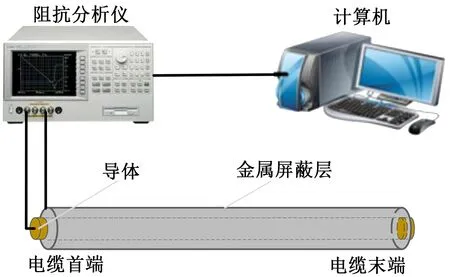
圖9 電纜缺陷定位試驗平臺Fig.9 Test platform for defect location of the cable

首先利用Agilent 4294A型阻抗分析儀測量了長度為99 m的單芯10 kV XLPE電纜在末端開路狀態下的阻抗幅值頻譜，測試頻譜范圍為40 Hz～20 MHz，測量結果如圖10所示。

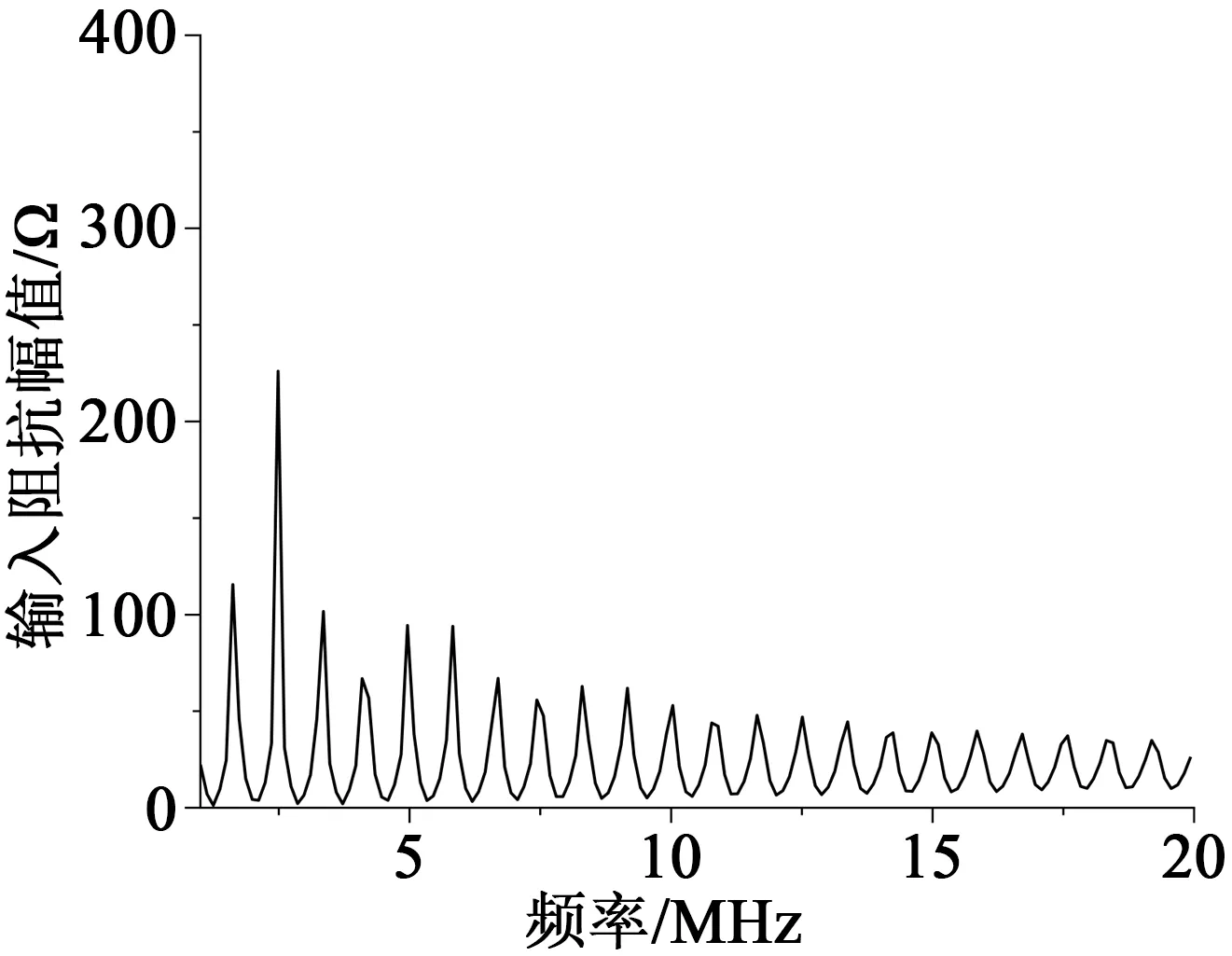
圖10 未老化電纜的首端輸入阻抗幅值頻譜Fig.10 Amplitude spectrum of input impedance at the head end of the unaged cable

隨后，截取長度為3.18 m的電纜，用大電流發生器給電纜導體加熱，模擬電纜實際過載運行導致的絕緣熱老化，其中導體線芯溫度控制在135℃，室溫為25℃，老化時間為64天。老化完成后，利用阻抗分析儀測試了老化后電纜的阻抗幅值頻譜。隨后將此3.18 m老化電纜與同型號4.06 m未老化電纜串聯構成分段老化電纜，同樣對其輸入阻抗幅值頻譜進行測試。兩次阻抗幅值頻譜的測試頻率范圍均為40 Hz～30 MHz，測量結果如圖11所示。

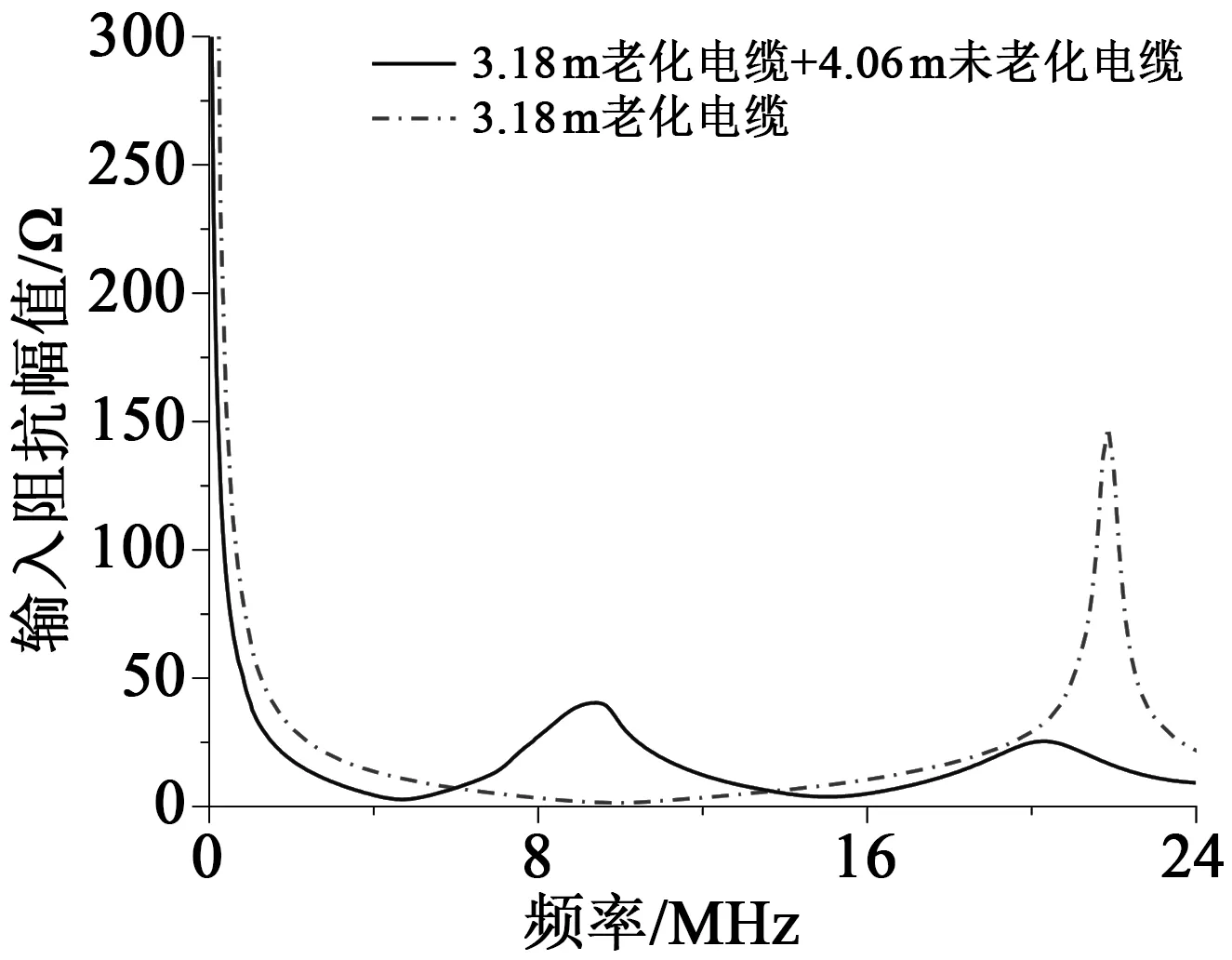
圖11 熱老化后電纜的輸入阻抗幅值頻譜Fig.11 Amplitude spectra of input impedance of the cable after thermal ageing

在此基礎上，利用式（6）計算各電纜中的平均波速，得到未老化電纜、分段老化電纜以及老化電纜中平均波速值分別為166、152、139 m/μs。均勻熱老化后電纜波速相較老化前降低了16.3%，降低幅度較為明顯。與此同時，分段老化電纜中的平均波速高于均勻老化電纜中波速，低于未老化電纜中波速。上述試驗結果表明，無論電纜發生均勻老化還是分段老化，電纜中的平均波速均會有所降低，基于電纜平均波速可有效表征均勻老化電纜和分段老化電纜的整體老化狀態。

此外，王曉威[21]對上述老化前后電纜絕緣部分內、中、外3層絕緣材料的力學性能進行了測試，將本研究電纜中波速測量結果與其測試結果對比如表3所示。從表3可以看出，電纜老化后絕緣部分各層的斷裂伸長率顯著降低，波速在一定程度上可與斷裂伸長率和波速的變化很好地對應。

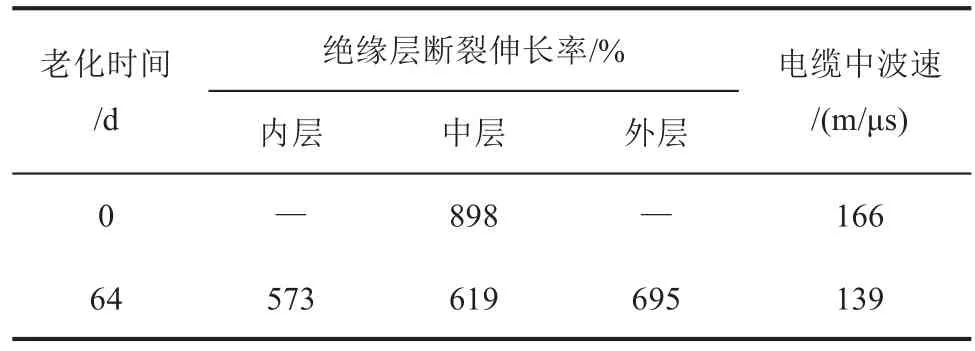
表3 電纜老化前后性能參數對比Tab.3 Comparison of performance parameters of the cable before and after ageing

4 分析與討論

時域反射技術同樣可以用于電纜中波速的測量，但測量過程中會由于時域脈沖傳播過程中的波形畸變而影響波速計算結果的準確性；與此同時，當電纜長度較短時對于測試儀器性能要求較高。而本研究提出的基于輸入阻抗譜的波速計算方法原理主要基于電纜線路阻抗頻譜“諧振”效應，其“諧振頻率”基本不受波形畸變影響，在一定程度上可以提高波速測量準確性[22]。此外，考慮儀器自身采樣率對于輸入阻抗幅值頻譜波形完整性的影響，可利用多個諧振周期頻率間隔值來計算電纜中的波速以降低誤差。

5 結論

（1）電纜老化會引起絕緣結構相對介電常數的增大，導致電纜中高頻電磁波傳播速度的減小。本研究利用電纜輸入阻抗幅值頻譜計算電纜中平均波速，并據此提出基于電纜中平均波速診斷電纜整體絕緣老化狀態的方法。

（2）對于均勻老化電纜而言，電纜老化越嚴重，電纜中波速越小，且波速與電纜長度無關；對于分段老化電纜而言，電纜分段老化嚴重程度或分段老化區域長度占比的增加均會導致電纜中平均波速的減小，且電纜平均波速與分段老化發生位置基本無關。

（3）基于試驗研究發現電纜熱老化后絕緣層的斷裂伸長率和電纜中波速均有所降低，且這兩種性能參數的變化趨勢可以很好地對應，驗證了基于波速診斷電纜絕緣老化狀態的有效性。