水下絞籠式挖溝機機械開挖數值分析
王 亮,李軍營,盧正超,尚智敏,季春光,張其一
1.海洋石油工程股份有限公司,天津 300456
2.天津市精研工程機械傳動有限公司,天津 300409
3.中國海洋大學工程學院,山東青島 266100
海底管道是海洋油氣田開發(fā)中輸送油氣資源的重要設施,為維持其自身安全和在位穩(wěn)定性,免遭拖網漁具等的損害,必須埋設到預定的深度[1]。根據海床的開溝成型方式,常用的挖溝機技術主要有四種類型:機械挖溝法、水力噴沖法、機械和水力結合法、管道自埋法。歐美國家在海床挖溝方面積累了大量的工程經驗,比如SMD公司、IHC公司、Forum Perry公司等[2]。我國在海床挖溝設備的研發(fā)上起步較晚,目前以挖溝犁和噴沖式挖溝機為主,大部分挖溝機自身無動力,需要拖船輔助施工,很難完成深水區(qū)域硬質海床的挖溝任務[3]。隨著我國海洋強國戰(zhàn)略的推進,海底管道挖溝設備將迎來巨大的挑戰(zhàn)。
Bang等人對二維平面定點射流問題進行了研究,結合黏塑性理論得到水流相與泥沙相的通用控制方程[4]。錢忠東等采用了歐拉多相流模型,開展了大量的沖刷研究[5]。孟然利用Flow-3D軟件對噴沖式挖溝機挖溝過程進行數值模擬,得到沖刷時懸沙濃度分布及底沙沖刷情況[6]。顧磊等采用耦合的歐拉-拉格朗日方法 (ALE)計算了射流沖刷砂土和黏土的問題[7]。Huang等采用離散單元法開展了三維流體力學計算,分析了射流規(guī)律對海床沖刷坑的影響[8]。Machin對海底挖溝機的設計現狀進行了總結,指出目前對射流侵蝕深度的預測方法主要是根據土力學中的承載力理論,在土體性質分析中,除剪切強度外,土體的抗拉強度和液塑性質也對其有很大的影響[9]。
本文采用非線性流固耦合理論,利用Abaqus的CEL數值方法,對水下絞籠式挖溝機進行了詳細的計算,其一求解挖溝過程中絞籠對土體的切削作用與破土機理;其二給出簡潔、高效的絞籠切削阻力計算公式;其三給出準確的拖輪橫向拖曳力計算公式。
1 數值模型
1.1 歐拉大變形數值算法
在數值計算過程中,傳統(tǒng)的拉格朗日分析法適用于小變形情況,材料與網格節(jié)點綁定并充滿網格,計算過程中節(jié)點與材料綁定,外部荷載作用下網格單元發(fā)生變形;當荷載突變或量級較大時,單元網格將會發(fā)生畸變,從而導致數值計算無法收斂。
采用歐拉-拉格朗日算法時,計算過程中網格節(jié)點在空間中固定,物質材料能夠在網格內部流動,即使材料發(fā)生過大扭曲,單元網格也不會發(fā)生變形,所以數值計算過程中具有較好的收斂性。非線性有限元軟件Abaqus結合了二者的優(yōu)點,采用了耦合的歐拉-拉格朗日(CEL)方法,可以通過分析歐拉材料的體積分數(EVF)來跟蹤其流經網格的情況,克服了傳統(tǒng)有限元分析方法在處理大變形問題上的困難。兩種計算方法示意圖如圖1所示。
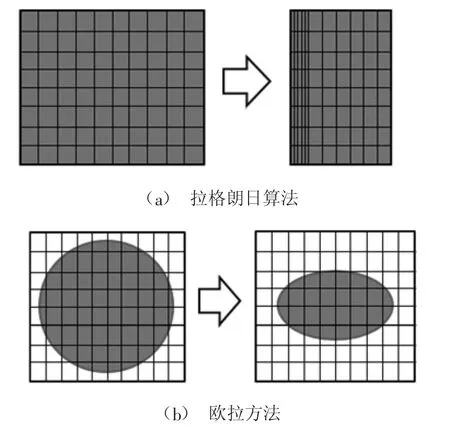
圖1 拉格朗日法和歐拉法的變形分析
數值計算過程中采用能量守恒方程,CEL算法采用空間導數的形式描述,而拉格朗日算法則采用物質導數來描述,空間導數與物質導數間映射關系如下:
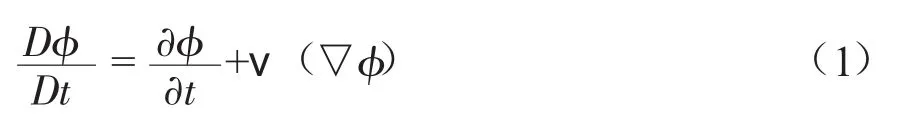
根據式(1)應用于物質導數表示的連續(xù)、動量、能量守恒方程,可以推導出空間導數表示的Euler方程組:
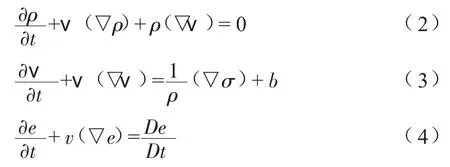
式中:ρ為密度;σ為柯西應力;b為體力;e為單元體積內能。
1.2 模型建立
絞籠式挖溝機有限元網格模型如圖2(a)所示,包括:前置6個機械式絞籠切削裝置、后置大口徑噴沖裝置、尾部抽吸揚泥臂。數值計算過程中,絞籠式挖溝機采用小變形的拉格朗日彈性材料進行模擬。
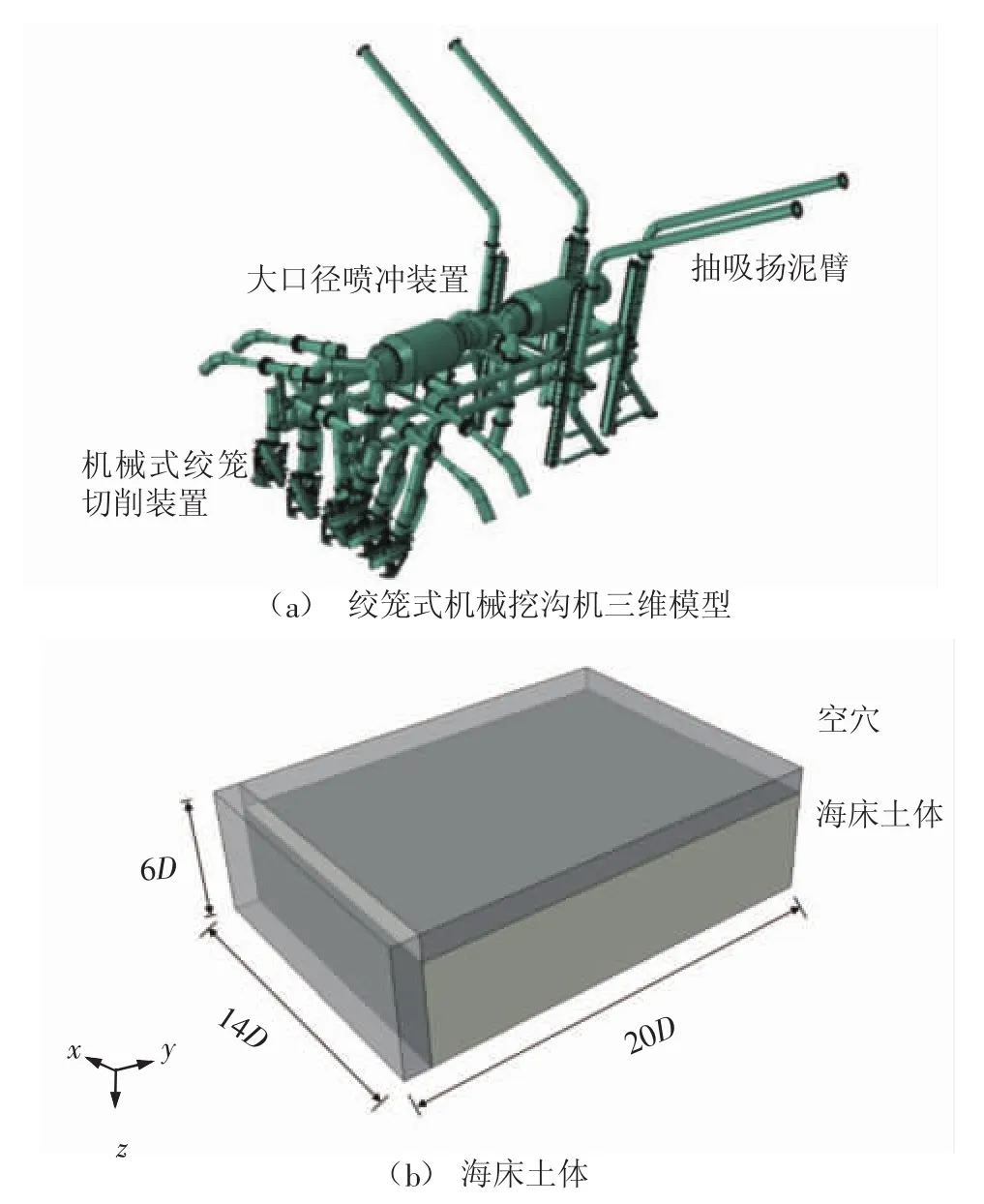
圖2 絞籠式挖溝機有限元模型
海床土體設定為歐拉體,如圖2(b)所示,采用上述CEL算法進行求解,土體本構關系采用Mohr-Coulomb模型,土體參數如表1所示。在挖溝過程中,由于絞籠的旋轉切削作用,絞籠周圍土體會發(fā)生隆起與擴散,故在海床土體頂部設置空隙層,以避免土體的邊界流出;土體模型寬度取為14倍的絞籠直徑D,長度取為20倍的絞籠直徑,高度取為6倍絞籠直徑。數值計算過程中,采用速度邊界條件對海床土體施加速度約束,在絞籠旋轉軸上施加既定的角速度來實現絞籠對土體的切削作用,歐拉材料與拉格朗日體之間的相互作用使用通用接觸對來定義。

表1 海床土體模型參數
1.3 模型驗證
為了確保數值求解結果的準確性,需要對數值模型的網格類型與節(jié)點數量進行對比試算,同時合理調整數值模型的邊界條件。本文計算過程中,通過多次調整單元類型、節(jié)點數量與網格密度,最終選擇了網格單元數目為2 985 618,單元類型為EC3D8R來進行數值仿真計算。試算過程如表2所示。
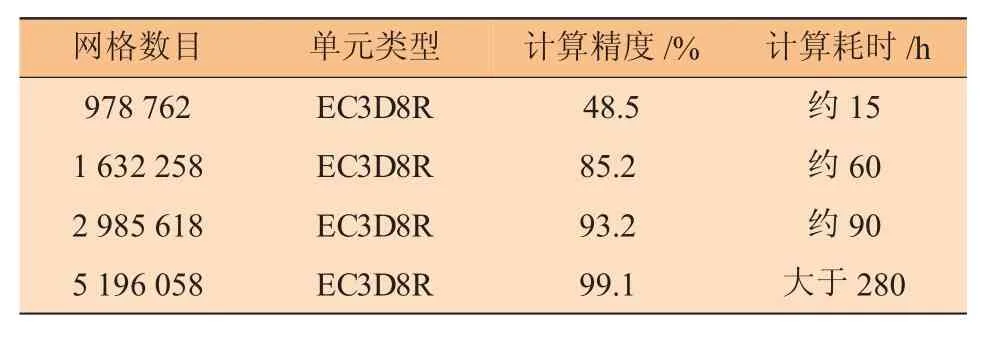
表2 數值網格驗證
2 數值計算
為了較為準確地對絞籠挖溝過程進行模擬,分析土體的變形規(guī)律與絞籠的切削阻力,本文采用了圖3所示的4套絞籠模型進行計算。
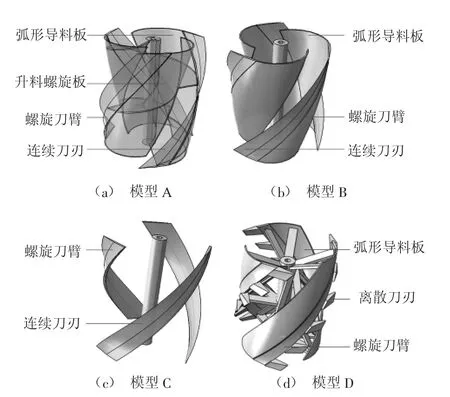
圖3 三維絞籠
圖3所示的4組絞籠中,圖3(a)包含了升料螺旋板、弧形導料板、螺旋刀臂和連續(xù)刀刃;圖3(b)包含了弧形導料板、螺旋刀臂和連續(xù)刀刃;圖3(c)由螺旋刀臂和連續(xù)刀刃構成;圖3(d)為卸除了螺旋升料板優(yōu)化后的絞籠。
2.1 土體變形規(guī)律
在絞籠旋轉切削作用下,絞籠鈄齒前方土體被切削破碎,切削土層塑性應變如圖4所示。
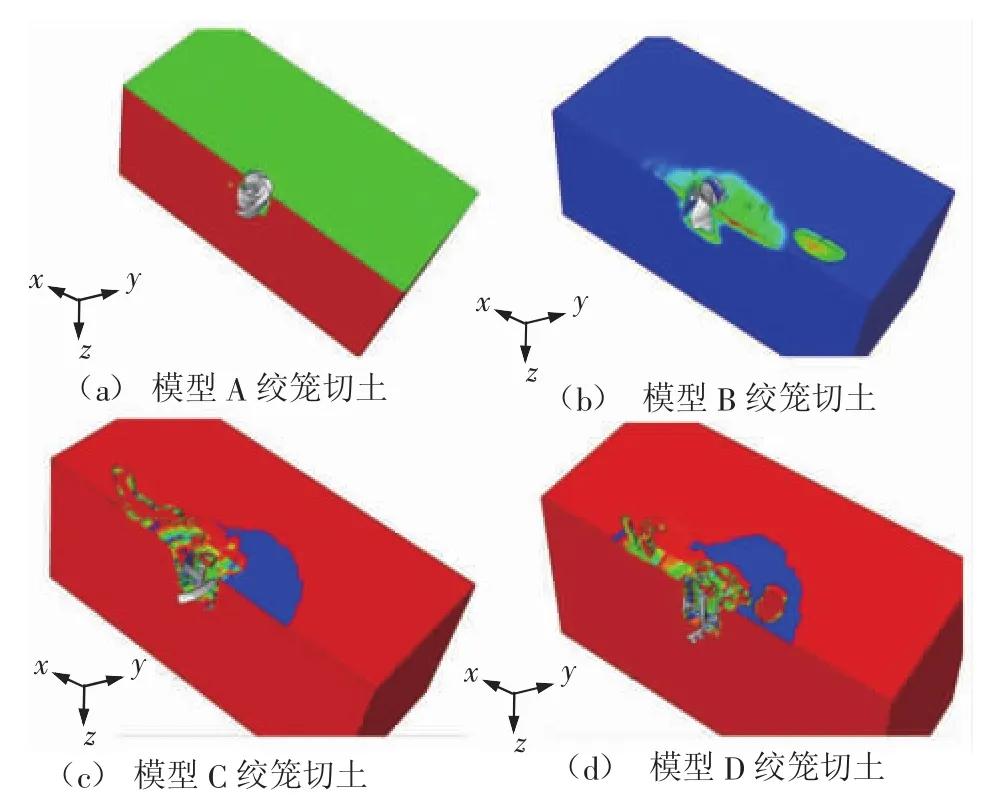
圖4 絞籠切削土層塑性應變
根據圖4(a)計算結果發(fā)現,在絞籠升料板存在較大摩擦系數的情況下,容易出現切削土料堵塞絞籠的情況;大量計算結果表明,當將升料板的摩擦系數降低(極限值為切向摩擦系數設為0),絞籠的水平切削力降低比較明顯。根據圖4(b)計算結果發(fā)現,當拆除升料板后,絞籠切削下來的土體不再受到升料板的摩擦約束,切削土料能夠順利地從絞籠排出,這種情況下的絞籠挖溝過程所需要的水平切削力較小。由圖4(c) 計算結果可見,當同時去除升料板和導料板后,絞籠切削后的土體成條狀,對土體產生的破碎效果較弱,所以絞籠中的導料板需要保留,用于進一步破碎土體。圖4(d)計算結果顯示,將連續(xù)的一字刀刃更換為離散的刀齒后,絞籠挖溝過程中破碎土體的效果更為明顯;相比一字刀刃而言,離散刀齒更適合破碎較為堅硬的海床。當采用模型D絞籠,海床中的挖溝效果如圖5所示,圖5給出了絞籠切削土體的塑性米塞斯(Mises) 應力。
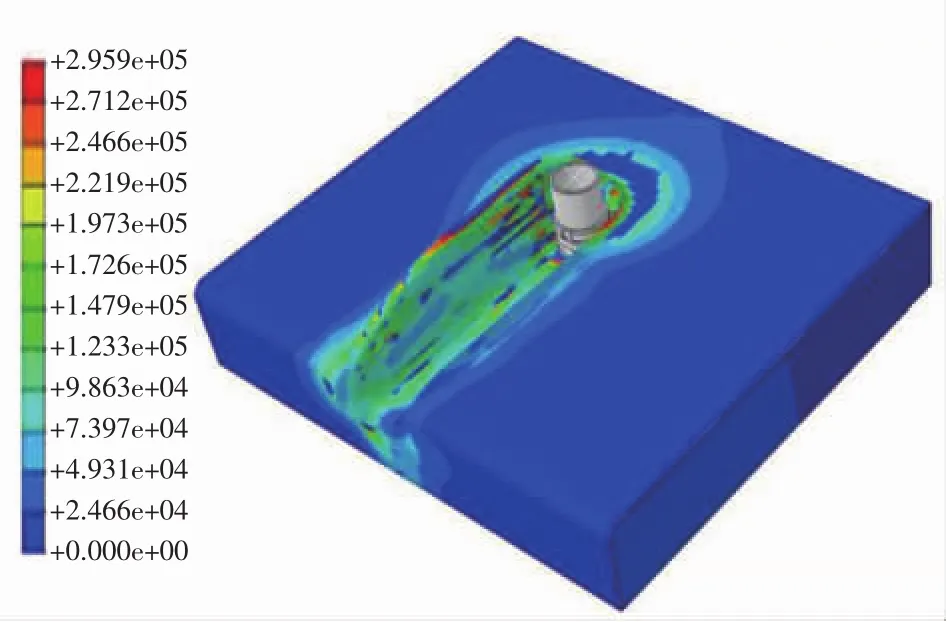
圖5 單絞籠開溝米塞斯應力/Pa
2.2 絞籠切削阻力
為了研究絞籠切削轉速、挖溝機橫移速度(水平行進速度)對切削阻力的影響規(guī)律,針對絞籠挖溝機5種水平行進速度和7種不同的絞籠轉速,開展了35個工況的數值求解,數值求解結果如圖6所示。為了更為方便地計算絞籠的水平切削力,對計算結果進行了歸一化處理,即將水平切削力除以海床土體強度抗剪Su和絞籠橫截面面積A(水平切削力單位為N、橫截面面積單位為m2、海床土體抗剪強度單位為Pa),所以圖6縱坐標表示無量綱的數值。
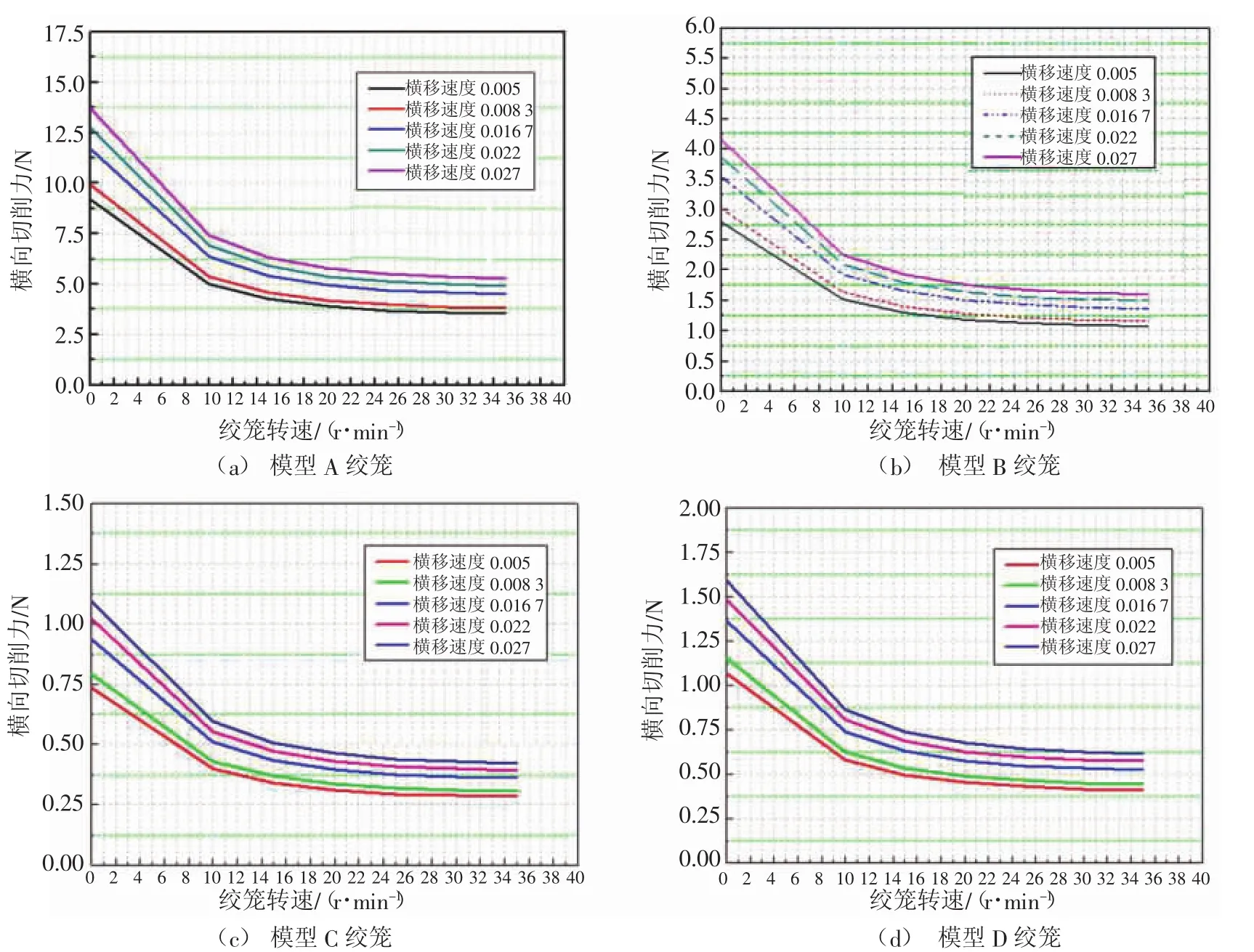
圖6 絞籠切削阻力計算曲線
大量數值計算結果表明,絞籠的旋轉角速度直接影響著絞籠切土過程中的切削荷載,也影響著拖船對挖溝機的水平拖曳力,本文給出絞籠切削荷載經驗計算公式:
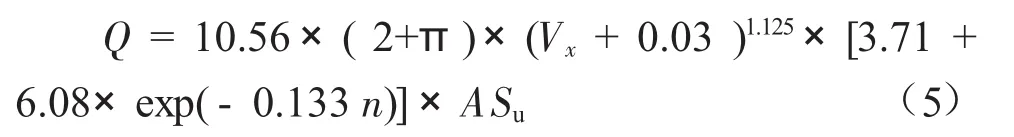
式中:Q為絞籠切削阻力,N;Vx為絞籠挖溝機橫移速度(水平行進速度),m/s;n為絞籠旋轉速度,r/min;A為絞籠橫截面積,m2;Su為土體抗剪強度,Pa。
將式(5)給出的計算值與本文數值計算結果進行對比,對比結果如圖7所示,對比結果顯示本文給出的經驗公式能夠較為準確地求解絞籠式挖溝機的切削荷載。
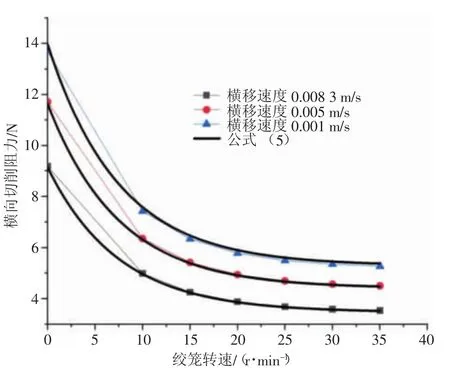
圖7 經驗公式與數值計算結果對比
3 結論
本文基于歐拉-拉格朗日大變形算法,對絞籠式機械挖溝機在海床的作業(yè)過程進行了數值求解,分析了絞籠開溝過程中鈄齒前端土體的變形規(guī)律,同時求解了土體對絞籠的切削阻力,得出的主要結論如下:
(1)絞籠式挖溝機作業(yè)過程中,絞籠轉速越快,刃板上的鈄齒切削土層厚度越小,所產生的切削阻力越小,同時絞籠的水平拖曳力也越小。
(2)本文給出的絞籠切削阻力經驗計算公式,能夠快速、準確地預估絞籠切削阻力,能夠為工程實際提供參考。

