腕臂應力分布與接觸懸掛模態特性研究

馬啟明，吳積欽，謝東旭

0 引言

接觸網是經由集電器向電力牽引單元提供電能的導體系統，由接觸懸掛、支持裝置、定位裝置、支柱與基礎等組成[1]。接觸懸掛由接觸線、承力索、吊弦等零部件構成，直接參與弓網受流，弓網間的動態性能直接影響列車的取流質量[2]。腕臂系統是接觸懸掛的承載者，腕臂定位系統是弓網系統的關鍵結構，其可靠性影響列車的安全穩定運行[3]。研究腕臂系統的應力情況及接觸懸掛的模態特性至關重要。

文獻[4]對惡劣作業環境下接觸網腕臂與絕緣 子之間受力情況進行了分析，但未對應力情況進行分析。文獻[5]對接觸網腕臂結構系統進行了系統的靜力學、動力學仿真，但也未對腕臂系統的應力情況進行說明。文獻[6]對13種具有代表性的腕臂結構有限元模型進行了靜力分析、模態分析、諧響應分析和瞬態動力學分析，但均將腕臂系統與接觸網進行分離，未進行系統考慮。文獻[7]將受電弓采用三維柔性體模型等效，將吊弦視為僅承受拉力的非線性彈簧，接觸網采用三維實體單元離散，通過弓網之間的接觸實現弓網系統的耦合，但未搭建腕臂系統模型且未對接觸網模態特性進行進一步研究。本文采用文獻[8]中的建模方法，按照某既有線路參數建立腕臂系統-接觸懸掛模型，對靜力作用下腕臂系統的應力分布情況及接觸懸掛模態特性進行詳細分析。

1 腕臂系統-接觸懸掛模型建立

某既有線路接觸懸掛參數與腕臂系統參數如表1、表2所示，線路實際布置情況如圖1所示。

表1 接觸懸掛參數

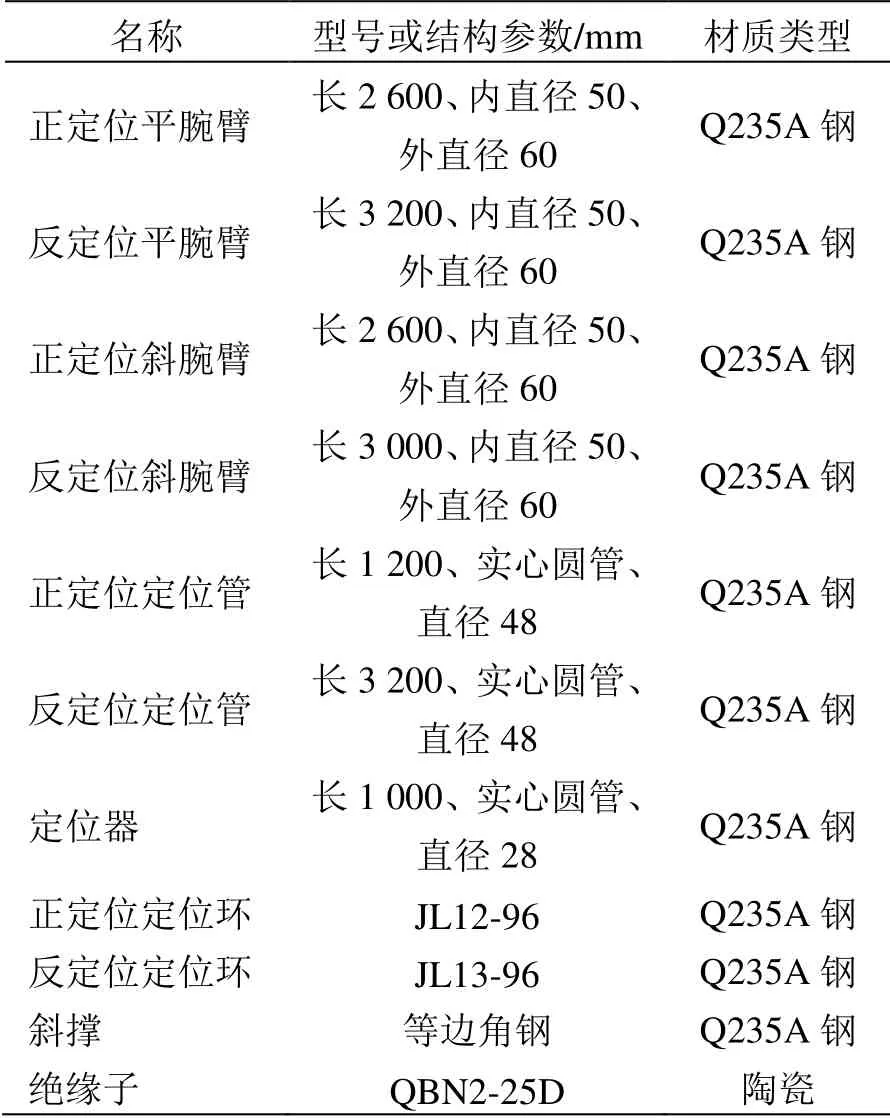
表2 腕臂系統參數

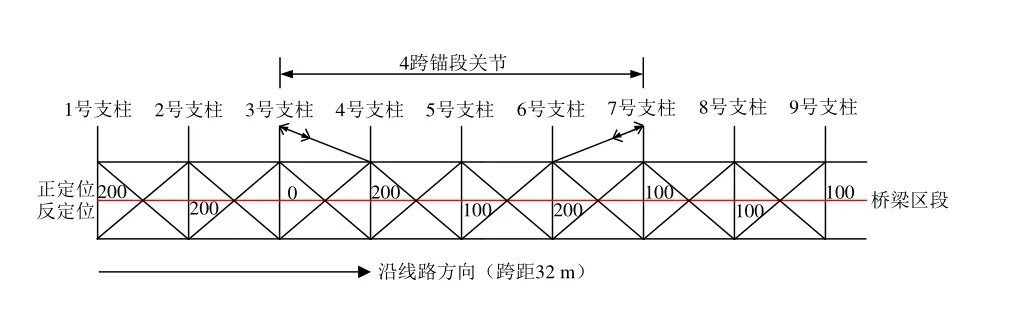
圖1 既有線路現場情況

根據上述參數在ANSYS中建立包含4跨錨段關節在內的共8跨256 m的腕臂系統-接觸懸掛仿真模型，如圖2所示。

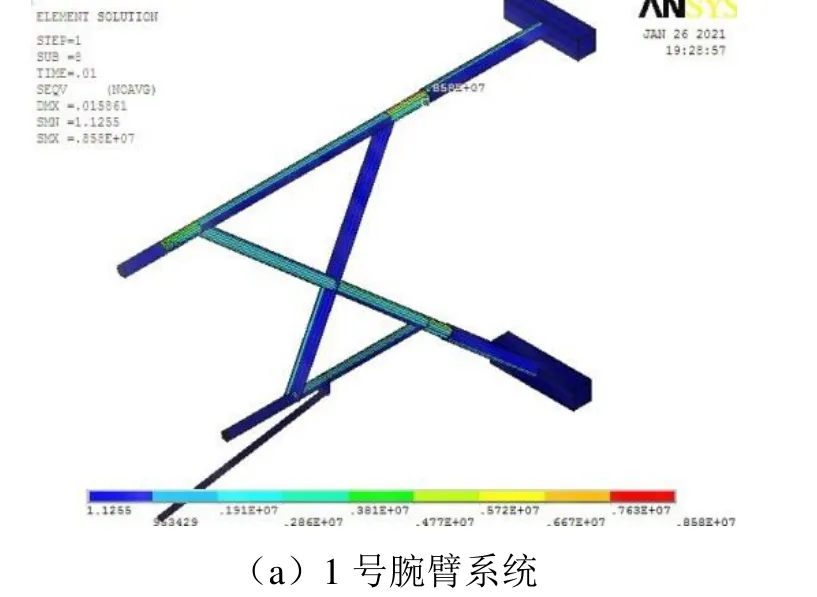
圖2 腕臂系統-接觸懸掛仿真模型

對圖2所示腕臂系統安裝位置設定全約束，將定位環與定位鉤結合位置釋放剛體連接，設置為球鉸并將拉出值所在方向的旋轉進行約束。關于接觸網模型使用的仿真單元，參照文獻[7]中的相關內容進行設定，本文不再贅述。腕臂系統需要考慮其外形對結構性能的影響，本文采用beam188三維空間梁單元進行模擬，beam188單元符合Timoshenko梁[9，10]理論，其動力學方程為

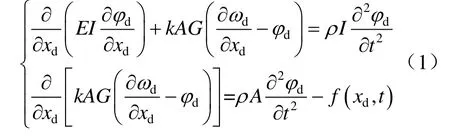
式中：ρ為beam188單元質量密度；I為beam188單元軸向慣性矩；G為beam188單元剪切模量；E為beam188單元彈性模量；A為截面積；φd為beam188單元轉角位移；ωd為beam188單元平動位移；xd為beam188單元軸向位移；f(xd,t)為beam188單元載荷分布；k為Timoshenko剪切系數。

文中所提到的靜力包括接觸線張力、承力索張力及系統所受到的重力，下文將對靜力作用下腕臂系統應力進行詳細分析。

2 靜力作用下腕臂系統的應力情況

提取靜力作用下1～9號腕臂系統的應力情況如圖3所示。 由圖3可知：1號格構鋼支柱承載的腕臂系統最大應力為8.58 MPa，位于平腕臂絕緣子安裝末端；2號格構鋼支柱承載的腕臂系統最大應力為13.8 MPa，位于斜腕臂絕緣子安裝末端；3號格構鋼支柱承載的腕臂系統最大應力為18.3 MPa，位于斜腕臂與平腕臂交叉安裝點處；4號格構鋼支柱承載的腕臂系統最大應力為29.8 MPa，位于非工作支斜腕臂絕緣子安裝末端；5號格構鋼支柱承載的腕臂系統最大應力為10.5 MPa，位于非工作支斜腕臂與平腕臂交叉安裝點處；6號格構鋼支柱承載的腕臂系統最大應力為43 MPa，位于非工作支斜腕臂絕緣子安裝末端；7號格構鋼支柱承載的腕臂系統最大應力為13.8 MPa，位于斜腕臂與平腕臂交叉安裝點處；8號格構鋼支柱承載的腕臂系統最大應力為11.1 MPa，位于斜腕臂絕緣子安裝末端；9號格構鋼支柱承載的腕臂系統最大應力為7.01 MPa，位于平腕臂絕緣子安裝末端。可以看出，腕臂系統的最大應力常位于斜腕臂、平腕臂絕緣子安裝末端或斜腕臂與平腕臂交叉安裝點處，最大應力為43 MPa，可見不同零件的連接位置可能會產生應力集中，若進行動態分析，需對上述位置的應力情況進行重點分析。

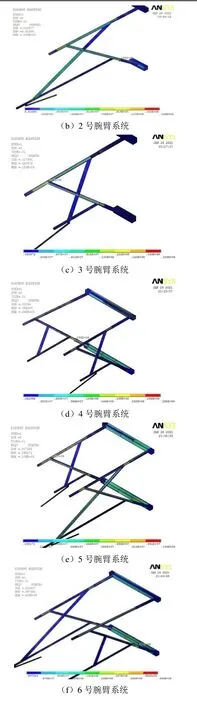
圖3 靜力作用下腕臂系統應力情況

綜合1～9號腕臂系統的等效應力來看，整體處于低應力狀態，均為彈性形變，未發生塑性形變。但絕緣子由陶瓷制成，屬于脆性材料，且應力最大位置多出現于此，在長期運行過程中承受交變應力可能會引起疲勞。斜腕臂與平腕臂交叉安裝點處的應力也相對突出，在安裝時也需保證二者的緊固連接，降低施工誤差。

3 接觸懸掛模態分析

由文獻[1]可知，接觸網是一個具有多自由度的振動系統，該系統存在大量的固有振動頻率。對于由相等跨距組成的鏈形懸掛，存在著對稱和反對稱兩種振動方式。反對稱振動方式下，基波波長等于跨距的2倍，如果將振動波理解為靜止波，其固有頻率為

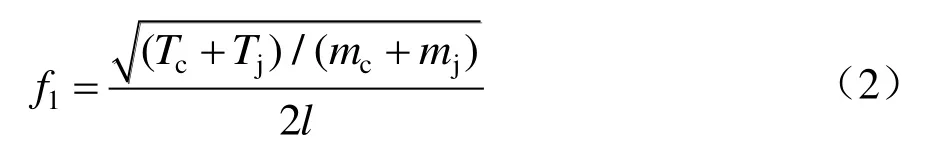
對稱振動方式下，還應考慮第一吊弦所在段，其固有頻率為

式中：Tc為承力索張力；Tj為接觸線張力；mc為承力索質量密度；mj為接觸線質量密度；l為跨距；l1為距定位點最近的兩吊弦的間距。

根據上述計算式可得接觸懸掛的固有頻率：f1= 1.64 Hz、f2= 1.42 Hz。現提取靜力下接觸懸掛的10階模態振型頻率，如表3所示。

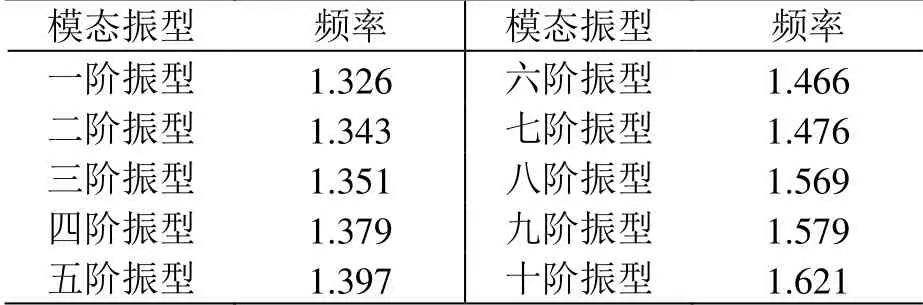
表3 接觸懸掛10階模態振型頻率 Hz

將表3中的10階模態振型頻率對照f1、f2可知計算基本無誤，繪制接觸懸掛10階模態振型如圖4所示。

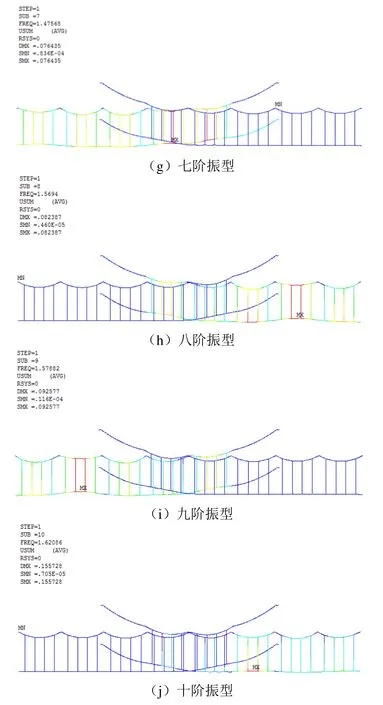
圖4 接觸懸掛10階模態振型

由圖4可知：一階振型對應的頻率為1.329 Hz，第一錨段接觸線沿X正方向移動40.23 mm，且在Y正方向均有所抬升，抬升量最大值為64.03 mm，該位置位于錨段關節處；二階振型對應的頻率為1.343 Hz，第二錨段接觸線在Y正方向均有所抬升，抬升量最大值為79.52 mm，位于第二錨段最后一跨接觸線跨中位置；三階振型對應的頻率為1.351 Hz，第一錨段接觸線在Y正方向均有所抬升，抬升量最大值為67.39 mm，位于第一錨段第一跨接觸線跨中位置；四階振型對應的頻率為1.379 Hz，第二錨段接觸線在Y正方向均有所抬升，較二階振型相比抬升更加明顯，最大值為81.35 mm，位于第二錨段最后一跨接觸線跨中位置；五階振型對應的頻率為1.397 Hz，第一錨段接觸線沿X正方向移動24.23 mm，且在Y正方向均有所抬升，抬升量最大值為91.98 mm，位于第一錨段第一跨接觸線跨中位置；六階振型對應的頻率為1.466 Hz，第二錨段接觸線在Y方向發生正弦式形變；七階振型對應的頻率為1.476 Hz，第一錨段接觸線在Y方向發生正弦式形變，最大值為70.57 mm，位于錨段關節處；八階振型對應的頻率為1.569 Hz，第二錨段接觸線在Y方向發生正弦式形變，且6號格構鋼支柱與7號格構鋼支柱間的接觸線跨中位置沿Z正方向偏移56 mm；九階振型對應的頻率為1.579 Hz，第一錨段接觸線在Y方向發生正弦式形變，最大值為70.57 mm，位于2號格構鋼支柱與3號格構鋼支柱間的接觸線跨中位置；十階振型對應的頻率為1.621 Hz，6號格構鋼支柱與7號格構鋼支柱間的接觸線跨中位置沿Z正方向偏移154.2 mm，嚴重影響拉出值的大小。

由以上分析可知，接觸懸掛的固有頻率主要集中在低頻段內，當外部輸入激勵的頻率與接觸懸掛的固有頻率接近時，接觸懸掛振動程度增強，此時弓網系統動態作用穩定性會降低，易發生弓網接觸力波動加劇，甚至出現弓網離線造成拉弧燃弧，影響接觸網設備壽命。

4 結論

接觸網的腕臂系統承載著接觸懸掛與受電弓進行動態取流，腕臂系統的應力突出位置應引起關注，在日常運維中定期檢查維護，一旦產生疲勞，易造成接觸網坍塌引發重大事故；接觸懸掛需要與受電弓直接作用，會導致兩個相互獨立的振動子系統間產生動態作用，若要避免接觸懸掛共振，保持弓網動態運行的穩定性，必須對接觸懸掛的模態特性進行分析。

本文結合某既有線路參數建立腕臂系統-接觸懸掛模型，對腕臂系統靜力作用下應力分布情況及接觸懸掛模態特性進行了詳細分析，得到以下結論：

（1）腕臂系統整體處于低應力狀態，未發生塑性形變，應力最大位置多出現于絕緣子安裝末端，長期的運行可能會引起疲勞。斜腕臂與平腕臂交叉安裝點處的應力也相對突出，在安裝時需保證平、斜腕臂的緊固連接，降低施工誤差。

（2）接觸懸掛的固有頻率集中在低頻段內，當外部輸入激勵的頻率或弓網間作用頻率與接觸懸掛的固有頻率接近時，接觸網振動加劇，弓網系統動態作用穩定性降低，易使弓網接觸力波動增強，甚至出現弓網離線，造成拉弧燃弧，影響接觸網設備壽命。