洪水沖刷作用下懸空管道力學(xué)響應(yīng)特性研究*

劉興華

中海油安全技術(shù)服務(wù)有限公司湛江分公司

管道是能源的主要輸送媒介，截至目前，全球油氣管道總里程已超1.96×106km[1]。未來十年內(nèi)，全球石油天然氣資源的管道鋪設(shè)仍將持續(xù)進(jìn)行，而長輸管道的發(fā)展伴隨著諸多安全問題。例如我國西氣東輸管線包含尚在規(guī)劃建設(shè)的線路有六條長輸管線，管道沿線不可避免地經(jīng)過河流湖泊等水文地域[2]，當(dāng)河床發(fā)生劇烈變化或發(fā)生大范圍洪水時(shí)，管道在水流沖刷作用下會發(fā)生彎曲變形，嚴(yán)重的甚至發(fā)生折斷，從而造成經(jīng)濟(jì)損失和環(huán)境破壞。

在眾多的管道工程中，洪水對管道的影響引發(fā)了學(xué)者們廣泛關(guān)注，為管道研究工作做出了貢獻(xiàn)。王曉霖等[3]模擬了洪水管道力學(xué)研究模型，推算出管道的變形方程解析式。白路遙等[4]基于河床沖刷深度計(jì)算的經(jīng)驗(yàn)公式建立了更實(shí)用的河段計(jì)算模型。LI Sijia 等[5]利用非線性有限元方法研究漂浮管道的應(yīng)力應(yīng)變，基于管土耦合力學(xué)模型的基礎(chǔ)，建立含缺陷的管道力學(xué)模型。詹婷雯[6]基于Morison 方程建立了洪水作用下管道的數(shù)值模型，詳細(xì)分析了管道的應(yīng)力分布規(guī)律。劉旭等[7]利用有限元模擬結(jié)果建立洪水災(zāi)害下懸空管道的安全評估速查表，提出洪水災(zāi)害下的計(jì)算流程和安全評估措施。王磊等[8]利用Fluent 軟件計(jì)算了輸氣管道外表面的壓力分布，繼而對整個(gè)管道進(jìn)行受力分析。目前的研究主要集中在管道應(yīng)力分布方面，但管道的設(shè)計(jì)多采用應(yīng)變準(zhǔn)則，故同樣需要從應(yīng)變的角度分析管道的失效。本文采用有限元方法建立洪水作用下的管道模型，并討論了關(guān)鍵參數(shù)對管道應(yīng)力、應(yīng)變的影響，研究結(jié)果可為管道的設(shè)計(jì)、防護(hù)提供有力的支持。

1 洪水作用下的懸空管道模型

在洪水沖刷作用下，浸泡的土體會逐漸變得松軟而被沖毀，導(dǎo)致埋地管道產(chǎn)生部分裸露，形成懸空管道，而管道端部仍被掩埋在土體中（圖1）。

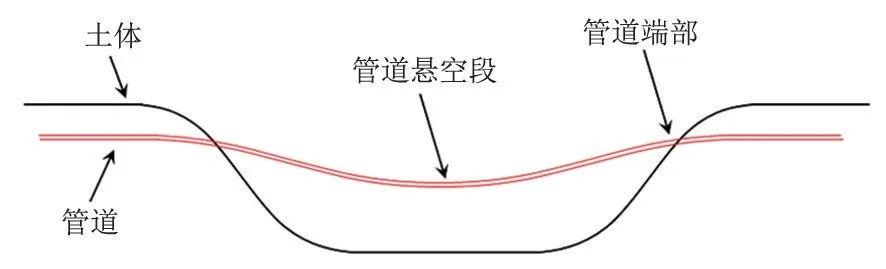
圖1 洪水作用下管道示意圖Fig.1 Schematic diagram of pipeline under flood action

懸空段的管道受力包括管道自身重力、內(nèi)部壓力、管道兩端的管土接觸力。此外，洪水的波浪載荷同樣會作用在裸露的管道外表面，該波浪載荷從方向上可以分為沿管軸方向的動水作用力、垂直沖刷管道的動水作用力及浮力[9]。

懸空段管道截面受力如圖2 所示。依據(jù)Morison方程，在洪水作用下，管道單位長度的動水作用力可具體描述為水流橫向拖曳力FD、豎向升力FL、慣性力FI[10]。

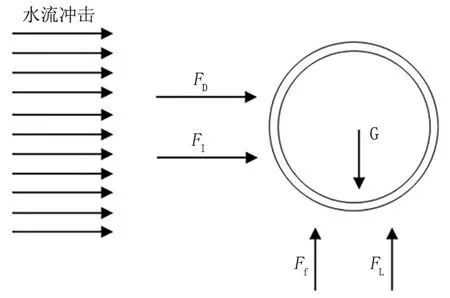
圖2 管道截面所受洪水作用力Fig.2 Flood forces on the pipeline section

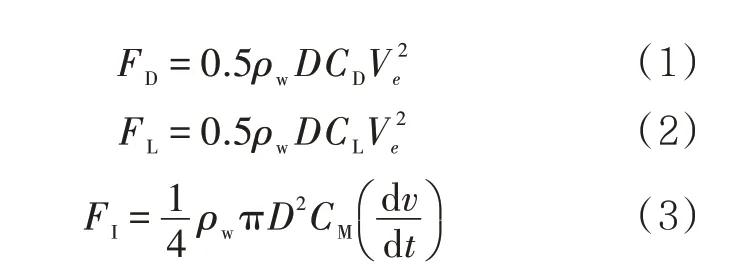
式中：D為管道外徑，m；CD、CL、CM為動水系數(shù)；ρw為洪水密度，kg/m3；Ve為平均水流速，m/s；為水平粒子加速度，m/s2。

單位長度管道重力qw的大小主要取決于管材和管內(nèi)介質(zhì)，即

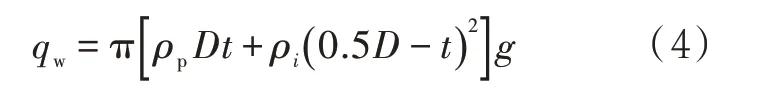
式中：ρp為管材密度，kg/m3；t為管道壁厚，m；ρi為管道內(nèi)介質(zhì)密度，kg/m3；g為重力加速度，m/s2。

由阿基米德定理可得，洪水對單位長度管道的浮力Ff為

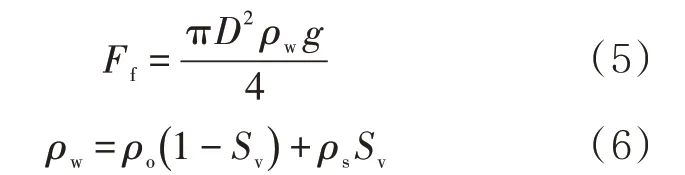
式中：ρo為單位體積洪水和砂的總密度，kg/m3；ρs為單位體積洪水中砂的密度，kg/m3；Sv為體積比砂含量。

其中動水系數(shù)與雷諾數(shù)的關(guān)系如表1[11]所示。

表1 動水系數(shù)與雷諾數(shù)關(guān)系Tab.1 Relationship between hydrodynamic coefficient and Reynolds number

2 數(shù)值模型建立

洪水作用在懸空管道的過程中，管道自身重力影響使得其在豎向方向受力變形。洪水載荷作用后，管道外表面會額外受到水平方向和豎向方向的洪水載荷[12]。除此之外，管道內(nèi)部介質(zhì)同樣會影響管道變形，且管土相互作用對管道端部（管土接觸面）的影響較為明顯。管道是一種薄壁結(jié)構(gòu)，當(dāng)管道截面產(chǎn)生大變形時(shí)會存在殘余應(yīng)力或應(yīng)力集中，如果采用傳統(tǒng)的解析方法很難準(zhǔn)確表達(dá)管道的截面變形，因此采用數(shù)值模擬方法更適合反映洪水作用下的管道力學(xué)響應(yīng)[13]。

建立圖3 所示有限元模型，根據(jù)模型載荷和幾何結(jié)構(gòu)的對稱性，整個(gè)模型采用1/2 模型。假設(shè)土體形狀為立方形，尺寸為12 m×6 m×6 m。油氣管道為X65 鋼級管道[14]，外徑為660 mm、壁厚8 mm，屈服強(qiáng)度為448.5 MPa，管道密度r=7 800 kg/m3，泊松比0.3，彈性模量E=210 GPa。管道端部圍土采用粉質(zhì)黏土，本構(gòu)關(guān)系為理想彈塑性Mohr-Coulomb 模型。假設(shè)土體具有各向同性。土體的密度值為2 000 kg/m3，彈性模量為12 MPa，泊松比取0.25，黏聚力為50 kPa，膨脹角為22°，內(nèi)摩擦角為25°[15]。管道外表面與土體采用允許分離的管土接觸算法，取管土之間的摩擦系數(shù)為0.3[16]。選取洪水速度3 m/s，洪水密度1 120 kg/m3[13]，根據(jù)Morison理論計(jì)算得出水平升力載荷、豎向載升力荷和浮力載荷[17]。

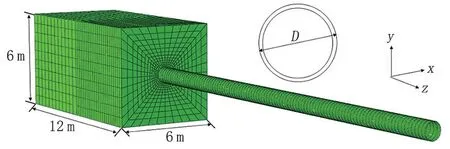
圖3 洪水作用下管道有限元模型Fig.3 Finite element model of pipeline under flood action

管道網(wǎng)格的劃分類型為四節(jié)點(diǎn)殼單元S4R，以C3D8R 八節(jié)點(diǎn)減縮積分單元作為土體網(wǎng)格的劃分類型，然后著重細(xì)化管道附近土體網(wǎng)格[18]。

對整個(gè)模型做以下假設(shè)：延x軸方向?yàn)樗椒较颍貁軸方向?yàn)楣艿垒S向，沿y軸方向?yàn)樨Q向。對整個(gè)模型首先施加初始重力載荷（y軸負(fù)方向），而后施加管道內(nèi)部載荷（作用管道內(nèi)表面），最后施加洪水載荷（x正方向，y正方向）。土體y-z平面和x-y平面分別采用法向（x方向和z方向）約束，x-z底面采用固定約束，土體頂面為自由面。管道對稱面x-y平面采用對稱約束[19]。

3 計(jì)算結(jié)果分析

3.1 懸空長度影響分析

管道懸空后，在自身重力和洪水載荷共同作用下管道受力較為復(fù)雜。圖4 為洪水作用下不同懸空長度管道應(yīng)力云圖。在重力和洪水載荷作用后，最大位移在懸空管道中部（管道對稱面）。當(dāng)懸空長度為100 m 時(shí)，在管道端部（管道出土處）和管道中部（管道對稱面）均出現(xiàn)較大的應(yīng)力集中，但管道端部的應(yīng)力相對大于管道中部。當(dāng)懸空長度增大時(shí)，管道應(yīng)力也不斷增大，其中，當(dāng)懸空長度小于60 m時(shí)，管道端部的應(yīng)力小于屈服強(qiáng)度（448.5 MPa）。當(dāng)懸空長度大于60 m 時(shí)，管道端部的應(yīng)力值大于屈服極限，因此管道發(fā)生塑性變形，但此時(shí)管道中部應(yīng)力仍小于屈服強(qiáng)度，且有逐漸穩(wěn)定的趨勢。在管道端部，當(dāng)懸空長度增大時(shí)，管道的高應(yīng)力區(qū)面積沿管道軸向增大，在懸空長度大于90 m 時(shí)，其軸向的范圍逐漸趨于穩(wěn)定；此外，高應(yīng)力區(qū)同時(shí)也沿管道周向擴(kuò)展，最終在整個(gè)管道周向外表面都呈現(xiàn)較大的應(yīng)力。在管道端部，雖然管道上表面和下表面均有高應(yīng)力區(qū)，但并不嚴(yán)格位于管道正中間，而是與管道正中平面（y-z平面）存在偏離，并呈中心對稱的形式[20]。

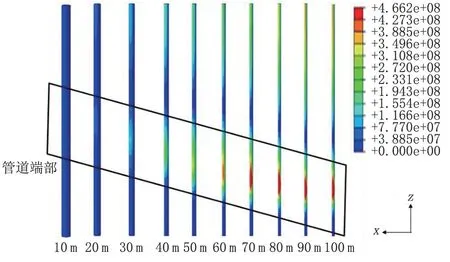
圖4 不同懸空長度下管道應(yīng)力云圖Fig.4 Stress cloud picture of pipeline with different suspended length

圖5 所示為不同懸空長度下管道最大Mises 應(yīng)力。當(dāng)懸空長度小于60 m 時(shí)，最大應(yīng)力的變化率先不斷增大后保持穩(wěn)定。但當(dāng)懸空長度大于60 m時(shí)，管道進(jìn)入屈服階段，最大應(yīng)力開始緩慢增大。

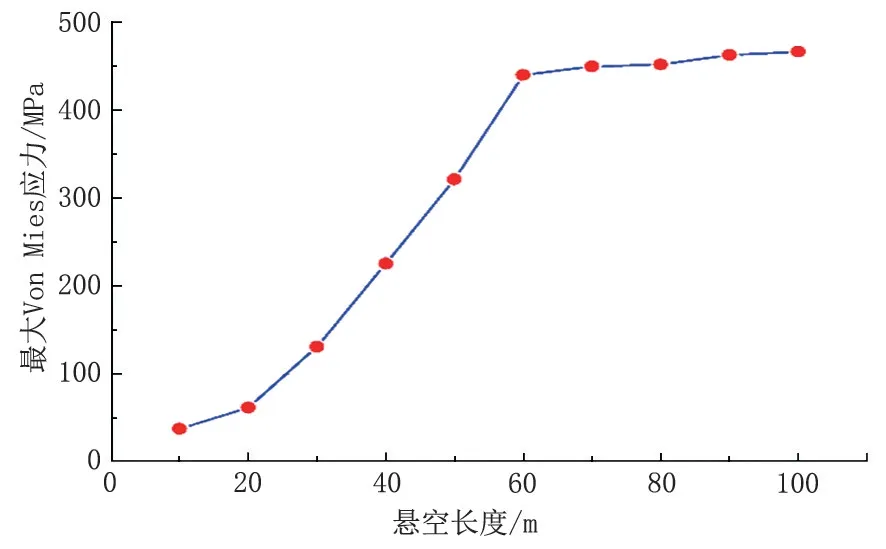
圖5 不同懸空長度下管道最大Von Mises 應(yīng)力Fig.5 Maximum Von Mises stress of pipeline with different suspended length

圖6 所示為不同懸空長度下管道上表面和下表面最大軸向應(yīng)變。管道最大軸向應(yīng)變對應(yīng)管道上下表面最大應(yīng)力，都處于管道端部，管道最大軸向應(yīng)變與正中對稱面存在偏離，但最大應(yīng)變和最小應(yīng)變關(guān)于管道中心近似呈中心對稱。管道上表面受壓，為負(fù)應(yīng)變。管道下表面受拉，為正應(yīng)變。當(dāng)懸空長度小于60 m 時(shí)，管道上下表面最大軸向應(yīng)變變化量較小，變化率近似呈線性。當(dāng)懸空長度大于60 m時(shí)，管道上下表面最大軸向應(yīng)變的變化率明顯增大。根據(jù)CSA 在管道極限狀態(tài)的設(shè)計(jì)準(zhǔn)則，管道應(yīng)變極限值大小應(yīng)為2.5%[21]，故當(dāng)洪水作用下的管道懸空長度大于80 m 時(shí)，管道可能失效。

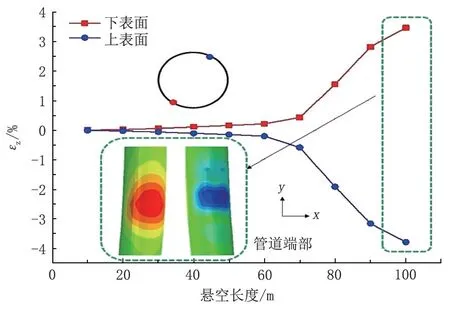
圖6 不同懸空長度下管道最大軸向應(yīng)變Fig.6 Maximum axial strain of pipeline with different suspended length

3.2 洪水流速影響分析

洪水流速會影響管道受到的動水作用力，過大的洪水流速容易造成管道失效。當(dāng)管道懸空長度為50 m，洪水流速范圍為1～5 m/s 時(shí)，管道端部和中部應(yīng)力都隨洪水流速增大而不斷增大，管道端部和中部高應(yīng)力區(qū)域均延管道軸向擴(kuò)展，當(dāng)水流速度大于4 m/s 時(shí)，管道端部開始屈服（圖7）。整體應(yīng)力分布與不同懸空長度時(shí)較相似。由圖8 可知，當(dāng)洪水速度小于4 m/s 時(shí)，最大應(yīng)力隨洪水速度增大明顯，增長率不斷增大。當(dāng)懸空長度大于4 m/s 時(shí)，最大應(yīng)力緩慢增大。

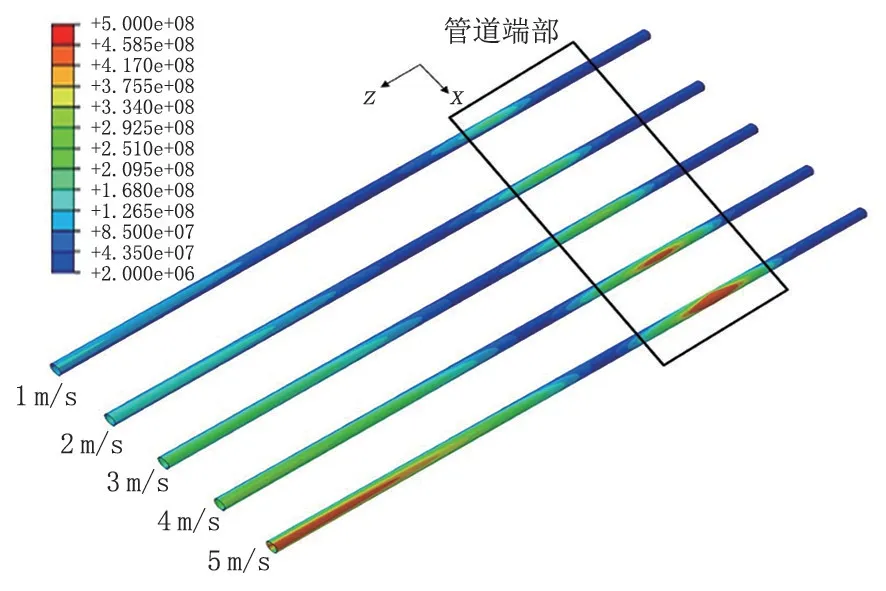
圖7 不同洪水流速下管道應(yīng)力云圖Fig.7 Stress cloud picture of pipeline under different flood velocity

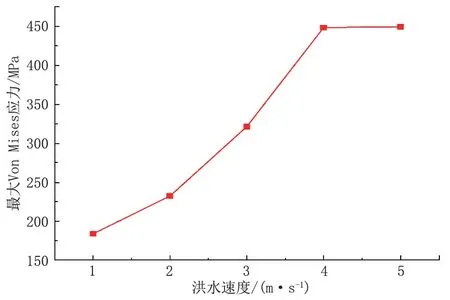
圖8 不同洪水流速下管道最大VonMises 應(yīng)力Fig.8 Maximum Von Mises stress of pipeline under different flood velocity

圖9 所示為不同洪水速度下管道上表面和下表面最大軸向應(yīng)變。管道上、下表面最大應(yīng)變關(guān)于管道中心近似呈中心對稱。當(dāng)洪水速度小于4 m/s時(shí)，隨著水流速度的增大，管道上、下表面最大軸向應(yīng)變不斷增大，且近似呈線性變化。當(dāng)洪水速度大于4 m/s 時(shí)，增長率較大。

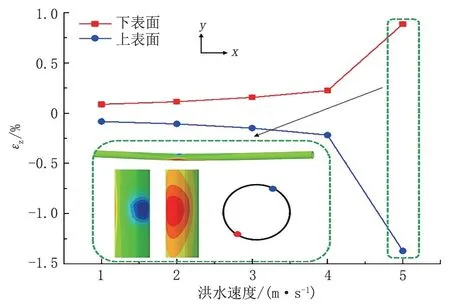
圖9 不同洪水速度下管道最大軸向應(yīng)變Fig.9 Maximum axial strain of pipeline under different flood velocity

3.3 管道壁厚影響分析

管道懸空后在自身重力作用下發(fā)生變形，管道懸空段所受重力與管道壁厚成二次函數(shù)的非線性關(guān)系[12]，因此，壁厚對管道的影響與直徑是存在差異的，當(dāng)懸空長度為50 m 時(shí)，管道整體應(yīng)力隨管道壁厚增大不斷減小，管道端部和中部高應(yīng)力區(qū)變化都比較明顯，因?yàn)楸诤裨龃髸龃蠊艿绖偠龋瑥亩档凸艿雷冃危▓D10）。由圖11 可知，管道最大應(yīng)力隨管道壁厚增大不斷減小，變化率有減小的趨勢，總體變化量比較明顯，約225 MPa，且管道始終沒有達(dá)到屈服強(qiáng)度。

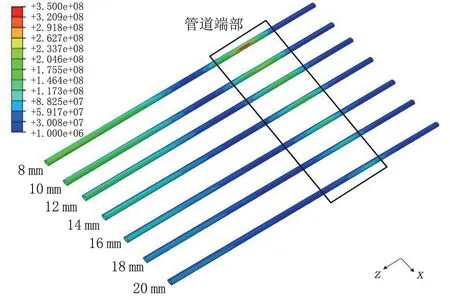
圖10 不同管道壁厚下管道應(yīng)力云圖Fig.10 Stress cloud picture of pipeline with different wall thickness

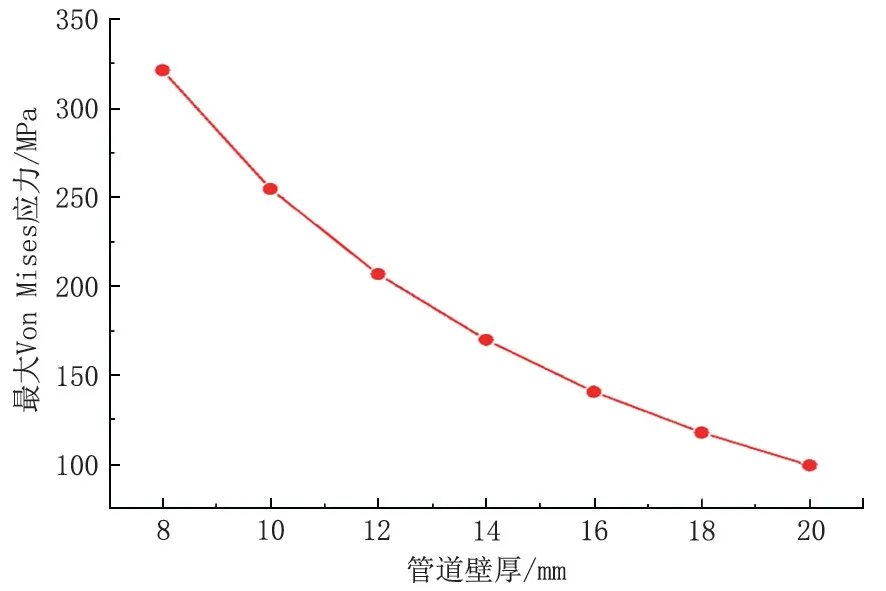
圖11 不同壁厚下管道最大VonMises 應(yīng)力Fig.11 Maximum Von Mises stress of pipeline with different wall thickness

圖12 為不同壁厚影響下管道上表面和下表面最大軸向應(yīng)變。管道上、下表面最大應(yīng)變隨壁厚增大不斷減小，且變化率不斷減小。

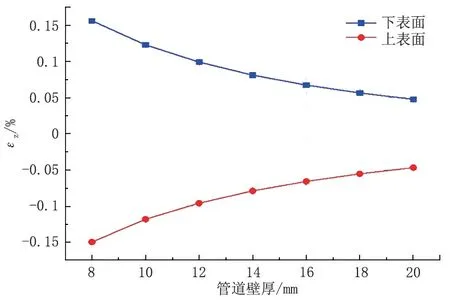
圖12 不同壁厚下管道最大軸向應(yīng)變Fig.12 Maximum axial strain of pipeline with different wall thickness

3.4 管道內(nèi)壓影響分析

當(dāng)管道壁厚為8 mm，懸空長度為50 m 時(shí)，不同壓力管道應(yīng)力如圖13 所示。管道內(nèi)部壓力增大會明顯提高管道應(yīng)力，整體應(yīng)力也會隨內(nèi)壓變化而發(fā)生改變，管道端部和中部的高應(yīng)力區(qū)都不斷增大，并且在高壓下管道容易產(chǎn)生屈服。圖14 為不同內(nèi)壓影響下管道最大Mises應(yīng)力。加大管道的內(nèi)壓導(dǎo)致了管道最大應(yīng)力的增長，變化率不斷減小。當(dāng)內(nèi)壓大于3 MPa 時(shí)，最大應(yīng)力趨于穩(wěn)定，此時(shí)管道已經(jīng)超過屈服強(qiáng)度，最大應(yīng)力增長緩慢，但高應(yīng)力區(qū)會不斷增大。

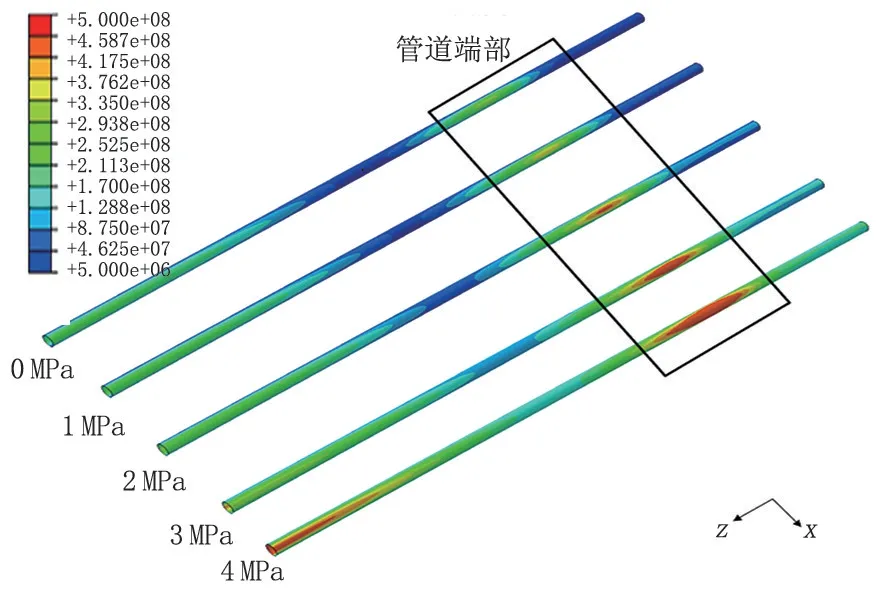
圖13 不同內(nèi)壓下管道應(yīng)力云圖Fig.13 Stress cloud picture of pipeline under different internal pressure

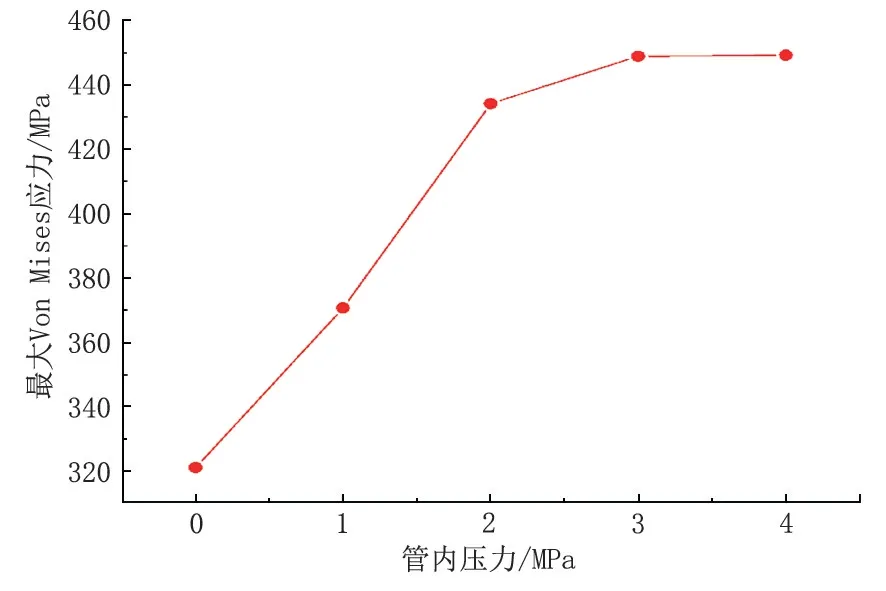
圖14 不同內(nèi)壓下管道最大Von Mises 應(yīng)力Fig.14 Maximum Von Mises stress of pipeline under different internal pressure

圖15 為不同內(nèi)壓影響下管道上表面和下表面最大軸向應(yīng)變。當(dāng)內(nèi)壓小于3 MPa 時(shí)，管道上、下表面最大應(yīng)變隨內(nèi)壓的增大不斷增大，變化率近似呈線性。當(dāng)內(nèi)壓大于3 MPa 時(shí)，最大軸向應(yīng)變增長率增大，軸向應(yīng)變急劇增大。

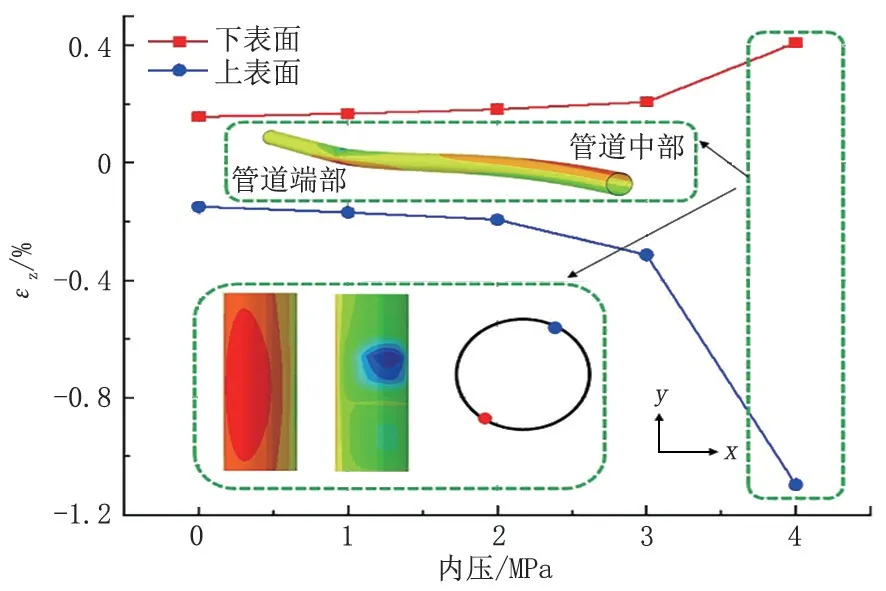
圖15 不同內(nèi)壓下管道最大軸向應(yīng)變Fig.15 Maximum axial strain of pipeline under different internal pressure

4 結(jié)論

（1）采用有限元法建立了洪水載荷下懸空管道數(shù)值模型，研究了懸空管道的變形規(guī)律。發(fā)現(xiàn)隨著管道懸空長度的增大，管道應(yīng)力、應(yīng)變都增大。懸空管道中部和端部均存在高應(yīng)力區(qū)，但最大應(yīng)力在管道端部，當(dāng)懸空長度大于60 m 管端部容易產(chǎn)生屈服。管道上、下表面最大軸向應(yīng)變都位于管道端部，最大應(yīng)變和最小應(yīng)變關(guān)于管道中心近似呈中心對稱。管道上表面為壓應(yīng)變，下表面為拉應(yīng)變。

（2）管道應(yīng)力和軸向應(yīng)變隨洪水速度和管道內(nèi)部壓力增大而增大，當(dāng)懸空長度為50 m，洪水流速大于3 m/s 或管道內(nèi)壓大于3 MPa 時(shí)，管道容易屈服。管道應(yīng)力、應(yīng)變隨管道壁厚增大而減小，且當(dāng)懸空長度為50 m 時(shí)，不同壁厚的管道均未產(chǎn)生屈服。