基于Lasso-Wiener 模型的埋地腐蝕管道可靠性評價

徐恒元 高翔 許小勤 李洪明 姬偉強 劉天峰 喻彥民

1渤海鉆探第四鉆井工程分公司

2青海油田公司

對油氣管道進行風險評價，將事后處理轉為事前預防，是管道完整性管理的重要環節之一。目前，管道風險評價逐步由定性向半定量、定量方向發展[1-3]，TEIXERIA 等[4]基于美國機械工程師協會（ASME）B31G 準則和蒙特卡洛方法計算了腐蝕管道剩余壽命和可靠性；張足斌等[5]通過對5 種剩余強度評價方法進行篩選，采用挪威船級社油氣管道腐蝕評價推薦標準（DNV-RP-F101）和蒙特卡洛方法對在役腐蝕管道可靠性進行評價；韓文海等[6]通過分析海底管道正常運行時可能受到的載荷沖擊，對不同因素下的敏感性進行分析；張新生等[7]通過將灰色模型GM（1，1）和馬爾科夫鏈相結合，根據預測的點蝕深度，實現對未來腐蝕狀態的定量分析。以上研究多參照已有的評價標準，均基于應力-強度干涉原理[8-9]，且樣本數據冗余，對影響因素之間的相關性研究不足。針對腐蝕油氣管道，通過套索回歸（Lasso）算法對影響管道腐蝕的關鍵因素進行提取，將可較好解決外在環境和監測誤差帶來的數據波動的維納（Wiener）模型引入可靠性分析，結合應力加速方程，建立腐蝕速率與應力之間的關系，并進行實例驗證，為埋地管道完整性管理提供理論支持和參考依據。

1 Lasso-Wiener 模型

1.1 腐蝕影響因素分析

待評價管道為一條自中央處理廠至氣體分輸站的輸氣管道，原料氣在中央處理廠進行脫水、脫CO2、脫烴等深度處理，且管道埋地敷設，管輸區域位于平原，地勢平緩，故受內腐蝕和大氣腐蝕的可能性較小，在此重點討論土壤腐蝕對管道可靠性的影響。選取含水量、含鹽量、Cl-含量、含量、含量、土壤pH值、氧化還原電位、自腐蝕電位、土壤電阻率、孔隙度、空氣容量、土壤溫度等12 個因素[10]進行管道可靠性分析評價。

1.2 Lasso 模型

在建立可靠性分析模型時，如將對因變量影響較小的因素選入模型，會降低模型預測精度，延長計算時間，故采用Lasso 算法進行數據降維處理。

Lasso 算法由TISHIRANI 提出，用于高維變量空間獲取稀疏線性模型，不僅可用于線性樣本數據，也可用于非線性樣本數據，在樣本和維度相差不多的情況下可有效避免“維數災難”。原理是基于L1 懲罰函數方法對模型系數進行壓縮，其中系數壓縮為0 的變量視為無關變量，最終只保留顯著變量，同時完成系數估計，達到降維目的。

對任意樣本數據集{X，Y}，其中Xi(i=1，2，…，n)為n組自變量，Yi(i=1，2，…，n)為n組因變量，模型的線性形式為公式（1）所示

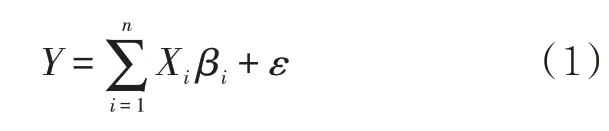
式中：βi為待估計的回歸系數；ε為隨機誤差項，表示不能用自變量X解釋因變量Y的部分。

針對高維、小樣本數據，無法采用最小二乘法對回歸系數βi進行估計，因此將回歸系數的絕對值之和進行懲罰，如公式（2）所示。

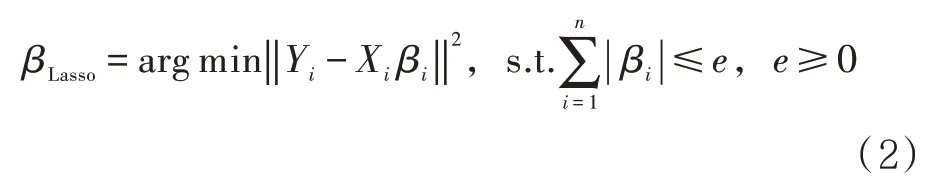
式中：arg min 為公式達到最小值的函數；s.t.為約束條件；e為調整參數。

將公式（2）等價為懲罰函數形式如公式（3）所示。

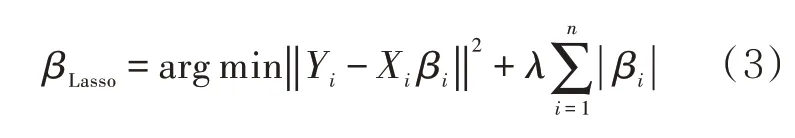
式中：λ為非負正則化參數；為懲罰項。其中λ越大，懲罰項的力度越大，模型中保留變量越多；λ越小，懲罰項的力度越小，模型中保留變量越少。

1.3 Wiener 模型

管道屬線性、長壽命產品，假設退化過程即腐蝕過程是隨時間變化的函數，通過建立合理的性能退化隨機模型對剩余壽命進行準確預測，標準Wiener 退化模型為如公式（4）所示：

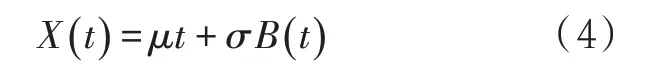
式中：X(t)為管道在t時刻下的退化量；B(t)為時間尺度的單調增函數，用于描述退化的動態特性；μ和σ分別為漂移參數和擴散參數。

考慮到腐蝕過程為非線性，故引入非負時間尺度函數υ對Wiener 退化模型進行改進，將非線性退化轉變為線性退化，如公式（5）、（6）所示。

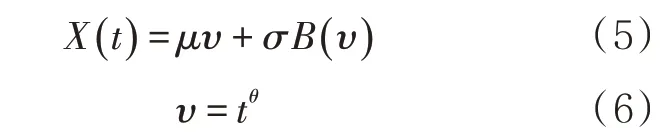
式中：θ為待求參數；B(υ)為表示非負時間尺度的單調增函數；t為時間。

假設l為管道失效閾值，當腐蝕深度達到l時管道失效，剩余壽命T為壁厚減薄至首次達到失效閾值的時間，則

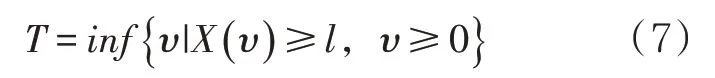
式中：inf為凸優化函數；X(υ)為考慮時間尺度函數下的退化量。

PAN 等[11]和ZHANG 等[12]均證明了逆高斯模型比傳統的腐蝕退化模型更為合理，故剩余壽命T服從逆高斯分布，得到T的分布函數F(T)和概率密度函數f(T)分別如公式（8）、（9）所示。

式中：Φ(·)為標準正態分布函數。

1.4 加速應力方程

經研究表明，壁厚減薄過程具有單調性，且不同應力作用下的加速退化數據具有相同的統計學分布特征，故采用加速應力方程表示剩余壽命和應力之間的關系。應力水平越大，腐蝕速率越大，管道剩余壽命越短，即腐蝕速率與加速應力呈正相關。目前常用的加速方程有廣義艾林模型、冪律模型、阿倫尼斯模型等。假設漂移參數μ與應力有關，而擴散參數σ與應力無關，其中廣義艾林模型屬激活能模型，可用于描述電化學、化學和物質擴散等過程失效機理，則腐蝕速率分布函數可表示為

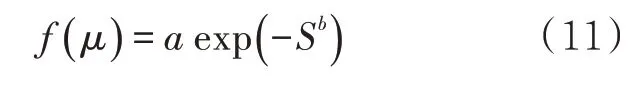
式中：f(μ)為腐蝕速率分布函數；a、b為方程未知參數；S為土壤腐蝕應力。

利用公式（4）～公式（11），將漂移參數μ定為腐蝕速率并作為隨機變量處理，通過加速應力方程建立腐蝕速率與影響因素之間的對應關系，并結合Wiener 退化過程，建立土壤環境下埋地管道的非線性退化評價方法。以管道外徑和壁厚比值不大于100 定義失效閾值，可靠性指標以均勻腐蝕造成的壁厚減薄為主。

2 實例分析

2.1 Lasso 主要因素提取

該地區沿線土壤類型以非黏性內陸鹽漬土為主，土壤理化特性差異較大，腐蝕因素眾多，管道外腐蝕嚴重，管線采用X65 鋼，管徑762 mm，壁厚8.96 mm，最大工作壓力10.5 MPa，最小抗拉強度600 MPa，投產時間為2010 年6 月，設計使用年限30 年。取現場不同區域的40 組土壤腐蝕數據進行分析（表1）。

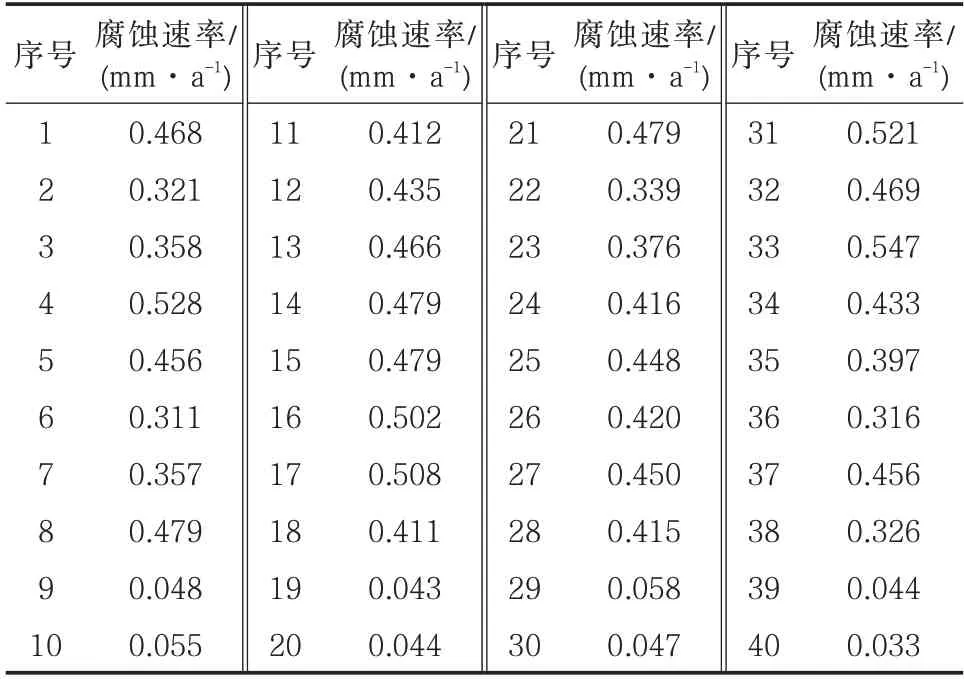
表1 埋片腐蝕數據Tab.1 Embedded plate corrosion data

通過5 折交叉驗證確定非負正則化參數λ=0.441 5，根據λ在不同取值條件下懲罰函數值的變化情況可知（圖1），當λ=0.441 5 時，含鹽量、含量、含量、自腐蝕電位、孔隙度、空氣容量、土壤溫度等因素的懲罰項力度較小，函數值收斂為0。故選擇含水量、Cl-含量、土壤pH 值、氧化還原電位、土壤電阻率等5 個因素作為土壤腐蝕主要因素。

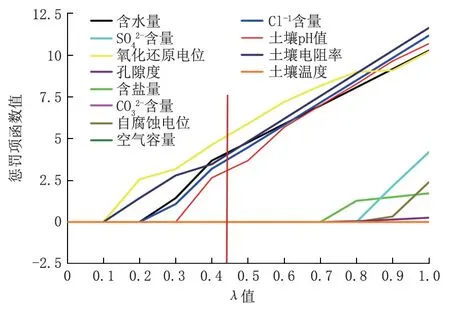
圖1 λ 在不同取值條件下的懲罰函數值Fig.1 Penalty function values of λ under different values

2.2 模型參數估計

將5 個因素作為應力加速方程的顯著性因素，原始數據見表2。將各因素的理化數據取平均值作為代表值，其中含水量為15.43%、Cl-含量為0.152%（質量分數）、土壤pH 值為6.75、氧化還原電位為360.22 mV、土壤電阻率為25.67 Ω·m。對于公式模型中的未知參數σ、θ、a、b，考慮采用極大似然估計法計算復雜性過高，因此采用馬爾科夫鏈-蒙特卡洛方法（MCMC）中的M-H 抽樣算法對未知參數進行估計。由于參數估計過程中存在不確定誤差，假設未知參數的先驗分布均滿足Gamma 分 布，定 義σ～Gamma（0.1，0.01），θ～Gamma（0.1，0.01），a～Gamma（5，10），b～Gamma（5，10）。經過Matalab 編程計算，得到在含水量應力作用下σ、θ、a和b的迭代軌跡（圖2）。迭代次數35 000～40 000 次，當迭代至40 000 次時，兩條初值并不相同的馬爾科夫鏈收斂到一起，迭代軌跡趨于平穩，說明迭代過程收斂。根據退化數據得到參數估計值及95%的置信區間（表3）。其中抽樣誤差較小，且置信區間較窄，說明參數的計算結果準確性較高，用M-H 抽樣算法進行計算是正確的。

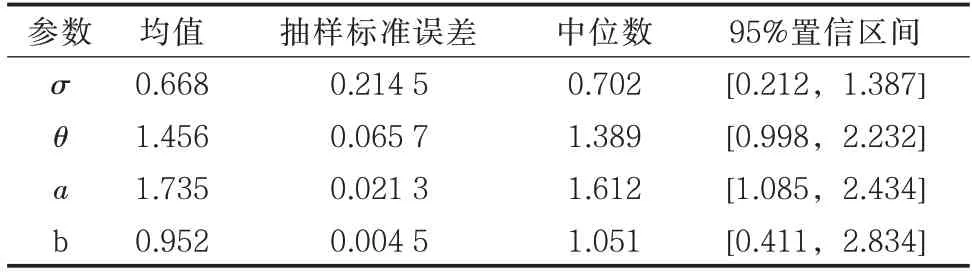
表3 含水量應力作用下的參數估計Tab.3 Parameter estimation under water content stress

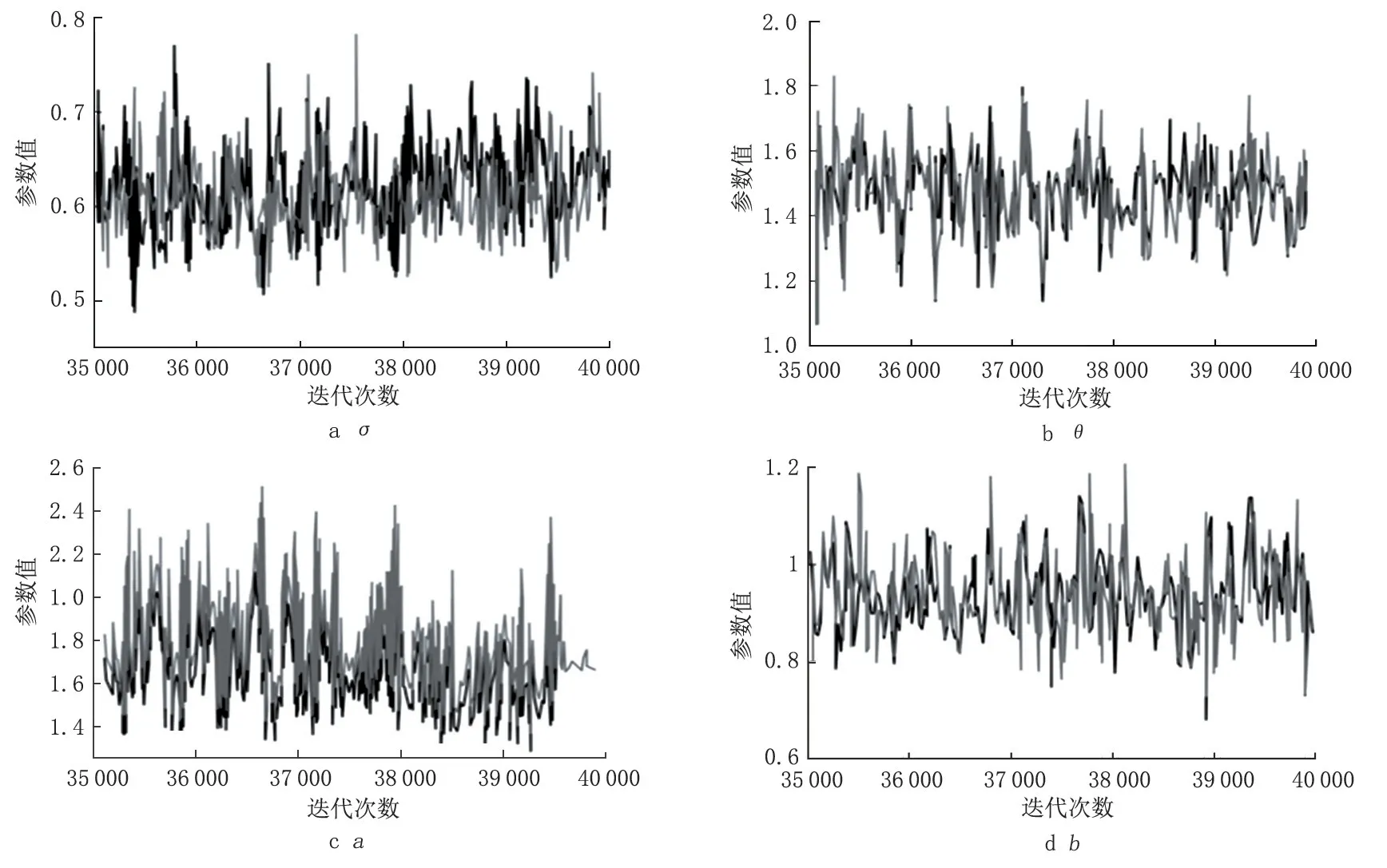
圖2 含水量應力作用下各參數的迭代軌跡Fig.2 Iterative trajectoriy of each parameter under water content stress

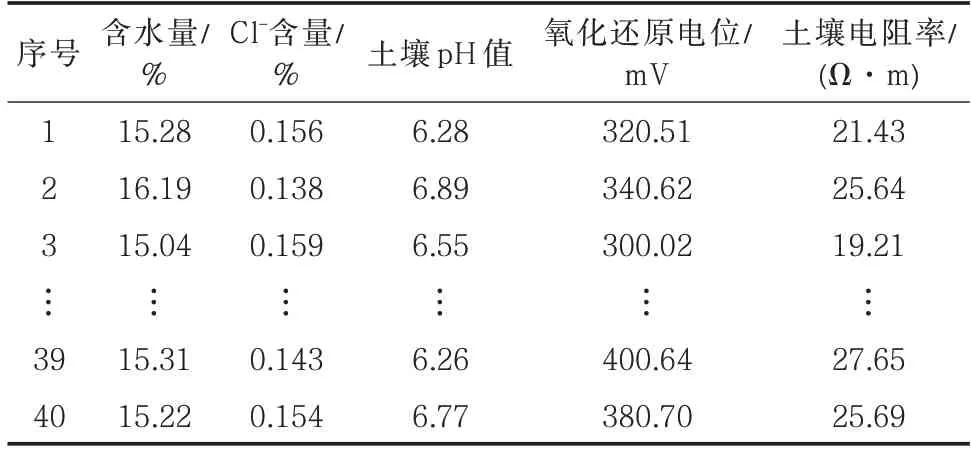
表2 土壤理化特性數據Tab.2 Data of soil physical and chemical properties

同理，對其余應力作用下參數值進行估計，結果如表4 所示。

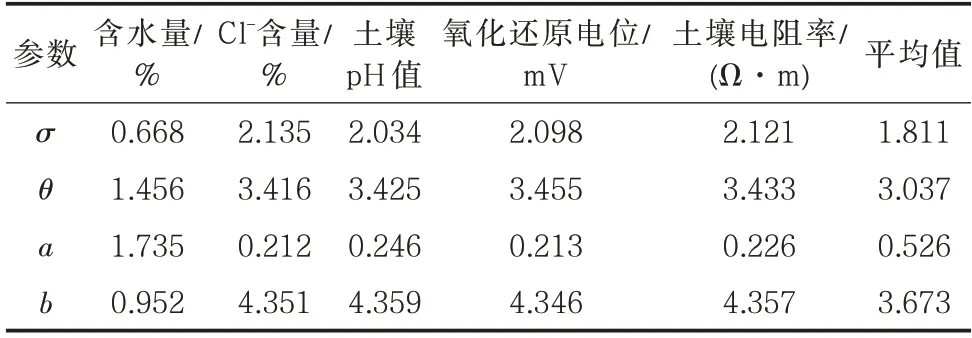
表4 不同應力作用下的參數估計Tab.4 Parameter estimation under different stresses

2.3 埋地管道可靠性分析與評價

將四個參數的平均值作為模型的最終參數，將a=0.526 和b=3.673 代入公式（10），得到5種不同應力作用下的μ值分別0.007、0.257、0.056、0.001、0.007，取平均值為0.064，按照初始腐蝕深度為0，保守估計取失效閾值l為7.2 mm，代入公式（10）中得到

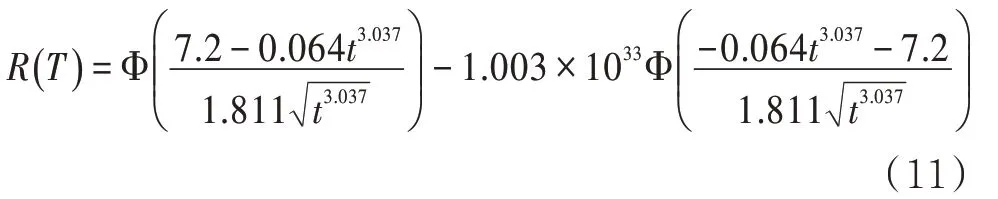
由此，得到該管道的可靠性變化趨勢（圖3）。前10 年管道完全可靠，可靠度為99.15～100%，表示第10 年有99.15%的概率管道可靠，未達到壁厚的失效閾值，未發生因腐蝕造成的泄漏；在11 年時，腐蝕速度加快，可靠度直線下降，在運行到15 年時，可靠度為76.21%；當運行到20 年時，可靠度為38.68%；當運行到設計壽命30 年時，可靠性幾乎為0，此時管道已完全不可用。一般要求可靠度大于90%，可靠度為90%的管道可運行時間為12.5 年，說明在管道服役初期的可靠性良好，但在后期由于腐蝕原因可靠性不斷下降，剩余壽命無法達到當初的設計年限。

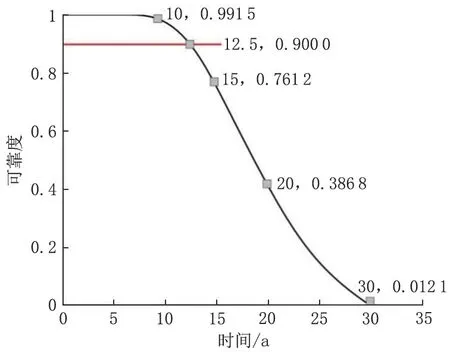
圖3 可靠度計算結果Fig.3 Reliability calculation results

為了驗證計算結果準確性，統計了從投產初期到目前為止的因腐蝕造成的管道穿孔次數（圖4）。前9 年的失效次數較少，在第10 年之后腐蝕速率加快，失效次數大幅增加，管道可靠性降低，與圖3 相比腐蝕加快的時間略有提前，這是由于模型計算只考慮了土壤因素，未考慮其余應力載荷的情況，但總體上符合實際情況，說明將埋地管道的退化預測結果作為指導維護維修策略是合理的。今后應對管道進行實時監控并實施內檢測，以保障管道安全運行。

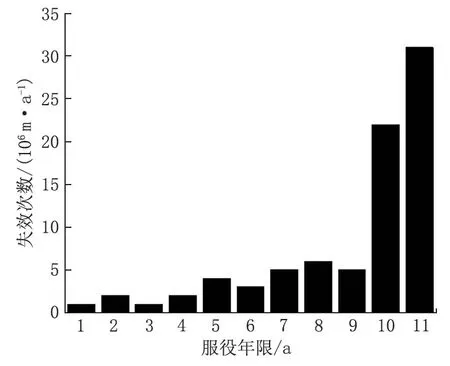
圖4 管道失效次數統計Fig.4 Statistics of pipeline failure times

3 結論

（1）利用Lasso 回歸算法對影響土壤腐蝕的因素進行篩選，選取5 個因素作為土壤腐蝕代表因素，不但可以反應大部分的土壤腐蝕信息，也減少了后續模型的計算量。

（2）引入時間尺度函數對Wiener 模型進行改進，擴寬了Wiener 模型的應用范圍，同時利用加速應力方程描述了腐蝕速率與影響因素之間的關系，強化了模型的因果關系。

（3）通過實例分析，管道可靠性先保持平穩后急劇減小，可靠度為90%的管道可運行時間為12.5年，剩余壽命為14.7 年，與實際穿孔記錄相符。