基于階躍響應的光伏發電最大功率點檢測

林宇杰

（廣東電網有限責任公司佛山供電局）

0 引言

工業革命的發展進一步帶動了能源革命，開啟了大規模的化石燃料利用的序幕。當前社會經濟的快速發展使得以煤、石油等為主的傳統化石燃料的消耗不斷增加，并出現了嚴重的枯竭現象［1］。而太陽能作為一種清潔、無污染、可再生的優質資源，逐漸受到人們的高度關注。當前，太陽能的利用主要可實現光熱的轉換和光電的轉換，其中，光電之間的轉換可以直接應用到光伏效應當中，將太陽輻射直接轉化為電能。為了確保光伏發電系統能夠始終保持穩定的運行狀態，需要對光伏發電的功率進行實時監測，并針對其最大功率點進行獲取，通過對最大功率點的有效控制，確保光伏發電系統的運行性能。早期針對光伏發電最大功率點的檢測能夠針對不同的負載調整相應的光伏陣列，并通過串并聯的組合方式，實現最大功率的輸出［2］。但是在實際應用中，這種檢測方法由于受到周圍環境因素的影響較大，并且實施難度較高，因此存在實時性差的問題，且對于天氣情況存在劇烈變化的地區不宜采用。因此，針對這一問題，為提高檢測方法的適應性，本文結合階躍響應，對光伏發電最大功率點檢測方法進行優化設計研究。

1 基于階躍響應的光伏發電最大功率點檢測

1.1 構建光功率捕獲數學模型

根據太陽能動力學原理，將光功率捕獲的機械能和機械轉矩以如下公式表示，其中機械能的表達式如式（1）所示：

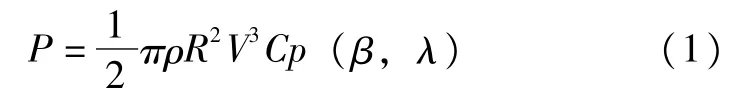
式（1）中，P表示光功率捕獲的機械能；ρ表示空氣密度；R表示太陽電池半導體橫截面半徑；V表示光照強度；Cp（β，λ）表示光能利用系數。

光功率捕獲機械轉矩表達式如式（2）所示：

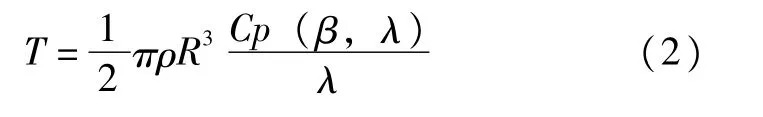
式（2）中，λ表示光伏發電機的運行速率。將式（1）和式（2）作為光功率捕獲的數學模型，為后續模型的線性化處理提供模型基礎。

1.2 基于階躍響應的模型線性化處理

在光伏發電機運行過程中，其補償器的增益數值越大，則其轉矩補償的作用越大，當增益數值為零時，則補償作用同樣為零［3］。在這一特點的基礎上，針對本文上述構建的光功率捕獲數學模型，需要結合階躍響應對其進行線性化處理，得到線性化公式為：

式（3）中，δ表示穩態工作點下的光照強度；Tm表示電池溫度；K表示增益數值。式（3）中，增益數值K的計算公式為：

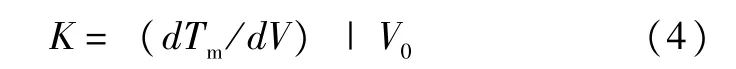
按照式（3）和式（4）得出線性化結果并將其作為最優轉矩計算輸出，將不同增益數值條件下的光伏發電功率的階躍響應曲線進行繪制，并得到如圖1所示的曲線結果。

圖1中KI、KII和KIII分別為三個不同數值的增益，其中KI為1，KII為0.5，KIII為0。從圖1可以看出增益數值越大，光伏發電系統的階躍響應速度越快，達到穩定狀態時所消耗的時間越短，并且沒有出現超調現象。但在達到階躍時負脈沖幅值較大，其主要原因是隨著系統運行響應速度的不斷提高，光伏階躍引起的功率輸出出現了較大的轉變［4］。根據上述得出的結論，在對光伏發電最大功率點進行檢測時，應當結合改進OTC法對最大功率點進行檢測和跟蹤，從而防止在暫態過程中出現超調的現象，確保檢測方法的動態特性。

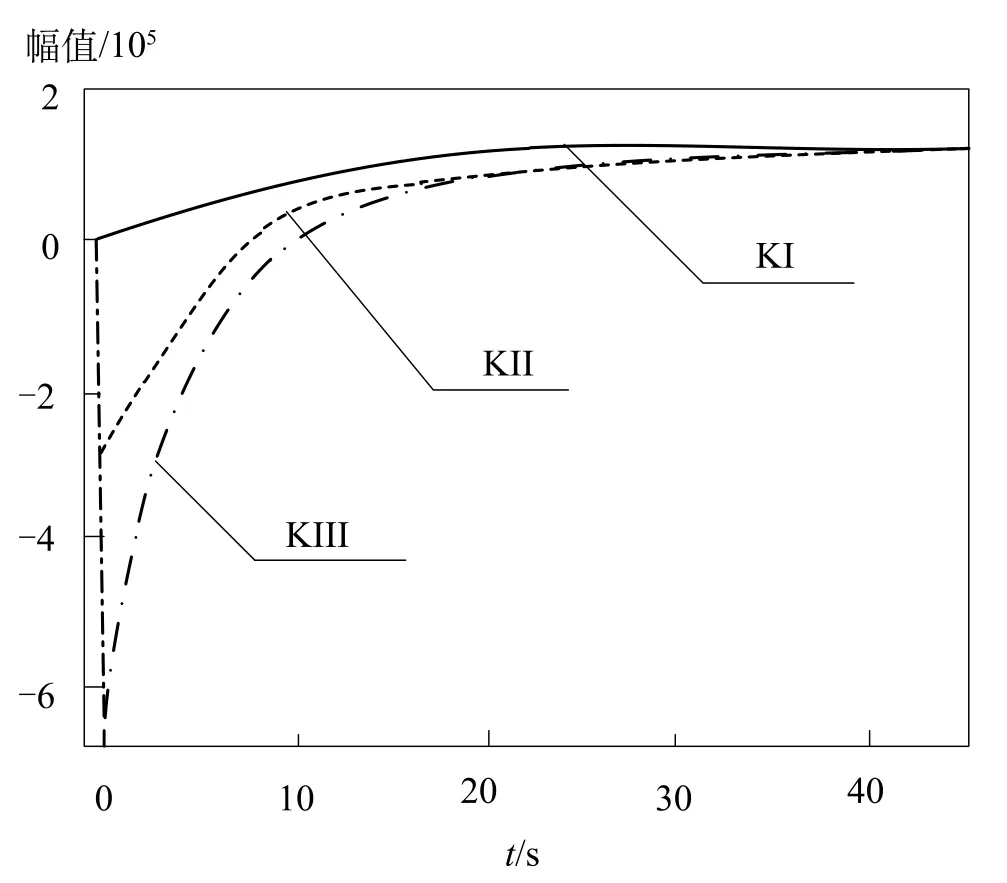
圖1 不同增益數值條件下的階躍響應曲線圖

1.3 最大功率點實時檢測與跟蹤

通過上述論述可知，在光伏發電系統運行過程中，光照強度與電池溫度和光伏電池的輸出功率之間存在非線性的關系，因此在對其最大功率點進行檢測時，本文引入SVR算法，通過該算法克服傳統機器學習算法在運算過程中存在的問題，實現對最大功率點的檢測。將SVR算法輸入計算機當中，得到光伏發電系統電池輸出電壓隨時間變化的數值，如下表所示。

表 光伏發電系統電池輸出電壓記錄表

通過上表的光伏發電系統電池輸出電壓變化數據可以看出，隨著運行時間的增加，其輸出電壓呈現出緩慢下降的趨勢，在0.20～0.30s時間范圍內出現了輕微的上浮，但總體電壓變化趨勢并不明顯。同時，在這一過程中對光照強度進行檢測，在0.05～0.1s時，光照強度和溫度是恒定不變的；在0.10～0.15s時，光照強度出現逐漸減弱的現象，而溫度仍然保持著恒定不變的狀態；在0.15～0.20s時，光照強度呈現出逐漸減弱的趨勢，而溫度也隨之出現不斷降低的趨勢；在0.20～0.25s時，光照強度始終保持恒定不變，而溫度出現明顯降低趨勢。綜合上述變化趨勢，對光伏發電系統的最大功率點進行檢測，采用網格搜索法，通過對搜索參數范圍以內劃分的網格結構進行搜索，找出在該范圍內最優的參數。在搜索前需要將歷史電壓數據作為依據，對歷史最大功率點電壓數據進行歸一化處理，其表達式為：

式（5）中，x*表示歸一化處理后的電壓數據；xmin表示為最小電壓數據；xmax表示為最大電壓數據；x表示為電壓數據集合中的任意一個數值結果。按照上述公式計算，完成對電壓數據的歸一化處理后，還需要結合高斯RBF核函數實現對網格搜索的訓練，其公式為：

式（6）中，k（x，y）表示網格結構中的某一坐標點；－g表示核函數參數。完成對網絡搜索的訓練后，為了找出最精確的最大功率點，將搜索的范圍設定在光伏發電系統電池輸出電壓變化幅度較大的區域范圍內，并將初始的搜索步長設置為10，采用交叉驗證的方法對被搜索范圍內的所有功率點進行測試［5］。再調整步長大小，將尋優結果的搜尋范圍逐漸縮小，最終在最小的范圍內確定最優參數，該數值結尾最大功率點所在位置，以此實現對最大功率點的檢測與跟蹤。

2 對比實驗

完成對基于階躍響應的光伏發電最大功率點檢測方法理論研究后，為了進一步驗證該方法在實際應用中的優勢，選擇某電力企業的光伏發電系統作為實驗對象，根據光伏發電原理，通過Matlab平臺設計一個雙饋異步光電循環發電機組，并進行下述實驗驗證。實驗過程中，選擇將傳統檢測方法作為對照組，將本文提出的基于階躍響應的檢測方法作為實驗組，將兩種檢測方法同時應用到上述雙饋異步光電循環發電機組當中，針對光伏發電系統在運行過程中的最大功率點進行檢測。人為在光伏發電系統當中設置10～80個不等的最大功率點，利用兩種檢測方法完成對其最大功率點的檢測后，將結果進行記錄，并將其與設定的實際最大功率點電壓進行對比，得到如圖2所示的實驗結果。

從圖2得出的實驗結果可以看出，實驗組與對照組相比明顯更加接近實際值最大功率點電壓的變化曲線。在實驗過程中，在最大功率點個數為30～45個范圍內，對照組曲線與實際值曲線相差較大的主要原因是，在這一段檢測時間當中，由于受到了雷雨天氣的影響，使得光伏發電系統當中的電池溫度和光照強度都發生了明顯的變化，對照組的檢測方法受到了較大影響，而實驗組的檢測方法能夠結合階躍響應實現對上述問題出現時對光伏發電情況的準確預測，因此得到的檢測結果精度更高。通過上述實驗及得出的實驗結果進一步說明，本文提出的基于階躍響應的光伏發電最大功率點檢測方法在實際應用中能夠保證檢測結果與實際相符，有效提高檢測精度，為光伏發電系統的穩定運行提供數據條件。

圖2 實驗組與對照組實驗結果對比圖

3 結束語

為實現對光伏發電最大功率點的高精度檢測，在明確光伏發電原理的基礎上，結合階躍響應提出一種全新的檢測方法，并結合實驗證明了該方法與其他檢測方法相比存在的優勢。隨著數字處理器性能的不斷提高，本文還將數字處理器應用到對光伏發電最大功率點檢測方法當中，從而進一步提高檢測方法的有效性和實時性，促進光伏發電系統運行效率的提升。